Erreur absolue moyenne expliquée : Mesure de la précision du modèle

Vous avez donc exécuté un modèle et vous devez maintenant l'évaluer. Choisir la bonne métrique peut s'avérer compliqué, car il existe plusieurs options telles que MAE, MSE, RMSE, etc. 

Toutes ces mesures évaluent les erreurs, mais elles fournissent des informations légèrement différentes sur les performances de votre modèle. Dans cet article, nous allons nous intéresser à l'un des plus courants que vous devez connaître en tant que data scientist : l'erreur absolue moyenne (MAE). Comme vous le constaterez, MAE offre une vision claire de la précision des prévisions sans compliquer les choses.

Qu'est-ce que l'erreur absolue moyenne (MAE) ?

Lorsque vous avez besoin d'un moyen clair pour mesurer la précision de vos prévisions, l'erreur absolue moyenne est un bon point de départ. Il vous indique, en moyenne, l'écart entre les prévisions de votre modèle et les valeurs réelles, sans vous soucier de savoir si ces prévisions étaient trop élevées ou trop basses.

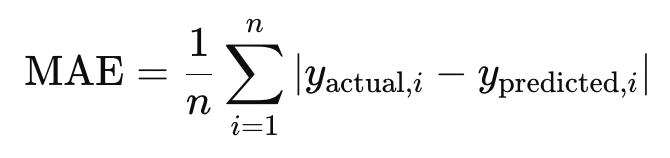
Dans cette équation, n représente le nombre total de prédictions. La valeur absolue, que vous pouvez voir avec les barres verticales, garantit que toutes les erreurs sont considérées comme positives, de sorte que les surestimations et les sous-estimations ont le même poids. Il s'agit d'une mesure simple et directe de l'erreur de prédiction moyenne de votre modèle, ce qui explique pourquoi elle est si souvent utilisée.

Pourquoi devriez-vous vous intéresser au MAE ?

J'ai déjà commencé à évoquer tout cela : Le MAE est particulièrement utile car il est facile à comprendre. Si votre MAE est égal à 5, cela signifie que les prédictions de votre modèle présentent un écart moyen de 5 unités.

Pour comprendre cela, il est nécessaire de se référer à la notion d'erreur quadratique moyenne, ou MSE, qui a pour effet de donner plus de poids aux erreurs importantes en les élevant au carré. Avec MSE, les valeurs aberrantes peuvent fausser considérablement votre évaluation.

Comment calculez-vous la MAE ? (Avec exemple Python)

Examinons un exemple rapide à l'aide de Python. Supposons que vous ayez élaboré un modèle pour prédire les ventes mensuelles et que vous souhaitiez maintenant vérifier sa précision. Voici comment calculer la MAE :

import numpy as np

actual = np.array([100, 150, 200, 250])
predicted = np.array([110, 140, 210, 240])

mae = np.mean(np.abs(actual - predicted))
print("MAE:", mae)

MAE: 10.0

Ce code calcule la différence absolue entre chaque valeur réelle et prédite, puis en calcule la moyenne. Le résultat (10,0 ici) correspond à la taille typique de l'erreur de prédiction.

Où est utilisé le MAE ?

Les détaillants utilisent souvent le MAE pour vérifier dans quelle mesure leurs prévisions correspondent aux ventes réelles. Il s'agit d'un cas d'utilisation très courant. Une MAE élevée peut indiquer que le modèle doit être réentraîné ou ajusté. Je pourrais également imaginer que, dans le domaine de la santé, la MAE permette de mesurer la précision des délais de rétablissement prévus par rapport aux résultats réels. Une MAE plus faible renforce la confiance dans la capacité du modèle à produire des estimations utiles.

Ce ne sont là que quelques exemples, mais l'analyse MAE peut être utilisée dans toutes les situations où vous comparez des valeurs numériques prévisionnelles et réelles. Les possibilités sont trop nombreuses pour être énumérées.

Comment le MAE se compare-t-il à d'autres indicateurs ?

Le MAE n'est pas le seul moyen d'évaluer l'erreur de prédiction. Selon le type d'erreurs qui vous préoccupe le plus, d'autres indicateurs pourraient être plus appropriés.

MAE contre MSE

Le MSE examine également la différence entre les valeurs prévues et les valeurs réelles, mais il élève chaque erreur au carré avant de calculer la moyenne. Cela le rend plus sensible aux erreurs importantes. Si les erreurs importantes ont plus d'importance dans votre cas d'utilisation, MSE pourrait être plus adapté.

MAE contre RMSE

La RMSE est la racine carrée de la MSE. Il replace l'erreur dans les unités d'origine, ce qui facilite son interprétation par rapport à l'erreur quadratique moyenne. Cependant, tout comme MSE, il accorde davantage d'importance aux erreurs importantes.

Si vous souhaitez traiter toutes les erreurs de la même manière et simplifier les choses, MAE est un choix judicieux. Toutefois, si vous êtes davantage préoccupé par l'impact des erreurs importantes, la MSE ou la RMSE pourraient être plus appropriées.

Conclusion

Le MAE est un moyen clair et pratique de mesurer l'écart entre vos prévisions et les valeurs réelles. Il est facile à calculer, simple à expliquer et utile dans un large éventail d'applications.

Bien qu'il ne mette pas en évidence les erreurs importantes comme le font le MSE ou le RMSE, il donne une image fidèle de la précision globale. Utilisez-le lorsque vous souhaitez obtenir une mesure directe qui n'est pas trop influencée par quelques erreurs importantes.

Cela étant dit, il est recommandé d'utiliser le MAE en complément d'autres indicateurs, en particulier lorsque vous comparez des modèles ou affinez les performances. Veuillez consulter pour obtenir plus d'informations sur le MAE et d'autres indicateurs de performance. Au fil du temps, vous saurez déterminer quand le MAE est suffisant et quand l', un autre indicateur, fournit davantage d'informations. Suivez notre cours Comprendre la science des données et notre cours Introduction à la régression avec statsmodels en Python pour développer vos compétences et votre intuition.