RMSE expliqué : Un guide sur la précision de la prédiction de régression

L'erreur quadratique moyenne (RMSE) est une mesure d'évaluation de la précision couramment utilisée dans l'analyse de régression, qui mesure l'ampleur moyenne des erreurs dans un modèle de régression.

Contrairement au R au carré, qui quantifie la variance expliquée, le RMSE fournit une mesure directe de l'erreur de prédiction dans les mêmes unités que la variable réponse. Il est donc particulièrement utile lorsque l'objectif est de minimiser l'ampleur des erreurs et d'interpréter les performances du modèle en termes réels.

Dans cet article, nous examinerons la signification, le calcul, l'interprétation et les idées fausses les plus courantes concernant le RMSE. Nous parcourrons également des exemples en Python et en R pour voir comment se comporte le RMSE dans différentes conditions de modélisation.

Qu'est-ce que le RMSE ?

La RMSE est la racine carrée de la moyenne des différences quadratiques entre les valeurs observées et les valeurs prédites. Il s'agit d'une mesure de régression largement utilisée qui nous indique le degré d'erreur à attendre de nos prédictions, en moyenne. 

La formule mathématique pour calculer le RMSE est la suivante :

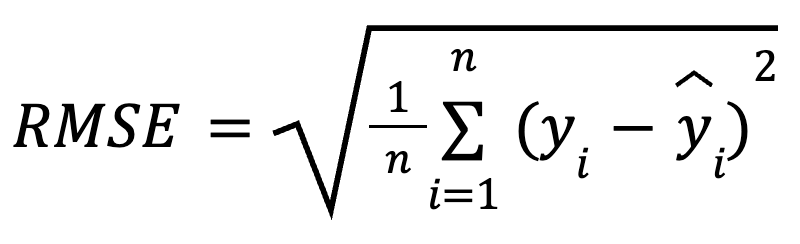
ici :

• y_i est la valeur réelle de l'observation i,
• _ŷ, est la valeur prédite pour l'observation i,
• n est le nombre total d'observations.

En élevant les résidus au carré avant de calculer la moyenne, le RMSE pénalise plus fortement les erreurs importantes que les petites. Cette sensibilité en fait un bon choix lorsque des erreurs de prédiction importantes sont particulièrement indésirables. Le RMSE est toujours non négatif, et des valeurs plus faibles indiquent un meilleur ajustement du modèle.

Trois façons égales de calculer l'erreur quadratique moyenne (RMSE)

Le RMSE est facile à calculer. Il s'agit simplement de calculer les résidus, de les élever au carré, de trouver la moyenne et de prendre la racine carrée.

Examinons quelques manières différentes de la calculer.

Utilisation des résidus

Dans cette méthode, nous commençons par soustraire les prédictions des valeurs réelles pour obtenir les résidus. Ensuite, nous élevons chaque résidu au carré, nous en faisons la moyenne et enfin nous prenons la racine carrée.

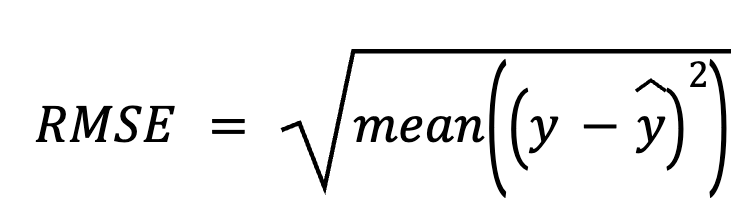
ici :

• y est le vecteur des valeurs réelles,
• ŷest le vecteur des valeurs prédites.

Cette approche directe met l'accent sur les erreurs de prédiction elles-mêmes.

Utilisation de l'erreur quadratique moyenne (EQM)

Celle-ci ressemble à une redite, mais il y a plus que cela : La RMSE est simplement la racine carrée de la MSE. 

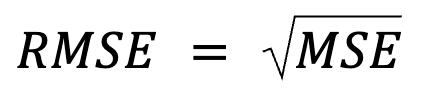
où :

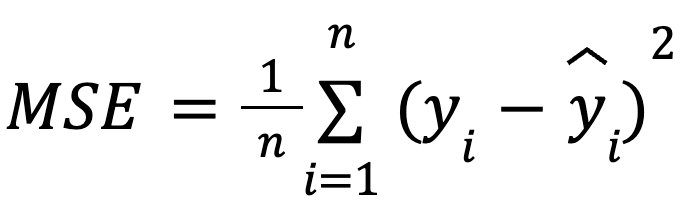
avec :

• y_i la valeur réelle de l'observation i,
• ŷ, comme valeur prédite pour l'observation i,
• n le nombre total d'observations.

Cette formulation est utile car l'EQM est une fonction de perte courante dans l'optimisation des modèles. Cette équivalence est particulièrement importante dans l'apprentissage automatique, où l'EQM est souvent la fonction de perte minimisée lors de l'apprentissage par descente de gradient. 

Plus d'informations à ce sujet : C'est précisément parce que le RMSE introduit une racine carrée que de nombreux algorithmes d'apprentissage automatique choisissent de ne pas utiliser le RMSE lors de l'apprentissage du modèle. L'EQM est préférée pour ces optimisations parce qu'elle a des dérivées plus simples (encore une fois, parce que la racine carrée introduit une non-linéarité). La RMSE est alors souvent utilisée après coup pour rendre compte de la performance en unités interprétables.

Sous forme de matrice

Dans le cadre d'une régression multiple, la RMSE peut également être dérivée du vecteur résiduel à l'aide de l'algèbre matricielle :

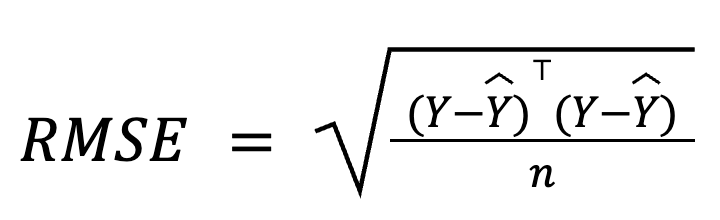
où :

• Y est le vecteur colonne des valeurs réelles,
• ŷ est le vecteur colonne des valeurs prédites,
• n est le nombre d'observations.

Cette formulation basée sur une matrice est particulièrement compacte et efficace sur le plan informatique, notamment pour les grands ensembles de données ou les pipelines de modèles. Si vous souhaitez étudier les mathématiques, nous proposons un cours d'algèbre linéaire.

Interprétation de la RMSE

Le RMSE est interprété comme l'erreur moyenne de prédiction, qui détermine la précision de prédiction du modèle. En d'autres termes, elle montre, en moyenne, à quel point les prédictions sont éloignées des valeurs réelles, dans la même échelle que la variable de résultat.

Un RMSE plus faible indique des erreurs de prédiction moyennes plus petites et, par conséquent, des prédictions plus précises, mais le RMSE "acceptable" dépend entièrement du contexte. Par exemple, un RMSE de 2 peut être bon pour prédire la taille des amandes en millimètres, mais pas si convaincant pour prédire les rendements annuels des cultures d'amandes en tonnes.

Pour être significative, la RMSE doit être comparée entre des modèles formés sur les mêmes données ou par le biais d'une analyse comparative des performances historiques.

Quand utiliser le RMSE

Le RMSE est particulièrement utile dans ces scénarios :

• Quand la précision absolue de la prédiction est essentielle
• Lorsque vous comparez des modèles sur le même ensemble de données
• Lorsque les erreurs du modèlesont normalement distribuées
• Lorsque notre objectif est de minimiser les erreurs importantes
• Lorsqu'il est important d'interpréter les erreurs dans les unités naturelles

Cependant, le RMSE présente des inconvénients :

• Il est sensible aux valeurs aberrantes. Quelques résidus importants peuvent affecter de manière disproportionnée le RMSE et le rendre trompeur.
• Elle n'est pas normalisée. Cela signifie qu'il n'est pas possible d'effectuer des comparaisons entre différents ensembles de données et échelles cibles, à moins que la variable cible ne soit mise à l'échelle.

Exemples de RMSE en Python et R

Illustrons maintenant comment calculer le RMSE à la fois en Python et en R en utilisant le jeu de données Kaggle Classification des types d'amandes. Bien que l'ensemble de données soit à l'origine destiné à la classification, nous le réutiliserons ici pour la régression en prédisant l'épaisseur du noyau en tant que variable continue basée sur d'autres attributs physiques.

Nous construirons deux modèles dans chaque langage de programmation et nous calculerons le RMSE pour chaque modèle :

• Modèle 1 : Utilise des prédicteurs pertinents (longueur et largeur).
• Modèle 2 : Ajoute un prédicteur aléatoire et non pertinent.

Exemple en Python

Commençons par Python.

import pandas as pd
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
from math import sqrt

# Load data
data = pd.read_csv("almond_dataset.csv")

# Model 1
X1 = data[['Length', 'Width']]
y = data['Thickness']
model1 = LinearRegression().fit(X1, y)
preds1 = model1.predict(X1)
rmse1 = sqrt(mean_squared_error(y, preds1))
print("Model 1 RMSE:", round(rmse1, 3))

# Model 2 with an irrelevant predictor
np.random.seed(42)
data['random_noise'] = np.random.randn(len(data))
X2 = data[['Length', 'Width', 'random_noise']]
model2 = LinearRegression().fit(X2, y)
preds2 = model2.predict(X2)
rmse2 = sqrt(mean_squared_error(y, preds2))
print("Model 2 RMSE:", round(rmse2, 3))

Model 1 RMSE: 0.251
Model 2 RMSE: 0.253

Nous pouvons constater que le RMSE a augmenté après l'ajout d'un prédicteur non pertinent dans le modèle 2. Bien que le modèle 2 puisse sembler plus complexe, sa précision de prédiction réelle peut se dégrader (et de manière significative !) puisque nous venons d'ajouter un bruit aléatoire.

Pour améliorer vos compétences en matière de régression en Python, inscrivez-vous à ces cours :

• Introduction à la régression avec statsmodels en Python
• Régression intermédiaire avec statsmodels en Python

Exemple R

Essayons maintenant avec R.

# Load data
almonds <- read.csv("almond_dataset.csv")

# Model 1
model1 <- lm(Thickness ~ Length + Width, data = almonds)
preds1 <- predict(model1)
rmse1 <- sqrt(mean((almonds$Thickness - preds1)^2))
print(paste("Model 1 RMSE:", round(rmse1, 3)))

# Model 2 with an irrelevant predictor
set.seed(42)
almonds$random_noise <- rnorm(nrow(almonds))
model2 <- lm(Thickness ~ Length + Width + random_noise, data = almonds)
preds2 <- predict(model2)
rmse2 <- sqrt(mean((almonds$Thickness - preds2)^2))
print(paste("Model 2 RMSE:", round(rmse2, 3)))

[1] "Model 1 RMSE: 0.251"
[1] "Model 2 RMSE: 0.253"

Ici, j'ai remodelé le même exemple en R. La RMSE augmente lorsque nous incluons un prédicteur non pertinent en R. Cela confirme que la RMSE peut augmenter lorsqu'un modèle devient inutilement complexe, réduisant ainsi la capacité de généralisation du modèle.

Si vous avez eu des difficultés à compiler votre code R ou à interpréter le résultat, essayez nos cours :

• Introduction à la régression en R
• Régression intermédiaire en R

RMSE vs. Mesures connexes

Le RMSE fait partie d'une famille plus large de mesures d'erreur de régression. Comparons-le brièvement à d'autres, clarifions les différences entre eux et soulignons quand chacun est le plus utile.

RMSE vs. MAE

Le RMSE pénalise plus lourdement les erreurs importantes car il élève les résidus au carré, ce qui le rend plus sensible aux valeurs aberrantes. La MAE (erreur absolue moyenne), en revanche, est plus résistante aux valeurs aberrantes, traite toutes les erreurs de la même manière et fonctionne mieux pour mesurer la taille d'une erreur typique lorsque les valeurs aberrantes ne posent pas de problème. Alors que le RMSE minimise la perte au carré, le MAE minimise la perte absolue.

En général, nous devrions utiliser le RMSE lorsque des erreurs importantes peuvent être particulièrement coûteuses, et le MAE lorsque nous voulons une vision médiane de l'erreur, moins sensible aux valeurs aberrantes.

RMSE vs. R au carré

Le RMSE fournit l'erreur moyenne en unités originales, ce qui le rend plus intuitifpour une interprétation pratique. Le R au carré décrit plutôt la variance expliquée par le modèle, mais n'indique pas la taille de l'erreur de prédiction.

Ils sont souvent utilisés ensemble : R-carré pour l'ajustement relatif et RMSE pour la performance absolue.

RMSE vs. MSE

La RMSE est simplement la racine carrée de la MSE, ce qui la rend plus facile à interpréter car elle est exprimée dans les mêmes unités que la variable de résultat. 

Au-delà de la simple interprétation, MSE est particulièrement utile pour l'optimisation de la formation dans le cadre de l'apprentissage automatique. Rappelez-vous que si vous optimisez sur le RMSE, la fonction racine carrée signifie que le modèle met davantage l'accent sur les erreurs les plus importantes. En outre, l'EQM a une dérivée lisse et fonctionne donc bien avec les algorithmes basés sur le gradient, comme la descente de gradient stochastique, ce qui permet une convergence efficace lors de l'apprentissage du modèle. En bref, le RMSE est plus facile à interpréter car nous examinons les résultats à l'échelle des données, mais nous devons savoir que l'apprentissage profond optimise souvent le MSE, et non le RMSE.

RMSE vs. MAPE

MAPE (mean absolute percentage error) renvoie les erreurs en pourcentage, ce qui est pratique pour comparer des ensembles de données. Cependant, il s'effondre lorsque les valeurs réelles sont proches de zéro, ce qui le rend instable. Le RMSE évite ce problème et est plus fiable en présence de petites valeurs cibles.

RMSE vs. log-vraisemblance

Voici une autre relation intéressante : La RMSE est formellement équivalente à la log-vraisemblance négative dans le cas d'erreurs gaussiennes. Nous devrions plutôt dire que minimiser la RMSE équivaut à maximiser la log-vraisemblance (d'un modèle de régression) dans l'hypothèse d'erreurs normalement distribuées (avec une variance constante). Je ne dis pas que la RMSE estime à elle seule la log-vraisemblance complète, mais je dis que la minimisation de laRMSE maximise implicitement la log-vraisemblance sous l'hypothèse d'une erreur normale.

Toutefois, lorsque les erreurs sont asymétriques ou présentent des valeurs aberrantes, des solutions alternatives telles que la perte de Huber ou la perte de quantile peuvent donner de meilleurs résultats. En tout état de cause, nous devons considérer le choix de la métrique comme une décision de conception du modèle, et non comme une réflexion a posteriori.

Idées reçues sur le RMSE

Clarifions quelques mythes répandus sur le RMSE :

• "Un faible RMSE garantit une bonne généralisation du modèle. Ce n'est pas nécessairement vrai. Un modèle peut avoir une faible valeur de RMSE sur les données d'apprentissage, mais donner des résultats médiocres sur de nouvelles données inédites en raison d'un surajustement. Pour évaluer efficacement la généralisation, nous devons procéder à une validation croisée ou utiliser un ensemble de tests distinct.
• "Le RMSE permet de déterminer si un modèle est surajusté. Le RMSE seul ne suffit pas. Elle doit être comparée entre les ensembles de données d'entraînement et de validation : si la RMSE d'entraînement est faible mais que la RMSE de validation est beaucoup plus élevée, cela me signifie un surajustement.
• "Il existe un seuil universel fixe pour un bon RMSE. Non, il n'y en a pas. La question de savoir si la valeur de la RMSE est "bonne" dépend entièrement du contexte, du domaine et des unités de la variable de résultat. En d'autres termes, les valeurs RMSE ne sont pas significatives en l'absence de contexte.

Conclusion

En résumé, le RMSE est une mesure pratique, interprétable et intuitive de la précision de la prédiction qui communique l'erreur moyenne de prédiction dans les unités de la variable cible. Il s'agit d'une mesure de référence pour l'évaluation des performances de régression, en particulier lorsque l'ampleur des erreurs est importante.

Cependant, le RMSE doit être utilisé avec d'autres mesures telles que le R au carré, le MAE et les scores de validation croisée afin d'obtenir une image plus complète de la qualité du modèle. Il ne faut pas se fier aveuglément à cette mesure, mais toujours tenir compte de l'échelle, du contexte et de la complexité du modèle. En outre, l'association du RMSE à des diagnostics visuels peut aider à détecter les biais. 

En bref, le RMSE nous indique à quel point notre modèle est erroné, en moyenne, en termes réels, ce qui constitue une perspective importante à conserver lors de l'élaboration de systèmes prédictifs.

Si cet article vous a paru confus, ne vous inquiétez pas : Nous disposons de nombreuses ressources pour vous aider : 

• Régression linéaire simple : Tout ce que vous devez savoir tutoriel
• Comprendre la somme des carrés : Un guide pour les tutoriels SST, SSR et SSE
• Cours d'introduction à la régression avec statsmodels en Python
• Introduction à la régression en R