Exponentes em Python: Um guia abrangente para iniciantes

A exponenciação é fundamental em várias áreas de programação, desde a análise de dados até o design de algoritmos. Suas aplicações incluem a análise de padrões exponenciais em grandes conjuntos de dados, como tendências de mídia social, e a realização de cálculos matemáticos, como crescimento composto ou taxas de juros.

Além disso, a exponenciação desempenha um papel fundamental no aprendizado de máquina (ML) e na inteligência artificial (IA), especialmente em redes neurais e reconhecimento de imagens. Portanto, é essencial que você saiba como realizar cálculos com expoentes de forma eficaz em Python.

Neste guia, exploraremos vários métodos para realizar a exponenciação em Python. Examinaremos as funções incorporadas, as funções do módulo math e as da biblioteca Numpy. Cada método tem suas vantagens.

Além disso, vamos nos aprofundar em um cenário prático para que você tenha uma compreensão mais clara dos usos da exponenciação.

Exponentes em Python

O Python oferece várias maneiras de calcular expoentes:

• **: O operador de asterisco duplo (**) é a opção mais simples e básica para a exponenciação. Por exemplo, x ** y calcula x elevado à potência de y.
• pow(): Essa função incorporada recebe dois argumentos: a base e o expoente. Ele retorna o resultado do aumento da base para o expoente. Ele também permite um terceiro argumento opcional para exponenciação modular. Exemplo: pow(x, y).
• math.pow(): Essa função do módulo math é semelhante à pow(), mas sempre retorna um resultado de ponto flutuante. Ele recebe dois argumentos, que podem ser floats ou inteiros. Exemplo: math.pow(x, y).
• math.exp(): Outra função do módulo math, que retorna o exponencial natural de um número, ou seja, e elevado à potência do argumento. Exemplo: math.exp(argument).
• np.power(): Essa função da biblioteca NumPy foi projetada para que você trabalhe com matrizes ou vetores. Ele executa a exponenciação por elementos. Exemplo: np.power(array, exponent).

Noções básicas de expoente em Python

O operador de asterisco duplo (**) é a maneira mais direta do Python de calcular a exponenciação. Esse operador eleva o operando da esquerda (base) à potência do operando da direita (expoente). Ele também é chamado de operador de potência ou operador de expoente.

Se você deseja aprimorar suas habilidades de programação em Python e aprender a programar como um verdadeiro programador, confira o curso Programação em Python.

Expoente positivo

Neste trecho de código, mostramos como calcular a exponenciação usando expoentes positivos. Por exemplo, 2 elevado à potência de 3 é calculado como 2 × 2 × 2, resultando em 8. Da mesma forma, -10 elevado à potência de 4 é calculado como -10 × -10 × -10 × -10, resultando em 10000.

base = 2
exponent = 3
print(base**exponent)  # Output: 8

base = -10
exponent = 4
print(base**exponent)  # Output: 10000

Expoente negativo

Esse código calcula o resultado de elevar uma base a um expoente negativo. Por exemplo, 5 elevado à potência de -2 é igual a 0,04. Da mesma forma, 25 elevado à potência de -5 resulta em um valor muito pequeno representado em notação científica (1,024e-07).

base = 5
exponent = -2
print(base**exponent) # 0.04

base = 25
exponent = -5
print(base**exponent) # 1.024e-07

Elevar um número a um expoente negativo é equivalente a tomar o recíproco do número elevado ao expoente positivo.

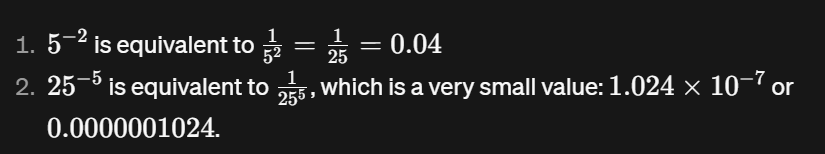
Em Python, o operador ** retorna um ZeroDivisionError se você elevar 0,0 a uma potência negativa, pois qualquer número dividido por zero é indefinido.

base = 0
exponent = -5
print(base**exponent)

O resultado é:

Expoente de ponto flutuante

Os exemplos de código mostram que o Python calcula corretamente o resultado de elevar uma base positiva como 2 a um expoente fracionário como 1,5. Entretanto, o uso de uma base negativa com um expoente fracionário resulta em um número complexo.

base = 2
exponent = 1.5
print(base**exponent) # 2.8284271247461903

base = -0.25
exponent = 1.25
print(base**exponent) # (-0.12500000000000003-0.125j)

Mergulhando mais fundo: Funções incorporadas

O Python oferece várias funções internas para calcular expoentes, mas vamos nos concentrar em duas: pow() e math.pow(). À primeira vista, essas funções podem parecer semelhantes, mas elas têm algumas diferenças significativas. Vamos nos aprofundar em cada função em detalhes.

pow()

A função pow() recebe dois argumentos obrigatórios: base e expoente. Opcionalmente, pow() aceita um terceiro argumento opcional para calcular o módulo do valor exponencial. A sintaxe é a seguinte: pow(base, exp, mod), em que 'mod' representa o módulo. Essa função retorna o restante da exponenciação.

Exponenciação básica

Para cálculos básicos, basta fornecer a base e o expoente à função, que funciona de forma semelhante ao operador **.

r = pow(2, 3)
print(r) # 8

r = pow(4, -10)
print(r) # 2.56e-06

Exponenciação de ponto flutuante

No código abaixo, estamos usando números de ponto flutuante para bases e expoentes, alguns dos quais são negativos. Essa abordagem funciona de forma semelhante à do operador **.

r = pow(3.5, 2)
print(r)  # 12.25

r = pow(3.5, -2)
print(r)  # 0.08163265306122448

r = pow(3.5, 3.2)
print(r)  # 55.08301986166747

r = pow(-3.5, -3.3)
print(r)  # (-0.009414432347757688+0.012957854474952653j)

r = pow(-3.5, 3.3)
print(r)  # (-36.698070584660925-50.510560868902246j)

Observação: Se você estiver lidando com exponenciação básica sem precisar de cálculos modulares, o operador ** é uma solução mais concisa e legível em comparação com a função pow().

Exponenciação modular

O parâmetro opcional modulus da função pow() é muito útil quando você trabalha com exponenciação modular. Isso é particularmente útil em criptografia ou ao lidar com números grandes, pois a exponenciação modular oferece maior eficiência. Por exemplo, ao calcular 3 elevado à potência de 4 no módulo 5, o resultado é 1, pois 81 no módulo 5 é igual a 1.

r = pow(3, 4, 5)
print(r)  # 1

r = pow(123, 456, 789)
print(r)  # 699

r = pow(2, -3, 7)
print(r)  # 1

r = pow(-13, 8, 62)
print(r)  # 7

Você pode se perguntar por que usar pow() diretamente para a exponenciação modular é mais eficiente do que pow(base, exp) % mod ou (base**exp) % mod. A função incorporada pow() foi projetada especificamente para essa operação, enquanto os outros métodos realizam cálculos intermediários desnecessários. Isso pode fazer uma diferença significativa no desempenho, especialmente com valores grandes.

import timeit

start_pow_mod = timeit.default_timer()
pow(500000000, 3000, 4000)
stop_pow_mod = timeit.default_timer()

pow_mod_time = stop_pow_mod - start_pow_mod

print("Time using pow(base, exp, mod): ", pow_mod_time)

start_pow_other = timeit.default_timer()
pow(500000000, 3000) % 4000
stop_pow_other = timeit.default_timer()

pow_other_time = stop_pow_other - start_pow_other

print("Time using pow(base, exp) % mod:", pow_other_time)


start_aestrisk = timeit.default_timer()
(500000000**3000) % 4000
stop_aestrisk = timeit.default_timer()

aestrisk_time = stop_aestrisk - start_aestrisk

print("Time using (base ** exp) % mod: ", aestrisk_time)


print(
    f"Speed comparison: pow(base, exp, mod) was {pow_other_time / pow_mod_time} times faster than pow(base, exp) % mod and {aestrisk_time/pow_mod_time} times faster than (base ** exp) % mod"
)

O resultado é:

A função pow() pode gerar erros diferentes, dependendo da situação.

# Trying to take the modulo of complex numbers raises a ValueError.
print(pow(2 + 3j, 4, 5))  # ValueError: complex modulo

# Taking the third argument is not allowed if the second argument is negative.
print(pow(10, -11, 4))  # ValueError: base is not invertible for the given modulus

# If the first or second argument is a float, the third argument is not allowed.
print(pow(2.4, 3, 4))  # TypeError: pow() 3rd argument not allowed unless all arguments are integers

# Passing any argument as a string results in a TypeError.
print(pow(2, 4, '3'))  # TypeError: unsupported operand type(s) for pow(): 'int', 'int', 'str'

math.pow()

A função math.pow(x, n) eleva x à potência de n. O math.pow() converte os argumentos em pontos flutuantes e retorna o resultado como uma exponenciação precisa de ponto flutuante. Essa precisão é crucial em campos como análise de dados e computação científica, em que a precisão é fundamental.

Aqui está o código simples. A função math.pow() retorna um valor de ponto flutuante, enquanto a função pow() retorna um valor inteiro.

import math
print(math.pow(6, 3))  # 216.0
print(pow(6, 3))  # 216

A função math.pow() não aceita números imaginários.

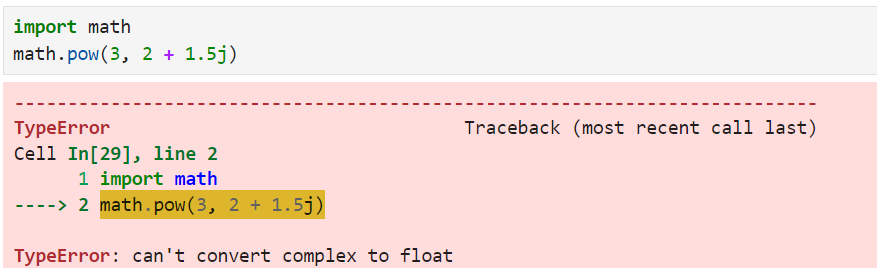
O site math.pow() não aceita bases negativas com expoentes fracionários, pois isso gerará um ValueError.

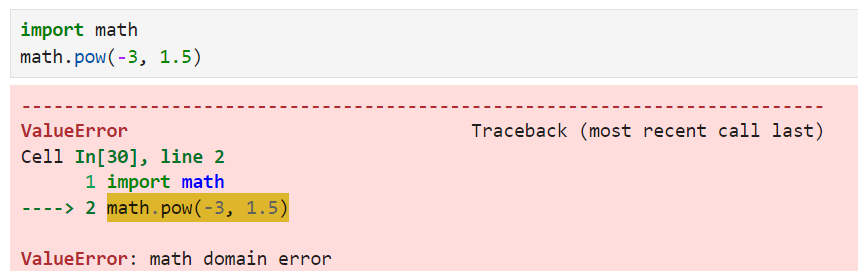
Aproveitamento de bibliotecas para exponenciação avançada

Para lidar com tarefas avançadas de exponenciação, como encontrar o valor exponencial de um número ou calcular a exponenciação de elementos em matrizes, você pode usar duas funções: np.power() e math.exp().

np.power()

No Python, a exponenciação não se limita às funções incorporadas. O Python tem uma biblioteca poderosa chamada NumPy, que permite uma ampla variedade de operações matemáticas em matrizes. Às vezes, você precisa lidar com a exponenciação em matrizes inteiras, e é aí que entra o np.power(). Ele foi projetado para exponenciação de matrizes com elementos.

import numpy as np
r = np.power([2, 4, 8], 2)
print(r)  # [4, 16, 64]

r = np.power([2, 4, 8], [1, 2, 3])
print(r)  # [4 64 4096]

r = np.power([[2, 3, 4], [5, 6, 7]], [1, 2, 3])
print(r) # [[2 9 64] [5 36 343]]

A função np.power() não aceita um expoente negativo.

import numpy as np
r = np.power([2, 4, 8], -2)
print(r)

O resultado é:

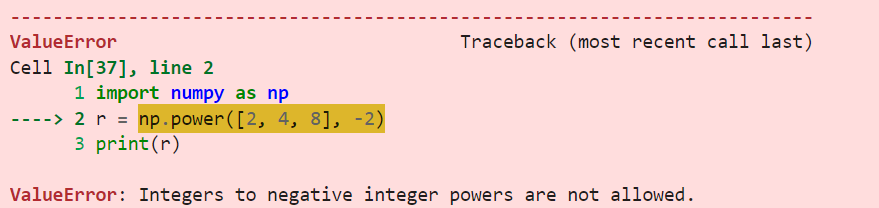
Se você tentar elevar um número negativo a uma potência não inteira, o NumPy retornará um valor NaN (Not a Number).

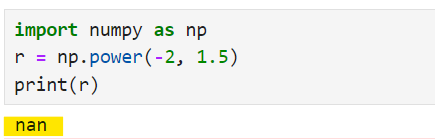
math.exp()

A função math.exp(x) calcula o valor exponencial de x, o que equivale a elevar o número de Euler e à potência de x. O número de Euler é aproximadamente igual a 2,71828 e, na notação matemática, essa operação é representada por e^x.

import math
x = 2
r = math.exp(x)
print("Exponential of", x, ":", r) # 7.38905609893065

Uma característica importante do math.exp(x) é sua adaptabilidade. Ele pode lidar com números positivos, negativos e até mesmo com números de ponto flutuante.

import math
print(math.exp(-2))  # 0.1353352832366127
print(math.exp(-2.5))  # 0.0820849986238988
print(math.exp(2.5))  # 12.182493960703473

Aplicações práticas e exemplos

A exponenciação é uma operação fundamental da matemática com inúmeras aplicações em análise de dados e computação científica.

Se você quiser dominar os fundamentos da análise de dados com Python, confira o curso Introduction to Python for Data Science.

Digamos que você tenha um arquivo CSV contendo dados sobre o valor principal, a taxa de juros e o período de investimento para várias linhas. Você pode calcular os juros compostos para cada linha usando qualquer um dos métodos discutidos acima.

Principal,Rate,Years
1000,0.05,5
2000,0.03,10
1500,0.08,3
3000,0.06,7
2500,0.04,9
1800,0.07,4
2200,0.025,6
3500,0.09,2
2800,0.035,8
4000,0.02,5

Aqui está o código:

import csv


def compound_interest(principal, rate, years):
    return principal * (1 + rate) ** years


# Read data from CSV file

data = []
with open("data.csv", newline="") as csvfile:
    reader = csv.DictReader(csvfile)
    for row in reader:
        row["Compound Interest"] = compound_interest(
            float(row["Principal"]), float(row["Rate"]), int(row["Years"])
        )
        data.append(row)
# Write data to a new CSV file with compound interest column

output_file = "data.csv"
fieldnames = ["Principal", "Rate", "Years", "Compound Interest"]

with open(output_file, mode="w", newline="") as csvfile:
    writer = csv.DictWriter(csvfile, fieldnames=fieldnames)
    writer.writeheader()
    for row in data:
        writer.writerow(row)
print("Compound interest calculations saved to", output_file)

O resultado é:

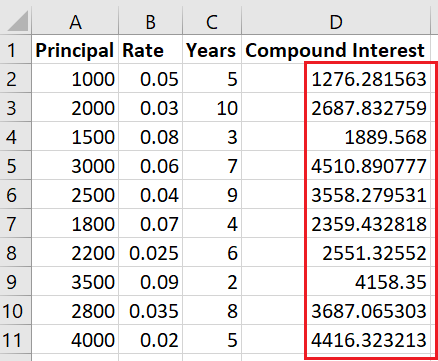
Ótimo! Você calculou os juros compostos para todas as linhas e os armazenou em uma coluna separada. Você pode usar esses dados para análises adicionais. Da mesma forma, há centenas de outros casos de uso em que a exponenciação é usada extensivamente, como a modelagem do crescimento populacional ao longo do tempo.

Conclusão

Neste guia, exploramos cinco métodos diferentes para calcular expoentes em Python, cada um oferecendo vantagens exclusivas. Você pode usá-los em muitos cenários práticos, como encontrar juros compostos, modelar o crescimento populacional e muito mais.

Operador de asterisco duplo (**): Simples e direto para o uso diário.

pow(): Versátil com um truque opcional de "módulo".

math.pow(): Resultados precisos como números de ponto flutuante.

np.power(): Poderoso para lidar com matrizes com verificação de erros.

math.exp(): Ferramenta dedicada para calcular o valor exponencial.

Se você quiser aumentar suas habilidades estatísticas e aprender a coletar, analisar e tirar conclusões precisas dos dados usando Python, confira o curso Introdução à estatística em Python.