Cursus
L'exponentiation est fondamentale dans divers domaines de programmation, de l'analyse des données à la conception d'algorithmes. Ses applications comprennent l'analyse de modèles exponentiels dans de grands ensembles de données tels que les tendances des médias sociaux et l'exécution de calculs mathématiques tels que la croissance composée ou les taux d'intérêt.
En outre, l'exponentiation joue un rôle crucial dans l'apprentissage automatique (ML) et l'intelligence artificielle (IA), en particulier dans les réseaux neuronaux et la reconnaissance d'images. Il est donc essentiel de comprendre comment effectuer efficacement des calculs avec des exposants en Python.
Dans ce guide, nous allons explorer différentes méthodes pour effectuer l'exponentiation en Python. Nous examinerons les fonctions intégrées, les fonctions du module mathématique et celles de la bibliothèque Numpy. Chaque méthode a ses avantages.
En outre, nous nous pencherons sur un scénario pratique pour mieux comprendre l'utilisation de l'exponentiation.
Les exposants en Python
Python offre plusieurs façons de calculer les exposants :
- **: L'opérateur double astérisque (**) est l'option la plus simple et la plus élémentaire pour l'exponentiation. Par exemple,
x ** ycalculexélevé à la puissance dey. - pow(): Cette fonction intégrée prend deux arguments : la base et l'exposant. Il renvoie le résultat de l'élévation de la base à l'exposant. Il autorise également un troisième argument facultatif pour l'exponentiation modulaire. Exemple :
pow(x, y). - math.pow(): Cette fonction du module
mathest similaire àpow(), mais elle renvoie toujours un résultat en virgule flottante. Elle prend deux arguments, qui peuvent tous deux être des nombres entiers ou flottants. Exemple :math.pow(x, y). - math.exp(): Autre fonction du module
math, elle renvoie l'exponentielle naturelle d'un nombre, c'est-à-direeélevée à la puissance de l'argument. Exemple :math.exp(argument). - np.power(): Cette fonction de la bibliothèque NumPy est conçue pour travailler avec des tableaux ou des matrices. Il effectue une exponentiation par élément. Exemple :
np.power(array, exponent).
Les bases de l'exposant en Python
L'opérateur double astérisque (**) est le moyen le plus simple de calculer l'exponentiation en Python. Cet opérateur élève l'opérande de gauche (base) à la puissance de l'opérande de droite (exposant). Il est également appelé opérateur de puissance ou opérateur d'exposant.
Si vous souhaitez améliorer vos compétences en programmation Python et apprendre à coder comme un vrai programmeur, consultez le cours Python Programming.
Exposant positif
Dans cet extrait de code, nous montrons comment calculer l'exponentiation à l'aide d'exposants positifs. Par exemple, 2 élevé à la puissance 3 est calculé comme 2 × 2 × 2, ce qui donne 8. De même, -10 élevé à la puissance 4 est calculé comme -10 × -10 × -10 × -10, ce qui donne 10000.
base = 2
exponent = 3
print(base**exponent) # Output: 8
base = -10
exponent = 4
print(base**exponent) # Output: 10000Exposant négatif
Ce code calcule le résultat de l'élévation d'une base à un exposant négatif. Par exemple, 5 élevé à la puissance -2 est égal à 0,04. De même, 25 élevé à la puissance -5 donne une très petite valeur représentée en notation scientifique (1,024e-07).
base = 5
exponent = -2
print(base**exponent) # 0.04
base = 25
exponent = -5
print(base**exponent) # 1.024e-07Élever un nombre à un exposant négatif revient à prendre la réciproque du nombre élevé à l'exposant positif.
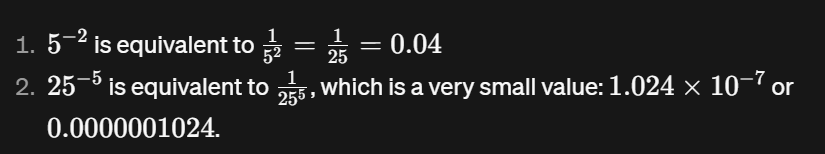
En Python, l'opérateur ** renvoie une ZeroDivisionError si vous élevez 0,0 à une puissance négative, car tout nombre divisé par zéro est indéfini.
base = 0
exponent = -5
print(base**exponent)Le résultat est le suivant :

Exposant en virgule flottante
Les exemples de code montrent que Python calcule correctement le résultat de l'élévation d'une base positive comme 2 à un exposant fractionnaire comme 1,5. Cependant, l'utilisation d'une base négative avec un exposant fractionnaire donne un nombre complexe.
base = 2
exponent = 1.5
print(base**exponent) # 2.8284271247461903
base = -0.25
exponent = 1.25
print(base**exponent) # (-0.12500000000000003-0.125j)Plongée en profondeur : Fonctions intégrées
Python propose plusieurs fonctions intégrées pour calculer les exposants, mais nous nous concentrerons sur deux d'entre elles : pow() et math.pow(). À première vue, ces fonctions peuvent sembler similaires, mais elles présentent des différences significatives. Examinons chaque fonction en détail.
pow()
La fonction pow() prend deux arguments obligatoires : la base et l'exposant. En option, pow() accepte un troisième argument facultatif pour calculer le module de la valeur exponentielle. La syntaxe est la suivante : pow(base, exp, mod), où "mod" représente le module. Cette fonction renvoie le reste de l'exponentiation.
Exponentiation de base
Pour les calculs de base, il suffit d'indiquer la base et l'exposant à la fonction, qui fonctionne de la même manière que l'opérateur **.
r = pow(2, 3)
print(r) # 8
r = pow(4, -10)
print(r) # 2.56e-06Exponentiation en virgule flottante
Dans le code ci-dessous, nous utilisons des nombres à virgule flottante pour les bases et les exposants, dont certains sont négatifs. Cette approche fonctionne de la même manière que l'opérateur **.
r = pow(3.5, 2)
print(r) # 12.25
r = pow(3.5, -2)
print(r) # 0.08163265306122448
r = pow(3.5, 3.2)
print(r) # 55.08301986166747
r = pow(-3.5, -3.3)
print(r) # (-0.009414432347757688+0.012957854474952653j)
r = pow(-3.5, 3.3)
print(r) # (-36.698070584660925-50.510560868902246j)Note : Si vous avez affaire à une exponentiation de base sans avoir besoin de calculs modulaires, l'opérateur ** est une solution plus concise et plus lisible que la fonction pow().
Exponentiation modulaire
Le paramètre optionnel modulus de la fonction pow() est très utile pour travailler avec l'exponentiation modulaire. Ceci est particulièrement utile en cryptographie ou pour traiter de grands nombres, car l'exponentiation modulaire offre une meilleure efficacité. Par exemple, lorsque l'on calcule 3 élevé à la puissance 4 modulo 5, le résultat est 1, puisque 81 modulo 5 est égal à 1.
r = pow(3, 4, 5)
print(r) # 1
r = pow(123, 456, 789)
print(r) # 699
r = pow(2, -3, 7)
print(r) # 1
r = pow(-13, 8, 62)
print(r) # 7Vous vous demandez peut-être pourquoi l'utilisation directe de pow() pour l'exponentiation modulaire est plus efficace que pow(base, exp) % mod ou (base**exp) % mod. La fonction intégrée pow() est spécialement conçue pour cette opération, alors que les autres méthodes effectuent des calculs intermédiaires inutiles. Cela peut faire une différence significative en termes de performances, en particulier avec des valeurs élevées.
import timeit
start_pow_mod = timeit.default_timer()
pow(500000000, 3000, 4000)
stop_pow_mod = timeit.default_timer()
pow_mod_time = stop_pow_mod - start_pow_mod
print("Time using pow(base, exp, mod): ", pow_mod_time)
start_pow_other = timeit.default_timer()
pow(500000000, 3000) % 4000
stop_pow_other = timeit.default_timer()
pow_other_time = stop_pow_other - start_pow_other
print("Time using pow(base, exp) % mod:", pow_other_time)
start_aestrisk = timeit.default_timer()
(500000000**3000) % 4000
stop_aestrisk = timeit.default_timer()
aestrisk_time = stop_aestrisk - start_aestrisk
print("Time using (base ** exp) % mod: ", aestrisk_time)
print(
f"Speed comparison: pow(base, exp, mod) was {pow_other_time / pow_mod_time} times faster than pow(base, exp) % mod and {aestrisk_time/pow_mod_time} times faster than (base ** exp) % mod"
)Le résultat est le suivant :

La fonction pow() peut générer différentes erreurs en fonction de la situation.
# Trying to take the modulo of complex numbers raises a ValueError.
print(pow(2 + 3j, 4, 5)) # ValueError: complex modulo
# Taking the third argument is not allowed if the second argument is negative.
print(pow(10, -11, 4)) # ValueError: base is not invertible for the given modulus
# If the first or second argument is a float, the third argument is not allowed.
print(pow(2.4, 3, 4)) # TypeError: pow() 3rd argument not allowed unless all arguments are integers
# Passing any argument as a string results in a TypeError.
print(pow(2, 4, '3')) # TypeError: unsupported operand type(s) for pow(): 'int', 'int', 'str'math.pow()
La fonction math.pow(x, n) élève x à la puissance n. Le site math.pow() convertit les arguments en nombres flottants et renvoie le résultat sous la forme d'une exponentiation précise en virgule flottante. Cette précision devient cruciale dans des domaines tels que l'analyse de données et le calcul scientifique, où la précision est primordiale.
Voici le code simple. La fonction math.pow() renvoie une valeur en virgule flottante, tandis que la fonction pow() renvoie une valeur entière.
import math
print(math.pow(6, 3)) # 216.0
print(pow(6, 3)) # 216La fonction math.pow() n'accepte pas les nombres imaginaires.
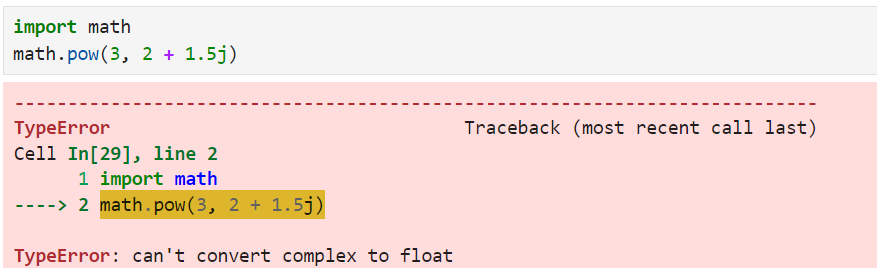
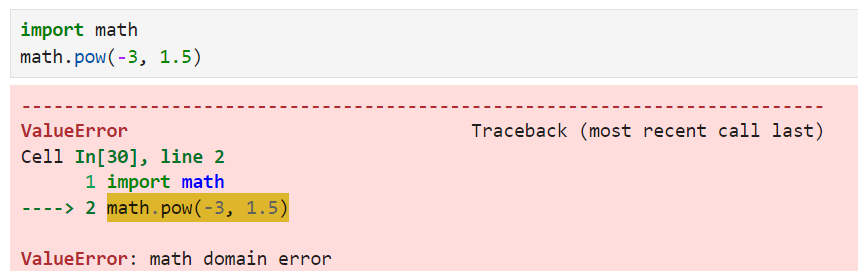
Le site math.pow() n'accepte pas les bases négatives avec des exposants fractionnaires car il soulèvera un ValueError.
Exploiter les bibliothèques pour une exponentiation avancée
Pour effectuer des tâches d'exponentiation avancées, telles que la recherche de la valeur exponentielle d'un nombre ou le calcul de l'exponentiation par élément dans des tableaux ou des matrices, vous pouvez vous appuyer sur deux fonctions : np.power() et math.exp().
np.power()
En Python, l'exponentiation n'est pas limitée aux fonctions intégrées. Python dispose d'une puissante bibliothèque appelée NumPy, qui permet d'effectuer une grande variété d'opérations mathématiques sur les tableaux. Parfois, vous devez gérer l'exponentiation sur des tableaux entiers, et c'est là que np.power() entre en jeu. Il est conçu pour l'exponentiation par éléments de tableaux.
import numpy as np
r = np.power([2, 4, 8], 2)
print(r) # [4, 16, 64]
r = np.power([2, 4, 8], [1, 2, 3])
print(r) # [4 64 4096]
r = np.power([[2, 3, 4], [5, 6, 7]], [1, 2, 3])
print(r) # [[2 9 64] [5 36 343]]La fonction np.power() n'accepte pas d'exposant négatif.
import numpy as np
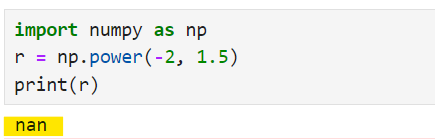
r = np.power([2, 4, 8], -2)
print(r)Le résultat est le suivant :
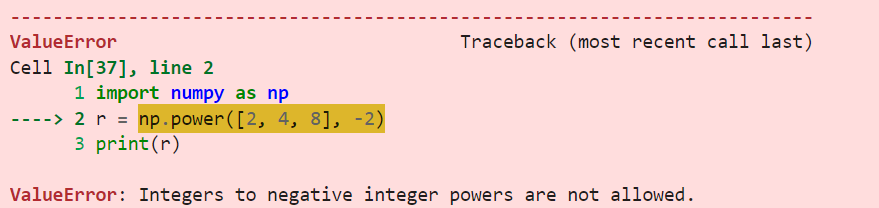
Si vous tentez d'élever un nombre négatif à une puissance non entière, NumPy renvoie une valeur NaN (Not a Number).
math.exp()
La fonction math.exp(x) calcule la valeur exponentielle de x, ce qui équivaut à élever le nombre d'Euler e à la puissance de x. Le nombre d'Euler est approximativement égal à 2,71828, et en notation mathématique, cette opération est représentée par e^x.
import math
x = 2
r = math.exp(x)
print("Exponential of", x, ":", r) # 7.38905609893065L'une des principales caractéristiques de math.exp(x) est son adaptabilité. Il peut traiter des nombres positifs, des nombres négatifs et même des nombres à virgule flottante.
import math
print(math.exp(-2)) # 0.1353352832366127
print(math.exp(-2.5)) # 0.0820849986238988
print(math.exp(2.5)) # 12.182493960703473Applications pratiques et exemples
L'exponentiation est une opération fondamentale en mathématiques qui trouve de nombreuses applications dans l'analyse des données et le calcul scientifique.
Si vous souhaitez maîtriser les bases de l'analyse de données avec Python, consultez le cours Introduction à Python pour la science des données.
Supposons que vous disposiez d'un fichier CSV contenant des données sur le montant du capital, le taux d'intérêt et la période d'investissement pour plusieurs lignes. Vous pouvez calculer les intérêts composés pour chaque ligne en utilisant l'une des méthodes décrites ci-dessus.
Principal,Rate,Years
1000,0.05,5
2000,0.03,10
1500,0.08,3
3000,0.06,7
2500,0.04,9
1800,0.07,4
2200,0.025,6
3500,0.09,2
2800,0.035,8
4000,0.02,5Voici le code :
import csv
def compound_interest(principal, rate, years):
return principal * (1 + rate) ** years
# Read data from CSV file
data = []
with open("data.csv", newline="") as csvfile:
reader = csv.DictReader(csvfile)
for row in reader:
row["Compound Interest"] = compound_interest(
float(row["Principal"]), float(row["Rate"]), int(row["Years"])
)
data.append(row)
# Write data to a new CSV file with compound interest column
output_file = "data.csv"
fieldnames = ["Principal", "Rate", "Years", "Compound Interest"]
with open(output_file, mode="w", newline="") as csvfile:
writer = csv.DictWriter(csvfile, fieldnames=fieldnames)
writer.writeheader()
for row in data:
writer.writerow(row)
print("Compound interest calculations saved to", output_file)Le résultat est le suivant :
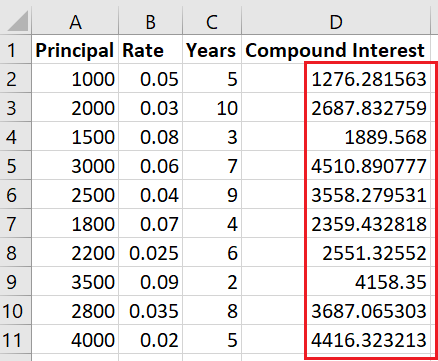
Excellent ! Vous avez calculé les intérêts composés pour toutes les lignes et les avez stockés dans une colonne distincte. Vous pouvez utiliser ces données pour une analyse plus approfondie. De même, il existe des centaines d'autres cas d'utilisation où l'exponentiation est largement utilisée, comme la modélisation de la croissance de la population au fil du temps.
Conclusion
Dans ce guide, nous avons exploré cinq méthodes différentes pour calculer les exposants en Python, chacune offrant des avantages uniques. Vous pouvez les utiliser pour de nombreux scénarios pratiques, tels que la recherche d'intérêts composés, la modélisation de la croissance démographique, etc.
Opérateur à double astérisque (**) : Simple et direct pour un usage quotidien.
pow() : Polyvalent grâce à l'option "modulus".
math.pow() : Résultats précis sous forme de nombres à virgule flottante.
np.power(): Puissant pour manipuler des tableaux avec contrôle d'erreur.
math.exp() : Outil dédié au calcul de la valeur exponentielle.
Si vous souhaitez développer vos compétences statistiques et apprendre à collecter, analyser et tirer des conclusions précises à partir de données en utilisant Python, consultez le cours Introduction aux statistiques en Python.
