Exponenten in Python: Ein umfassender Leitfaden für Anfänger

Die Potenzierung ist in verschiedenen Bereichen der Programmierung von grundlegender Bedeutung, von der Datenanalyse bis zum Entwurf von Algorithmen. Zu seinen Anwendungen gehören die Analyse exponentieller Muster in großen Datensätzen wie Trends in sozialen Medien und die Durchführung mathematischer Berechnungen wie Zinseszins oder Zinseszinsen.

Außerdem spielt die Potenzierung eine wichtige Rolle beim maschinellen Lernen (ML) und der künstlichen Intelligenz (KI), insbesondere bei neuronalen Netzen und der Bilderkennung. Deshalb ist es wichtig zu verstehen, wie man in Python effektiv mit Exponenten rechnet.

In diesem Leitfaden werden wir verschiedene Methoden zur Durchführung der Potenzierung in Python kennenlernen. Wir werden integrierte Funktionen, Funktionen aus dem Mathematikmodul und Funktionen aus der Numpy-Bibliothek untersuchen. Jede Methode hat ihre Vorteile.

Außerdem werden wir uns mit einem praktischen Szenario beschäftigen, um ein besseres Verständnis für die Anwendung der Potenzierung zu bekommen.

Exponenten in Python

Python bietet mehrere Möglichkeiten, Exponenten zu berechnen:

• **: Der Doppel-Sternchen-Operator (**) ist die einfachste und grundlegendste Option für die Potenzierung. Zum Beispiel berechnet x ** y die Potenz x von y.
• pow(): Diese eingebaute Funktion benötigt zwei Argumente: die Basis und den Exponenten. Sie gibt das Ergebnis der Erhöhung der Basis auf den Exponenten zurück. Sie erlaubt auch ein optionales drittes Argument für die modulare Potenzierung. Beispiel: pow(x, y).
• math.pow(): Diese Funktion aus dem Modul math ist ähnlich wie pow(), liefert aber immer ein Fließkomma-Ergebnis. Sie benötigt zwei Argumente, die beide Fließkommazahlen oder ganze Zahlen sein können. Beispiel: math.pow(x, y).
• math.exp(): Eine weitere Funktion aus dem Modul math, die den natürlichen Exponentialwert einer Zahl zurückgibt, d.h. e hochgezählt mit dem Argument. Beispiel: math.exp(argument).
• np.power(): Diese Funktion aus der NumPy-Bibliothek ist für die Arbeit mit Arrays oder Matrizen gedacht. Sie führt eine elementweise Potenzierung durch. Beispiel: np.power(array, exponent).

Grundlagen des Python-Exponenten

Der Doppel-Sternchen-Operator (**) ist Pythons einfachste Art, die Potenzierung zu berechnen. Dieser Operator erhöht den linken Operanden (Basis) mit der Potenz des rechten Operanden (Exponent). Er wird auch Potenzoperator oder Exponentenoperator genannt.

Wenn du deine Python-Programmierkenntnisse verbessern und lernen willst, wie ein echter Programmierer zu programmieren, dann schau dir den Kurs Python Programming an.

Positiver Exponent

In diesem Codeschnipsel zeigen wir, wie man die Potenzierung mit positiven Exponenten berechnet. Zum Beispiel wird 2 hoch 3 als 2 × 2 × 2 berechnet, was 8 ergibt. Ähnlich wird -10 hoch 4 als -10 × -10 × -10 × -10 × -10 berechnet, was 10000 ergibt.

base = 2
exponent = 3
print(base**exponent)  # Output: 8

base = -10
exponent = 4
print(base**exponent)  # Output: 10000

Negativer Exponent

Dieser Code berechnet das Ergebnis der Erhöhung einer Basis auf einen negativen Exponenten. Zum Beispiel ist 5 hoch -2 gleich 0,04. Ebenso ergibt 25 hoch -5 einen sehr kleinen Wert in wissenschaftlicher Notation (1,024e-07).

base = 5
exponent = -2
print(base**exponent) # 0.04

base = 25
exponent = -5
print(base**exponent) # 1.024e-07

Das Erhöhen einer Zahl mit negativem Exponenten ist gleichbedeutend mit dem Kehrwert der Zahl, die mit dem positiven Exponenten erhöht wurde.

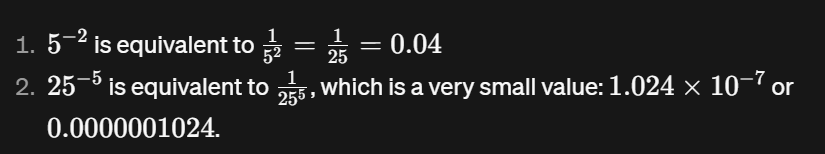
In Python gibt der **-Operator einen ZeroDivisionError zurück, wenn du 0,0 auf eine negative Potenz erhöhst, weil jede durch Null geteilte Zahl undefiniert ist.

base = 0
exponent = -5
print(base**exponent)

Die Ausgabe ist:

Fließkomma-Exponent

Die Codebeispiele zeigen, dass Python das Ergebnis korrekt berechnet, wenn man eine positive Basis wie 2 auf einen gebrochenen Exponenten wie 1,5 erhöht. Die Verwendung einer negativen Basis mit einem gebrochenen Exponenten ergibt jedoch eine komplexe Zahl.

base = 2
exponent = 1.5
print(base**exponent) # 2.8284271247461903

base = -0.25
exponent = 1.25
print(base**exponent) # (-0.12500000000000003-0.125j)

Tiefer eintauchen: Eingebaute Funktionen

Python bietet verschiedene eingebaute Funktionen zur Berechnung von Exponenten, aber wir werden uns auf zwei konzentrieren: pow() und math.pow(). Auf den ersten Blick mögen diese Funktionen ähnlich erscheinen, aber es gibt einige wichtige Unterschiede. Schauen wir uns jede Funktion im Detail an.

pow()

Die Funktion pow() benötigt zwei obligatorische Argumente: Basis und Exponent. Optional akzeptiert pow() ein drittes Argument, um den Modulus des Exponentialwerts zu berechnen. Die Syntax lautet wie folgt: pow(base, exp, mod), wobei "mod" für den Modulus steht. Diese Funktion gibt den Rest der Potenzierung zurück.

Grundlegende Potenzierung

Für grundlegende Berechnungen gibst du der Funktion einfach die Basis und den Exponenten an, die ähnlich wie der Operator ** funktioniert.

r = pow(2, 3)
print(r) # 8

r = pow(4, -10)
print(r) # 2.56e-06

Fließkomma-Potenzierung

Im folgenden Code verwenden wir Fließkommazahlen sowohl für die Basen als auch für die Exponenten, von denen einige negativ sind. Dieser Ansatz funktioniert ähnlich wie der ** Operator.

r = pow(3.5, 2)
print(r)  # 12.25

r = pow(3.5, -2)
print(r)  # 0.08163265306122448

r = pow(3.5, 3.2)
print(r)  # 55.08301986166747

r = pow(-3.5, -3.3)
print(r)  # (-0.009414432347757688+0.012957854474952653j)

r = pow(-3.5, 3.3)
print(r)  # (-36.698070584660925-50.510560868902246j)

Hinweis: Wenn es um einfache Potenzierung geht, ohne dass modulare Berechnungen erforderlich sind, ist der ** Operator eine prägnantere und lesbarere Lösung als die pow() Funktion.

Modulare Potenzierung

Der optionale Modulus-Parameter der Funktion pow() ist bei der Arbeit mit der modularen Potenzierung sehr nützlich. Dies ist vor allem in der Kryptografie oder beim Umgang mit großen Zahlen nützlich, da die modulare Potenzierung eine bessere Effizienz bietet. Wenn du zum Beispiel 3 hoch 4 modulo 5 berechnest, ist das Ergebnis 1, da 81 modulo 5 gleich 1 ist.

r = pow(3, 4, 5)
print(r)  # 1

r = pow(123, 456, 789)
print(r)  # 699

r = pow(2, -3, 7)
print(r)  # 1

r = pow(-13, 8, 62)
print(r)  # 7

Du fragst dich vielleicht, warum die direkte Verwendung von pow() für die modulare Potenzierung effizienter ist als pow(base, exp) % mod oder (base**exp) % mod. Die eingebaute Funktion pow() ist speziell für diesen Vorgang gedacht, während die anderen Methoden unnötige Zwischenberechnungen durchführen. Das kann einen erheblichen Unterschied in der Leistung ausmachen, besonders bei großen Werten.

import timeit

start_pow_mod = timeit.default_timer()
pow(500000000, 3000, 4000)
stop_pow_mod = timeit.default_timer()

pow_mod_time = stop_pow_mod - start_pow_mod

print("Time using pow(base, exp, mod): ", pow_mod_time)

start_pow_other = timeit.default_timer()
pow(500000000, 3000) % 4000
stop_pow_other = timeit.default_timer()

pow_other_time = stop_pow_other - start_pow_other

print("Time using pow(base, exp) % mod:", pow_other_time)


start_aestrisk = timeit.default_timer()
(500000000**3000) % 4000
stop_aestrisk = timeit.default_timer()

aestrisk_time = stop_aestrisk - start_aestrisk

print("Time using (base ** exp) % mod: ", aestrisk_time)


print(
    f"Speed comparison: pow(base, exp, mod) was {pow_other_time / pow_mod_time} times faster than pow(base, exp) % mod and {aestrisk_time/pow_mod_time} times faster than (base ** exp) % mod"
)

Die Ausgabe ist:

Die Funktion pow() kann je nach Situation verschiedene Fehler auslösen.

# Trying to take the modulo of complex numbers raises a ValueError.
print(pow(2 + 3j, 4, 5))  # ValueError: complex modulo

# Taking the third argument is not allowed if the second argument is negative.
print(pow(10, -11, 4))  # ValueError: base is not invertible for the given modulus

# If the first or second argument is a float, the third argument is not allowed.
print(pow(2.4, 3, 4))  # TypeError: pow() 3rd argument not allowed unless all arguments are integers

# Passing any argument as a string results in a TypeError.
print(pow(2, 4, '3'))  # TypeError: unsupported operand type(s) for pow(): 'int', 'int', 'str'

math.pow()

Die Funktion math.pow(x, n) erhebt x in die Potenz von n. Die math.pow() wandelt die Argumente in Fließkommazahlen um und gibt das Ergebnis als präzise Fließkomma-Exponentierung zurück. Diese Präzision ist besonders wichtig in Bereichen wie der Datenanalyse und dem wissenschaftlichen Rechnen, wo es auf Genauigkeit ankommt.

Hier ist der einfache Code. Die Funktion math.pow() gibt einen Fließkommawert zurück, während die Funktion pow() einen Ganzzahlwert zurückgibt.

import math
print(math.pow(6, 3))  # 216.0
print(pow(6, 3))  # 216

Die Funktion math.pow() akzeptiert keine imaginären Zahlen.

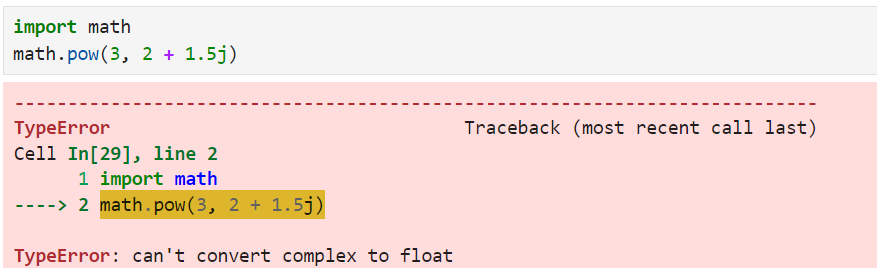
Die math.pow() akzeptiert keine negativen Basen mit gebrochenen Exponenten, da sie eine ValueError aufruft.

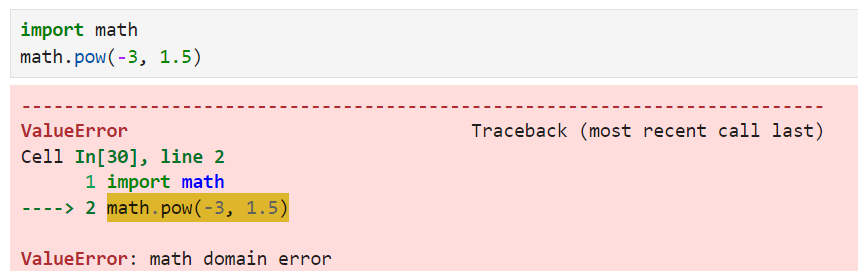
Nutzung von Bibliotheken für erweiterte Potenzierung

Für fortgeschrittene Potenzierungsaufgaben, wie z.B. das Ermitteln des Exponentialwertes einer Zahl oder das Berechnen der elementweisen Potenzierung in Arrays oder Matrizen, kannst du zwei Funktionen nutzen: np.power() und math.exp().

np.power()

In Python ist die Potenzierung nicht auf die eingebauten Funktionen beschränkt. Python hat eine leistungsstarke Bibliothek namens NumPy, die eine Vielzahl von mathematischen Operationen auf Arrays ermöglicht. Manchmal musst du die Potenzierung über ganze Arrays hinweg handhaben, und hier kommt np.power() ins Spiel. Sie ist für die elementweise Potenzierung von Arrays gedacht.

import numpy as np
r = np.power([2, 4, 8], 2)
print(r)  # [4, 16, 64]

r = np.power([2, 4, 8], [1, 2, 3])
print(r)  # [4 64 4096]

r = np.power([[2, 3, 4], [5, 6, 7]], [1, 2, 3])
print(r) # [[2 9 64] [5 36 343]]

Die Funktion np.power() akzeptiert keinen negativen Exponenten.

import numpy as np
r = np.power([2, 4, 8], -2)
print(r)

Die Ausgabe ist:

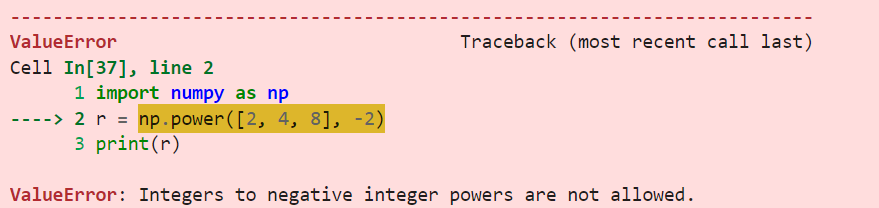
Wenn du versuchst, eine negative Zahl auf eine nicht-ganzzahlige Potenz zu erhöhen, gibt NumPy einen NaN (Not a Number) Wert zurück.

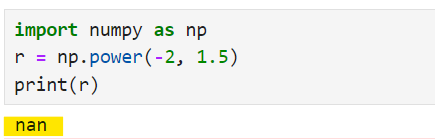
math.exp()

Die Funktion math.exp(x) berechnet den Exponentialwert von x, was einer Potenzierung der Eulerschen Zahl e mit x entspricht. Die Eulersche Zahl ist ungefähr gleich 2,71828, und in der mathematischen Notation wird diese Operation als e^x dargestellt.

import math
x = 2
r = math.exp(x)
print("Exponential of", x, ":", r) # 7.38905609893065

Ein wichtiges Merkmal von math.exp(x) ist seine Anpassungsfähigkeit. Sie kann mit positiven und negativen Zahlen und sogar mit Gleitkommazahlen umgehen.

import math
print(math.exp(-2))  # 0.1353352832366127
print(math.exp(-2.5))  # 0.0820849986238988
print(math.exp(2.5))  # 12.182493960703473

Praktische Anwendungen und Beispiele

Die Potenzierung ist eine grundlegende Operation in der Mathematik mit zahlreichen Anwendungen in der Datenanalyse und im wissenschaftlichen Rechnen.

Wenn du die Grundlagen der Datenanalyse mit Python beherrschen willst, schau dir den Kurs Einführung in Python für Data Science an.

Angenommen, du hast eine CSV-Datei mit Daten zu Kapitalbetrag, Zinssatz und Investitionszeitraum für mehrere Zeilen. Du kannst die Zinseszinsen für jede Zeile mit einer der oben beschriebenen Methoden berechnen.

Principal,Rate,Years
1000,0.05,5
2000,0.03,10
1500,0.08,3
3000,0.06,7
2500,0.04,9
1800,0.07,4
2200,0.025,6
3500,0.09,2
2800,0.035,8
4000,0.02,5

Hier ist der Code:

import csv


def compound_interest(principal, rate, years):
    return principal * (1 + rate) ** years


# Read data from CSV file

data = []
with open("data.csv", newline="") as csvfile:
    reader = csv.DictReader(csvfile)
    for row in reader:
        row["Compound Interest"] = compound_interest(
            float(row["Principal"]), float(row["Rate"]), int(row["Years"])
        )
        data.append(row)
# Write data to a new CSV file with compound interest column

output_file = "data.csv"
fieldnames = ["Principal", "Rate", "Years", "Compound Interest"]

with open(output_file, mode="w", newline="") as csvfile:
    writer = csv.DictWriter(csvfile, fieldnames=fieldnames)
    writer.writeheader()
    for row in data:
        writer.writerow(row)
print("Compound interest calculations saved to", output_file)

Das Ergebnis ist:

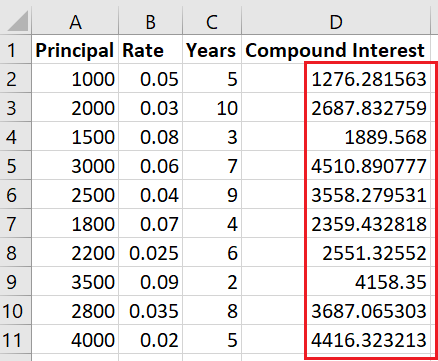
Toll! Du hast den Zinseszins für alle Zeilen berechnet und in einer separaten Spalte gespeichert. Du kannst diese Daten für weitere Analysen nutzen. Ebenso gibt es Hunderte von anderen Anwendungsfällen, in denen die Potenzierung ausgiebig genutzt wird, z. B. bei der Modellierung des Bevölkerungswachstums über die Zeit.

Fazit

In diesem Leitfaden haben wir fünf verschiedene Methoden zur Berechnung von Exponenten in Python untersucht, die jeweils einzigartige Vorteile bieten. Du kannst sie für viele praktische Szenarien nutzen, z. B. um den Zinseszins zu berechnen, das Bevölkerungswachstum zu modellieren und vieles mehr.

Doppelasterisk-Operator (**): Einfach und direkt für den täglichen Gebrauch.

pow(): Vielseitig mit einem optionalen "Modulus"-Trick.

math.pow(): Präzise Ergebnisse als Gleitkommazahlen.

np.power(): Leistungsstark für den Umgang mit Arrays mit Fehlerprüfung.

math.exp(): Spezielles Tool zur Berechnung des Exponentialwerts.

Wenn du deine statistischen Fähigkeiten ausbauen und lernen willst, wie du mit Python Daten sammelst, analysierst und genaue Schlussfolgerungen aus ihnen ziehst, solltest du dir den Kurs Einführung in die Statistik in Python ansehen.