Dominando a retropropagação: Um guia abrangente para redes neurais

A retropropagação é uma parte essencial do treinamento de redes neurais modernas, permitindo que esses algoritmos sofisticados aprendam com conjuntos de dados de treinamento e melhorem com o tempo.

Compreender e dominar o algoritmo de retropropagação é fundamental para qualquer pessoa no campo das redes neurais e da aprendizagem profunda. Este tutorial oferece uma exploração aprofundada da retropropagação.

Ele começa explicando o que é a retropropagação e como ela funciona, além de suas vantagens e limitações, antes de mergulhar em uma experiência prática de aplicação em um conjunto de dados amplamente utilizado.

O que é backpropagation?

Introduzido na década de 1970, o algoritmo de retropropagação é o método de ajuste fino dos pesos de uma rede neural em relação à taxa de erro obtida na iteração ou época anterior, e é um método padrão de treinamento de redes neurais artificiais.

Você pode pensar nisso como um sistema de feedback em que, após cada rodada de treinamento ou "época", a rede analisa seu desempenho nas tarefas. Ele calcula a diferença entre sua saída e a resposta correta, conhecida como erro. Em seguida, ele ajusta seus parâmetros internos, ou "pesos", para reduzir esse erro na próxima vez. Esse método é essencial para ajustar a precisão da rede neural e é uma estratégia fundamental para aprender a fazer previsões ou tomar decisões melhores

Como funciona a retropropagação?

Agora que você já sabe o que é backpropagation, vamos nos aprofundar em como ele funciona. Abaixo está uma ilustração do algoritmo de retropropagação aplicado a uma rede neural de:

• Duas entradas X1 e X2
• Duas camadas ocultas N1X e N2X, em que X assume os valores 1, 2 e 3
• Uma camada de saída

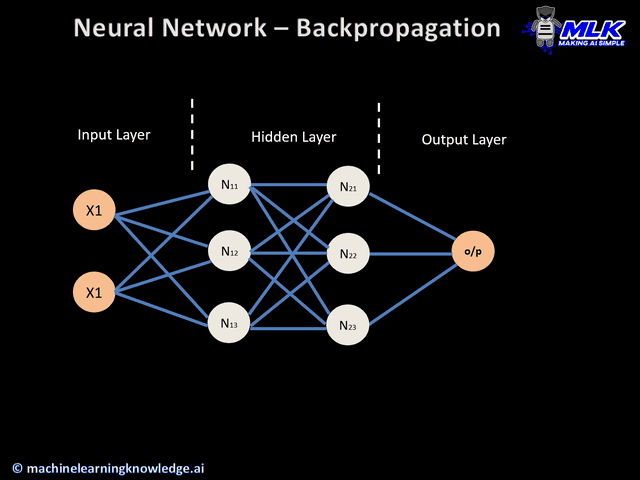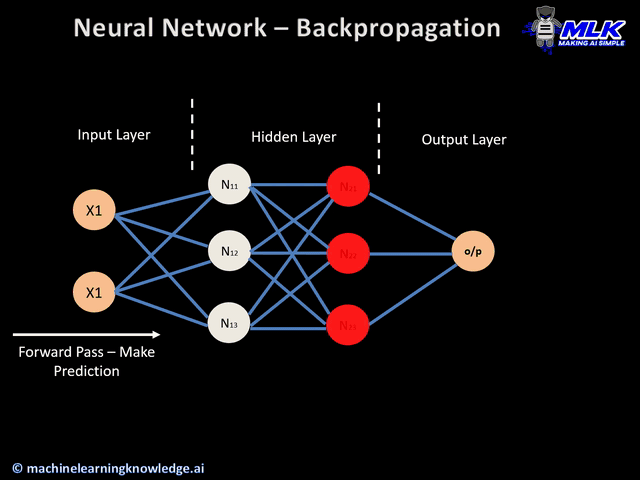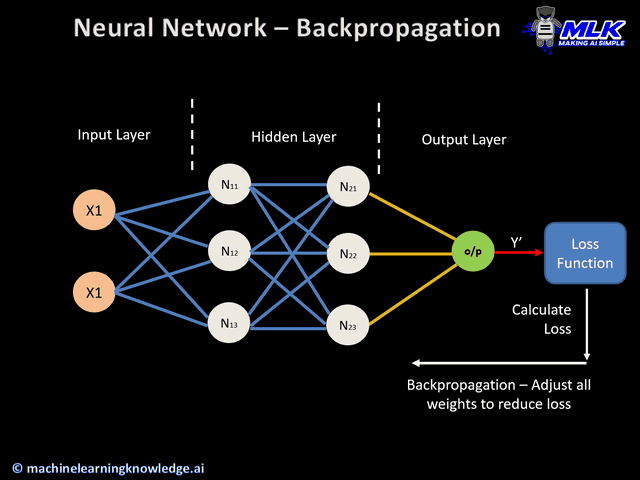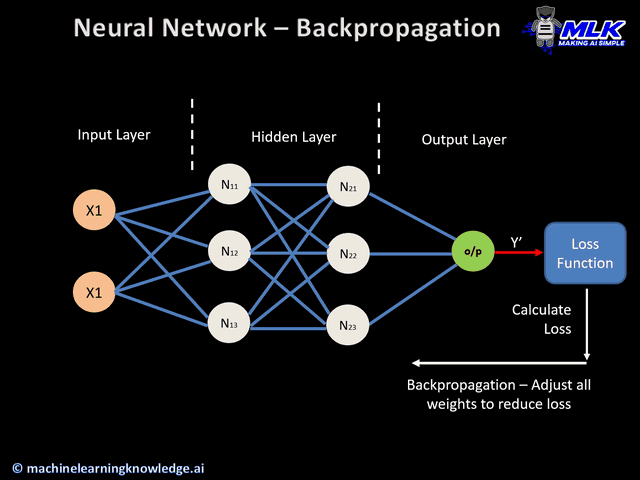
Ilustração de retropropagação(fonte)

Em geral, há quatro etapas principais no algoritmo de retropropagação:

• Passe para frente
• Cálculo de erros
• Passe para trás
• Atualização de pesos

Passagem para frente, cálculo de erro, passagem para trás e atualização de pesos

Vamos entender cada uma dessas etapas da animação acima.

Passe para frente

Essa é a primeira etapa do processo de retropropagação e é ilustrada a seguir:

• Os dados (entradas X1 e X2) são alimentados na camada de entrada
• Em seguida, cada entrada é multiplicada pelo peso correspondente, e os resultados são passados para os neurônios N1X e N2X das camadas ocultas.
• Esses neurônios aplicam uma função de ativação aos inputs ponderados que recebem, e o resultado passa para a próxima camada.

Cálculo de erros

• O processo continua até que a camada de saída gere a saída final (o/p).
• A saída da rede é então comparada com a verdade básica (saída desejada), e a diferença é calculada, resultando em um valor de erro.

Passe para trás

Essa é uma etapa real de retropropagação e não pode ser executada sem as etapas de avanço e cálculo de erro acima. Veja como isso funciona:

• O valor do erro obtido anteriormente é usado para calcular o gradiente da função de perda.
• O gradiente do erro é propagado de volta pela rede, começando pela camada de saída até as camadas ocultas.
• À medida que o gradiente de erro se propaga para trás, os pesos (representados pelas linhas que conectam os nós) são atualizados de acordo com sua contribuição para o erro. Isso envolve tomar a derivada do erro com relação a cada peso, o que indica o quanto uma mudança no peso alteraria o erro.
• A taxa de aprendizado determina o tamanho das atualizações de peso. Uma taxa de aprendizado menor significa que os pesos são atualizados em uma quantidade menor, e vice-versa.

Atualização de pesos

• Os pesos são atualizados na direção oposta ao gradiente, o que dá origem ao nome "descida de gradiente". Seu objetivo é reduzir o erro na próxima passagem para frente.
• Esse processo de passagem para frente, cálculo de erro, passagem para trás e atualização de pesos continua por várias épocas até que o desempenho da rede atinja um nível satisfatório ou pare de melhorar significativamente.

Vantagens da retropropagação

A retropropagação é uma técnica fundamental no treinamento de redes neurais, amplamente apreciada por sua implementação direta, simplicidade de programação e aplicação versátil em várias arquiteturas de rede.

Nosso tutorial Construindo modelos de redes neurais (NN) em R é um ótimo ponto de partida para qualquer pessoa interessada em aprender sobre redes neurais. Ele ensina como criar um modelo de rede neural no R.

Para programadores de Python, o tutorial Recurrent Neural Network Tutorial (RNN) fornece um guia abrangente sobre o modelo de aprendizagem profunda mais popular, o RNN, com experiência prática na criação de um preditor de preços de ações da MasterCard.

Agora, vamos detalhar cada um dos benefícios mencionados anteriormente:

• Facilidade de implementação: acessível por meio de várias bibliotecas de aprendizagem profunda, como Pytorch e Keras, facilitando seu uso em diversos aplicativos.
• Simplicidade de programação: codificação simplificada com abstração de estrutura, reduzindo a necessidade de matemática complexa.
• Flexibilidade: adaptável a diversas arquiteturas, adequado a um amplo espectro de desafios de IA.

Limitações e desafios

Apesar do sucesso do algoritmo de retropropagação, ele tem limitações que podem afetar a eficiência e a eficácia do processo de treinamento de uma rede neural. Vamos explorar algumas dessas restrições:

• Qualidade dos dados: a má qualidade dos dados, incluindo ruído, incompletude ou viés, pode levar a modelos imprecisos, pois o backpropagation aprende exatamente o que lhe é fornecido.
• Duração do treinamento: a retropropagação geralmente exige muito tempo de treinamento, o que pode ser impraticável quando se lida com redes grandes.
• Complexidade baseada em matriz: as operações de matriz na retropropagação são dimensionadas com o tamanho da rede, o que aumenta a demanda computacional e pode ultrapassar os recursos disponíveis.

Implementação da retropropagação

Com todos esses insights sobre o algoritmo de retropropagação, é hora de mergulhar em sua aplicação em um cenário do mundo real com a implementação de uma rede neural para reconhecer dígitos manuscritos do conjunto de dados MNIST.

Esta seção abrange todas as etapas, desde a visualização de dados até o treinamento e a avaliação do modelo. O código-fonte completo está disponível neste DataCamp Workspace.

Sobre o conjunto de dados

O conjunto de dados MNIST é amplamente usado no campo de reconhecimento de imagens. Ele consiste em 70000 imagens em escala de cinza de dígitos manuscritos de 0 a 9, e cada imagem mede 28x28 pixels.

O conjunto de dados está disponível na função mnist do módulo Keras.datasets e é carregado da seguinte forma após a importação da biblioteca mnist:

from keras.datasets import mnist
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()

Análise exploratória de dados

A análise exploratória de dados é uma etapa importante antes da criação de qualquer modelo de aprendizado de máquina ou de aprendizado profundo, pois ajuda a entender melhor a natureza dos dados em questão e, portanto, orienta a escolha do tipo de modelo a ser usado.

As principais tarefas incluem:

• Identificar o número total de dados no conjunto de dados de treinamento e teste.
• Visualização aleatória de alguns dígitos do conjunto de dados de treinamento.
• Visualize a distribuição dos rótulos do conjunto de dados de treinamento.

O conjunto de dados geral consiste em 70000 imagens. A divisão típica do conjunto de dados original é dada da seguinte forma, e não há nenhuma regra específica para isso:

• 70% ou 80% para o conjunto de dados de treinamento
• 30% ou 20% para o conjunto de dados de teste

Algumas divisões podem até ser 90% para treinamento e 10% para teste.

Em nosso cenário, os conjuntos de dados de treinamento e teste são ambos carregados, portanto, não há necessidade de divisão. Vamos observar o tamanho desses conjuntos de dados.

print("Training data")
print(f"- X = {train_images.shape}, y = {train_labels.shape}")
print(f"- Hols {train_images.shape[0]/70000* 100}% of the overall data")

print("\n")

print("Testing data")
print(f"- X = {test_images.shape}, y = {test_labels.shape}")
print(f"- Hols {test_images.shape[0]/70000* 100}% of the overall data")

Características dos conjuntos de dados de treinamento e teste

• O conjunto de dados de treinamento tem 60000 imagens e corresponde a 85,71% do conjunto de dados original.
• O conjunto de dados de teste, por outro lado, tem as 10.000 imagens restantes, ou seja, 14,28% do conjunto de dados original.

Agora, vamos visualizar alguns dígitos aleatórios. Isso é feito com a função auxiliar plot_images, que recebe dois parâmetros principais:

• O número de imagens a serem plotadas e
• O conjunto de dados a ser considerado para a visualização

def plot_images(nb_images_to_plot, train_data):

	# Generate a list of random indices from the training data
	random_indices = random.sample(range(len(train_data)), nb_images_to_plot)

	# Plot each image using the random indices
	for i, idx in enumerate(random_indices):
    	plt.subplot(330 + 1 + i)
    	plt.imshow(train_data[idx], cmap=plt.get_cmap('gray'))

	plt.show()

Queremos visualizar nove imagens dos dados de treinamento, o que corresponde ao seguinte trecho de código:

nb_images_to_plot = 9
plot_images(nb_images_to_plot, train_images)

A execução bem-sucedida do código acima gera os nove dígitos a seguir.

Nove imagens aleatórias do conjunto de dados de treinamento

Os dígitos a seguir são exibidos após a execução da mesma função pela segunda vez, e notamos que eles não são os mesmos; isso se deve à natureza aleatória da função auxiliar.

Nove imagens aleatórias do conjunto de dados de treinamento após uma segunda execução da função

A tarefa final da análise de dados é visualizar a distribuição dos rótulos do conjunto de dados de treinamento usando a função auxiliar plot_labels_distribution.

• No eixo X, temos todos os dígitos possíveis
• No eixo Y, temos o número total desses dígitos

import numpy as np

def plot_labels_distribution(data_labels):
    
	counts = np.bincount(data_labels)

	plt.style.use('seaborn-dark-palette')

	fig, ax = plt.subplots(figsize=(10,5))
	ax.bar(range(10), counts, width=0.8, align='center')
	ax.set(xticks=range(10), xlim=[-1, 10], title='Training data distribution')

	plt.show()

A função é aplicada ao conjunto de dados de treinamento, provando seus rótulos da seguinte forma:

plot_labels_distribution(train_labels)

Abaixo está o resultado, e notamos que todos os dez dígitos estão distribuídos de forma quase uniforme em todo o conjunto de dados, o que é uma boa notícia, o que significa que nenhuma ação adicional é necessária para equilibrar a distribuição dos rótulos.

Pré-processamento de dados

Os dados do mundo real geralmente exigem algum pré-processamento para torná-los adequados aos modelos de treinamento. Há três tarefas principais de pré-processamento aplicadas às imagens de treinamento e teste:

• Normalização da imagem: consiste na conversão de todos os valores de pixel de 0-255 para 0-1. Isso é relevante para uma convergência mais rápida durante o processo de treinamento
• Reformulação de imagens: em vez de ter uma matriz quadrada de 28 por 28 para cada imagem, achatamos cada uma delas em vetores de 784 elementos para torná-las adequadas às entradas da rede neural.
• Codificação de rótulos: converte os rótulos em vetores codificados com um único disparo. Isso evitará os problemas que poderíamos ter com a hierarquia numérica. Dessa forma, o modelo será tendencioso para dígitos maiores.

A lógica geral de pré-processamento é implementada na função auxiliar preprocess_data abaixo:

from keras.utils import to_categorical

def preprocess_data(data, label,
                	vector_size,
                	grayscale_size):
    
	# Normalize to range 0-1
	preprocessed_images = data.reshape((data.shape[0],
                             	vector_size)).astype('float32') / grayscale_size
    
	# One-hot encode the labels
	encoded_labels = to_categorical(label)
    
	return preprocessed_images, encoded_labels

A função é aplicada aos conjuntos de dados usando esses trechos de código:

# Flattening variable
vector_size = 28 * 28

grayscale_size = 255
train_size = train_images.shape[0]
test_size = test_images.shape[0]

# Preprocessing of the training data
train_images, train_labels = preprocess_data(train_images,
                                         	train_labels,
                                         	vector_size,
                                         	grayscale_size)

# Preprocessing of the testing data
test_images, test_labels = preprocess_data(test_images,
                                       	test_labels,
                                       	vector_size,
                                       	grayscale_size)

Agora, vamos observar os valores máximos e mínimos atuais de pixel de ambos os conjuntos de dados:

print("Training data")
print(f"- Maxium Value {train_images.max()} ")
print(f"- Minimum Value {train_images.min()} ")

print("\n")

print("Testing data")
print(f"- Maxium Value {test_images.max()} ")
print(f"- Minimum Value {test_images.min()} ")

O resultado do código é apresentado abaixo, e notamos que a normalização foi realizada com sucesso.

Valores mínimos e máximos de pixel após a normalização

Da mesma forma que os rótulos, finalmente temos uma matriz de uns e zeros, que correspondem aos valores codificados em um único disparo desses rótulos.

# One hot encoding of the test data labels
test_images

Resultado abaixo:

Uma codificação a quente dos rótulos de dados de teste

# One hot encoding of the train data labels
train_labels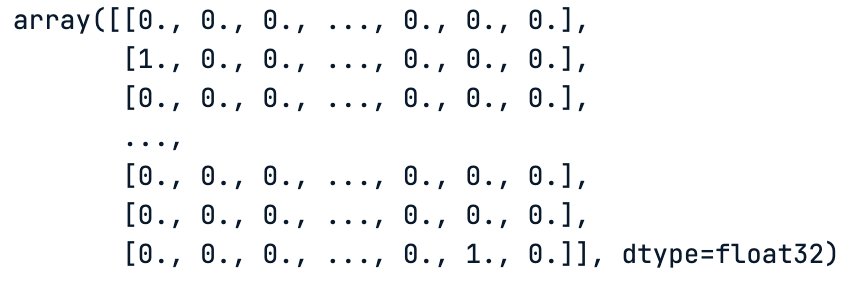

Uma codificação quente dos rótulos dos dados do trem

Estrutura da rede

Como estamos usando uma tarefa de classificação de imagens, uma rede neural de convolução é mais adequada para esse cenário. Antes de codificar qualquer coisa, é importante definir a arquitetura do modelo, e esse é o ponto principal desta seção.

Para saber mais sobre redes neurais convolucionais, nosso tutorial Uma introdução às redes neurais convolucionais (CNNs) é um ótimo recurso inicial. Trata-se de um guia completo para entender as CNNs, seu impacto na análise de imagens e algumas estratégias importantes para combater o excesso de ajuste para aplicações robustas de CNN e de aprendizagem profunda.

A arquitetura para esse caso de uso combina diferentes tipos de camadas para uma classificação eficaz da imagem. Abaixo estão os principais componentes do modelo:

• Camada convolucional: Comece com uma camada usando um filtro pequeno de tamanho 3x3 e 32 filtros para processar as imagens.
• Camada máxima de pooling: Após a camada convolucional, inclua uma camada de pooling máximo para reduzir o tamanho dos mapas de recursos.
• Achatamento: Achatar a saída da camada de pooling em um único vetor, preparando-a para o processo de classificação.
• Camada densa: Adicione uma camada densa com 100 nós entre a saída achatada e a camada final para interpretar os recursos extraídos.
• Camada de saída: Use uma camada de saída com 10 nós, correspondentes às 10 categorias de imagem. Cada nó calcula a probabilidade de uma imagem pertencer a uma dessas categorias.
• Ativação Softmax: Na camada de saída, aplique uma função de ativação softmax para classificação multiclasse.
• Função de ativação do ReLU: Utilize a função de ativação ReLU (Rectified Linear Unit) em todas as camadas para processamento não linear.
• Otimizador: Empregue um otimizador de descida de gradiente estocástico com uma taxa de aprendizado de 0,001 e impulso de 0,95 para ajustar o modelo durante o treinamento.
• Função de perda: Use a função de perda de entropia cruzada categórica, ideal para tarefas de classificação multiclasse.
• Métrica de precisão: Concentre-se na métrica de precisão da classificação, considerando a distribuição equilibrada das classes.

Todas essas informações são implementadas na função auxiliar define_network_architecture. Mas, antes disso, precisamos importar todas as bibliotecas necessárias:

from keras import models
from keras import layers
from tensorflow.keras.optimizers import SGD
from tensorflow.keras.layers import Conv2D
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import MaxPooling2D
from tensorflow.keras.layers import Dense
from tensorflow.keras.layers import Flatten
from tensorflow.keras.layers import BatchNormalization 

Aqui está a implementação da função auxiliar.

hidden_units = 256
nb_unique_labels = 10
vector_size = 784  # Assuming a 28x28 input image for example

def define_network_architecture():

	network = models.Sequential()
	network.add(Dense(vector_size, activation='relu', input_shape=(vector_size,)))  # Input layer
	network.add(Dense(512, activation='relu'))                       	# Hidden layer
	network.add(Dense(nb_unique_labels, activation='softmax'))  

	return network

A implementação do código-fonte é boa, mas é ainda melhor se pudermos ter uma visualização gráfica da rede, e isso é feito usando a função plot_model do módulo keras.utils.vis_utils.

Primeiro, gere a rede a partir da função auxiliar.

network = define_network_architecture()

Em seguida, exiba a representação gráfica. Primeiro salvamos o resultado em um arquivo PNG antes de mostrá-lo; isso facilita o compartilhamento com outras pessoas.

import keras.utils.vis_utils
from importlib import reload
reload(keras.utils.vis_utils)
from keras.utils.vis_utils import plot_model    

import matplotlib.image as mpimg

plot_model(network, to_file='network_architecture.png', show_shapes=True, show_layer_names=True)

img = mpimg.imread('network_architecture.png')
plt.imshow(img)
plt.axis('off')
plt.show()

O resultado é mostrado abaixo.

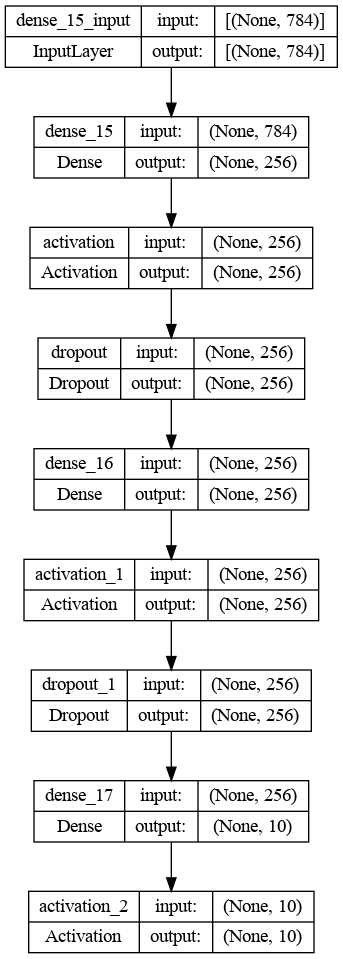
Arquitetura gráfica da rede neural convolucional

Cálculo do delta

Antes de mergulhar no processo de treinamento do modelo, vamos entender como a distribuição do erro delta é calculada usando a arquitetura da rede.

A distribuição do erro delta é a derivada da função de perda com relação à função de ativação de cada nó e indica o quanto a ativação de cada nó contribuiu para o erro final.

A arquitetura acima consiste em três camadas principais:

• Camada de entrada de 784 unidades correspondentes a uma imagem de entrada de 28x28
• A camada oculta de 512 se une à ativação do ReLU
• Camada de saída com 10 unidades, que correspondem ao número de rótulos exclusivos com a função de ativação softmax

Agora, vamos prosseguir com o cálculo do erro delta para cada camada.

Camada de saída

Vamos considerar a saída da camada softmax como big O (O) e os rótulos verdadeiros como Y. Ao usar a perda de entropia cruzada δ de saída, o erro delta se torna:

δ output = O - Y

Essa fórmula vem do cálculo básico de como a perda de entropia cruzada muda quando a saída do softmax muda.

Camada oculta

Para a camada oculta, o erro delta torna-se δ oculto e depende do erro da camada subsequente, que corresponde à camada de saída, e da derivada da função de ativação ReLU.

A derivada do ReLU é 1 para entradas positivas e 0 para entradas negativas, conforme mostrado abaixo.

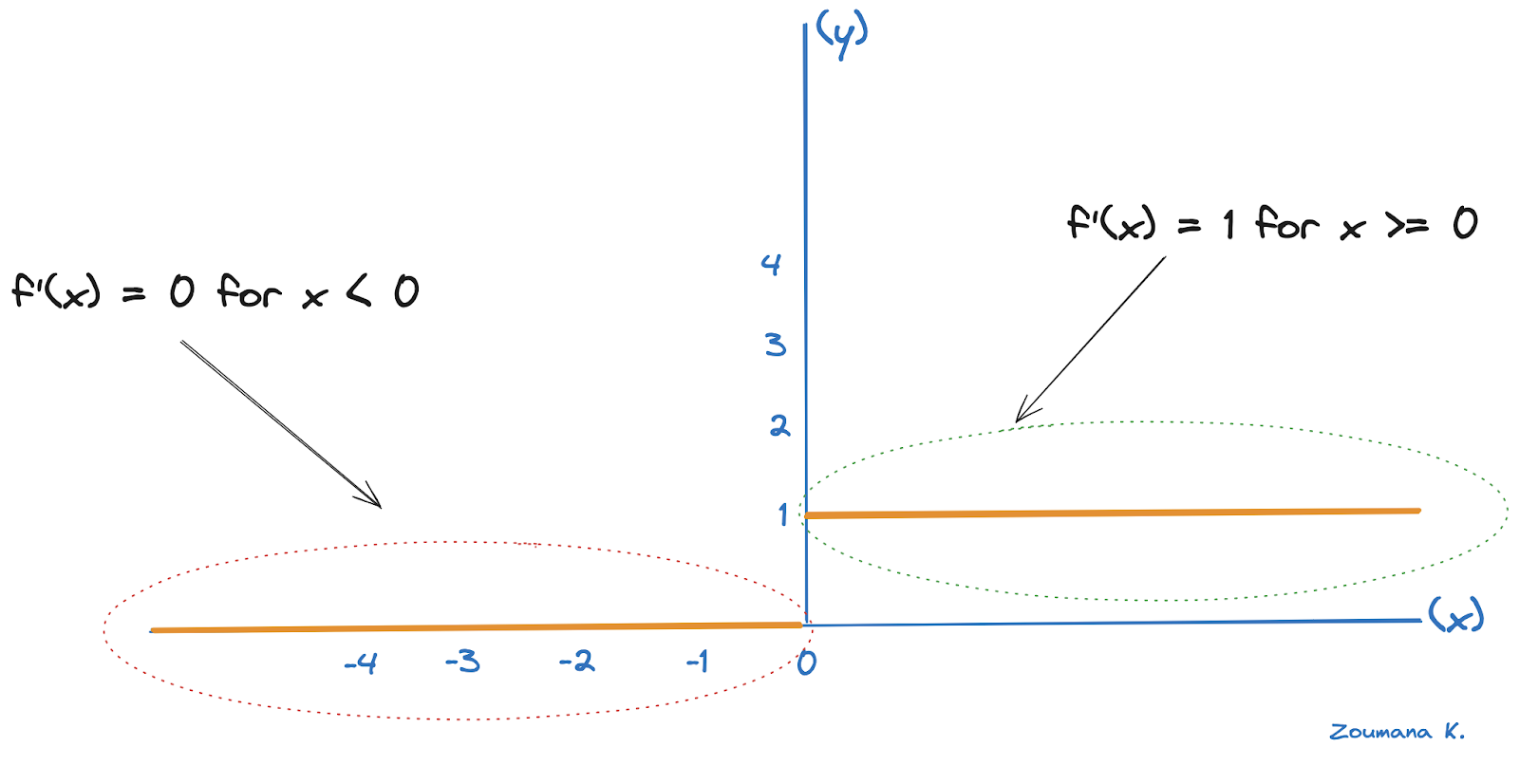
Ilustração derivada do ReLU

Vamos considerar Zhidden como a entrada para a função ReLU na camada oculta e Woutput como os pesos que conectam a camada oculta à camada de saída. O erro delta para a camada oculta, nesse caso, torna-se:

δ oculto =(δ saída . Woutput) ⊙ ReLU'(Zhidden)

• O sinal de ponto "." indica a multiplicação da matriz
• O sinal ⊙ corresponde à multiplicação por elementos
• ReLU'(Zhidden) Corresponde à derivada da ReLU em Zhidden

Camada de entrada

Da mesma forma, se tivéssemos mais camadas ocultas, o processo continuaria de trás para frente, com o erro delta de cada camada dependendo do erro delta da camada subsequente e da derivada de sua função de ativação.

Em um cenário mais geral, para qualquer camada k na rede (exceto a camada de saída), a fórmula para o cálculo do erro delta é

δ _k = (δ _k+1 . W^T_k+1) ⊙ f’(Z_k)

• _WTk+1 corresponde à transposição da matriz de pesos da próxima camada
• f' é a derivada da função de ativação da camada k e
• _Zk é a entrada para a função de ativação na camada k

Compilação da rede

Com esse entendimento do cálculo de erros, vamos compilar a rede para otimizar sua estrutura para o processo de treinamento.

Durante a compilação, precisamos fazer várias escolhas críticas:

• Escolha do algoritmo de otimização: isso envolve a seleção de um algoritmo para otimização de descida de gradiente. Há várias opções, como o Stochastic Gradient Descent (SGD), o Adagrad e o RMSprop, que é usado neste artigo.
• Seleção de uma função de perda: A função de perda, também conhecida como função de custo, é uma parte essencial do treinamento. Ela quantifica o desempenho da rede, e a escolha da função de perda deve estar alinhada com a natureza do problema de classificação ou regressão. O foco está na entropia cruzada categórica devido à natureza multiclasse do problema.
• Escolha de uma métrica de desempenho: Embora seja semelhante a uma função de perda, uma métrica de desempenho é usada principalmente para avaliar a eficácia do modelo no conjunto de dados de teste, e estamos usando a precisão

O código para as três opções acima é fornecido abaixo:

network.compile(optimizer='rmsprop',
            	loss='categorical_crossentropy',
            	metrics=['accuracy'])

Treinamento da rede

Um dos maiores problemas no treinamento de um modelo é o ajuste excessivo, e é fundamental monitorar o modelo durante o processo de treinamento para garantir que ele tenha uma melhor generalização, e uma maneira de fazer isso é o conceito de parada antecipada.

A lógica completa é ilustrada abaixo:

# Fit the model
batch_size = 256
n_epochs = 15
val_split = 0.2
patience_value = 5

# Fit the model with the callback
history = network.fit(train_images, train_labels, validation_split=val_split,
        	epochs=n_epochs, batch_size=batch_size)

O modelo é treinado para 15 épocas usando um tamanho de lote de 256, e 20% dos dados de treinamento são usados para validação do modelo.

Após o treinamento do modelo, o histórico de desempenho do treinamento e da validação é apresentado a seguir.

plt.plot(history.history['accuracy'])
plt.plot(history.history['val_accuracy'])
plt.title('Model accuracy')
plt.ylabel('Accuracy')
plt.xlabel('Epoch')
plt.legend(['Train', 'Validation'], loc='upper left')
plt.show()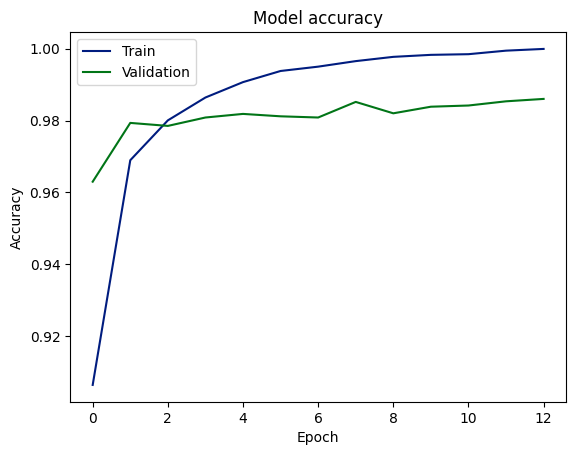

​​

Pontuações de precisão de treinamento e validação

Avaliação de dados de teste

Agora, podemos avaliar o desempenho do modelo nos dados de teste usando a função evaluate do modelo.

loss, acc = network.evaluate(test_images,
                         	test_labels, batch_size=batch_size)

print("\nTest accuracy: %.1f%%" % (100.0 * acc))

Desempenho do modelo em dados de teste

O gráfico indica que o modelo aprendeu a prever resultados com alta precisão, atingindo cerca de 98% nos conjuntos de dados de validação e teste. Isso sugere uma boa generalização do treinamento para dados não vistos. No entanto, a diferença entre a precisão do treinamento e da validação pode ser um sinal de ajuste excessivo, embora a consistência entre a validação e a precisão do teste possa atenuar essa preocupação.

Recomendação

Embora o modelo mostre alta precisão e capacidade de generalização, ainda há espaço para melhorias, e abaixo estão algumas etapas acionáveis para melhorar ainda mais o desempenho.

• Regularização: Integrar métodos de regularização para reduzir o excesso de ajuste.
• Parada antecipada: Utilize a parada antecipada durante o treinamento para evitar o ajuste excessivo.
• Análise de erros: Analisar previsões errôneas para identificar e corrigir problemas subjacentes.
• Teste de diversidade: Teste o modelo em conjuntos de dados variados para confirmar sua robustez.
• Métricas mais amplas: Use precisão, recuperação e pontuação F1 para uma avaliação completa do desempenho, especialmente se os dados forem desequilibrados.

Conclusão

Em resumo, este artigo apresentou uma exploração abrangente da retropropagação, uma técnica essencial no campo do aprendizado de máquina. Começamos com uma definição clara do que é backpropagation e delineamos sua função fundamental no avanço da inteligência artificial.

Em seguida, analisamos o funcionamento da retropropagação e algumas de suas vantagens, como o aumento da eficiência do aprendizado, ao mesmo tempo em que reconhecemos as limitações e os desafios que ela enfrenta.

Em seguida, forneceu orientações detalhadas sobre a configuração e a criação de redes neurais, enfatizando a importância da propagação direta.

Nas seções finais, exploramos as etapas de cálculo de deltas e atualização dos pesos da rede, que são essenciais para refinar o processo de aprendizagem.

De modo geral, este artigo serve como um recurso valioso para qualquer pessoa que queira entender e implementar com eficácia a retropropagação em redes neurais.

Está ansioso para fortalecer suas habilidades em aprendizagem profunda? Nosso curso Aprendizado profundo com PyTorch o ajudará a adquirir a confiança necessária para se aprofundar nas redes neurais e avançar ainda mais em seu conhecimento.