O que são redes neurais recorrentes (RNNs)?
Uma rede neural recorrente (RNN) é o tipo de rede neural artificial (ANN) usada na Siri, da Apple, e na pesquisa por voz do Google. A RNN se lembra de entradas anteriores graças a uma memória interna que é útil para prever preços de ações, gerar textos, transcrições e tradução automática.
Na rede neural tradicional, as entradas e as saídas são independentes umas das outras, enquanto a saída na RNN depende de elementos anteriores dentro da sequência. As redes recorrentes também compartilham parâmetros entre cada camada da rede. Nas redes feedforward, há pesos diferentes em cada nó. Já a RNN compartilha os mesmos pesos em cada camada da rede e, durante a descida do gradiente, os pesos e a base são ajustados individualmente para reduzir a perda.
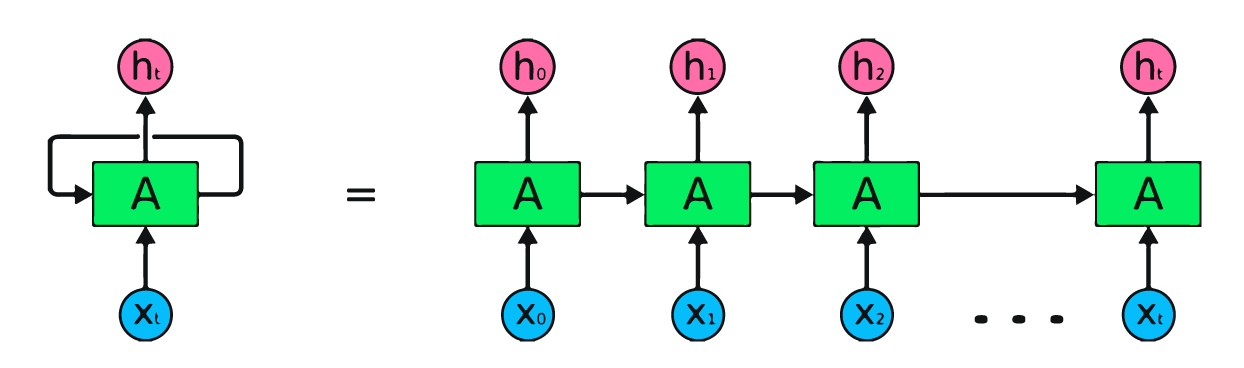
A imagem acima é uma representação simples de redes neurais recorrentes. Se estivermos prevendo os preços das ações usando dados simples [45,56,45,49,50,...], cada entrada de X0 a Xt conterá um valor anterior. Por exemplo: X0 terá 45, X1 terá 56, e esses valores são usados para prever o próximo número em uma sequência.
Como funcionam as redes neurais recorrentes
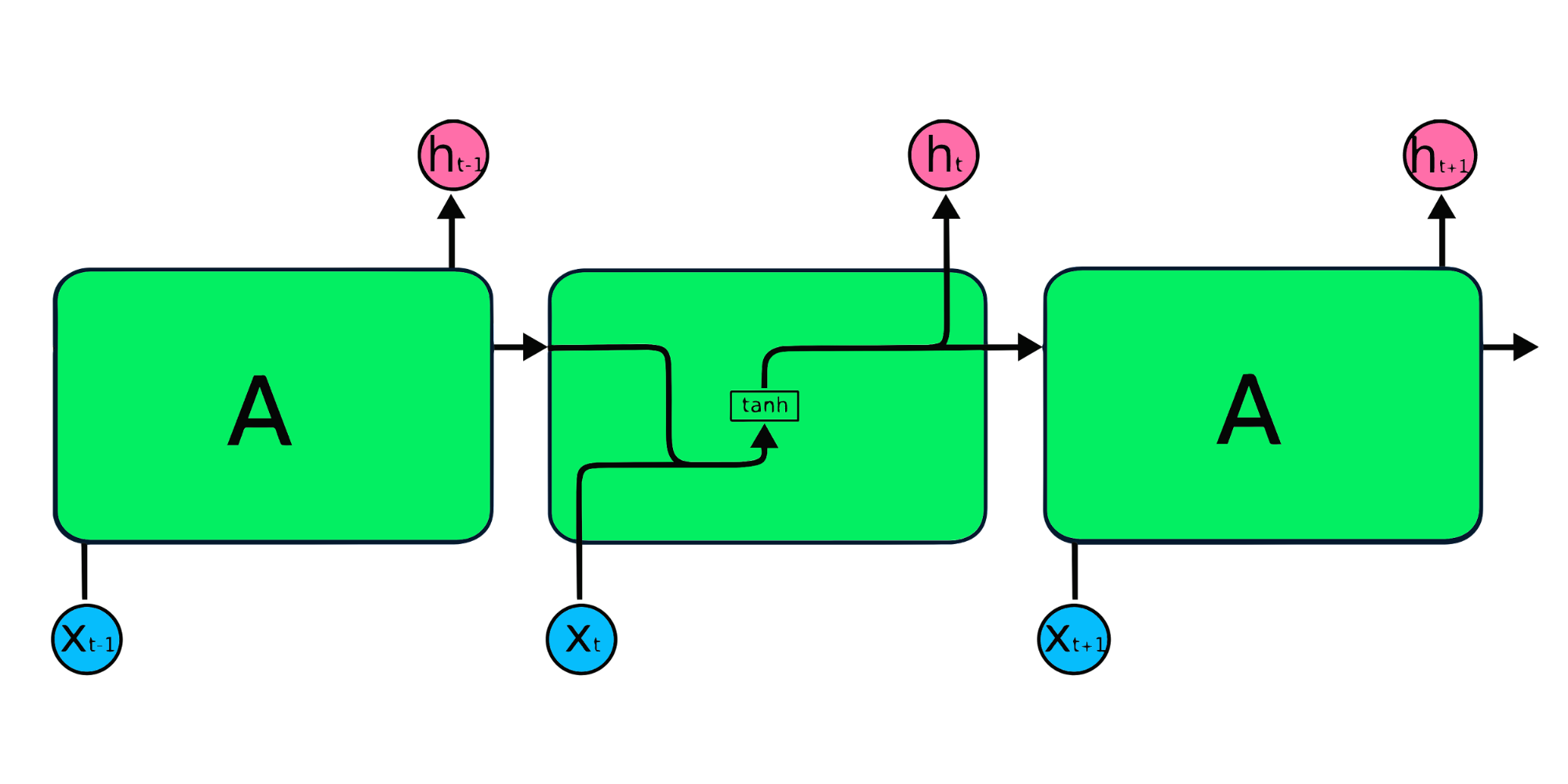
Na RNN, as informações passam pelo loop, de modo que a saída é determinada pela entrada atual e pelas entradas recebidas anteriormente.
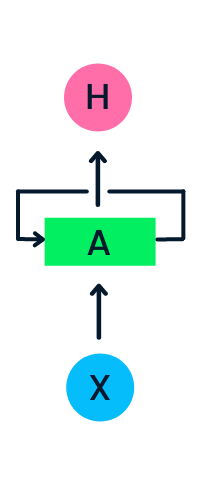
A camada de entrada X processa a entrada inicial e a passa para a camada intermediária A. A camada intermediária é composta de várias camadas ocultas, cada uma com suas funções de ativação, pesos e vieses. Esses parâmetros são padronizados em toda a camada oculta para que, em vez de criar várias camadas ocultas, você crie uma e a repita em loop.
Em vez de usar a retropropagação tradicional, as redes neurais recorrentes usam algoritmos de retropropagação ao longo do tempo (BPTT, Backpropagation Through Time) para determinar o gradiente. Na retropropagação, o modelo ajusta o parâmetro calculando os erros da saída para a camada de entrada. O BPTT soma o erro em cada etapa de tempo, pois a RNN compartilha parâmetros em cada camada. Saiba mais sobre as RNNs e como elas funcionam em O que são redes neurais recorrentes?
Tipos de redes neurais recorrentes
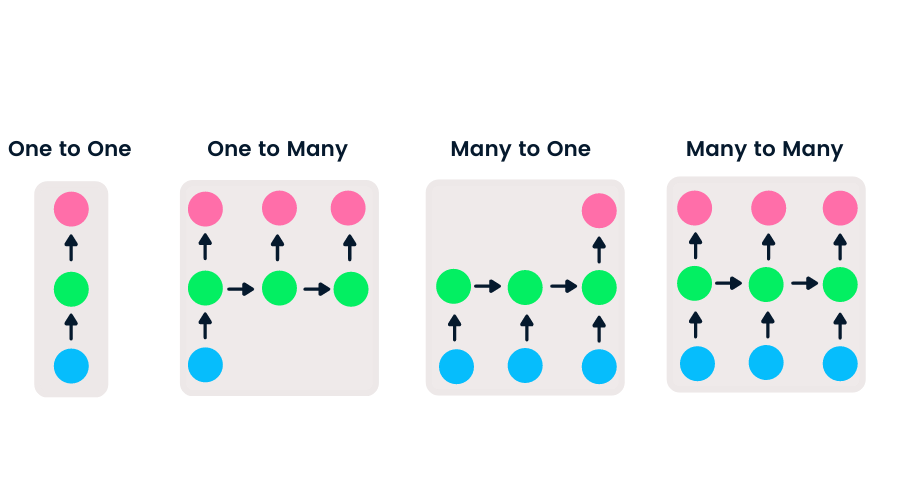
As redes feedforward têm entrada e saída únicas, enquanto as redes neurais recorrentes são flexíveis, pois o tamanho das entradas e saídas pode ser alterado. Essa flexibilidade permite que as RNNs gerem música, classificação de sentimentos e tradução automática.
Há quatro tipos de RNN baseados em diferentes tamanhos de entradas e saídas.
- Uma para uma é uma rede neural simples. Costuma ser usada para problemas de aprendizado de máquina que têm uma única entrada e saída.
- Uma para muitas tem uma única entrada e várias saídas. É usada para gerar legendas de imagens.
- Muitas para uma usa uma sequência de várias entradas e prevê uma única saída. É bem conhecida na classificação de sentimentos, em que a entrada é um texto e a saída é uma categoria.
- Muitas para muitas usa várias entradas e saídas. A aplicação mais comum é a tradução automática.
Cursos de aprendizado de máquina em alta
Introdução ao aprendizado profundo em Python
CNN x RNN
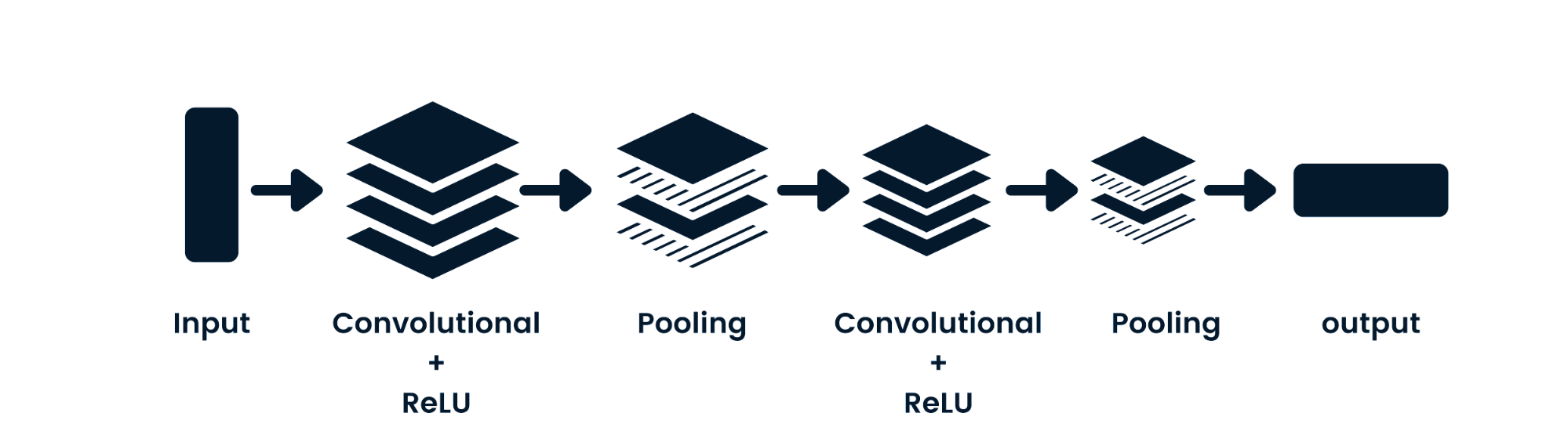
A rede neural convolucional (CNN) é uma rede neural feed-forward capaz de processar dados espaciais. Costuma ser usada em aplicativos de visão computacional, como classificação de imagens. As redes neurais simples são boas em classificações binárias simples, mas não conseguem lidar com imagens com dependências de pixels. A arquitetura dos modelos de CNNs consiste em camadas convolucionais, camadas ReLU, camadas de pooling e camadas de saída totalmente conectadas. Você pode aprender sobre CNNs trabalhando em um projeto como Redes neurais convolucionais em Python.
Principais diferenças entre a CNN e a RNN
- A CNN é aplicável a dados esparsos, como imagens. A RNN é aplicável a séries temporais e dados sequenciais.
- Ao treinar o modelo, a CNN usa uma retropropagação simples, e a RNN usa uma retropropagação ao longo do tempo para calcular a perda.
- Uma RNN pode não ter restrições quanto ao tamanho das entradas e saídas. Já uma CNN tem entradas e saídas finitas.
- Uma CNN tem uma rede feedforward, e uma RNN funciona em loops para lidar com dados sequenciais.
- Uma CNN também pode ser usada para processamento de vídeos e imagens. Uma RNN é usada principalmente para análise de fala e texto.
Limitações das RNNs
Os modelos de RNNs simples geralmente apresentam dois problemas principais. Esses problemas estão relacionados ao gradiente, que é a inclinação da função de perda junto com a função de erro.
- O problema do gradiente de desaparecimento ocorre quando o gradiente se torna tão pequeno que a atualização dos parâmetros se torna insignificante; cedo ou tarde, o algoritmo para de aprender.
- O problema do gradiente explosivo ocorre quando o gradiente se torna muito elevado, o que torna o modelo instável. Nesse caso, gradientes de erro maiores se acumulam, e os pesos do modelo se tornam muito grandes. Esse problema pode causar tempos de treinamento maiores e baixo desempenho do modelo.
A solução simples para esses problemas é reduzir o número de camadas ocultas dentro da rede neural, o que diminui um pouco a complexidade das RNNs. Esses problemas também podem ser resolvidos com o uso de arquiteturas avançadas de RNNs, como LSTM e GRU.
Arquiteturas avançadas de RNNs
Os módulos de repetição de RNNs simples têm uma estrutura básica com uma única camada de tanh. A estrutura simples de RNNs apresenta problemas de memória curta, tendo dificuldades para reter informações de etapas de tempo anteriores em dados sequenciais maiores. Esses problemas podem ser facilmente resolvidos pela memória de curto e longo prazo (LSTM, Long Short-Term Memory) e pela unidade recorrente fechada (GRU, Gated Recurrent Unit), pois elas são capazes de memorizar longos períodos de informações.
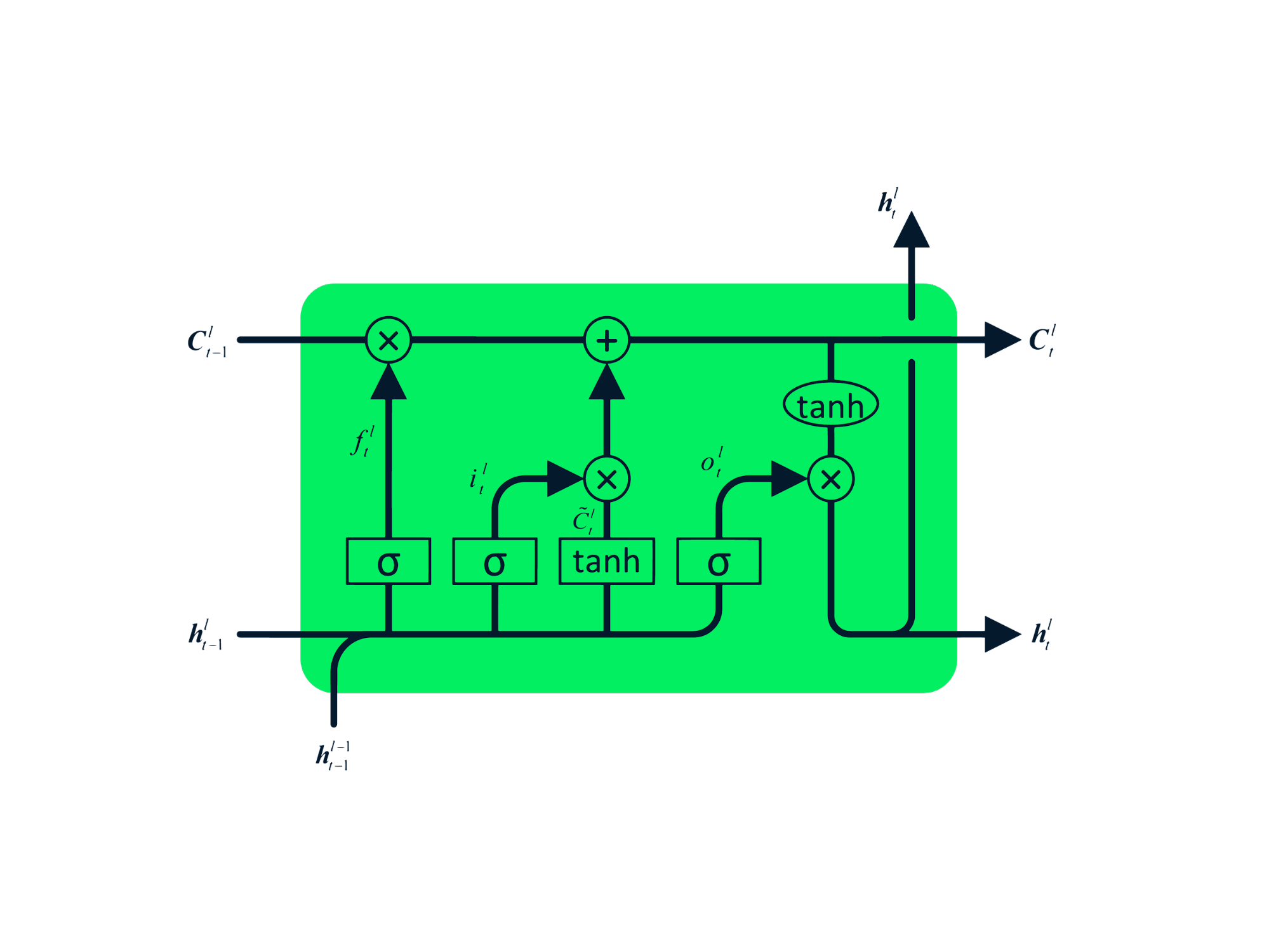
Memória de curto e longo prazo (LSTM)
A memória de curto e longo prazo (LSTM) é o tipo avançado de RNN, que foi projetado para evitar problemas de gradiente decrescente e explosivo. Assim como a RNN, a LSTM tem módulos repetidos, mas a estrutura é diferente. Em vez de ter uma única camada de tanh, a LSTM tem quatro camadas que se comunicam e interagem entre si. Essa estrutura de quatro camadas ajuda a LSTM a reter a memória de longo prazo e pode ser usada em vários problemas sequenciais, como tradução automática, síntese de fala, reconhecimento de fala e reconhecimento de escrita à mão. Você pode adquirir experiência prática em LSTM seguindo o guia: LSTM em Python para previsões de ações.
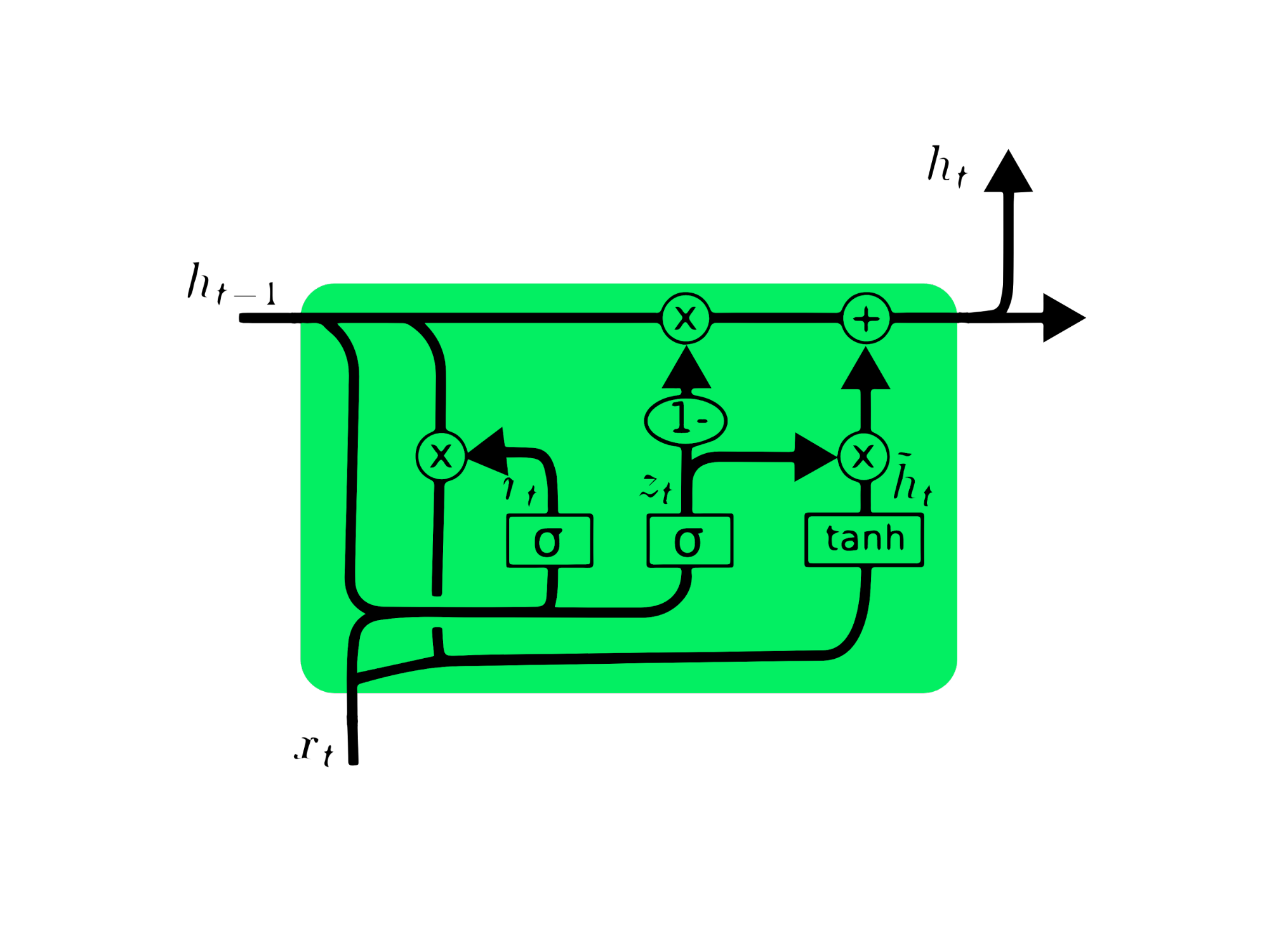
Unidade recorrente fechada (GRU)
A unidade recorrente fechada (GRU) é uma variação da LSTM, pois ambas têm semelhanças de projeto e, em alguns casos, geram resultados semelhantes. A GRU usa uma porta de atualização e uma porta de redefinição para resolver o problema do gradiente que desaparece. Essas portas decidem quais informações são importantes e as transmitem para a saída. As portas podem ser treinadas para armazenar informações de muito tempo atrás, sem desaparecer com o tempo ou remover informações irrelevantes.
Ao contrário da LSTM, a GRU não tem estado de célula Ct. Ela tem apenas um estado oculto ht e, devido à arquitetura simples, a GRU tem um tempo de treinamento menor em comparação com os modelos de LSTM. A arquitetura da GRU é fácil de entender, pois recebe a entrada xt e o estado oculto do registro de data e hora anterior ht-1 e retorna o novo estado oculto ht. Você pode adquirir um conhecimento aprofundado sobre a GRU em Introdução a redes com GRU.
Previsão do preço das ações da MasterCard usando LSTM e GRU
Neste projeto, usaremos o conjunto de dados da Kaggle sobre ações da MasterCard de 25 de maio de 2006 a 11 de outubro de 2021 e treinaremos modelos de LSTM e GRU para prever o preço das ações. Este é um tutorial simples baseado em um projeto no qual vamos analisar dados, pré-processar os dados para treiná-los com modelos avançados de RNN e, por fim, avaliar os resultados.
O projeto requer Pandas e Numpy para manipulação de dados, Matplotlib.pyplot para visualização de dados, scikit-learn para dimensionamento e avaliação e TensorFlow para modelagem. Também vamos definir sementes para garantir a reprodutibilidade.
# Importing the libraries
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_squared_error
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, LSTM, Dropout, GRU, Bidirectional
from tensorflow.keras.optimizers import SGD
from tensorflow.random import set_seed
set_seed(455)
np.random.seed(455)
Análise de dados
Nesta parte, importaremos o conjunto de dados da MasterCard adicionando a coluna Date ao índice e convertendo-a para o formato DateTime. Também eliminaremos colunas irrelevantes do conjunto de dados, pois estamos interessados apenas nos preços das ações, no volume e na data.
O conjunto de dados tem Date como índice e Open, High, Low, Close e Volume como colunas. Parece que importamos com sucesso um conjunto de dados limpo.
dataset = pd.read_csv(
"data/Mastercard_stock_history.csv", index_col="Date", parse_dates=["Date"]
).drop(["Dividends", "Stock Splits"], axis=1)
print(dataset.head())
Open High Low Close Volume
Date
2006-05-25 3.748967 4.283869 3.739664 4.279217 395343000
2006-05-26 4.307126 4.348058 4.103398 4.179680 103044000
2006-05-30 4.183400 4.184330 3.986184 4.093164 49898000
2006-05-31 4.125723 4.219679 4.125723 4.180608 30002000
2006-06-01 4.179678 4.474572 4.176887 4.419686 62344000
A função .describe() nos ajuda a analisar os dados de forma detalhada. Vamos nos concentrar na coluna High, pois vamos usá-la para treinar o modelo. Também podemos escolher as colunas Close ou Open como variável independente (feature) do modelo, mas High faz mais sentido, pois nos fornece informações sobre o quanto os valores da ação subiram em um determinado dia.
O preço mínimo da ação é de US$ 4,10 e o máximo é de US$ 400,5. A média é de US$ 105,9 e o desvio padrão é de US$ 107,3, o que significa que as ações têm alta variação.
print(dataset.describe())
Open High Low Close Volume
count 3872.000000 3872.000000 3872.000000 3872.000000 3.872000e+03
mean 104.896814 105.956054 103.769349 104.882714 1.232250e+07
std 106.245511 107.303589 105.050064 106.168693 1.759665e+07
min 3.748967 4.102467 3.739664 4.083861 6.411000e+05
25% 22.347203 22.637997 22.034458 22.300391 3.529475e+06
50% 70.810079 71.375896 70.224002 70.856083 5.891750e+06
75% 147.688448 148.645373 146.822013 147.688438 1.319775e+07
max 392.653890 400.521479 389.747812 394.685730 3.953430e+08
Usando .isna().sum(), podemos determinar os valores ausentes no conjunto de dados. Parece que o conjunto de dados não tem valores ausentes.
dataset.isna().sum()
Open 0
High 0
Low 0
Close 0
Volume 0
dtype: int64
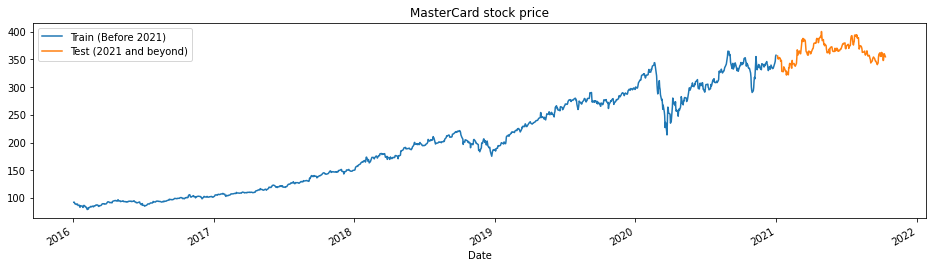
A função train_test_plot recebe três argumentos – dataset, tstart e tend – e traça um gráfico de linha simples. O tstart e o tend são limites de tempo em anos. Podemos alterar esses argumentos para analisar períodos específicos. O gráfico de linhas é dividido em duas partes: treinamento e teste. Isso nos permite decidir a distribuição do conjunto de dados de teste.
Os preços das ações da MasterCard vêm subindo desde 2016. Houve uma queda no primeiro trimestre de 2020, mas a posição se estabilizou na segunda metade do ano. Nosso conjunto de dados de teste consiste em um ano, de 2021 a 2022, e o restante do conjunto de dados é usado para treinamento.
tstart = 2016
tend = 2020
def train_test_plot(dataset, tstart, tend):
dataset.loc[f"{tstart}":f"{tend}", "High"].plot(figsize=(16, 4), legend=True)
dataset.loc[f"{tend+1}":, "High"].plot(figsize=(16, 4), legend=True)
plt.legend([f"Train (Before {tend+1})", f"Test ({tend+1} and beyond)"])
plt.title("MasterCard stock price")
plt.show()
train_test_plot(dataset,tstart,tend)
Pré-processamento dos dados
A função train_test_split divide o conjunto de dados em dois subconjuntos: training_set e test_set.
def train_test_split(dataset, tstart, tend):
train = dataset.loc[f"{tstart}":f"{tend}", "High"].values
test = dataset.loc[f"{tend+1}":, "High"].values
return train, test
training_set, test_set = train_test_split(dataset, tstart, tend)
Usaremos a função MinMaxScaler para padronizar nosso conjunto de treinamento, o que nos ajuda a evitar os valores discrepantes ou anomalias. Você também pode tentar usar o StandardScaler ou qualquer outra função escalar para normalizar os dados e melhorar o desempenho do modelo.
sc = MinMaxScaler(feature_range=(0, 1))
training_set = training_set.reshape(-1, 1)
training_set_scaled = sc.fit_transform(training_set)
A função split_sequence usa um conjunto de dados de treinamento e o converte em entradas (X_train) e saídas (y_train).
Por exemplo: se a sequência for [1,2,3,4,5,6,7,8,9,10,11,12] e n_step for três, você converterá a sequência em três registros de data e hora de entrada e uma saída, conforme mostrado abaixo:
| X | y |
|---|---|
| 1,2,3 | 4 |
| 2,3,4 | 5 |
| 3,4,5 | 6 |
| 4,5,6 | 7 |
| … | … |
Neste projeto, estamos usando 60 n_steps. Também podemos reduzir ou aumentar o número de etapas para otimizar o desempenho do modelo.
def split_sequence(sequence, n_steps):
X, y = list(), list()
for i in range(len(sequence)):
end_ix = i + n_steps
if end_ix > len(sequence) - 1:
break
seq_x, seq_y = sequence[i:end_ix], sequence[end_ix]
X.append(seq_x)
y.append(seq_y)
return np.array(X), np.array(y)
n_steps = 60
features = 1
# split into samples
X_train, y_train = split_sequence(training_set_scaled, n_steps)
Estamos trabalhando com séries univariadas, portanto o número de variáveis independentes (features) é igual a um, e precisamos remodelar o X_train para que se ajuste ao modelo de LSTM. O X_train tem [amostras, intervalos de tempo], e vamos reformulá-lo para [amostras, intervalos de tempo, variáveis independentes].
# Reshaping X_train for model
X_train = X_train.reshape(X_train.shape[0],X_train.shape[1],features)
Modelo de LSTM
O modelo consiste em uma única camada oculta de LSTM e uma camada de saída. Você pode fazer testes com o número de unidades, pois mais unidades proporcionam melhores resultados. Para este experimento, definiremos as unidades de LSTM como 125, tanh como activation (ativação) e vamos definir o tamanho da entrada.
Nota do autor: A biblioteca do Tensorflow é fácil de usar, portanto não precisamos criar modelos de LSTM ou GRU do zero. Simplesmente usaremos os módulos de LSTM ou GRU para construir o modelo.
Por fim, compilaremos o modelo com um otimizador RMSprop e o erro quadrático médio como função de perda.
# The LSTM architecture
model_lstm = Sequential()
model_lstm.add(LSTM(units=125, activation="tanh", input_shape=(n_steps, features)))
model_lstm.add(Dense(units=1))
# Compiling the model
model_lstm.compile(optimizer="RMSprop", loss="mse")
model_lstm.summary()
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
lstm (LSTM) (None, 125) 63500
_________________________________________________________________
dense (Dense) (None, 1) 126
=================================================================
Total params: 63,626
Trainable params: 63,626
Non-trainable params: 0
_________________________________________________________________
O modelo será treinado em 50 épocas com 32 tamanhos de lote. Você pode alterar os hiperparâmetros para reduzir o tempo de treinamento ou melhorar os resultados. O treinamento do modelo foi concluído com sucesso e com a melhor perda possível.
model_lstm.fit(X_train, y_train, epochs=50, batch_size=32)
Epoch 50/50
38/38 [==============================] - 1s 30ms/step - loss: 3.1642e-04
Resultados
Vamos repetir o pré-processamento e normalizar o conjunto de teste. Em primeiro lugar, vamos transformar e, em seguida, dividir o conjunto de dados em amostras, remodelá-lo, prever e transformar inversamente as previsões em formato padrão.
dataset_total = dataset.loc[:,"High"]
inputs = dataset_total[len(dataset_total) - len(test_set) - n_steps :].values
inputs = inputs.reshape(-1, 1)
#scaling
inputs = sc.transform(inputs)
# Split into samples
X_test, y_test = split_sequence(inputs, n_steps)
# reshape
X_test = X_test.reshape(X_test.shape[0], X_test.shape[1], features)
#prediction
predicted_stock_price = model_lstm.predict(X_test)
#inverse transform the values
predicted_stock_price = sc.inverse_transform(predicted_stock_price)
A função plot_predictions gera um gráfico de linha real versus previsto. Isso nos ajuda a visualizar a diferença entre os valores reais e os previstos.
A função return_rmse recebe argumentos de teste e previsão e imprime a métrica de erro quadrático médio (rmse).
def plot_predictions(test, predicted):
plt.plot(test, color="gray", label="Real")
plt.plot(predicted, color="red", label="Predicted")
plt.title("MasterCard Stock Price Prediction")
plt.xlabel("Time")
plt.ylabel("MasterCard Stock Price")
plt.legend()
plt.show()
def return_rmse(test, predicted):
rmse = np.sqrt(mean_squared_error(test, predicted))
print("The root mean squared error is {:.2f}.".format(rmse))
De acordo com o gráfico de linhas abaixo, o modelo de LSTM de camada única teve um bom desempenho.
plot_predictions(test_set,predicted_stock_price)
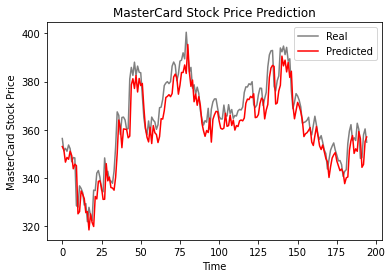
Os resultados parecem promissores, pois o modelo obteve um rmse de 6,70 no conjunto de dados de teste.
return_rmse(test_set,predicted_stock_price)
>>> The root mean squared error is 6.70.
Modelo de GRU
Vamos manter tudo igual e apenas substituir a camada de LSTM pela camada de GRU para comparar adequadamente os resultados. A estrutura do modelo contém uma única camada de GRU com 125 unidades e uma camada de saída.
model_gru = Sequential()
model_gru.add(GRU(units=125, activation="tanh", input_shape=(n_steps, features)))
model_gru.add(Dense(units=1))
# Compiling the RNN
model_gru.compile(optimizer="RMSprop", loss="mse")
model_gru.summary()
Model: "sequential_5"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
gru_4 (GRU) (None, 125) 48000
_________________________________________________________________
dense_5 (Dense) (None, 1) 126
=================================================================
Total params: 48,126
Trainable params: 48,126
Non-trainable params: 0
_________________________________________________________________
O modelo foi treinado com sucesso com 50 épocas e um tamanho de lote de 32.
model_gru.fit(X_train, y_train, epochs=50, batch_size=32)
Epoch 50/50
38/38 [==============================] - 1s 29ms/step - loss: 2.6691e-04
Resultados
Como podemos ver, os valores reais e previstos são relativamente próximos. O gráfico de linhas previsto quase se ajusta aos valores reais.
GRU_predicted_stock_price = model_gru.predict(X_test)
GRU_predicted_stock_price = sc.inverse_transform(GRU_predicted_stock_price)
plot_predictions(test_set, GRU_predicted_stock_price)
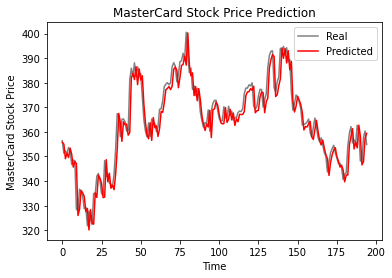
O modelo de GRU obteve rmse igual a 5,50 no conjunto de dados de teste, o que representa uma melhoria em relação ao modelo de LSTM.
return_rmse(test_set,GRU_predicted_stock_price)
>>> The root mean squared error is 5.50.
Conclusão
O mundo está se movendo em direção a soluções híbridas. Os cientistas de dados estão usando redes híbridas CNN-RNN na área de legendas de imagens, detecção de emoções, legendagem de vídeos e sequenciamento de DNA. As redes híbridas fornecem características visuais e temporais para o modelo. Saiba mais sobre RNNs fazendo o curso: Redes neurais recorrentes para modelagem de linguagem em Python.
A primeira metade do tutorial aborda os conceitos básicos de redes neurais recorrentes, suas limitações e soluções na forma de arquitetura mais avançada. A segunda parte do tutorial trata do desenvolvimento de previsões de preços de ações da MasterCard usando modelos de LSTM e GRU. Os resultados mostram claramente que o modelo de GRU teve um desempenho melhor do que o de LSTM, com uma estrutura e hiperparâmetros semelhantes.
Esse projeto está disponível no espaço de trabalho do DataCamp.



