Weighted Average Formula: A Complete Guide with Practical Applications

Weighted averages show up everywhere in data analysis, from calculating your GPA to determining portfolio returns. Unlike simple averages that treat all data points equally, weighted averages recognize that some values deserve more influence than others. This makes them incredibly useful when you're dealing with data of varying importance or frequency.

What Is a Weighted Average?

A weighted average assigns different levels of importance to individual data points based on predetermined weights. While a simple average treats all values equally, a weighted average multiplies each value by its corresponding weight before calculating the final result.

Here's the key insight: weights directly control how much each data point influences the final average. A data point with a higher weight pulls the result closer to its value, while lower-weighted points have less impact. This gives you much more control over your calculations and often produces more meaningful results.

Weighted averages differ from simple averages in one important way: they account for the relative significance of each data point rather than assuming all points are equally important.

Understanding The Weighted Average Formula

Now that we've established what weighted averages are and why they matter, let's dive into the mathematical foundation that makes them work.

Mathematical definition and core principles

The weighted average formula combines each data point with its corresponding weight:

Where Σ represents the sum of all terms. Each value gets multiplied by its weight, then you add up all these products and divide by the total of all weights. 

In most practical contexts (probabilities, frequencies, and shares), weights are non-negative and often normalized to sum to 1 (or to the total count). In specialized methods, negative weights can appear, but they may yield counterintuitive results and should be used with care. Always ensure the sum of weights is greater than zero to avoid division by zero.

This formula ensures that higher-weighted values have proportionally more influence on the final result. For example, if one data point has a weight of 10 and another has a weight of 1, the first point contributes ten times more to the final average.

Normalization and special cases

Normalization means scaling weights so they sum to 1, making each weight directly interpretable as a percentage contribution. When $(sum_i w_i = 1)$, the weighted average simplifies to $(sum_i w_i x_i)$. In probability contexts, these weights are probabilities and the weighted average is the expected value.

This normalized approach is especially useful in probability contexts, where weights represent probabilities that must sum to 1. In these cases, the weighted average becomes the expected value of the distribution.

Why and When to Use Weighted Averages

With the mathematical groundwork in place, you might be wondering when weighted averages become the better choice over simple averages. The answer lies in recognizing when your data naturally has varying levels of significance.

Weighted averages become essential when your data points naturally have different levels of importance or frequency. You'll find weighted averages work better than simple averages when data points represent different sample sizes, time periods, or levels of reliability. For instance, when calculating average test scores across different class sizes, larger classes should influence the overall average more than smaller ones.

Weighted averages are particularly valuable in financial calculations (portfolio returns), academic grading (different assignment weights), survey analysis (demographic adjustments), and inventory management (cost averaging across different purchase quantities).

Common Challenges with Weighted Averages

While weighted averages are powerful tools, they come with their own set of potential pitfalls that you'll want to navigate carefully.

Weight selection

The most critical challenge lies in choosing appropriate weights, which requires domain expertise and careful consideration of what each data point represents. Poor weight selection can skew results dramatically and lead to misleading conclusions.

For example, if you're calculating customer satisfaction scores and accidentally assign higher weights to less reliable data sources, your final average won't accurately reflect true customer sentiment. Always ensure your weights reflect the actual importance or reliability of each data point.

Computational pitfalls

Beyond weight selection, common computational errors include using zero weights (which removes data points), negative weights (which can produce counterintuitive results), and forgetting to normalize weights when necessary. Division by zero occurs when all weights are zero.

Always double-check your weight assignments and ensure proper normalization, especially when working with percentage-based weights that should sum to 100%.

How to Calculate Weighted Average in Excel and Python

Having covered the theory and potential challenges, let's turn to the practical side and see how to implement weighted averages using popular tools you're likely already familiar with.

How to calculate weighted average in Excel

Excel makes weighted average calculations straightforward using the SUMPRODUCT() and SUM() functions. The formula structure is: 

	=SUMPRODUCT(values, weights)/SUM(weights)	

For example, if values are in A2:A6 and weights in B2:B6: =SUMPRODUCT(A2:A6, B2:B6) / SUM(B2:B6) 

Tip: Keep weight units consistent. If weights are percentages, either store them as decimals (e.g., 0.6) or as whole numbers (e.g., 60) but use the same units in both numerator and denominator. 

How to calculate weighted average in Python

For those working in Python, the numpy library provides an elegant solution, though you can also calculate weighted averages manually:

	import numpy as np	# Define values and weights	values = [85, 92, 78, 95]	weights = [0.2, 0.3, 0.25, 0.25]	# Calculate weighted average	weighted_avg = np.average(values, weights=weights)	print(f"Weighted average: {weighted_avg:.2f}")	# Alternative manual calculation	manual_calc = sum(v * w for v, w in zip(values, weights)) / sum(weights)	print(f"Manual calculation: {manual_calc:.2f}")	

Weighted Average Formula in Real, Domain-Specific Applications

Now that you know how to calculate weighted averages, let's explore how they solve real problems across different fields. These examples will help you recognize situations where weighted averages can improve your own analysis.

Educational grading system

Academic grading systems commonly use weighted averages to balance different types of assessments. A typical course might weigh exams at 60%, homework at 25%, and participation at 15%.

If a student scores 88 on exams, 95 on homework, and 92 on participation, their final grade would be: (88×0.6) + (95×0.25) + (92×0.15) = 90.35. This approach ensures that more important assessments have a greater impact on the final grade.

Financial inventory valuation

In business applications, companies often use the weighted average cost (WAC) method to value inventory when goods are purchased at different prices during a period. Unlike a simple arithmetic mean, WAC incorporates purchase quantities, which smooths out price fluctuations and provides a consistent cost basis for financial reporting.

For example, if a company buys 100 units at $10 and 300 units at $12, the weighted average cost is $11.50, not $11.00 as a simple average would suggest.

Financial analysis

In finance, weighted averages extend far beyond inventory. Portfolio management relies on them to calculate expected returns and risks, with each asset’s weight based on its proportion of the total portfolio value. This ensures larger holdings have more influence than smaller ones.

Similarly, the Weighted Average Cost of Capital (WACC) applies the same principle: it represents a firm’s average cost of financing by weighting the costs of debt and equity in proportion to their share of the capital structure. WACC is a key input in valuation models and investment decisions, as it serves as the company’s hurdle rate for generating returns.

Statistical surveying

In the research world, survey analysis uses weighted averages to adjust for demographic imbalances and ensure representative results. If your survey under-samples certain age groups, you can weight responses to match the actual population distribution.

This adjustment helps eliminate sampling bias and produces more accurate insights about the broader population you're studying.

Inventory accounting

Returning to practical business applications, the moving average method in inventory accounting uses weighted averages to determine cost of goods sold. Each new purchase updates the average cost per unit based on remaining inventory and new additions.

This approach smooths price volatility and provides stable cost estimates for financial reporting, making it easier to track profitability trends over time.

Area-weighted building inputs and other specialized contexts

Beyond these common applications, engineering applications often use area-weighted averages for building energy calculations, where different zones contribute to overall building performance based on their size.

Similar concepts appear in geographic information systems (GIS) for spatial analysis and in manufacturing for quality control across different production areas.

Comparative Analysis With Other Averages

With all these applications in mind, you might be wondering how to choose between weighted averages and other averaging methods. Understanding these distinctions will help you select the right approach for your specific situation.

Arithmetic vs. weighted mean

Arithmetic means assume all data points are equally important and representative. Weighted averages explicitly account for differences in importance, reliability, or frequency among data points.

Choose weighted averages when your data naturally has different levels of significance or when you need to adjust for sampling imbalances. Use simple arithmetic means when all data points truly deserve equal consideration.

Geometric mean

Geometric means work best for multiplicative data like growth rates or ratios, where you want to find the average rate of change over time. However, geometric means don't naturally accommodate weighting.

While you can create weighted geometric means using logarithms, this approach is mathematically complex and less intuitive than weighted arithmetic means for most applications.

Advantages and Disadvantages of Weighted Averages

Before diving into more advanced topics, it's worth stepping back to consider the broader trade-offs involved in using weighted averages.

Pros of weighted averages

Weighted averages provide superior accuracy when data points naturally vary in importance or reliability. They offer flexibility to adjust calculations based on domain knowledge and can better represent real-world scenarios where not all observations are equal.

This approach excels in situations requiring demographic adjustments, portfolio analysis, or any context where sample sizes or measurement confidence varies across data points.

Cons of weighted averages

The main limitation is subjectivity in weight selection, which can introduce bias if done poorly. Weighted averages are also more sensitive to outliers with high weights and prone to errors if weights are assigned incorrectly.

Additionally, they require more computational effort and domain expertise compared to simple averages, making them unnecessarily complex for situations where equal weighting is appropriate.

More Advanced and Theoretical Extensions

For readers interested in pushing beyond basic applications, weighted averages extend into more sophisticated mathematical territory that opens up additional analytical possibilities.

Continuous weighted averages

Weighted averages can extend to continuous functions using integral calculus. Instead of discrete weights and values, you integrate over continuous weight and value functions:

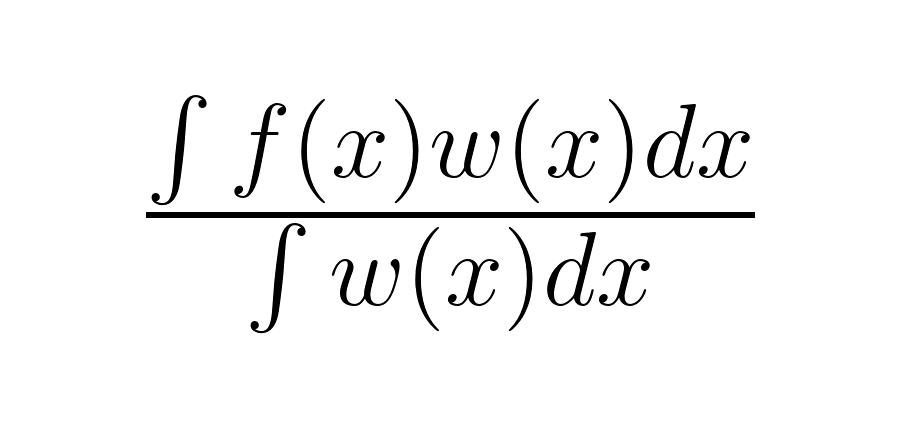
This approach appears in physics for calculating centers of mass and in probability theory for continuous distributions.

Expected value in probability

Building on this mathematical foundation, in probability theory, expected value represents the weighted average of all possible outcomes, where weights are the probabilities of each outcome occurring.

Expected values help predict long-term outcomes in uncertain situations, from casino games to investment returns, making them essential tools for risk assessment and decision-making.

Conclusion

Weighted averages provide a more nuanced and accurate approach to data analysis when your observations naturally vary in importance, frequency, or reliability. Throughout this guide, we've seen how they enhance decision-making across diverse fields. From academic grading to portfolio management, by properly accounting for the relative significance of different data points.

As you begin incorporating weighted averages into your own analysis, remember that the technique's power comes from its ability to reflect real-world complexities where not all data deserves equal consideration. Whether you're calculating grades, analyzing portfolios, or processing survey data, weighted averages help you make more informed decisions by giving appropriate influence to the information that matters most.

Consider exploring our Advanced Excel Functions course to deepen your spreadsheet skills, or check out our Descriptive Statistics Cheat Sheet for quick reference on statistical concepts like these.