Geometric Mean: A Measure for Growth and Compounding

Have you ever calculated the average of your yearly investment returns, only to find that your actual overall return doesn't quite match up? This common scenario in finance highlights the importance of understanding and applying the geometric mean – a useful measure that often proves more appropriate than the widely-used arithmetic mean when dealing with rates of change and compounding effects.

In this tutorial, we'll explore the concept of the geometric mean and its role in data analysis, particularly in fields like finance, biology, and data science. We will also examine scenarios where it outperforms other measures of central tendency.

What is the Geometric Mean?

The geometric mean is a type of average that is particularly useful when working with sets of positive numbers, especially those involving multiplication or exponential growth. Unlike the more common arithmetic mean, which adds numbers and divides by the count, the geometric mean is particularly adept at handling datasets involving multiplicative relationships or exponential growth.

Here are some of the fields where the geometric mean is valuable:

1. Finance: It's commonly used to calculate average rates of return over multiple periods. Unlike the arithmetic mean, the geometric mean accounts for compounding, making it more accurate for financial calculations.
2. Biology: In population growth studies, the geometric mean is used to calculate average growth rates over time.
3. Geometry: One of its most elegant appearances is in right triangles, where the altitude to the hypotenuse embodies the geometric mean of the segments it creates on that hypotenuse. Also, the geometric mean represents the side length of a square that would have the same area as a given rectangle, providing a way to "square" rectangular areas.

As you can see, the geometric mean is a valuable tool in both everyday calculations and also in more abstract mathematical concepts.

How to Calculate the Geometric Mean

There are several methods to compute the geometric mean, each with its own advantages depending on the situation.

The geometric mean formula

The most straightforward way to calculate the geometric mean is by using the standard formula: 

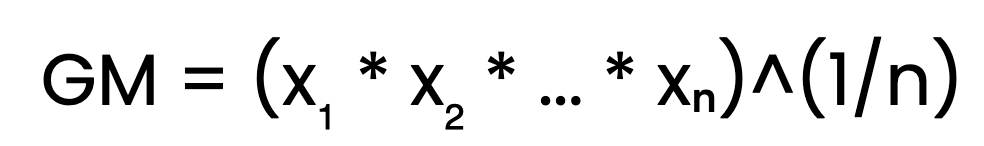
Here, x₁, x₂, ..., xₙ are the positive numbers in the dataset, and n is the count of numbers. To obtain the geometric mean we multiply all the values together and take the nth root of the product, where n is the number of values. Let's showcase this through an example. Consider the numbers 2, 4, and 8. To find their geometric mean:

1. Multiply the numbers: 2 * 4 * 8 = 64
2. Take the cube root (since there are 3 numbers): ∛64 ≈ 4

The geometric mean of 2, 4, and 8 is 4. This result tells us that if we had three equal numbers, each equal to 4, their product would be the same as the product of the original numbers. Essentially, 4 is the consistent growth factor across all three values.

Calculating the geometric mean by adding logarithms

For larger datasets or to avoid overflow errors when dealing with very large numbers, we can use logarithms. This method simplifies multiplication into addition and makes calculations more manageable. Here, we first take the logarithm of each number, calculate the arithmetic mean of these logarithms, and then take the antilog (exponential) of this mean. Let’s use the same example as above. 

1. Take logarithms (base 10): log(2) ≈ 0.3010, log(4) ≈ 0.6021, log(8) ≈ 0.9031
2. Calculate the arithmetic mean: (0.3010 + 0.6021 + 0.9031) / 3 ≈ 0.6021
3. Take the antilog: (10^x) = 10^0.6021 ≈ 4

This method gives us the same result as the direct calculation method. You can use logarithms of any base (such as natural logarithms with base e), as long as you use the same base throughout the calculation. The final geometric mean will be the same.

Geometric Mean in Data Science and Machine Learning

The geometric mean is a useful statistical measure with several important applications in data science and machine learning. Here are three key use cases where the geometric mean proves valuable. 

Growth rates and time series analysis

In data science, we often analyze growth rates over time, such as in population dynamics, market trends, or user adoption rates. The geometric mean is ideal for these situations because it accurately captures the compounding nature of growth. Unlike the arithmetic mean, which simply averages the rates without considering how each year's growth builds upon the last, the geometric mean accounts for this compounding effect.

Imagine you're analyzing the annual growth rate of a startup's user base over five years: 20%, 15%, 25%, 10%, and 30%. While the arithmetic mean (20%) might seem like a quick solution, it doesn't account for the compounding effect. The geometric mean ((1.20 * 1.15 * 1.25 * 1.10 * 1.30)^(1/5) - 1 ≈ 19.77%) provides a more accurate average growth rate that, if applied consistently each year, would result in the same final value as the actual varied growth rates.

Statistical analysis of skewed data

In data science, we often deal with datasets that are positively skewed due to multiplicative processes, such as income levels, biological measurements, or certain financial indicators. In such cases, using the arithmetic mean can be misleading because it is sensitive to extreme values (outliers), which can distort the representation of the central tendency.

The geometric mean is particularly useful when dealing with data that follow a log-normal distribution. Here's why:

• Minimizes the Influence of Outliers: The geometric mean reduces the impact of extremely high or low values, providing a more representative central value for skewed data.
• Handles Multiplicative Relationships: It is appropriate for data where values are combined multiplicatively rather than additively.

Consider a dataset of household incomes in a region where most households earn between $30,000 and $60,000, but a few earn over $1 million.

• Arithmetic Mean Income: This will be heavily influenced by the high-income outliers, potentially suggesting an average income much higher than what most people earn.
• Geometric Mean Income: This provides a central value that reflects the typical income more accurately by minimizing the influence of the extreme values.

By using the geometric mean in such cases, data scientists can obtain a more accurate measure of central tendency, leading to better insights and more reliable analyses. This makes the geometric mean an essential tool when working with skewed data distributions in various fields.

Evaluation metrics for imbalanced datasets

In classification tasks, we often encounter imbalanced datasets where some groups are represented by a much larger number of examples than others. In such cases, traditional evaluation metrics like accuracy can be misleading. This is where the Geometric Mean Score, or G-Mean, becomes a valuable tool.

The G-Mean is the root of the product of class-wise sensitivity (recall). For binary classification, it's the square root of the product of sensitivity and specificity. For multi-class problems, it's a higher root of the product of sensitivity for each class.

G-Mean aims to balance accuracy across all classes, making it particularly useful for imbalanced datasets. However, it's important to note that G-Mean is undefined when any class has zero sensitivity, limiting its applicability in extreme imbalance scenarios. In practice, modified versions or alternative metrics may be used to address this limitation.

To see more how the geometric mean and other statistical measures are applied in machine learning, consider exploring our Machine Learning Scientist with Python career track, which offers in-depth lesson that cover essential machine learning concepts and techniques, with practical insights and hands-on experience.