Média aritmética: Uma ferramenta fundamental para a análise de dados

A média aritmética, comumente conhecida como "a média", costuma ser o ponto de partida nas estatísticas descritivas. Ele fornece uma medida rápida e intuitiva da tendência central, que é uma parte essencial da interpretação de dados em qualquer campo. Embora o conceito possa parecer simples, a compreensão das nuances da média aritmética pode revelar insights reais sobre tendências e padrões de dados mais complexos.

Este artigo oferece uma visão geral da média aritmética, abordando sua fórmula, aplicações e comparações com outros tipos de média. Examinaremos por que ele é usado com frequência na economia, na ciência de dados e em outras áreas, além de discutir cenários em que medidas alternativas podem ser mais adequadas.

Para os iniciantes em estatística ou para aqueles que desejam solidificar seus conhecimentos, nosso curso de Introdução à Estatística oferece uma excelente base. Nossa Folha de consulta de estatísticas descritivas também fornece um glossário útil de termos relacionados a esse tópico.

O que é a média aritmética?

A média aritmética é a soma de todos os números em um conjunto de dados dividida pela contagem desses números. Esse cálculo simples o torna uma das medidas de tendência central mais intuitivas e amplamente utilizadas.

Para ilustrar, vamos considerar um exemplo simples. Suponha que você tenha três números: 5, 10 e 15. Para calcular sua média aritmética:

1. Some os números: 5 + 10 + 15 = 30
2. Conte os números: Temos 3 números
3. Divida a soma pela contagem: 30 ÷ 3 = 10

Portanto, a média aritmética de 5, 10 e 15 é 10.

Principais propriedades da média aritmética

A média aritmética possui várias propriedades importantes que se tornam mais intrigantes quando você as examina mais de perto. 

A soma dos desvios é igual a zero

Uma propriedade fundamental da média aritmética é que a soma dos desvios dela é sempre igual a zero. Em outras palavras, se você subtrair o valor médio de cada ponto de dados e somar essas diferenças, o resultado será zero. Matematicamente, isso pode ser expresso como:

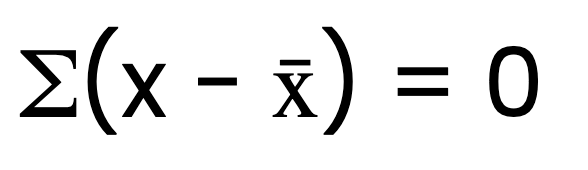
Onde x representa cada valor no conjunto de dados, e x̄ é a média aritmética.

Sensibilidade a valores discrepantes

Em conjuntos de dados com valores extremos, a média aritmética pode ser puxada significativamente em direção a esses valores discrepantes, o que pode levar a interpretações enganosas, especialmente em distribuições distorcidas. Por exemplo, considere um conjunto de dados de salários em uma pequena empresa: {$30,000, $35,000, $40,000, $45,000, $1,000,000}. A média aritmética (US$ 230.000) é significativamente mais alta do que a maioria dos salários devido ao valor discrepante de US$ 1.000.000.

Essa sensibilidade torna a média aritmética menos robusta do que medidas como a mediana na presença de valores discrepantes ou para distribuições distorcidas. No entanto, isso também pode tornar a média útil para detectar a presença de valores discrepantes ou entender o impacto de valores extremos em um conjunto de dados.

Impacto das mudanças nos dados

A média aritmética responde de forma previsível às mudanças no conjunto de dados, o que pode ser útil em vários cenários analíticos:

1. Adição ou subtração de uma constante: Se você adicionar ou subtrair o mesmo valor de cada ponto de dados, a média aumentará ou diminuirá exatamente nesse valor. Por exemplo, se você adicionar 5 a cada valor em um conjunto de dados, a nova média será 5 a mais do que a média original.
2. Multiplicando ou dividindo por uma constante: Se você multiplicar ou dividir cada ponto de dados pela mesma constante diferente de zero, a média será multiplicada ou dividida por essa constante. Por exemplo, se você duplicar cada valor em um conjunto de dados, a nova média será o dobro da média original.

Essas propriedades tornam a média aritmética particularmente útil em cenários que envolvem alterações uniformes em um conjunto de dados, como o ajuste da inflação em dados econômicos ou medições de escala em experimentos científicos.

Quando usar a média aritmética

A média aritmética é uma ferramenta estatística versátil, mas é particularmente eficaz em determinados cenários. Em primeiro lugar, devemos dizer que a média aritmética do é particularmente útil para conjuntos de dados que envolvem processos aditivos. Por exemplo, se você estiver calculando a temperatura média diária, o salário médio em uma empresa ou a pontuação média em um teste, a média aritmética fornecerá uma representação significativa do valor central.

Além disso, devemos dizer que a média aritmética é é mais confiável quando os pontos de dados são distribuídos uniformemente e não há valores extremos discrepantes. Vamos dar uma olhada em alguns exemplos específicos do setor:

• Finanças: No setor financeiro, as empresas se baseiam na média aritmética para obter insights e definir padrões de referência. Por exemplo, as empresas o utilizam para determinar salários médios, despesas mensais e lucros trimestrais.
• Economia: Os economistas usam a média aritmética para analisar as tendências de consumo e a estabilidade de preços. As principais aplicações incluem o cálculo do consumo médio das famílias e a criação de índices como o Índice de Preços ao Consumidor (IPC) para monitorar a inflação ao longo do tempo.
• Cuidados com a saúde e pesquisa médica: Na área da saúde, a média aritmética desempenha um papel fundamental na avaliação de tratamentos e no estudo de tendências de saúde. Por exemplo, os pesquisadores calculam os tempos médios de recuperação e a eficácia dos medicamentos, enquanto os epidemiologistas avaliam as taxas médias de infecção e os tempos de sobrevivência.

Como calcular a média aritmética

Embora já tenhamos abordado o conceito básico, vamos explorar como calcular a média aritmética usando ferramentas como R, Python e Excel, o que é praticamente necessário para conjuntos de dados maiores.

Fórmula da média aritmética

A fórmula para a média aritmética é:

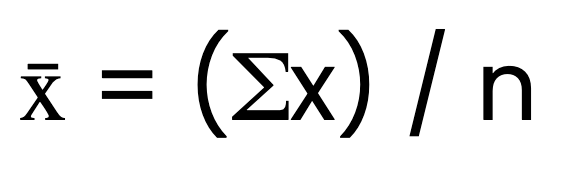
Em que x̄ é a média aritmética, Σx é a soma de todos os valores e n é o número de valores.

Média aritmética no Excel, Python e R

Para conjuntos de dados maiores, as ferramentas de software facilitam muito a computação. Veja como você pode calcular a média aritmética no Excel, Python e R. 

Excel

No Excel, você pode usar a função AVERAGE():

1. Insira seus dados em uma coluna ou linha.

2. Em uma nova célula, digite =AVERAGE().

3. Selecione o intervalo de células que contém seus dados.

4. Feche o parêntese e pressione Enter.

Por exemplo, se seus dados estiverem nas células A1:A10, você usaria: =AVERAGE(A1:A10).

Python

O módulo de estatísticas do Python fornece uma função mean():

from statistics import mean

data = [5, 10, 15, 20, 25]

result = mean(data)
print(result)  # Output: 15

Para conjuntos de dados maiores, você pode preferir a função mean() do NumPy, que é mais eficiente:

import numpy as np

data = np.array([5, 10, 15])

result = np.mean(data)
print(result)  # Output: 10.0

R

No R, você pode usar a função integrada mean() do R básico:

data <- c(5, 10, 15)

result <- mean(data)
print(result)  # Output: [1] 10

Essas ferramentas simplificam o processo de cálculo da média aritmética para conjuntos de dados de qualquer tamanho, permitindo que você se concentre na interpretação dos dados em vez de fazer cálculos manuais.

Média aritmética em ciência de dados, aprendizado de máquina e estatística

As aplicações da média aritmética na ciência de dados e no aprendizado de máquina abrangem desde o pré-processamento de dados até a avaliação do modelo. Vamos explorar algumas áreas-chave em que a média aritmética é particularmente importante. 

Dimensionamento de recursos

Uma das aplicações mais comuns da média aritmética no pré-processamento de dados é o dimensionamento de recursos, especialmente na centralização da média:

• Centralização média: Esse processo envolve a subtração da média aritmética de cada ponto de dados em um recurso. O resultado é um conjunto de dados centralizado em que a média de cada recurso é zero. Isso pode ser representado como: x_centered = x - x̄ onde x é o valor original e x̄ é a média aritmética do recurso.

• Padronização: Frequentemente usada em conjunto com a centralização da média, a padronização envolve a divisão pelo desvio padrão após a subtração da média: x_standardized = (x - x̄) / σ, em que σ é o desvio padrão do recurso.

Essas técnicas ajudam a normalizar a escala dos recursos, o que é particularmente importante para muitos algoritmos de aprendizado de máquina. Se quiser saber mais sobre a diferença entre normalização e padronização, você pode explorar o tutorial abrangente.

Avaliação do modelo

A média aritmética é fundamental em várias métricas de avaliação de modelos:

• Erro quadrático médio (MSE): Essa métrica comum para problemas de regressão calcula a média das diferenças quadráticas entre os valores previstos e reais.
• Erro Absoluto Médio (MAE): Semelhante ao MSE, mas usa a diferença absoluta em vez da diferença ao quadrado.
• Precisão: Em problemas de classificação, a precisão é geralmente relatada como a média de previsões corretas em todas as amostras.

Estatísticas e testes de hipóteses

Na análise estatística, a média aritmética é frequentemente usada em testes de hipóteses. Por exemplo:

• Testes T: A média aritmética é fundamental nos testes t, que comparam as médias de dois grupos para determinar se são estatisticamente diferentes. Ao comparar as médias das amostras, os testes t ajudam a validar as hipóteses sobre as características da população.
• Intervalos de confiança: A média aritmética é usada para calcular os intervalos de confiança, que indicam a confiabilidade da média estimada. Isso dá uma ideia de como a média da amostra é representativa de toda a população.

Outros aplicativos

• Métodos de conjunto: Muitas técnicas de conjunto, como bagging e boosting, usam a média aritmética para combinar previsões de vários modelos.
• Descida de gradiente: A média aritmética é usada para calcular o gradiente médio entre os minilotes na descida de gradiente estocástica.
• Detecção de anomalias: Os desvios da média podem ser usados para identificar exceções ou anomalias em conjuntos de dados. Por exemplo, uma heurística comum é usar três desvios padrão como limite, de modo que qualquer ponto de dados que esteja a três ou mais desvios padrão da média aritmética seria considerado um outlier.
• Redução de dimensionalidade: Técnicas como a análise de componentes principais (PCA) usam a média aritmética em seus cálculos para centralizar os dados antes de calcular a matriz de covariância.
• Redes neurais: No algoritmo de retropropagação, a média aritmética é usada para calcular o erro médio nos exemplos de treinamento.
• Validação cruzada: Ao realizar a validação cruzada k-fold, a média aritmética das métricas de desempenho em todas as dobras é normalmente relatada como a estimativa geral de desempenho.

Como você deve ter percebido, a média aritmética é importante para interpretar a saída dos dados e, muitas vezes, também é importante como uma etapa de pré-processamento necessária para o desempenho ideal do modelo. Para aprofundar sua compreensão desses conceitos e de suas aplicações práticas, considere fazer nosso curso de carreira de Cientista de Aprendizado de Máquina em Python, que aborda esses tópicos com mais profundidade.