Arithmetic Mean: A Foundational Tool for Data Analysis

The arithmetic mean, commonly known as "the average," is often the starting point in descriptive statistics. It provides a quick, intuitive measure of central tendency, which is an essential part of interpreting data in any field. While the concept may seem straightforward, understanding the arithmetic mean's nuances can reveal real insights into more complex data trends and patterns.

This article offers an overview of the arithmetic mean, covering its formula, applications, and comparisons with other types of means. We'll examine why it's frequently used in economics, data science, and beyond, while also discussing scenarios where alternative measures might be more suitable.

For those new to statistics or looking to solidify their understanding, our Introduction to Statistics course provides a great foundation. Our Descriptive Statistics Cheat Sheet also provides a helpful glossary of terms related to this topic.

What is the Arithmetic Mean?

The arithmetic mean is the sum of all numbers in a dataset divided by the count of those numbers. This straightforward calculation makes it one of the most intuitive and widely used measures of central tendency.

To illustrate, let's consider a simple example. Suppose we have three numbers: 5, 10, and 15. To calculate their arithmetic mean:

1. Sum the numbers: 5 + 10 + 15 = 30
2. Count the numbers: We have 3 numbers
3. Divide the sum by the count: 30 ÷ 3 = 10

Thus, the arithmetic mean of 5, 10, and 15 is 10.

Key Properties of the Arithmetic Mean

The arithmetic mean possesses several important properties that become more intriguing upon closer examination. 

Summing deviations equals zero

A fundamental property of the arithmetic mean is that the sum of deviations from it always equals zero. In other words, if you subtract the mean value from each data point and sum these differences, the result will be zero. Mathematically, this can be expressed as:

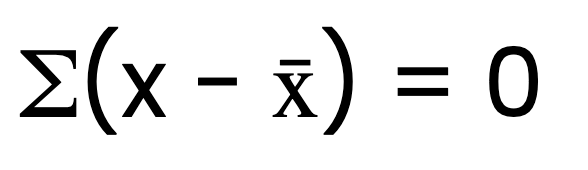
Where x represents each value in the dataset, and x̄ is the arithmetic mean.

Sensitivity to outliers

In datasets with extreme values, the arithmetic mean can be pulled significantly towards these outliers, potentially leading to misleading interpretations, especially in skewed distributions. For example, consider a dataset of salaries in a small company: {$30,000, $35,000, $40,000, $45,000, $1,000,000}. The arithmetic mean ($230,000) is significantly higher than most salaries due to the outlier of $1,000,000.

This sensitivity makes the arithmetic mean less robust than measures like the median in the presence of outliers or for skewed distributions. However, it can also make the mean useful for detecting the presence of outliers or understanding the impact of extreme values on a dataset.

Impact of changes in data

The arithmetic mean responds predictably to changes in the dataset, which can be useful in various analytical scenarios:

1. Adding or Subtracting a Constant: If you add or subtract the same value from every data point, the mean will increase or decrease by that exact amount. For instance, if you add 5 to each value in a dataset, the new mean will be 5 more than the original mean.
2. Multiplying or Dividing by a Constant: If you multiply or divide every data point by the same non-zero constant, the mean will be multiplied or divided by that constant. For example, if you double every value in a dataset, the new mean will be twice the original mean.

These properties make the arithmetic mean particularly useful in scenarios involving uniform changes across a dataset, such as adjusting for inflation in economic data or scaling measurements in scientific experiments.

When to Use the Arithmetic Mean

The arithmetic mean is a versatile statistical tool, but it's particularly effective in certain scenarios. We should first say that the arithmetic mean is particularly useful for datasets involving additive processes. For instance, if you're calculating average daily temperature, average salary in a company, or average test scores, the arithmetic mean provides a meaningful representation of the central value.

Also, we should say that the arithmetic mean is most reliable when data points are evenly distributed, and there are no extreme outliers. Let's take a look at some industry-specific examples:

• Finance: In finance, companies rely on the arithmetic mean to gain insights and set benchmarks. For example, businesses use it to determine average salaries, monthly expenses, and quarterly profits.
• Economics: Economists use the arithmetic mean to analyze consumer trends and price stability. Key applications include calculating average household consumption and building indices like the Consumer Price Index (CPI) to monitor inflation over time.
• Healthcare and Medical Research: In healthcare, the arithmetic mean plays a critical role in evaluating treatments and studying health trends. For instance, researchers calculate average recovery times and drug efficacy, while epidemiologists assess average infection rates and survival times.

How to Calculate the Arithmetic Mean

While we've already covered the basic concept, let's explore how to calculate the arithmetic mean using tools like R, Python, and Excel, which is practically necessary for larger datasets.

Arithmetic mean formula

The formula for the arithmetic mean is:

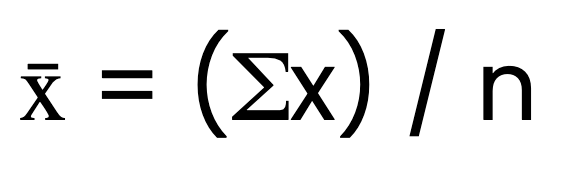
Where x̄ is the arithmetic mean, Σx is the sum of all values, and n is the number of values.

Arithmetic mean in Excel, Python, and R

For larger datasets, software tools make computation much easier. Here's how to calculate the arithmetic mean in Excel, Python, and R. 

Excel

In Excel, you can use the AVERAGE() function:

1. Enter your data into a column or row.

2. In a new cell, type =AVERAGE().

3. Select the range of cells containing your data.

4. Close the parenthesis and press Enter.

For example, if your data is in cells A1:A10, you would use: =AVERAGE(A1:A10).

Python

Python's statistics module provides a mean() function:

from statistics import mean

data = [5, 10, 15, 20, 25]

result = mean(data)
print(result)  # Output: 15

For larger datasets, you might prefer NumPy's more efficient mean() function:

import numpy as np

data = np.array([5, 10, 15])

result = np.mean(data)
print(result)  # Output: 10.0

R

In R, you can use the built-in mean() function from base R:

data <- c(5, 10, 15)

result <- mean(data)
print(result)  # Output: [1] 10

These tools streamline the process of calculating the arithmetic mean for datasets of any size, allowing you to focus on data interpretation rather than manual computation.

Arithmetic Mean in Data Science, Machine Learning, and Statistics

The applications of the arithmetic mean in data science and machine learning span from data preprocessing to model evaluation. Let's explore some key areas where the arithmetic mean is particularly important. 

Feature scaling

One of the most common applications of the arithmetic mean in data preprocessing is feature scaling, particularly in mean centering:

• Mean Centering: This process involves subtracting the arithmetic mean from each data point in a feature. The result is a centered dataset where the mean of each feature is zero. This can be represented as: x_centered = x - x̄ where x is the original value and x̄ is the arithmetic mean of the feature.

• Standardization: Often used in conjunction with mean centering, standardization involves dividing by the standard deviation after subtracting the mean: x_standardized = (x - x̄) / σ, where σ is the standard deviation of the feature.

These techniques help in normalizing the scale of features, which is particularly important for many machine learning algorithms. If you want to learn more about the difference between normalization and standardization, you can explore the comprehensive tutorial.

Model evaluation

The arithmetic mean is fundamental in various model evaluation metrics:

• Mean Squared Error (MSE): This common metric for regression problems calculates the average of the squared differences between predicted and actual values.
• Mean Absolute Error (MAE): Similar to MSE, but uses the absolute difference instead of squared difference.
• Accuracy: In classification problems, accuracy is often reported as the mean of correct predictions across all samples.

Statistics and hypothesis testing

In statistical analysis, the arithmetic mean is often used in hypothesis testing. For example:

• T-Tests: The arithmetic mean is crucial in t-tests, which compare the means of two groups to determine if they are statistically different. By comparing sample means, t-tests help validate hypotheses about population characteristics.
• Confidence Intervals: The arithmetic mean is used to calculate confidence intervals, which indicate the reliability of the estimated mean. This gives insight into how representative the sample mean is for the entire population.

Other applications

• Ensemble Methods: Many ensemble techniques, such as bagging and boosting, use the arithmetic mean to combine predictions from multiple models.
• Gradient Descent: The arithmetic mean is used in calculating the average gradient across mini-batches in stochastic gradient descent.
• Anomaly Detection: Deviations from the mean can be used to identify outliers or anomalies in datasets. For example, one common heuristic is to use three standard deviations as a threshold, so any data point that is three or more standard deviations away from the arithmetic mean would be considered an outlier.
• Dimensionality Reduction: Techniques like principal component analysis (PCA) use the arithmetic mean in their calculations to center the data before computing the covariance matrix.
• Neural Networks: In the backpropagation algorithm, the arithmetic mean is used to calculate the average error across training examples.
• Cross-Validation: When performing k-fold cross-validation, the arithmetic mean of the performance metrics across all folds is typically reported as the overall performance estimate.

As you might be noticing, the arithmetic mean is important both for interpreting the output of the data and it’s often also important as a preprocessing step that is necessary for optimal model performance. To deepen your understanding of these concepts and their practical applications, consider taking our Machine Learning Scientist in Python career track, which covers these topics in greater depth.