Quadratwurzel in Excel: Eine kurze Lektion

Excel bietet dir mit der Funktion SQRT() eine einfache Möglichkeit, Quadratwurzeln zu berechnen. Es ist eine schnelle, integrierte Methode, die gut für positive Zahlen funktioniert und sich leicht in andere Formeln integrieren lässt.

In diesem Artikel erkläre ich dir, wie du die Funktion SQRT() in Excel verwendest und zeige dir, worauf du achten musst, einschließlich Fehler und alternative Methoden wie POWER().

Excel SQRT() verstehen

Die Funktion SQRT() in Excel ist ein einfaches Werkzeug, das die positive Quadratwurzel aus einer Zahl liefert. Wenn du den Wert finden musst, der, wenn du ihn mit dir selbst multiplizierst, die ursprüngliche Zahl ergibt, erledigt das SQRT() für dich. Die Quadratwurzel aus 16 ist zum Beispiel 4, denn 4 × 4 = 16.

Du wirst SQRT() in allen möglichen Situationen nützlich finden. Bevor wir uns Beispiele ansehen, wollen wir uns ansehen, wie SQRT() funktioniert.

Wie funktioniert SQRT()?

Hier ist die Syntax für die Funktion:

=SQRT(number)

Ersetze number durch den Wert oder den Zellbezug, aus dem du die Quadratwurzel ziehen willst.

Wann solltest du SQRT() verwenden?

Wann ist SQRT() also das richtige Werkzeug für den Job? Immer wenn du die positive Quadratwurzel einer positiven Zahl finden musst, funktioniert diese Funktion. Sie wird häufig in der Geometrie (z.B. um die Seitenlänge eines Quadrats mit seiner Fläche zu bestimmen), in der Statistik und sogar im Finanzwesen verwendet. Wie wir in den nächsten Beispielen sehen werden, kommen diese Anwendungsfälle häufiger vor, als du vielleicht denkst.

Einige SQRT()-Beispiele

Wir wollen uns nun ein paar grundlegende Beispiele ansehen, die zeigen, wie SQRT() in verschiedenen Situationen funktioniert.

Die Quadratwurzel aus einer Zahl ziehen

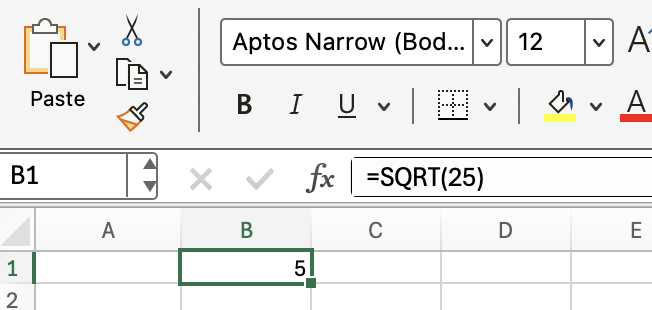
Schauen wir uns zunächst die direkteste Anwendung an: die Berechnung der Quadratwurzel aus einer bestimmten Zahl. Wenn du die Quadratwurzel aus 25 willst, gibst du dies in eine beliebige Zelle ein:

=SQRT(25)

Excel wird 5 zurückgeben. Diese einfache Berechnung legt den Grundstein für dynamischere Anwendungen.

Einen Zellbezug verwenden

In Anlehnung an unser vorheriges Beispiel wirst du wahrscheinlich nicht immer Zahlen fest codieren. Wenn Zelle A1 eine Zahl enthält, z. B. 81, verwende:

=SQRT(A1)

Das ergibt 9, denn 9 × 9 = 81.

Das Referenzieren von Zellen macht deine Formeln flexibel und dynamisch, was besonders nützlich ist, wenn du mit wechselnden Daten arbeitest.

SQRT() mit Formeln

Wenn du einen Schritt weiter gehst, kannst du Berechnungen innerhalb von SQRT() verwenden. Um zum Beispiel die Quadratwurzel aus der Summe der Werte in A1 und B1 zu erhalten:

=SQRT(A1 + B1)

Dies ist besonders praktisch, wenn du mit dynamischen Daten arbeitest, die mehrere Eingaben kombinieren.

SQRT() und negative Zahlen

SQRT() ist einfach und effektiv, aber du kannst trotzdem Fehler machen. Die erste und wichtigste Einschränkung ist, dass SQRT() nicht mit negativen Zahlen umgehen kann. Wenn du es versuchst:

=SQRT(-9)

Excel gibt einen #NUM! Fehler zurück. Das liegt daran, dass die Quadratwurzel einer negativen Zahl keine reale Zahl ist - sie ist imaginär.

Jetzt fragst du dich vielleicht, wie du deine Formeln so gestalten kannst, dass sie nicht fehlschlagen, wenn sie auf eine negative Eingabe treffen. Die Lösung ist, SQRT() in eine IF() Anweisung zu verpacken, um das Problem abzufangen:

=IF(A1 < 0, "Invalid", SQRT(A1))

Diese Formel zeigt "Ungültig" an, wenn A1 negativ ist; andernfalls liefert sie die Quadratwurzel.

Verwendung von SQRT() in realen Szenarien

Sehen wir uns an, wie SQRT() in der realen Welt angewendet wird.

Geometry: Berechnen der Diagonale eines Quadrats

Angenommen, du kennst die Seitenlänge eines Quadrats in Zelle A1 und möchtest die Diagonale ermitteln. Die Formel für die Diagonale d eines Quadrats lautet: d = Seite × SQRT(2)

Verwende in Excel:

=A1 * SQRT(2)

So erhältst du die diagonale Länge auf der Grundlage der Seite in A1.

Statistik: Berechnung der Standardabweichung

Versuchen wir es mal mit etwas aus der Statistik. Wenn du die Abweichung in Zelle B1 bereits berechnet hast,

=SQRT(B1)

gibt dir die Standardabweichung an.

Während die in Excel eingebauten Funktionen STDEV.P() oder STDEV.S() oft bequemer sind, kann das Verständnis dafür, wie SQRT() in statistische Berechnungen passt, helfen, zu verstehen, was passiert.

Verwandte Funktionen

Vielleicht brauchst du verwandte Funktionen, die ähnliche oder komplexere Berechnungen durchführen. Ich möchte dir ein paar solcher Tools vorstellen.

• POWER() kannst du eine Zahl auf einen beliebigen Exponenten erhöhen (einschließlich 0,5 für Quadratwurzeln).

• ABS() erhält den absoluten Wert einer Zahl.

• STDEV.P() und STDEV.S() die Standardabweichung ohne manuelle SQRT() Schritte behandeln.

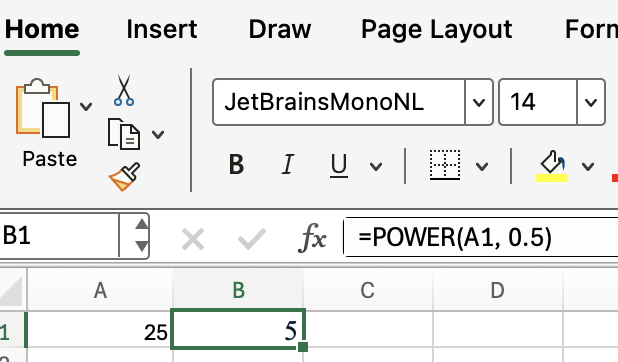
Zum Beispiel, um die Quadratwurzel mit POWER() zu erhalten:

=POWER(A1, 0.5) 

Diese Methode macht das Gleiche wie SQRT(A1). Wenn du also nur an Quadratwurzeln interessiert bist, hat diese Methode keinen Vorteil. Aber POWER() kann mit jedem Exponenten umgehen. Wenn du also auch mit Kubikwurzeln oder gebrochenen Exponenten arbeitest, solltest du POWER() ebenfalls kennen.

Fehlersuche bei SQRT()

Zum Schluss noch ein paar Tipps zur Fehlerbehebung, die dir helfen, häufige Fehler zu vermeiden.

• Wenn du eine negative Zahl eingibst, erhältst du immer die Fehlermeldung #NUM!.

• SQRT() ignoriert Text und leere Zellen; wenn du dich auf eine Zelle mit Text oder Leerzeichen beziehst, gibt sie #VALUE! zurück.

• Wenn deine Zahl Null ist, gibt SQRT(0) einfach Null zurück.

Wenn du mit negativen Zahlen umgehen musst (z. B. wenn du die komplexe Quadratwurzel berechnen willst), kann Excel das nicht von Haus aus, ohne die Funktionen IMAGINARY() und COMPLEX() zu verwenden. Dies ist eine gute Erinnerung daran, dass SQRT() zwar die meisten Anwendungsfälle abdeckt, spezielle Szenarien jedoch einen anderen Ansatz erfordern können.

Fazit

Wenn du deine Excel- (und Mathe-)Kenntnisse vertiefen möchtest, solltest du dich mit verwandten Funktionen wie POWER(), IMAGINARY(), COMPLEX() und ABS() beschäftigen.

Und natürlich gibt es keinen Ersatz für strukturiertes Lernen, also melde dich für unseren Lernpfad Excel-Grundlagen und unseren Kurs Excel-Funktionen für Fortgeschrittene an.