Racine carrée dans Excel : Une leçon rapide

Excel vous offre un moyen simple de calculer les racines carrées à l'aide de la fonction SQRT(). Il s'agit d'une méthode rapide et intégrée qui fonctionne bien pour les nombres positifs et qui s'intègre facilement dans d'autres formules.

Dans cet article, je vous expliquerai comment utiliser la fonction SQRT() dans Excel et je vous montrerai ce à quoi il faut faire attention, y compris les erreurs et les méthodes alternatives comme POWER().

Comprendre Excel SQRT()

La fonction SQRT() d'Excel est un outil simple qui renvoie la racine carrée positive d'un nombre. Si vous devez trouver la valeur qui, une fois multipliée par elle-même, vous donne le nombre original, SQRT() s'en charge pour vous. Par exemple, la racine carrée de 16 est 4, car 4 × 4 = 16.

Vous trouverez certainement SQRT() utile dans toutes sortes de scénarios. Avant d'examiner des exemples, voyons comment fonctionne SQRT().

Comment fonctionne SQRT() ?

Voici la syntaxe de la fonction :

=SQRT(number)

Remplacez number par la valeur ou la référence de cellule dont vous souhaitez obtenir la racine carrée.

Quand devez-vous utiliser SQRT() ?

Alors, quand SQRT() est-il le bon outil pour le travail ? Chaque fois que vous devez trouver la racine carrée positive d'un nombre positif, cette fonction fonctionne. Elle est courante en géométrie (par exemple pour trouver la longueur du côté d'un carré en fonction de sa surface), en statistique et même en finance. Comme nous le verrons dans les exemples suivants, ces cas d'utilisation sont plus fréquents que vous ne le pensez.

Quelques exemples de SQRT()

Nous allons maintenant explorer quelques exemples de base qui montrent comment SQRT() fonctionne dans une variété de situations.

Trouver la racine carrée d'un nombre

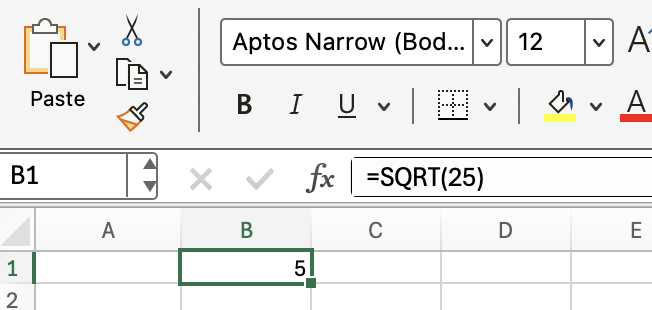
Commençons par l'utilisation la plus directe : le calcul de la racine carrée d'un nombre spécifique. Si vous voulez la racine carrée de 25, tapez ceci dans n'importe quelle cellule :

=SQRT(25)

Excel renvoie 5. Ce simple calcul jette les bases d'applications plus dynamiques.

Utilisation d'une référence de cellule

Dans le prolongement de l'exemple précédent, vous ne coderez probablement pas toujours les chiffres en dur. Si la cellule A1 contient un nombre, comme 81, utilisez :

=SQRT(A1)

Vous obtiendrez 9, puisque 9 × 9 = 81.

Le référencement des cellules rend vos formules flexibles et dynamiques, ce qui est particulièrement utile lorsque vous travaillez avec des données changeantes.

SQRT() avec formules

Pour aller plus loin, vous pouvez utiliser des calculs à l'intérieur de SQRT(). Par exemple, pour obtenir la racine carrée de la somme des valeurs de A1 et B1 :

=SQRT(A1 + B1)

Cela s'avère utile lorsque vous travaillez avec des données dynamiques qui combinent plusieurs entrées.

SQRT() et les nombres négatifs

SQRT() est simple et efficace, mais vous pouvez toujours commettre des erreurs. La première limitation, et la plus importante, est que SQRT() ne peut pas gérer les nombres négatifs. Si vous essayez :

=SQRT(-9)

Excel renvoie une erreur #NUM!. En effet, la racine carrée d'un nombre négatif n'est pas un nombre réel, c'est un nombre imaginaire.

Vous vous demandez peut-être comment concevoir vos formules de manière à ce qu'elles n'échouent pas en cas d'entrée négative. La solution consiste à envelopper SQRT() dans une déclaration IF() pour détecter le problème :

=IF(A1 < 0, "Invalid", SQRT(A1))

Cette formule affichera "Invalide" si A1 est négatif ; sinon, elle renverra la racine carrée.

Utilisation de SQRT() dans des scénarios réels

Voyons comment SQRT() s'applique dans des contextes réels.

Géométrie : Calculer la diagonale d'un carré

Supposons que vous connaissiez la longueur du côté d'un carré dans la cellule A1 et que vous souhaitiez trouver la diagonale. La formule de la diagonale d d 'un carré est la suivante : d = côté × SQRT(2)

Dans Excel, utilisez :

=A1 * SQRT(2)

Vous obtenez ainsi la longueur de la diagonale en fonction du côté en A1.

Statistiques : Calcul de l'écart-type

Essayons quelque chose du côté des statistiques. Si vous avez déjà calculé la variance dans la cellule B1,

=SQRT(B1)

vous donne l'écart-type.

Wien que les fonctions intégrées STDEV.P() ou STDEV.S() d'Excel soient souvent plus pratiques, comprendre comment SQRT() s'intègre dans les calculs statistiques peut aider à clarifier ce qui se passe.

Fonctions connexes

Il se peut que vous ayez besoin de fonctions connexes pour effectuer des calculs similaires ou plus complexes. Permettez-moi de vous présenter quelques-uns de ces outils.

• POWER() vous permet d'élever un nombre à n'importe quel exposant (y compris 0,5 pour les racines carrées).

• ABS() obtient la valeur absolue d'un nombre.

• STDEV.P() et STDEV.S() traiter l'écart-type sans passer par les étapes manuelles de SQRT().

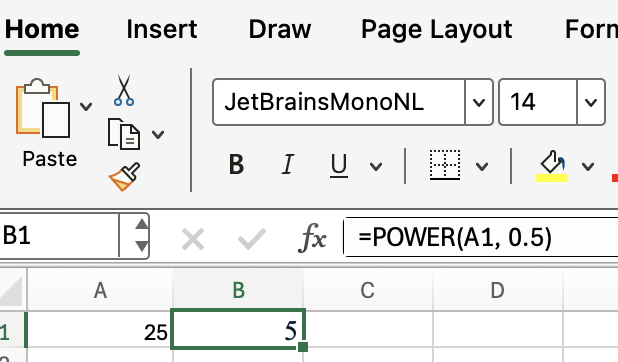
Par exemple, pour obtenir la racine carrée avec POWER():

=POWER(A1, 0.5) 

Cette méthode fait la même chose que SQRT(A1), et ne présente donc aucun avantage si vous n'êtes intéressé que par les racines carrées. Mais POWER() peut traiter n'importe quel exposant, donc si vous travaillez également avec des racines cubiques ou des exposants fractionnaires, POWER() mérite d'être connu.

Dépannage de SQRT()

Terminons par quelques conseils de dépannage et quelques bizarreries qui vous aideront à éviter les erreurs les plus courantes.

• Si vous entrez un nombre négatif, vous obtiendrez toujours une erreur #NUM!.

• SQRT() ignore le texte et les cellules vides ; si vous faites référence à une cellule contenant du texte ou des espaces vides, il renvoie #VALUE!.

• Si votre nombre est égal à zéro, SQRT(0) renvoie simplement zéro.

Si vous devez traiter des nombres négatifs (par exemple, si vous souhaitez obtenir la racine carrée complexe), Excel ne gère pas cela de manière native sans utiliser les fonctions IMAGINARY() et COMPLEX(). Il est bon de rappeler que si SQRT() couvre la plupart des cas d'utilisation, des scénarios spécialisés peuvent nécessiter une approche différente.

Conclusion

Si vous souhaitez renforcer vos compétences en Excel (et en mathématiques), explorez les fonctions connexes telles que POWER(), IMAGINARY(), COMPLEX(), et ABS().

Et bien sûr, rien ne remplace un apprentissage structuré, alors inscrivez-vous à notre parcours de compétences Excel Fundamentals et à notre cours Advanced Excel Functions.