Raiz quadrada no Excel: Uma lição rápida

O Excel oferece a você uma maneira simples de calcular raízes quadradas usando a função SQRT(). É um método rápido e incorporado que funciona bem para números positivos e se integra facilmente a outras fórmulas.

Neste artigo, explicarei a você como usar a função SQRT() no Excel e mostrarei o que deve ser observado, incluindo erros e métodos alternativos como POWER().

Entendendo o SQRT() do Excel

A função SQRT() no Excel é uma ferramenta simples que retorna a raiz quadrada positiva de um número. Se você precisar encontrar o valor que, quando multiplicado por ele mesmo, fornece o número original, o site SQRT() faz isso para você. Por exemplo, a raiz quadrada de 16 é 4, porque 4 × 4 = 16.

Você certamente achará o SQRT() útil em todos os tipos de cenários. Antes de vermos os exemplos, vamos explicar como funciona o SQRT().

Como funciona a função SQRT()?

Aqui está a sintaxe da função:

=SQRT(number)

Substitua number pelo valor ou referência de célula da qual você deseja obter a raiz quadrada.

Quando você deve usar SQRT()?

Então, quando o SQRT() é a ferramenta certa para o trabalho? Sempre que você precisar encontrar a raiz quadrada positiva de um número positivo, essa função funcionará. É comum em geometria (como encontrar o comprimento do lado de um quadrado considerando sua área), estatística e até mesmo finanças. Como veremos nos próximos exemplos, esses casos de uso aparecem com mais frequência do que você imagina.

Alguns exemplos de SQRT()

Vamos agora explorar alguns exemplos básicos que mostram como o SQRT() funciona em diversas situações.

Como encontrar a raiz quadrada de um número

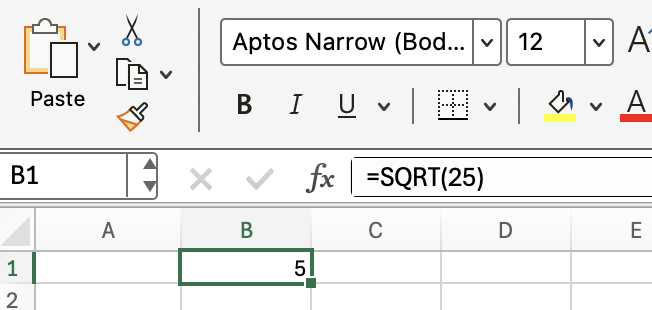
Para começar, vamos analisar o uso mais direto: calcular a raiz quadrada de um número específico. Se você quiser a raiz quadrada de 25, digite isso em qualquer célula:

=SQRT(25)

O Excel retornará 5. Esse cálculo simples estabelece a base para aplicativos mais dinâmicos.

Usando uma referência de célula

Com base em nosso exemplo anterior, você provavelmente nem sempre codificará números. Se a célula A1 contiver um número, como 81, use:

=SQRT(A1)

Isso dará a você 9, já que 9 × 9 = 81.

A referência a células torna suas fórmulas flexíveis e dinâmicas, o que é especialmente útil quando você trabalha com dados variáveis.

SQRT() com fórmulas

Indo um pouco além, você pode usar cálculos dentro do site SQRT(). Por exemplo, para obter a raiz quadrada da soma dos valores em A1 e B1, você deve usar a raiz quadrada:

=SQRT(A1 + B1)

Isso é útil quando você trabalha com dados dinâmicos que combinam várias entradas.

SQRT() e números negativos

SQRT() é simples e eficaz, mas você ainda pode cometer erros. A primeira e mais importante limitação é que o site SQRT() não consegue lidar com números negativos. Se você tentar:

=SQRT(-9)

O Excel retornará um erro #NUM!. Isso acontece porque a raiz quadrada de um número negativo não é um número real - é imaginário.

Agora você deve estar se perguntando como projetar suas fórmulas para que elas não falhem se encontrarem uma entrada negativa. A solução é envolver SQRT() em uma declaração IF() para detectar o problema:

=IF(A1 < 0, "Invalid", SQRT(A1))

Essa fórmula exibirá "Inválido" se A1 for negativo; caso contrário, ela retornará a raiz quadrada.

Usando SQRT() em cenários do mundo real

Vejamos como o SQRT() se aplica em contextos do mundo real.

Geometria: Calculando a diagonal de um quadrado

Suponha que você saiba o comprimento do lado de um quadrado na célula A1 e queira encontrar a diagonal. A fórmula para a diagonal d de um quadrado é: d = lado × SQRT(2)

No Excel, use:

=A1 * SQRT(2)

Isso dá a você o comprimento da diagonal com base no lado em A1.

Estatísticas: Cálculo do desvio padrão

Vamos tentar algo da estatística. Se você já tiver calculado a variância na célula B1,

=SQRT(B1)

fornece a você o desvio padrão.

Wmbora as funções STDEV.P() ou STDEV.S() incorporadas ao Excel sejam geralmente mais convenientes, entender como o SQRT() se encaixa nos cálculos estatísticos pode ajudar a esclarecer o que está acontecendo.

Funções relacionadas

Você pode precisar de funções relacionadas que manipulem cálculos semelhantes ou mais complexos. Vou apresentar algumas dessas ferramentas.

• POWER() permite que você aumente um número para qualquer expoente (incluindo 0,5 para raízes quadradas).

• ABS() obtém o valor absoluto de um número.

• STDEV.P() e STDEV.S() lidar com o desvio padrão sem etapas manuais SQRT().

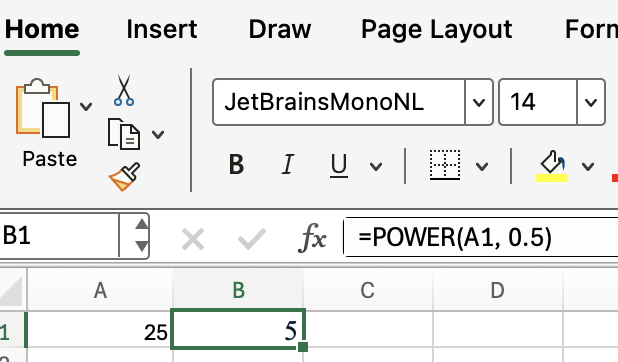
Por exemplo, para obter a raiz quadrada com POWER():

=POWER(A1, 0.5) 

Isso faz a mesma coisa que SQRT(A1), portanto, não há vantagem nesse método se você estiver interessado apenas em raízes quadradas. Mas o POWER() pode lidar com qualquer expoente, portanto, se você também estiver trabalhando com raízes cúbicas ou expoentes fracionários, também vale a pena conhecer o POWER().

Solução de problemas de SQRT()

Vamos encerrar com algumas dicas de solução de problemas e peculiaridades para ajudar você a evitar erros comuns.

• Se você inserir um número negativo, sempre receberá um erro #NUM!.

• SQRT() ignora texto e células vazias; se você fizer referência a uma célula com texto ou espaços em branco, ele retornará #VALUE!.

• Se o seu número for zero, SQRT(0) retornará zero.

Se você precisar lidar com números negativos (por exemplo, se quiser obter a raiz quadrada complexa), o Excel não lida com isso nativamente sem usar as funções IMAGINARY() e COMPLEX(). Esse é um bom lembrete de que, embora o site SQRT() cubra a maioria dos casos de uso, cenários especializados podem exigir uma abordagem diferente.

Conclusão

Se você deseja aprimorar suas habilidades em Excel (e matemática), explore funções relacionadas como POWER(), IMAGINARY(), COMPLEX() e ABS().

E, é claro, não há substituto para o aprendizado estruturado, portanto, inscreva-se em nosso programa de habilidades Fundamentos do Excel e em nosso curso Funções Avançadas do Excel.