Notação Big O e guia de complexidade de tempo: Intuição e matemática

A análise da complexidade do tempo oferece uma maneira de analisar e prever a eficiência dos algoritmos de forma independente da linguagem em que são implementados e do hardware em que são executados.

O objetivo da análise de complexidade de tempo não é prever o tempo exato de execução de um algoritmo, mas sim poder responder a essas perguntas:

1. Considerando dois algoritmos que resolvem o mesmo problema, qual deles deverá ser executado mais rapidamente se a mesma quantidade de dados for fornecida a ambos?
2. Se dobrássemos os dados fornecidos ao algoritmo, como o tempo de execução seria afetado? Ele será dimensionado linearmente e duplicado também? Você continuará o mesmo? Ou algo completamente diferente?

Ao final deste artigo, você saberá como analisar a complexidade de tempo de um algoritmo e responder a essas perguntas.

A complexidade do tempo ainda é importante em 2024?

Os computadores estão ficando cada vez mais rápidos, então você pode se perguntar se ainda há necessidade de se preocupar com a complexidade do tempo. Certamente, hoje em dia, um supercomputador pode lidar com qualquer problema, independentemente do algoritmo que usamos para resolvê-lo, certo?

Bem, não é bem assim. O boom da IA se deve, em grande parte, aos imensos avanços no desempenho do hardware nos últimos anos.  No entanto, mesmo no hardware mais avançado, problemas simples podem levar a um desempenho catastrófico se for usado um algoritmo lento.

Por exemplo, imagine que você use um algoritmo ingênuo para classificar uma tabela de banco de dados com dez milhões de entradas. Mesmo em um computador moderno, essa operação simples levaria vários dias para ser concluída, tornando o banco de dados inutilizável para qualquer aplicativo prático. Por outro lado, usando um algoritmo eficiente, podemos esperar que isso leve menos de um décimo de segundo.

Operações básicas e instruções básicas

Analisamos um algoritmo usando o modelo de máquina de acesso aleatório (RAM ou RA-machine). Esse modelo pressupõe que as operações a seguir levam exatamente uma etapa de tempo:

• Operações aritméticas
• Operações lógicas (<, >, ==, etc.)
• Declarações como if ou return
• Acesso a um local de memória, como gravação ou leitura de um valor variável

Essas operações são chamadas de operações básicas. Uma linha de código que executa um número constante de operações básicas é chamada deinstrução básica .

Como o número de operações em uma instrução básica é constante, ele não depende da quantidade de dados. Como nos preocupamos com o crescimento do tempo de execução à medida que a quantidade de dados aumenta, podemos nos concentrar em contar o número de instruções básicas que o algoritmo executa.

Chamadas de função e loops como for e while são avaliados somando o número de instruções básicas dentro deles. Considere o código a seguir que soma os elementos de uma lista.

def sum_list(lst):
  total = 0          # 1 instruction
  for value in lst:    
    total += value   # executed len(lst) times
  return total       # 1 instruction

Adicionamos comentários a cada linha para ajudar você a visualizar o número de instruções básicas. Se N for o comprimento de lst, então o número total de instruções básicas é 1 + N + 1 = N + 2.

Notação Big-O

Imagine que temos dois algoritmos de classificação. Calculamos o número de instruções básicas para cada uma delas e obtivemos as seguintes expressões:

À primeira vista, não é óbvio qual deles se adapta melhor. A notação Big-O oferece uma maneira de simplificar ainda mais essas expressões, aplicando essas simplificações:

1. Elimine os termos com expoentes menores
2. Remova as constantes multiplicativas

Se aplicarmos esse processo às duas expressões, obteremos N2 em ambos os casos:

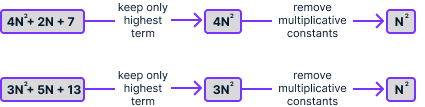
A expressão que obtemos após a simplificação é a complexidade de tempo do algoritmo, que denotamos usando O(). Nesse caso, podemos escrever que 4N2 + 2N + 7 = O(N2) e 3N2 + 5N + 13 = O(N2). Isso significa que os dois algoritmos têm a mesma complexidade de tempo, que é proporcional ao quadrado do número de elementos da lista.

Acima, calculamos que o algoritmo sum_list realizou N + 2 operações, em que N é o comprimento da lista. Aplicando as mesmas simplificações, obtemos N, portanto a complexidade de tempo de sum_list é O(N).

Isso significa que o tempo de execução é proporcional ao tamanho da lista. Isso é esperado porque, ao calcular a soma, dobrar o número de elementos em uma lista deve exigir o dobro da quantidade de trabalho, não menos, nem mais.

Notação Big-O: explicação intuitiva

Podemos ignorar os termos mais baixos porque, à medida que N aumenta, seu impacto na soma total se torna insignificante quando comparado ao termo mais alto. O gráfico a seguir mostra a contribuição de cada um dos três termos 4N2, 2N e 7 para a soma total.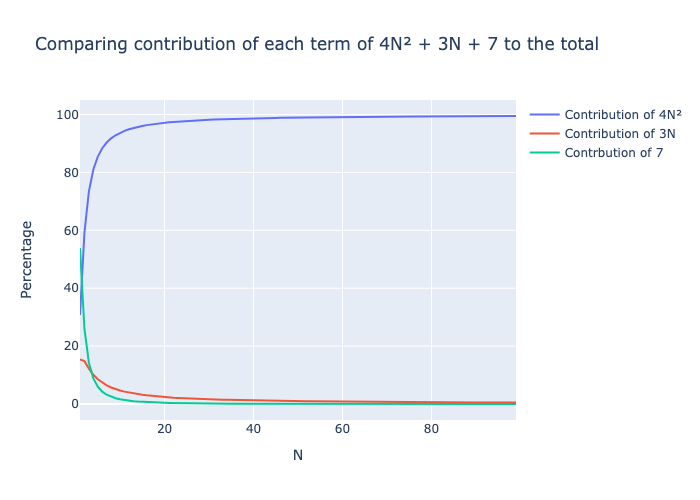

O termo quadrático 4N2 é rapidamente responsável por quase 100% do número total de operações, mesmo para valores pequenos de N. Portanto, ao lidar com grandes quantidades de dados, o tempo correspondente aos termos de ordem inferior será insignificante em comparação com os termos de ordem superior.

Deixamos de lado a constante multiplicativa porque esse valor é independente da quantidade de dados.

Notação Big-O: definição matemática

As etapas acima são suficientes, para a maioria dos fins práticos, para derivar com precisão a complexidade de tempo de um algoritmo. Podemos contar o número de instruções básicas que um algoritmo executa e obter uma expressão f(N). Depois de aplicar as duas etapas de simplificação, obtemos uma expressão simplificada g(N). Então, podemos escrever que f(N) = O(g(N)). Nós lemos isso como "f é o grande O de g".

No entanto, essa não é uma definição matemática formal e, em alguns casos, não é suficiente. 

A definição matemática é que uma função positiva f(N) = O(g(N)) se pudermos encontrar uma constante C de modo que, para valores grandes de N, o seguinte seja válido:

f(N) ≤ C × g(N)

Podemos usar a definição para mostrar que f(N) = 4N2 + 2N + 7 = O(N2). Nesse caso, podemos escolher C = 5 e ver que, para qualquer N > 4, f(N) ≤ 5 × N2:

Na prática, usaremos apenas as regras de simplificação acima.

Tipos de complexidade de tempo

Agora que entendemos os conceitos básicos da notação Big-O, vamos explorar as complexidades comuns de tempo e suas implicações, começando com a mais eficiente: tempo constante.

Tempo constante: O(1)

Como o nome sugere, os algoritmos de tempo constante têm uma complexidade de tempo constante, o que significa que seu desempenho não depende da quantidade de dados. Em geral, esses algoritmos envolvem cálculos com um número fixo de entradas, como o cálculo da distância entre dois pontos.

A distância entre dois pontos é calculada calculando a raiz quadrada da diferença entre os valores de x e y dos dois pontos.

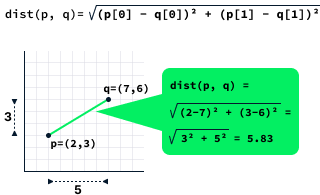
A função dist mostrada abaixo calcula a distância entre dois pontos. Ele consiste em três instruções básicas, que são uma constante. Nesse caso, escrevemos que a complexidade de tempo é O(1).

def dist(p, q):
  dx = (p[0] - q[0]) ** 2  # 1 instruction
  dy = (p[1] - q[1]) ** 2  # 1 instruction
  return (dx + dy) ** 0.5  # 1 instruction

É interessante notar que é totalmente possível que uma função apresente complexidade de tempo constante, mesmo ao processar grandes conjuntos de dados. Veja, por exemplo, o caso do cálculo do comprimento de uma lista usando a função len. Essa operação é O(1) porque a implementação mantém internamente o controle do tamanho da lista, eliminando a necessidade de contar os elementos cada vez que o comprimento é solicitado.

Tempo linear: O(N)

Discutimos anteriormente o site sum_list como um exemplo de função de tempo linear. Em geral, os algoritmos de tempo linear executam tarefas que precisam inspecionar cada ponto de dados individualmente. O cálculo do mínimo, do máximo ou da média é uma operação típica dessa categoria.

Vamos praticar analisando a seguinte função para calcular o valor mínimo de uma lista:

def minimum(lst):
  min_value = lst[0]                    # 1 instruction
  for i in range(1, len(lst)):
    min_value = min(min_value, lst[i])  # executed len(lst) - 1 times
  return min_value                      # 1 instruction

Se a lista tiver N elementos, a complexidade será 1 + (N - 1) + 1 = N + 1 = O(N).

O tempo de execução dos algoritmos de tempo linear é diretamente proporcional à quantidade de dados. Assim, se a quantidade de dados dobrar, o tempo que o algoritmo leva para processar os dados também deverá dobrar.

Tempo logarítmico: O(log(N))

O jogo de adivinhação de números envolve a tentativa de adivinhar um número oculto entre 1 e N, com o objetivo de identificar esse número com o menor número possível de adivinhações. Após cada palpite, recebemos um feedback indicando se o número oculto é maior, menor ou igual ao palpite. Se o palpite estiver correto, ganhamos o jogo; caso contrário, continuamos a adivinhar.

Uma estratégia eficaz para esse jogo é adivinhar consistentemente o ponto médio. Suponha que N = 15. Nesse caso, nosso primeiro palpite seria 8. Se o número secreto for menor que 8, sabemos que ele deve estar entre 1 e 7. Se for maior, então está entre 9 e 15. Continuamos a adivinhar o ponto médio do intervalo restante até encontrarmos a resposta correta. O diagrama abaixo ilustra os possíveis caminhos que essa estratégia pode seguir.

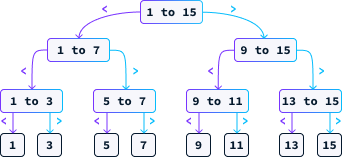
Vamos examinar a complexidade de tempo dessa abordagem. Diferentemente dos exemplos anteriores, o número de etapas desse algoritmo não depende apenas do tamanho N da entrada, pois existe a possibilidade de você adivinhar corretamente na primeira tentativa.

Ao analisar esses algoritmos, nos concentramos no pior cenário possível. Por exemplo, com N = 15, no pior caso, precisaríamos fazer 4 suposições. Cada palpite, sendo o ponto médio, elimina metade das possibilidades restantes. Na pior das hipóteses, continuamos adivinhando até que reste apenas uma possibilidade. Portanto, a questão que precisamos abordar é:

Quantas vezes devemos dividir N por 2 para obter 1?

A resposta é o logaritmo de base 2 de N, denotado como log2(N). O algoritmo implementado para identificar o número correto é conhecido como binary search. Como o número máximo de suposições é log2(N), podemos expressar sua complexidade como O(log2(N)) ou simplesmente O(log(N)), pois as constantes são insignificantes na notação de complexidade de tempo.

Devido à sua taxa de crescimento extremamente lenta, a complexidade de tempo logarítmica é muito procurada na prática, comportando-se quase como uma complexidade de tempo constante. Mesmo para valores grandes de N, o número total de operações permanece notavelmente baixo. Por exemplo, mesmo que N seja um bilhão, o número de operações necessárias é de apenas 30.

A pesquisa binária é um algoritmo fundamental na ciência da computação com inúmeras aplicações. Por exemplo, no processamento de linguagem naturalos verificadores ortográficos e os sistemas de autocorreção podem utilizar variantes de pesquisa binária para identificar com eficiência possíveis palavras candidatas.

Tempo quadrático: O(N2)

A classificação de dados é uma tarefa fundamental que os computadores precisam realizar com frequência. Um método para classificar uma lista de N números envolve a identificação iterativa do elemento mínimo da lista.

def selection_sort(lst):
  sorted_lst = []              # 1 instruction
  for _ in range(len(lst)):
    minimum = min(lst)         # executed len(lst) times
    lst.remove(minimum)        # executed len(lst) times
    sorted_lst.append(minimum) # executed len(lst) times
  return sorted_lst            # 1 instruction

Para analisar a complexidade de um loop for, avaliamos a complexidade das instruções dentro dele e, em seguida, multiplicamos esse resultado pelo número de iterações em que o loop é executado.

Computar o mínimo de uma lista e remover um elemento de uma lista são operações O(N). A adição é feita em tempo constante, O(1). Portanto, cada iteração do loop for tem uma complexidade de O(N + N + 1) = O(2N + 1), o que simplifica para O(N). Como há N iterações, a complexidade é N × O(N) = O(N2). O restante da função selection_sort() consiste em três instruções simples, de modo que a complexidade geral é O(N2 + 3) = O(N2).

Nossa análise do loop for envolveu uma simplificação excessiva. Em cada iteração, removemos um elemento da lista, o que significa que nem todas as iterações executam o mesmo número de instruções. A primeira iteração executa N instruções, a segunda executa N - 1, a terceira N - 2, e esse padrão continua até a última iteração, que executa apenas 1 instrução.

Isso implica que a verdadeira complexidade do loop for é:

N + (N - 1) + (N - 2) + … + 1 

Essa soma pode ser mostrada como sendo igual a (N2 + N) / 2. No entanto,

(N2 + N) / 2 = ½N2 + ½N = O(N2)

Mesmo que tenhamos contado a mais, a complexidade geral ainda é quadrática. A função selection_sort() exemplifica um algoritmo de classificação mais lento devido à sua complexidade quadrática, O(N2).

As funções com complexidade quadrática são mal dimensionadas, o que as torna adequadas para listas pequenas, mas impraticáveis para classificar milhões de pontos de dados, pois podem levar dias para concluir a tarefa. A duplicação da quantidade de dados leva a uma quadruplicação do tempo de execução.

Tempo loglinear: O(N log(N))

É possível criar um algoritmo para classificar uma lista com complexidade de tempo O(N log(N)). Um desses algoritmos é chamado merge sort.  Não entraremos em detalhes sobre sua implementação, mas se você quiser saber mais sobre isso, confira esta introdução rápida à classificação de mesclagem deste curso sobre Estruturas de dados e algoritmos em Python.

Conforme mencionado anteriormente, a complexidade logarítmica se comporta de forma semelhante à complexidade constante na prática. Portanto, o tempo de execução de um algoritmo O(N log(N)) pode ser comparável ao de um algoritmo de tempo linear em aplicativos do mundo real.

O gráfico a seguir mostra que N log(N) e N crescem a taxas semelhantes, enquanto N2 cresce muito rápido, tornando-se rapidamente muito lento.

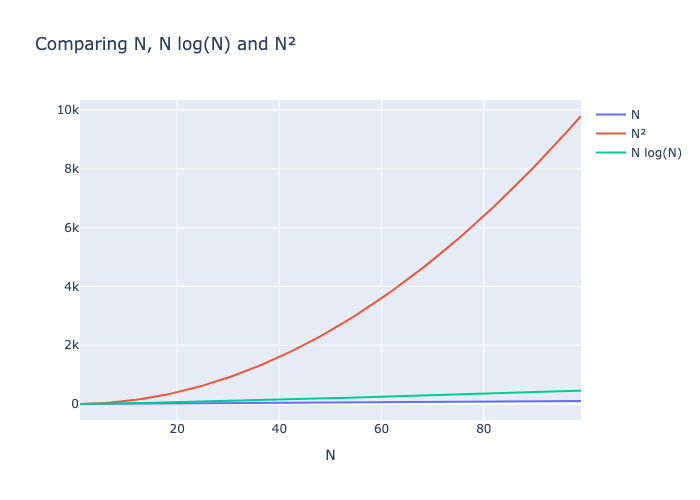
Tempo cúbico: O(N3)

Um algoritmo de complexidade de tempo cúbico amplamente usado em IA é a multiplicação de matrizes, que desempenha um papel fundamental na funcionalidade de modelos de linguagem grandes, como o GPT. Esse algoritmo é fundamental para os cálculos realizados durante as fases de treinamento e inferência.

Para multiplicar duas matrizes N por N, A e B, precisamos multiplicar cada linha da primeira matriz A por cada coluna da segunda matriz B. Especificamente, o valor do produto na entrada (i, j) é determinado pela multiplicação dos elementos na linha i de A pelos elementos correspondentes na coluna j de B.

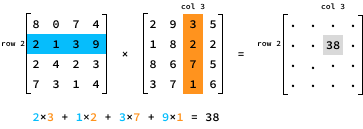
Aqui está uma implementação Python da multiplicação de matrizes:

def matrix_mul(A, B):
  n = len(A)                                       # 1 instruction
  res = [[0 for _ in range(n)] for _ in range(n)]  # N^2 instructions
  for i in range(n):
    for j in range(n):
      for k in range(n):
        res[i][j] += A[i][k] * B[k][j]             # executed N×N×N = N^3 times
  return res                                       # 1 instruction

No total, o site matrix_mul() executa N3 + N2 + 2 instruções, portanto, sua complexidade de tempo é O(N3).

Como alternativa, poderíamos ter analisado a complexidade raciocinando sobre os cálculos. O resultado da multiplicação da matriz tem N2 entradas. Cada entrada leva O(N) tempo para ser computada, de modo que a complexidade geral é N2 × O(N) = O(N3).

Os algoritmos de tempo cúbico são bastante lentos. Dobrar a quantidade de dados resulta em um fator de oito no tempo de execução, o que faz com que esses algoritmos sejam muito mal dimensionados. Mesmo para um valor relativamente pequeno de N, o número de instruções aumenta muito rapidamente.

A multiplicação de matrizes é um exemplo de um desafio computacional em que os avanços no hardware tiveram um impacto significativo. Embora existam algoritmos um pouco mais eficientes para a multiplicação de matrizes, foram principalmente os avanços no design dos chips de GPU - adaptados especificamente para a multiplicação de matrizes - que facilitaram significativamente o treinamento de modelos grandes como o GPT em prazos razoáveis.

Mais recentemente, os pesquisadores propuseram a eliminação da multiplicação de matrizes de grandes modelos de aprendizagem - você pode ler mais sobre isso neste artigo em LLMs sem MatMul: Principais conceitos explicados.

Complexidade de tempo exponencial: O(2N) e O(N!)

Normalmente, os algoritmos de tempo exponencial surgem quando um problema é resolvido explorando-se todas as soluções possíveis. Considere o planejamento de uma rota para um caminhão de entrega que precisa visitar N locais de entrega. Uma abordagem para resolver esse problema é avaliar todas as ordens de entrega possíveis. A ferramenta Python itertools do Python oferece um método simples para você percorrer todas as permutações de uma lista.

import itertools
for order in itertools.permutations([1, 2, 3]):
  print(order)

(1, 2, 3)
(1, 3, 2)
(2, 1, 3)
(2, 3, 1)
(3, 1, 2)
(3, 2, 1)

O número de permutações de uma lista de comprimento N é denotado por N!, lido como "N fatorial". A função fatorial apresenta crescimento exponencial. Por exemplo, quando N = 13, o número de permutações ultrapassa 1 bilhão.

Suponha que os locais de entrega sejam fornecidos como uma lista de pontos 2D. Nesse caso, podemos determinar a sequência de entrega que minimiza a distância total, iterando por todas as sequências possíveis e mantendo o controle da melhor.

def optimize_route(locations):
  minimum_distance = float("inf")                  # 1 instruction
  best_order = None                                # 1 instruction
  for order in itertools.permutations(locations):  # N! iterations
    distance = 0                                   # 1 instruction, N! times
    for i in range(1, len(order)):                 
      distance += dist(order[i - 1], order[i])     # N-1 instructions, N! times
    if distance < minimum_distance:                
      distance = minimum_distance                  # 1 instruction, N! times
      best_order = order                           # 1 instruction, N! times
  return best_order                                # 1 instruction

O primeiro loop for é executado N! vezes. Portanto, o número de operações em optimize_route() é N! x (1 + N - 1 + 2) + 3 = N! x (N + 2) + 3 = N! x N + 2N! + 3.

Aprendemos que, ao calcular a complexidade de tempo, ignoramos os termos de expoente inferior. No entanto, nesse cenário, encontramos um termo N!, que não é uma potência de N. Podemos refinar nossa estratégia de simplificação optando por omitir os termos com taxas de crescimento mais lentas. A tabela abaixo lista os termos comumente encontrados na complexidade de tempo de um algoritmo, organizados da menor para a maior taxa de crescimento.

Assim, podemos expressar a complexidade de tempo do optimize_route() como N! x N + 2N! + 3 = O(N! x N).

Em geral, os algoritmos de complexidade de tempo exponencial são eficientes apenas para resolver instâncias muito pequenas. Mesmo com apenas 13 locais, o número de permutações ultrapassa 1 bilhão, o que torna esse algoritmo impraticável para cenários do mundo real.

Complexidade de tempo: Pior caso e melhor caso

Com o jogo de adivinhação de números, nos concentramos na complexidade do pior caso. Ao nos concentrarmos no pior caso, garantimos a taxa de crescimento do tempo de execução do algoritmo.

No melhor caso, adivinhamos na primeira vez, portanto, uma análise de complexidade no melhor caso resultaria em complexidade O(1). Isso é preciso - na melhor das hipóteses, precisamos de uma única operação constante. No entanto, isso não é muito útil porque é muito improvável.

Em geral, quando analisamos a complexidade de um algoritmo, sempre nos concentramos no pior caso, porque:

1. Garantia de desempenho: Ao nos concentrarmos na complexidade do pior caso, podemos garantir que nosso algoritmo nunca terá um desempenho pior do que um determinado limite. Isso é fundamental para aplicativos que exigem desempenho confiável, como sistemas em tempo real, em que os atrasos podem causar problemas significativos.
2. Segurança e confiabilidade: A análise do pior caso ajuda a projetar algoritmos robustos que podem lidar com os cenários mais exigentes. Isso garante que o algoritmo ainda funcionará dentro dos limites aceitáveis, mesmo nas piores situações possíveis.
3. Limite superior: Conhecer a complexidade do pior caso nos dá um limite superior para o desempenho. Isso é útil para você entender os recursos máximos (tempo, memória) que um algoritmo pode exigir.

Complexidade de tempo: Implicações práticas

A complexidade do tempo pode parecer um assunto muito teórico, mas pode ser muito útil na prática.

Por exemplo, se uma função lida consistentemente com um conjunto de dados pequeno, um O(N2) pode ser mais adequado do que um algoritmo O(N) complexo e difícil de manter. No entanto, essa deve ser uma decisão deliberada para evitar ser pego de surpresa quando o aplicativo não puder lidar com o aumento do tráfego de usuários.

A análise da complexidade do tempo revela que pequenas otimizações de código têm um efeito insignificante no tempo de execução de um algoritmo. Melhorias significativas são obtidas com a redução fundamental do número de operações básicas necessárias para computar o resultado. Em geral, é preferível manter um código limpo e compreensível a otimizá-lo a ponto de torná-lo ininteligível.

As partes mais lentas do código dominarão as outras. Normalmente, não faz sentido otimizar a parte mais rápida antes de otimizar a mais lenta. Por exemplo, imagine que temos uma função que executa duas tarefas:

def process_data(data):
  clean_data(data)
  analyze_data(data)

Se a função clean_data() tiver complexidade O(N2) e analyze_data() tem complexidade O(N3), então a redução da complexidade de clean_data() não melhorará a complexidade geral de process_data(). É melhor você se concentrar em melhorar a função analyze_data().

Além disso, a complexidade do tempo pode informar as decisões de hardware. Por exemplo, um O(N3), apesar de sua baixa escalabilidade, ainda pode ser rápido o suficiente para tarefas com dados limitados se for executado em um hardware superior ou em uma linguagem de programação mais rápida. Por outro lado, se um algoritmo tiver uma complexidade de tempo exponencial O(2N), nenhuma atualização de hardware será suficiente, indicando a necessidade de um algoritmo mais eficiente.

Conclusão

Apesar de os computadores estarem cada vez mais rápidos, estamos lidando com mais dados do que nunca. Pense assim: toda vez que usamos a Internet, smartphones ou dispositivos domésticos inteligentes, criamos toneladas de informações. À medida que essa montanha de dados cresce, fica mais difícil classificá-los e encontrar o que é importante. Por isso, é muito importante que você continue aprimorando nossas ferramentas, especialmente os algoritmos, para lidar e entender todas essas informações.

A análise da complexidade do tempo oferece uma estrutura direta para o raciocínio sobre o tempo de execução de um algoritmo. Seu principal objetivo é fornecer informações sobre a taxa de crescimento da complexidade de tempo, em vez de prever tempos de execução exatos. Apesar das inúmeras simplificações e suposições do modelo, ele provou ser extremamente útil na prática, capturando com eficácia a essência dos comportamentos do tempo de execução do algoritmo.

Se você quiser explorar mais assuntos de ciência da computação, confira meu artigo sobre Data Structures: Um guia abrangente com exemplos em Python.