Redes neuronales convolucionales en Python con Keras

Puede que ya hayas oído hablar del reconocimiento facial o de imágenes, o de los coches autónomos. Se trata de implementaciones reales de Redes Neuronales Convolucionales (CNN). En esta entrada del blog, aprenderás y comprenderás cómo implementar estas redes neuronales artificiales profundas y de alimentación hacia delante en Keras y también aprenderás a superar el sobreajuste con la técnica de regularización llamada "abandono".

Más concretamente, en el tutorial de hoy abordarás los siguientes temas:

• Se te presentarán las redes neuronales convolucionales;
• Entonces, primero intentarás comprender los datos. Utilizarás Python y sus bibliotecas para cargar, explorar y analizar tus datos,
• Después, preprocesarás tus datos: aprenderás a redimensionar, reescalar, convertir tus etiquetas en vectores de codificación de un solo golpe y dividir tus datos en conjuntos de entrenamiento y validación;
• Con todo esto hecho, puedes construir el modelo de red neuronal: aprenderás a modelar los datos y a formar la red. A continuación, compilarás, entrenarás y evaluarás el modelo, visualizando los gráficos de precisión y pérdida;
• A continuación, conocerás el concepto de sobreajuste y cómo puedes superarlo añadiendo una capa de abandono;
• Con esta información, puedes revisar tu modelo original y volver a entrenarlo. También volverás a evaluar tu nuevo modelo y compararás los resultados de ambos;
• A continuación, harás predicciones sobre los datos de prueba, convertirás las probabilidades en etiquetas de clase y trazarás unas cuantas muestras de prueba que tu modelo haya clasificado correctamente y otras que haya clasificado incorrectamente;
• Por último, visualizarás el informe de clasificación, que te dará una intuición más profunda sobre qué clase fue (in)correctamente clasificada por tu modelo.

¿Quieres hacer un curso sobre Keras y aprendizaje profundo en Python? ¡Considera la posibilidad de realizar el curso de Aprendizaje Profundo en Python de DataCamp!

Además, ¡no te pierdas nuestra hoja de trucos de Keras, que te muestra los seis pasos que debes seguir para construir redes neuronales en Python con ejemplos de código!

Red neuronal convolucional: Introducción

A estas alturas, puede que ya conozcas el aprendizaje automático y el aprendizaje profundo, una rama de la informática que estudia el diseño de algoritmos capaces de aprender. El aprendizaje profundo es un subcampo del aprendizaje automático que se inspira en las redes neuronales artificiales, que a su vez se inspiran en las redes neuronales biológicas.

Un tipo específico de red neuronal profunda de este tipo es la red convolucional, que suele denominarse CNN o ConvNet. Es una red neuronal artificial profunda y de avance. Recuerda que las redes neuronales feed-forward también se denominan perceptrones multicapa (MLP), que son los modelos de aprendizaje profundo por excelencia. Los modelos se llaman "feed-forward" porque la información fluye a través del modelo. No hay conexiones de retroalimentación en las que las salidas del modelo se retroalimenten a sí mismas.

Las CNN se inspiran específicamente en la corteza visual biológica. El córtex tiene pequeñas regiones de células sensibles a zonas concretas del campo visual. Esta idea fue ampliada por un cautivador experimento realizado por Hubel y Wiesel en 1962 (si quieres saber más, aquí tienes un vídeo). En este experimento, los investigadores demostraron que algunas neuronas individuales del cerebro se activaban o disparaban sólo en presencia de bordes de una orientación determinada, como bordes verticales u horizontales. Por ejemplo, algunas neuronas se disparaban cuando se exponían a lados verticales y otras cuando se les mostraba un borde horizontal. Hubel y Wiesel descubrieron que todas estas neuronas estaban bien ordenadas de forma columnar y que juntas eran capaces de producir la percepción visual. Esta idea de componentes especializados dentro de un sistema que tienen tareas específicas es algo que también utilizan las máquinas y que también puedes encontrar en las CNN.

Las redes neuronales convolucionales han sido una de las innovaciones más influyentes en el campo de la visión por ordenador. Han funcionado mucho mejor que la visión por ordenador tradicional y han producido resultados de vanguardia. Estas redes neuronales han demostrado su eficacia en muchos estudios de casos y aplicaciones de la vida real, como:

• Clasificación de imágenes, detección de objetos, segmentación, reconocimiento facial;
• Coches autoconducidos que aprovechan los sistemas de visión basados en CNN;
• Clasificación de la estructura cristalina mediante una red neuronal convolucional;
• Y muchos más, ¡por supuesto!

Para entender este éxito, tendrás que remontarte a 2012, año en el que Alex Krizhevsky utilizó redes neuronales convolucionales para ganar el Concurso ImageNet de ese año, reduciendo el error de clasificación del 26% al 15%.

Ten en cuenta que ImageNet Large Scale Visual Recognition Challenge (ILSVRC) comenzó en el año 2010 y es una competición anual en la que los equipos de investigación evalúan sus algoritmos en el conjunto de datos dado y compiten para conseguir una mayor precisión en varias tareas de reconocimiento visual.

Fue entonces cuando las redes neuronales recuperaron protagonismo después de bastante tiempo. A menudo se denomina a esto la "tercera ola de redes neuronales". Las otras dos oleadas se produjeron en los años 40 hasta los 60 y en los 70 hasta los 80.

De acuerdo, sabes que trabajarás con redes feed-forward inspiradas en el córtex visual biológico, pero ¿qué significa eso en realidad?

Echa un vistazo a la siguiente imagen:

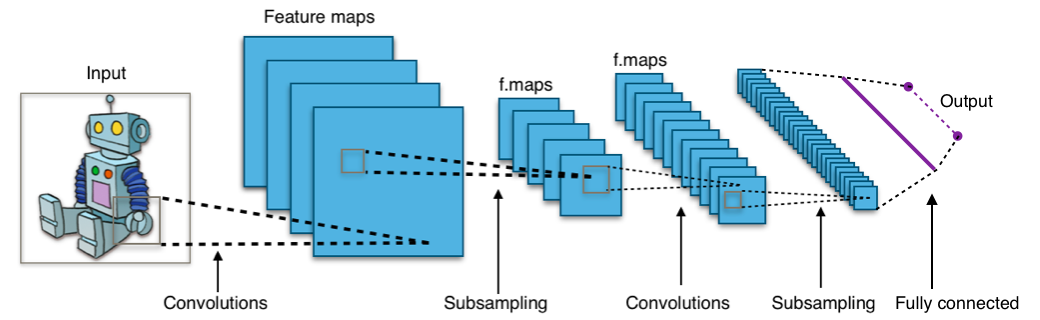
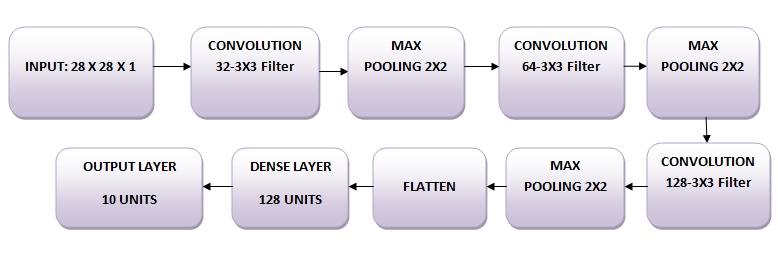
La imagen te muestra que alimentas una imagen como entrada a la red, que pasa por múltiples convoluciones, submuestreo, una capa totalmente conectada y finalmente emite algo.

Pero, ¿qué son todos estos conceptos?

1. La capa de convolución calcula la salida de las neuronas que están conectadas a regiones locales o campos receptivos en la entrada, calculando cada una un producto punto entre sus pesos y un pequeño campo receptivo al que están conectadas en el volumen de entrada. Cada cálculo conduce a la extracción de un mapa de características de la imagen de entrada. En otras palabras, imagina que tienes una imagen representada como una matriz de valores de 5x5, y tomas una matriz de 3x3 y deslizas esa ventana o núcleo de 3x3 alrededor de la imagen. En cada posición de esa matriz, multiplicas los valores de tu ventana de 3x3 por los valores de la imagen que actualmente cubre la ventana. Como resultado, obtendrás un único número que representa todos los valores de esa ventana de las imágenes. Utilizas esta capa para filtrar: a medida que la ventana se desplaza sobre la imagen, compruebas si hay patrones en esa sección de la imagen. Esto funciona gracias a los filtros, que se multiplican por los valores resultantes de la convolución.
2. El objetivo del submuestreo es obtener una representación de entrada reduciendo sus dimensiones, lo que ayuda a reducir el sobreajuste. Una de las técnicas de submuestreo es la agrupación de máximos. Con esta técnica, seleccionas el valor de píxel más alto de una región en función de su tamaño. En otras palabras, la agrupación máxima toma el valor más grande de la ventana de la imagen actualmente cubierta por el núcleo. Por ejemplo, puedes tener una capa de agrupación máxima de tamaño 2 x 2 seleccionará el valor máximo de intensidad de píxel de la región de 2 x 2. Tienes razón al pensar que la capa de agrupación funciona entonces de forma muy parecida a la capa de convolución. También se toma un núcleo o una ventana y se desplaza sobre la imagen; la única diferencia es que la función que se aplica al núcleo y a la ventana de la imagen no es lineal.
   
   
   
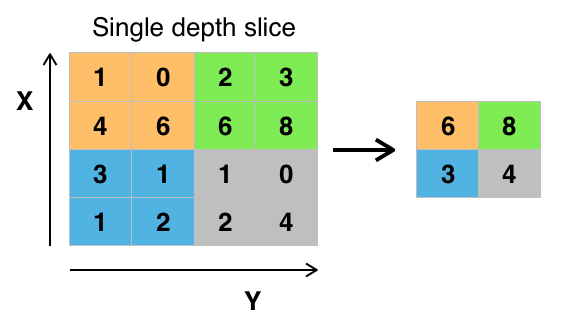   Figura: Max-Pooling de Wikipedia
3. El objetivo de la capa totalmente conectada es aplanar las características de alto nivel aprendidas por las capas convolucionales y combinar todas las características. Pasa la salida aplanada a la capa de salida, donde utiliza un clasificador softmax o un sigmoide para predecir la etiqueta de clase de entrada.

Para más información, puedes ir aquí.

El conjunto de datos Moda-MNIST

Antes de seguir adelante y cargar los datos, ¡es bueno echar un vistazo a con qué vas a trabajar exactamente! El conjunto de datos Moda-MNIST es un conjunto de datos de imágenes de artículos de Zalando, con imágenes en escala de grises de 28x28 de 70.000 productos de moda de 10 categorías, y 7.000 imágenes por categoría. El conjunto de entrenamiento tiene 60.000 imágenes, y el conjunto de prueba tiene 10.000 imágenes. Puedes volver a comprobarlo más tarde, cuando hayas cargado los datos ;)

Fashion-MNIST es similar al conjunto de datos MNIST que quizá ya conozcas, que se utiliza para clasificar dígitos escritos a mano. Esto significa que las dimensiones de las imágenes y las divisiones de entrenamiento y prueba son similares a las del conjunto de datos MNIST. Consejo: si quieres aprender a implementar un Perceptrón Multicapa (MLP) para tareas de clasificación con este último conjunto de datos, ve a este tutorial de aprendizaje profundo con Keras.

Puedes encontrar el conjunto de datos Fashion-MNIST aquí, pero también puedes cargarlo con la ayuda de módulos específicos de TensorFlow y Keras. Verás cómo funciona en la siguiente sección.

Carga los datos

Keras viene con una biblioteca llamada datasets, que puedes utilizar para cargar conjuntos de datos nada más sacarlos de la caja: descargas los datos del servidor y aceleras el proceso, puesto que ya no tienes que descargar los datos a tu ordenador. Las imágenes de entrenamiento y de prueba, junto con las etiquetas, se cargan y almacenan en las variables train_X, train_Y, test_X, test_Y, respectivamente.

from keras.datasets import fashion_mnist
(train_X,train_Y), (test_X,test_Y) = fashion_mnist.load_data()

Using TensorFlow backend.

¡Estupendo! Ha sido bastante sencillo, ¿verdad?

Probablemente ya hayas hecho esto un millón de veces, pero siempre es un paso esencial para empezar. ¡Ahora estás completamente preparado para empezar a analizar, procesar y modelar tus datos!

Analiza los datos

Analicemos ahora cómo son las imágenes del conjunto de datos. Aunque a estas alturas ya conozcas la dimensión de las imágenes, sigue mereciendo la pena el esfuerzo de analizarlo programáticamente: puede que tengas que reescalar los píxeles de la imagen y cambiar el tamaño de las imágenes.

import numpy as np
from keras.utils import to_categorical
import matplotlib.pyplot as plt
%matplotlib inline

print('Training data shape : ', train_X.shape, train_Y.shape)

print('Testing data shape : ', test_X.shape, test_Y.shape)

('Training data shape : ', (60000, 28, 28), (60000,))
('Testing data shape : ', (10000, 28, 28), (10000,))

En el resultado anterior, puedes ver que los datos de entrenamiento tienen una forma de 60000 x 28 x 28, ya que hay 60.000 muestras de entrenamiento, cada una de 28 x 28 dimensiones. Del mismo modo, los datos de prueba tienen una forma de 10000 x 28 x 28, ya que hay 10.000 muestras de prueba.

# Find the unique numbers from the train labels
classes = np.unique(train_Y)
nClasses = len(classes)
print('Total number of outputs : ', nClasses)
print('Output classes : ', classes)

('Total number of outputs : ', 10)
('Output classes : ', array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9], dtype=uint8))

También hay un total de diez clases de salida que van de 0 a 9.

Además, no olvides echar un vistazo a las imágenes de tu conjunto de datos:

plt.figure(figsize=[5,5])

# Display the first image in training data
plt.subplot(121)
plt.imshow(train_X[0,:,:], cmap='gray')
plt.title("Ground Truth : {}".format(train_Y[0]))

# Display the first image in testing data
plt.subplot(122)
plt.imshow(test_X[0,:,:], cmap='gray')
plt.title("Ground Truth : {}".format(test_Y[0]))

Text(0.5,1,u'Ground Truth : 9')

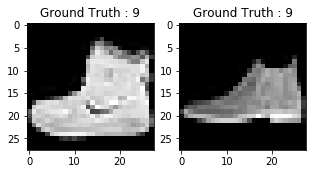
La salida de los dos gráficos anteriores parece un botín, y a esta clase se le asigna una etiqueta de clase 9. Del mismo modo, otros productos de moda tendrán etiquetas diferentes, pero los productos similares tendrán las mismas etiquetas. Esto significa que todas las 7.000 imágenes de botines tendrán una etiqueta de clase 9.

Preprocesamiento de datos

Como puedes ver en el gráfico anterior, las imágenes están en escala de grises y tienen valores de píxel que van de 0 a 255. Además, estas imágenes tienen una dimensión de 28 x 28. En consecuencia, tendrás que preprocesar los datos antes de introducirlos en el modelo.

• Como primer paso, convierte cada imagen de 28 x 28 del conjunto de entrenamiento y prueba en una matriz de tamaño 28 x 28 x 1 que se introduce en la red.

train_X = train_X.reshape(-1, 28,28, 1)
test_X = test_X.reshape(-1, 28,28, 1)
train_X.shape, test_X.shape

((60000, 28, 28, 1), (10000, 28, 28, 1))

• Los datos ahora mismo están en formato int8, así que antes de introducirlos en la red tienes que convertir su tipo a float32, y también tienes que reescalar los valores de los píxeles en el rango 0 - 1 inclusive. Así que ¡hagámoslo!

train_X = train_X.astype('float32')
test_X = test_X.astype('float32')
train_X = train_X / 255.
test_X = test_X / 255.

• Ahora tienes que convertir las etiquetas de clase en un vector de codificación de un solo golpe.

En la codificación de un solo golpe, conviertes los datos categóricos en un vector de números. La razón por la que conviertes los datos categóricos en una codificación caliente es que los algoritmos de aprendizaje automático no pueden trabajar con datos categóricos directamente. Genera una columna booleana para cada categoría o clase. Sólo una de estas columnas podía tomar el valor 1 para cada muestra. De ahí el término codificación de una sola vez.

Para el enunciado de tu problema, la codificación en caliente será un vector de filas, y para cada imagen, tendrá una dimensión de 1 x 10. Lo importante aquí es que el vector está formado por todos ceros, excepto la clase que representa, para la que es 1. Por ejemplo, la imagen de los botines que has representado anteriormente tiene una etiqueta de 9, por lo que para todas las imágenes de los botines, el único vector de codificación caliente sería [0 0 0 0 0 0 0 0 1 0].

Así que convirtamos las etiquetas de entrenamiento y de prueba en vectores de codificación de un solo golpe:

# Change the labels from categorical to one-hot encoding
train_Y_one_hot = to_categorical(train_Y)
test_Y_one_hot = to_categorical(test_Y)

# Display the change for category label using one-hot encoding
print('Original label:', train_Y[0])
print('After conversion to one-hot:', train_Y_one_hot[0])

('Original label:', 9)
('After conversion to one-hot:', array([ 0.,  0.,  0.,  0.,  0.,  0.,  0.,  0.,  0.,  1.]))

Está bastante claro, ¿no? Ten en cuenta que también puedes imprimir la página train_Y_one_hot, que mostrará una matriz de tamaño 60000 x 10 en la que cada fila representa la codificación de un disparo de una imagen.

• Este último paso es crucial. En el aprendizaje automático o en cualquier tarea específica de datos, debes particionar los datos correctamente. Para que el modelo generalice bien, divide los datos de entrenamiento en dos partes, una destinada al entrenamiento y otra a la validación. En este caso, entrenarás el modelo con el 80\% de los datos de entrenamiento y lo validarás con el 20\% de los datos de entrenamiento restantes. Esto también ayudará a reducir el sobreajuste, ya que estarás validando el modelo en los datos que no habría visto en la fase de entrenamiento, lo que ayudará a aumentar el rendimiento en la prueba.

from sklearn.model_selection import train_test_split
train_X,valid_X,train_label,valid_label = train_test_split(train_X, train_Y_one_hot, test_size=0.2, random_state=13)

Por última vez, comprobemos la forma del conjunto de entrenamiento y validación.

train_X.shape,valid_X.shape,train_label.shape,valid_label.shape

((48000, 28, 28, 1), (12000, 28, 28, 1), (48000, 10), (12000, 10))

La Red

Las imágenes son de tamaño 28 x 28. Conviertes la matriz de la imagen en una matriz, la reescalas entre 0 y 1, le das nueva forma para que tenga un tamaño de 28 x 28 x 1, y alimentas esto como entrada a la red.

Utilizarás tres capas convolucionales:

• La primera capa tendrá 32-3 x 3 filtros,
• La segunda capa tendrá 64 filtros de 3 x 3 y
• La tercera capa tendrá 128-3 x 3 filtros.

Además, hay tres capas de agrupamiento máximo, cada una de tamaño 2 x 2.

Modela los datos

En primer lugar, vamos a importar todos los módulos necesarios para entrenar el modelo.

import keras
from keras.models import Sequential,Input,Model
from keras.layers import Dense, Dropout, Flatten
from keras.layers import Conv2D, MaxPooling2D
from keras.layers.normalization import BatchNormalization
from keras.layers.advanced_activations import LeakyReLU

Utilizarás un tamaño de lote de 64. También es preferible un tamaño de lote mayor, de 128 o 256. Todo depende de la memoria. Contribuye masivamente a determinar los parámetros de aprendizaje y afecta a la precisión de la predicción. Entrenarás la red durante 20 épocas.

batch_size = 64
epochs = 20
num_classes = 10

Arquitectura de la red neuronal

En Keras, puedes simplemente apilar capas añadiendo la capa deseada una a una. Eso es exactamente lo que harás aquí: primero añadirás una primera capa convolucional con Conv2D(). ¡Ten en cuenta que utilizas esta función porque estás trabajando con imágenes! A continuación, añade la función de activación ReLU Leaky, que ayuda a la red a aprender límites de decisión no lineales. Como tienes diez clases diferentes, necesitarás una frontera de decisión no lineal que pueda separar estas diez clases que no son linealmente separables.

Más concretamente, añades ReLUs con fugas porque intentan solucionar el problema de las Unidades Lineales Rectificadas (ReLUs) moribundas. La función de activación ReLU se utiliza mucho en las arquitecturas de redes neuronales y, más concretamente, en las redes convolucionales, donde ha demostrado ser más eficaz que la función sigmoidea logística, ampliamente utilizada. En 2017, esta función de activación es la más popular para las redes neuronales profundas. La función ReLU permite umbralizar la activación a cero. Sin embargo, durante el entrenamiento, las unidades ReLU pueden "morir". Esto puede ocurrir cuando un gradiente grande fluye a través de una neurona ReLU: puede hacer que los pesos se actualicen de tal manera que la neurona no vuelva a activarse en ningún punto de datos. Si esto ocurre, entonces el gradiente que fluye a través de la unidad será siempre cero a partir de ese punto. Las ReLUs con fugas intentan resolver esto: la función no será cero, sino que tendrá una pequeña pendiente negativa.

A continuación, añadirás la capa de agrupamiento máximo con MaxPooling2D() y así sucesivamente. La última capa es una capa Densa que tiene una función de activación softmax con 10 unidades, necesaria para este problema de clasificación multiclase.

fashion_model = Sequential()
fashion_model.add(Conv2D(32, kernel_size=(3, 3),activation='linear',input_shape=(28,28,1),padding='same'))
fashion_model.add(LeakyReLU(alpha=0.1))
fashion_model.add(MaxPooling2D((2, 2),padding='same'))
fashion_model.add(Conv2D(64, (3, 3), activation='linear',padding='same'))
fashion_model.add(LeakyReLU(alpha=0.1))
fashion_model.add(MaxPooling2D(pool_size=(2, 2),padding='same'))
fashion_model.add(Conv2D(128, (3, 3), activation='linear',padding='same'))
fashion_model.add(LeakyReLU(alpha=0.1))                  
fashion_model.add(MaxPooling2D(pool_size=(2, 2),padding='same'))
fashion_model.add(Flatten())
fashion_model.add(Dense(128, activation='linear'))
fashion_model.add(LeakyReLU(alpha=0.1))                  
fashion_model.add(Dense(num_classes, activation='softmax'))

Compilar el modelo

Una vez creado el modelo, compílalo utilizando el optimizador Adam, uno de los algoritmos de optimización más populares. Puedes leer más sobre este optimizador aquí. Además, especifica el tipo de pérdida, que es la entropía cruzada categórica, que se utiliza para la clasificación multiclase; también puedes utilizar la entropía cruzada binaria como función de pérdida. Por último, especifica las métricas como la precisión que quieres analizar mientras se entrena el modelo.

fashion_model.compile(loss=keras.losses.categorical_crossentropy, optimizer=keras.optimizers.Adam(),metrics=['accuracy'])

Vamos a visualizar las capas que has creado en el paso anterior utilizando la función resumen. Esto mostrará algunos parámetros (pesos y sesgos) en cada capa y también los parámetros totales de tu modelo.

fashion_model.summary()

_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
conv2d_51 (Conv2D)           (None, 28, 28, 32)        320       
_________________________________________________________________
leaky_re_lu_57 (LeakyReLU)   (None, 28, 28, 32)        0         
_________________________________________________________________
max_pooling2d_49 (MaxPooling (None, 14, 14, 32)        0         
_________________________________________________________________
conv2d_52 (Conv2D)           (None, 14, 14, 64)        18496     
_________________________________________________________________
leaky_re_lu_58 (LeakyReLU)   (None, 14, 14, 64)        0         
_________________________________________________________________
max_pooling2d_50 (MaxPooling (None, 7, 7, 64)          0         
_________________________________________________________________
conv2d_53 (Conv2D)           (None, 7, 7, 128)         73856     
_________________________________________________________________
leaky_re_lu_59 (LeakyReLU)   (None, 7, 7, 128)         0         
_________________________________________________________________
max_pooling2d_51 (MaxPooling (None, 4, 4, 128)         0         
_________________________________________________________________
flatten_17 (Flatten)         (None, 2048)              0         
_________________________________________________________________
dense_33 (Dense)             (None, 128)               262272    
_________________________________________________________________
leaky_re_lu_60 (LeakyReLU)   (None, 128)               0         
_________________________________________________________________
dense_34 (Dense)             (None, 10)                1290      
=================================================================
Total params: 356,234
Trainable params: 356,234
Non-trainable params: 0
_________________________________________________________________

Entrenar al modelo

¡Por fin ha llegado el momento de entrenar el modelo con la función fit() de Keras! El modelo se entrena durante 20 épocas. La función fit() devolverá un objeto history; al narrar el resultado de esta función en fashion_train, podrás utilizarlo más adelante para trazar los gráficos de precisión y de función de pérdida entre el entrenamiento y la validación, lo que te ayudará a analizar visualmente el rendimiento de tu modelo.

fashion_train = fashion_model.fit(train_X, train_label, batch_size=batch_size,epochs=epochs,verbose=1,validation_data=(valid_X, valid_label))

Train on 48000 samples, validate on 12000 samples
Epoch 1/20
48000/48000 [==============================] - 60s 1ms/step - loss: 0.4661 - acc: 0.8311 - val_loss: 0.3320 - val_acc: 0.8809
Epoch 2/20
48000/48000 [==============================] - 60s 1ms/step - loss: 0.2874 - acc: 0.8951 - val_loss: 0.2781 - val_acc: 0.8963
Epoch 3/20
48000/48000 [==============================] - 60s 1ms/step - loss: 0.2420 - acc: 0.9111 - val_loss: 0.2501 - val_acc: 0.9077
Epoch 4/20
48000/48000 [==============================] - 59s 1ms/step - loss: 0.2088 - acc: 0.9226 - val_loss: 0.2369 - val_acc: 0.9147
Epoch 5/20
48000/48000 [==============================] - 59s 1ms/step - loss: 0.1838 - acc: 0.9324 - val_loss: 0.2602 - val_acc: 0.9070
Epoch 6/20
48000/48000 [==============================] - 59s 1ms/step - loss: 0.1605 - acc: 0.9396 - val_loss: 0.2264 - val_acc: 0.9193
Epoch 7/20
48000/48000 [==============================] - 59s 1ms/step - loss: 0.1356 - acc: 0.9488 - val_loss: 0.2566 - val_acc: 0.9180
Epoch 8/20
48000/48000 [==============================] - 59s 1ms/step - loss: 0.1186 - acc: 0.9553 - val_loss: 0.2556 - val_acc: 0.9149
Epoch 9/20
48000/48000 [==============================] - 59s 1ms/step - loss: 0.0985 - acc: 0.9634 - val_loss: 0.2681 - val_acc: 0.9204
Epoch 10/20
48000/48000 [==============================] - 59s 1ms/step - loss: 0.0873 - acc: 0.9670 - val_loss: 0.2712 - val_acc: 0.9221
Epoch 11/20
48000/48000 [==============================] - 59s 1ms/step - loss: 0.0739 - acc: 0.9721 - val_loss: 0.2757 - val_acc: 0.9202
Epoch 12/20
48000/48000 [==============================] - 60s 1ms/step - loss: 0.0628 - acc: 0.9767 - val_loss: 0.3126 - val_acc: 0.9132
Epoch 13/20
48000/48000 [==============================] - 61s 1ms/step - loss: 0.0569 - acc: 0.9789 - val_loss: 0.3556 - val_acc: 0.9081
Epoch 14/20
48000/48000 [==============================] - 60s 1ms/step - loss: 0.0452 - acc: 0.9833 - val_loss: 0.3441 - val_acc: 0.9189
Epoch 15/20
48000/48000 [==============================] - 60s 1ms/step - loss: 0.0421 - acc: 0.9847 - val_loss: 0.3400 - val_acc: 0.9165
Epoch 16/20
48000/48000 [==============================] - 60s 1ms/step - loss: 0.0379 - acc: 0.9861 - val_loss: 0.3876 - val_acc: 0.9195
Epoch 17/20
48000/48000 [==============================] - 60s 1ms/step - loss: 0.0405 - acc: 0.9855 - val_loss: 0.4112 - val_acc: 0.9164
Epoch 18/20
48000/48000 [==============================] - 60s 1ms/step - loss: 0.0285 - acc: 0.9897 - val_loss: 0.4150 - val_acc: 0.9181
Epoch 19/20
48000/48000 [==============================] - 61s 1ms/step - loss: 0.0322 - acc: 0.9877 - val_loss: 0.4584 - val_acc: 0.9196
Epoch 20/20
48000/48000 [==============================] - 61s 1ms/step - loss: 0.0262 - acc: 0.9906 - val_loss: 0.4396 - val_acc: 0.9205

¡Por fin! Has entrenado el modelo en moda-MNIST durante 20 épocas, y observando la precisión y la pérdida del entrenamiento, puedes decir que el modelo ha hecho un buen trabajo, ya que después de 20 épocas la precisión del entrenamiento es del 99% y la pérdida del entrenamiento es bastante baja.

Sin embargo, parece que el modelo está sobreajustado, ya que la pérdida de validación es de 0,4396 y la precisión de validación es del 92%. La sobreadaptación permite intuir que la red ha memorizado muy bien los datos de entrenamiento, pero no está garantizado que funcione con datos no vistos, y por eso hay una diferencia en la precisión del entrenamiento y la validación.

Probablemente necesites ocuparte de esto. En las próximas secciones, aprenderás cómo puedes hacer que tu modelo funcione mucho mejor añadiendo una capa de Desconexión a la red y manteniendo todas las demás capas sin cambios.

Pero primero, evaluemos el rendimiento de tu modelo en el conjunto de pruebas antes de llegar a una conclusión.

Evaluación del modelo en el conjunto de pruebas

test_eval = fashion_model.evaluate(test_X, test_Y_one_hot, verbose=0)

print('Test loss:', test_eval[0])
print('Test accuracy:', test_eval[1])

('Test loss:', 0.46366268818555401)
('Test accuracy:', 0.91839999999999999)

La precisión de la prueba parece impresionante. Resulta que tu clasificador obtiene mejores resultados que el punto de referencia del que se informó aquí, que es un clasificador SVM con una precisión media de 0,897. Además, el modelo obtiene buenos resultados en comparación con algunos de los modelos de aprendizaje profundo mencionados en el perfil de GitHub de los creadores del conjunto de datos fashion-MNIST.

Sin embargo, viste que el modelo parecía sobreajustarse. ¿Son realmente tan buenos estos resultados?

Pongamos en perspectiva la evaluación de tu modelo y tracemos los gráficos de precisión y pérdida entre los datos de entrenamiento y los de validación:

accuracy = fashion_train.history['acc']
val_accuracy = fashion_train.history['val_acc']
loss = fashion_train.history['loss']
val_loss = fashion_train.history['val_loss']
epochs = range(len(accuracy))
plt.plot(epochs, accuracy, 'bo', label='Training accuracy')
plt.plot(epochs, val_accuracy, 'b', label='Validation accuracy')
plt.title('Training and validation accuracy')
plt.legend()
plt.figure()
plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.legend()
plt.show()

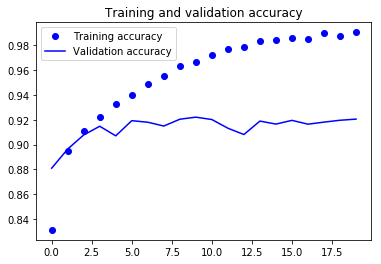
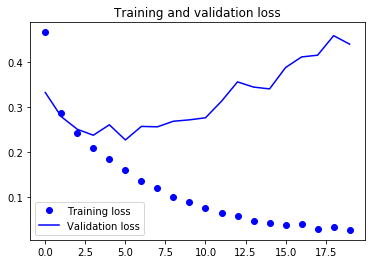
En los dos gráficos anteriores, puedes ver que la precisión de validación casi se estancó después de 4-5 épocas y rara vez aumentó en determinadas épocas. Al principio, la precisión de la validación aumentaba linealmente con la pérdida, pero luego no aumentó mucho.

La pérdida de validación muestra que se trata de un signo de sobreajuste, similar a la precisión de validación, disminuyó linealmente, pero después de 4-5 épocas, empezó a aumentar. Esto significa que el modelo intentó memorizar los datos y lo consiguió.

Teniendo esto en cuenta, es hora de introducir algo de dropout en nuestro modelo y ver si ayuda a reducir el sobreajuste.

Añadir el abandono a la red

Puedes añadir una capa de abandono para superar en cierta medida el problema del sobreajuste. El abandono desactiva aleatoriamente una fracción de neuronas durante el proceso de entrenamiento, reduciendo en cierta medida la dependencia del conjunto de entrenamiento. Cuántas fracciones de neuronas quieres desactivar lo decide un hiperparámetro, que puede ajustarse en consecuencia. De este modo, apagar algunas neuronas no permitirá que la red memorice los datos de entrenamiento, ya que no todas las neuronas estarán activas al mismo tiempo y las inactivas no podrán aprender nada.

Así que vamos a crear, compilar y entrenar de nuevo la red, pero esta vez con abandono. Y ejecútalo durante 20 épocas con un tamaño de lote de 64.

batch_size = 64
epochs = 20
num_classes = 10

fashion_model = Sequential()
fashion_model.add(Conv2D(32, kernel_size=(3, 3),activation='linear',padding='same',input_shape=(28,28,1)))
fashion_model.add(LeakyReLU(alpha=0.1))
fashion_model.add(MaxPooling2D((2, 2),padding='same'))
fashion_model.add(Dropout(0.25))
fashion_model.add(Conv2D(64, (3, 3), activation='linear',padding='same'))
fashion_model.add(LeakyReLU(alpha=0.1))
fashion_model.add(MaxPooling2D(pool_size=(2, 2),padding='same'))
fashion_model.add(Dropout(0.25))
fashion_model.add(Conv2D(128, (3, 3), activation='linear',padding='same'))
fashion_model.add(LeakyReLU(alpha=0.1))                  
fashion_model.add(MaxPooling2D(pool_size=(2, 2),padding='same'))
fashion_model.add(Dropout(0.4))
fashion_model.add(Flatten())
fashion_model.add(Dense(128, activation='linear'))
fashion_model.add(LeakyReLU(alpha=0.1))           
fashion_model.add(Dropout(0.3))
fashion_model.add(Dense(num_classes, activation='softmax'))

fashion_model.summary()

_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
conv2d_54 (Conv2D)           (None, 28, 28, 32)        320       
_________________________________________________________________
leaky_re_lu_61 (LeakyReLU)   (None, 28, 28, 32)        0         
_________________________________________________________________
max_pooling2d_52 (MaxPooling (None, 14, 14, 32)        0         
_________________________________________________________________
dropout_29 (Dropout)         (None, 14, 14, 32)        0         
_________________________________________________________________
conv2d_55 (Conv2D)           (None, 14, 14, 64)        18496     
_________________________________________________________________
leaky_re_lu_62 (LeakyReLU)   (None, 14, 14, 64)        0         
_________________________________________________________________
max_pooling2d_53 (MaxPooling (None, 7, 7, 64)          0         
_________________________________________________________________
dropout_30 (Dropout)         (None, 7, 7, 64)          0         
_________________________________________________________________
conv2d_56 (Conv2D)           (None, 7, 7, 128)         73856     
_________________________________________________________________
leaky_re_lu_63 (LeakyReLU)   (None, 7, 7, 128)         0         
_________________________________________________________________
max_pooling2d_54 (MaxPooling (None, 4, 4, 128)         0         
_________________________________________________________________
dropout_31 (Dropout)         (None, 4, 4, 128)         0         
_________________________________________________________________
flatten_18 (Flatten)         (None, 2048)              0         
_________________________________________________________________
dense_35 (Dense)             (None, 128)               262272    
_________________________________________________________________
leaky_re_lu_64 (LeakyReLU)   (None, 128)               0         
_________________________________________________________________
dropout_32 (Dropout)         (None, 128)               0         
_________________________________________________________________
dense_36 (Dense)             (None, 10)                1290      
=================================================================
Total params: 356,234
Trainable params: 356,234
Non-trainable params: 0
_________________________________________________________________

fashion_model.compile(loss=keras.losses.categorical_crossentropy, optimizer=keras.optimizers.Adam(),metrics=['accuracy'])

fashion_train_dropout = fashion_model.fit(train_X, train_label, batch_size=batch_size,epochs=epochs,verbose=1,validation_data=(valid_X, valid_label))

Train on 48000 samples, validate on 12000 samples
Epoch 1/20
48000/48000 [==============================] - 66s 1ms/step - loss: 0.5954 - acc: 0.7789 - val_loss: 0.3788 - val_acc: 0.8586
Epoch 2/20
48000/48000 [==============================] - 64s 1ms/step - loss: 0.3797 - acc: 0.8591 - val_loss: 0.3150 - val_acc: 0.8832
Epoch 3/20
48000/48000 [==============================] - 64s 1ms/step - loss: 0.3302 - acc: 0.8787 - val_loss: 0.2836 - val_acc: 0.8961
Epoch 4/20
48000/48000 [==============================] - 64s 1ms/step - loss: 0.3034 - acc: 0.8868 - val_loss: 0.2663 - val_acc: 0.9002
Epoch 5/20
48000/48000 [==============================] - 64s 1ms/step - loss: 0.2843 - acc: 0.8936 - val_loss: 0.2481 - val_acc: 0.9083
Epoch 6/20
48000/48000 [==============================] - 64s 1ms/step - loss: 0.2699 - acc: 0.9002 - val_loss: 0.2469 - val_acc: 0.9032
Epoch 7/20
48000/48000 [==============================] - 65s 1ms/step - loss: 0.2561 - acc: 0.9049 - val_loss: 0.2422 - val_acc: 0.9095
Epoch 8/20
48000/48000 [==============================] - 65s 1ms/step - loss: 0.2503 - acc: 0.9068 - val_loss: 0.2429 - val_acc: 0.9098
Epoch 9/20
48000/48000 [==============================] - 65s 1ms/step - loss: 0.2437 - acc: 0.9096 - val_loss: 0.2230 - val_acc: 0.9173
Epoch 10/20
48000/48000 [==============================] - 65s 1ms/step - loss: 0.2307 - acc: 0.9126 - val_loss: 0.2170 - val_acc: 0.9187
Epoch 11/20
48000/48000 [==============================] - 65s 1ms/step - loss: 0.2307 - acc: 0.9135 - val_loss: 0.2265 - val_acc: 0.9193
Epoch 12/20
48000/48000 [==============================] - 65s 1ms/step - loss: 0.2229 - acc: 0.9160 - val_loss: 0.2136 - val_acc: 0.9229
Epoch 13/20
48000/48000 [==============================] - 65s 1ms/step - loss: 0.2202 - acc: 0.9162 - val_loss: 0.2173 - val_acc: 0.9187
Epoch 14/20
48000/48000 [==============================] - 64s 1ms/step - loss: 0.2161 - acc: 0.9188 - val_loss: 0.2142 - val_acc: 0.9211
Epoch 15/20
48000/48000 [==============================] - 65s 1ms/step - loss: 0.2119 - acc: 0.9196 - val_loss: 0.2133 - val_acc: 0.9233
Epoch 16/20
48000/48000 [==============================] - 65s 1ms/step - loss: 0.2073 - acc: 0.9222 - val_loss: 0.2159 - val_acc: 0.9213
Epoch 17/20
48000/48000 [==============================] - 65s 1ms/step - loss: 0.2050 - acc: 0.9231 - val_loss: 0.2123 - val_acc: 0.9233
Epoch 18/20
48000/48000 [==============================] - 64s 1ms/step - loss: 0.2016 - acc: 0.9238 - val_loss: 0.2191 - val_acc: 0.9235
Epoch 19/20
48000/48000 [==============================] - 65s 1ms/step - loss: 0.2001 - acc: 0.9244 - val_loss: 0.2110 - val_acc: 0.9258
Epoch 20/20
48000/48000 [==============================] - 64s 1ms/step - loss: 0.1972 - acc: 0.9255 - val_loss: 0.2092 - val_acc: 0.9269

Vamos a guardar el modelo para que puedas cargarlo directamente y no tengas que entrenarlo de nuevo durante 20 epochs. De este modo, puedes cargar el modelo más adelante si lo necesitas y modificar la arquitectura; Alternativamente, puedes iniciar el proceso de entrenamiento sobre este modelo guardado. Siempre es una buena idea guardar el modelo -¡e incluso los pesos del modelo!- porque te ahorra tiempo. Ten en cuenta que también puedes guardar el modelo después de cada epoch para que, si ocurre algún problema que detenga el entrenamiento en una epoch, no tengas que empezar el entrenamiento desde el principio.

fashion_model.save("fashion_model_dropout.h5py")

Evaluación del modelo en el conjunto de pruebas

Por último, ¡evaluemos también tu nuevo modelo y veamos cómo funciona!

test_eval = fashion_model.evaluate(test_X, test_Y_one_hot, verbose=1)

10000/10000 [==============================] - 5s 461us/step

print('Test loss:', test_eval[0])
print('Test accuracy:', test_eval[1])

('Test loss:', 0.21460009642243386)
('Test accuracy:', 0.92300000000000004)

¡Vaya! Parece que añadir Dropout en nuestro modelo funcionó, aunque la precisión de la prueba no mejoró significativamente, pero la pérdida de la prueba disminuyó en comparación con los resultados anteriores.

Ahora, tracemos los gráficos de precisión y pérdida entre los datos de entrenamiento y validación por última vez.

accuracy = fashion_train_dropout.history['acc']
val_accuracy = fashion_train_dropout.history['val_acc']
loss = fashion_train_dropout.history['loss']
val_loss = fashion_train_dropout.history['val_loss']
epochs = range(len(accuracy))
plt.plot(epochs, accuracy, 'bo', label='Training accuracy')
plt.plot(epochs, val_accuracy, 'b', label='Validation accuracy')
plt.title('Training and validation accuracy')
plt.legend()
plt.figure()
plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.legend()
plt.show()

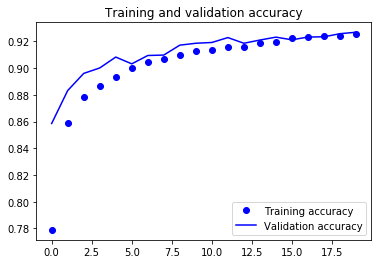
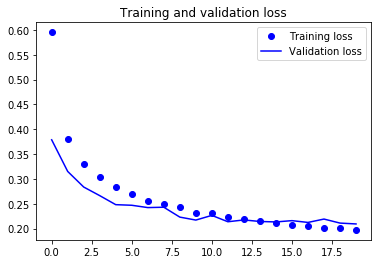
Por último, puedes ver que tanto la pérdida de validación como la precisión de validación están sincronizadas con la pérdida de entrenamiento y la precisión de entrenamiento. Aunque la pérdida de validación y la línea de precisión no son lineales, muestran que tu modelo no está sobreajustado: la pérdida de validación disminuye y no aumenta, y no hay mucha diferencia entre la precisión de entrenamiento y la de validación.

Por lo tanto, puedes decir que la capacidad de generalización de tu modelo mejoró mucho, ya que la pérdida tanto en el conjunto de prueba como en el conjunto de validación fue sólo ligeramente superior en comparación con la pérdida de entrenamiento.

Predecir etiquetas

predicted_classes = fashion_model.predict(test_X)

Como las predicciones que obtienes son valores en coma flotante, no será posible comparar las etiquetas predichas con las etiquetas de prueba verdaderas. Así, redondearás la salida que convertirá los valores flotantes en un número entero. Además, utilizarás np.argmax() para seleccionar el número de índice que tenga un valor más alto en una fila.

Por ejemplo, supongamos que la predicción para una imagen de prueba es 0 1 0 0 0 0 0 0 0 0, la salida para esto debería ser una etiqueta de clase 1.

predicted_classes = np.argmax(np.round(predicted_classes),axis=1)

predicted_classes.shape, test_Y.shape

((10000,), (10000,))

correct = np.where(predicted_classes==test_Y)[0]
print "Found %d correct labels" % len(correct)
for i, correct in enumerate(correct[:9]):
    plt.subplot(3,3,i+1)
    plt.imshow(test_X[correct].reshape(28,28), cmap='gray', interpolation='none')
    plt.title("Predicted {}, Class {}".format(predicted_classes[correct], test_Y[correct]))
    plt.tight_layout()

Found 9188 correct labels

incorrect = np.where(predicted_classes!=test_Y)[0]
print "Found %d incorrect labels" % len(incorrect)
for i, incorrect in enumerate(incorrect[:9]):
    plt.subplot(3,3,i+1)
    plt.imshow(test_X[incorrect].reshape(28,28), cmap='gray', interpolation='none')
    plt.title("Predicted {}, Class {}".format(predicted_classes[incorrect], test_Y[incorrect]))
    plt.tight_layout()

Found 812 incorrect labels

Observando unas pocas imágenes, no puedes estar seguro de por qué tu modelo no es capaz de clasificar correctamente las imágenes anteriores, pero parece que una variedad de patrones similares presentes en varias clases afectan al rendimiento del clasificador, aunque la CNN es una arquitectura robusta. Por ejemplo, las imágenes 5 y 6 pertenecen ambas a clases diferentes, pero tienen un aspecto similar, tal vez una chaqueta o quizá una camisa de manga larga.

Informe de clasificación

El informe de clasificación nos ayudará a identificar con más detalle las clases mal clasificadas. Podrás observar para qué clase ha funcionado mal el modelo de las diez clases dadas.

from sklearn.metrics import classification_report
target_names = ["Class {}".format(i) for i in range(num_classes)]
print(classification_report(test_Y, predicted_classes, target_names=target_names))

             precision    recall  f1-score   support

    Class 0       0.77      0.90      0.83      1000
    Class 1       0.99      0.98      0.99      1000
    Class 2       0.88      0.88      0.88      1000
    Class 3       0.94      0.92      0.93      1000
    Class 4       0.88      0.87      0.88      1000
    Class 5       0.99      0.98      0.98      1000
    Class 6       0.82      0.72      0.77      1000
    Class 7       0.94      0.99      0.97      1000
    Class 8       0.99      0.98      0.99      1000
    Class 9       0.98      0.96      0.97      1000

avg / total       0.92      0.92      0.92     10000

Puedes ver que el clasificador tiene un rendimiento inferior para la clase 6, tanto en precisión como en recuperación. Para la clase 0 y la clase 2, el clasificador carece de precisión. Además, para la clase 4, el clasificador carece ligeramente tanto de precisión como de recuerdo.

¡Ve más lejos!

Este tutorial fue un buen comienzo a las redes neuronales convolucionales en Python con Keras. Si has podido seguirlo fácilmente o incluso con un poco más de esfuerzo, ¡bien hecho! Intenta hacer algunos experimentos, quizá con la misma arquitectura de modelo pero utilizando diferentes tipos de conjuntos de datos públicos disponibles.

Todavía queda mucho por cubrir, así que ¿por qué no haces el curso de Aprendizaje Profundo en Python de DataCamp? Mientras tanto, asegúrate también de consultar la documentación de Keras, si aún no lo has hecho. Encontrarás más ejemplos e información sobre todas las funciones, argumentos, más capas, etc. Sin duda, ¡será un recurso indispensable cuando estés aprendiendo a trabajar con redes neuronales en Python!

Si más bien te apetece leer un libro que explique los fundamentos del aprendizaje profundo (con Keras) junto con cómo se utiliza en la práctica, sin duda deberías leer el libro Deep Learning in Python de François Chollet.