Comprender la correlación: Medir las relaciones en los datos

Si ya has explorado nuestro tutorial sobre la covarianza, sabrás que se trata de cómo cambian juntas dos variables. La correlación lleva ese concepto un paso más allá, normalizando la medida para que puedas comparar las relaciones entre distintos conjuntos de datos.

En esta guía, aprenderás qué es la correlación (en concreto, nos centraremos en la más común, llamada correlación de Pearson), en qué se diferencia de la covarianza y cómo calcularla e interpretarla utilizando Python y R. Y al final, también cubriremos distintos tipos de correlación utilizados para diferentes escenarios.

Para seguir reforzando tus conocimientos de estadística, no te pierdas nuestro programa de conocimientos Fundamentos de Estadística en Python o el curso Introducción a la Estadística en R.

¿Qué es la correlación?

La correlación mide la fuerza y la dirección de una relación lineal entre dos variables cuantitativas. Te ayuda a comprender cómo se asocian los cambios en una variable con los cambios en otra. 

Una correlación positiva significa que cuando una variable aumenta, la otra tiende a aumentar también. Una correlación negativa significa que cuando una variable aumenta, la otra tiende a disminuir.

Permíteme enumerar las ideas principales:

• La correlación cuantifica el grado en que dos variables se mueven juntas.
• El coeficiente de correlación oscila entre -1 y 1.
• Un valor de 1 indica una relación lineal positiva perfecta.
• Un valor de -1 indica una relación lineal negativa perfecta.
• Un valor de 0 indica que no hay relación lineal.

Fórmula del coeficiente de correlación de Pearson

Como ya he dicho, el coeficiente de correlación de Pearson mide la relación lineal entre dos variables continuas. Lo que yo haún no he dicho: Supone que los datos se distribuyen normalmente (en realidad, más exactamente, supone que las variables se distribuyen normalmente de forma conjunta, lo que se conoce como normalidad bivariante -algún matiz ahí-), y es sensible a los valores atípicos de . El coeficiente de correlación de Pearson se denomina r.

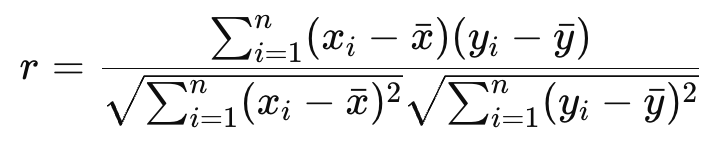
donde xi​ e yi​ son puntos de datos, y x e y son sus respectivas medias.

Coeficiente de correlación de Pearson en Python y R

Veamos cómo calcular en Python y R. 

Correlación en Python

Puedes calcular el coeficiente de correlación de Pearson en Python utilizando la función pearsonr() del módulo scipy.stats:

import numpy as np
from scipy.stats import pearsonr

# Temperature data in Celsius and corresponding Fahrenheit
temperature_celsius = np.array([0, 10, 20, 30, 40])
temperature_fahrenheit = np.array([32, 50, 68, 86, 104])  # Converted from Celsius

# Calculate Pearson correlation coefficient
correlation_coefficient, p_value = pearsonr(temperature_celsius, temperature_fahrenheit)
print("Pearson correlation coefficient:", correlation_coefficient)

Pearson correlation coefficient: 1.0
p-value: 0.0

El resultado muestra una relación lineal positiva perfecta entre x_values y y_values (ya que acabamos de definir y como 2x).

Correlación en R

En R, puedes utilizar la función cor():

temperature_celsius <- c(0, 10, 20, 30, 40)
temperature_fahrenheit <- c(32, 50, 68, 86, 104)  # Converted from Celsius

# Calculate Pearson correlation coefficient
correlation_coefficient <- cor(temperature_celsius, temperature_fahrenheit, method = "pearson")
print(correlation_coefficient)

[1] 1

Esta salida también indica una relación lineal positiva perfecta, igual que antes.

Matriz de correlaciones

Una matriz de correlaciones muestra los coeficientes de correlación entre varios pares de variables de un conjunto de datos. Es útil para explorar relaciones en datos multivariantes.

Matriz de correlación en Python

Es habitual representar la variable en un formato matricial, como un DataFrame de pandas, y calcular directamente la matriz de correlaciones:

import pandas as pd

# Create a DataFrame with two perfectly correlated variables and one that isn't
data = pd.DataFrame({
    'temperature_celsius': [0, 10, 20, 30, 40],
    'temperature_fahrenheit': [32, 50, 68, 86, 104],  # Perfect linear transformation
    'ice_cream_sales': [100, 150, 200, 220, 230]      # Roughly increasing, not perfectly
})

# Calculate the Pearson correlation matrix
correlation_matrix = data.corr(method='pearson')
print(correlation_matrix)

                      temperature_celsius  temperature_fahrenheit  ice_cream_sales
temperature_celsius              1.000000                1.000000         0.993858
temperature_fahrenheit           1.000000                1.000000         0.993858
ice_cream_sales                  0.993858                0.993858         1.000000

Esta salida muestra:

• Una correlación positiva perfecta entre temperature_celsius y temperature_fahrenheit (como era de esperar, como antes).

• Una correlación fuerte pero no perfecta entre ice_cream_sales y tanto temperature_celsius como temperature_fahrenheit.

Matriz de correlaciones en R

En R, puedes conseguir lo mismo con la función cor() que utilizamos antes, aplicada a un marco de datos o matriz:

# Create a data frame with two perfectly correlated variables and one unrelated
data <- data.frame(
  temperature_celsius = c(0, 10, 20, 30, 40),
  temperature_fahrenheit = c(32, 50, 68, 86, 104),  # Perfect conversion from Celsius
  ice_cream_sales = c(100, 150, 200, 220, 230)      # Generally increases, but not perfectly
)

# Calculate the correlation matrix
correlation_matrix <- cor(data, method = "pearson")
print(correlation_matrix)

                      temperature_celsius temperature_fahrenheit ice_cream_sales
temperature_celsius                 1.00                   1.00            0.99
temperature_fahrenheit              1.00                   1.00            0.99
ice_cream_sales                     0.99                   0.99            1.00

Esta salida de R refleja el ejemplo de Python, con:

• Correlación positiva perfecta entre temperature_celsius y temperature_fahrenheit.

• Fuerte correlación negativa entre ice_cream_sales y temperature_celsius o temperature_fahrenheit.

Este tipo de vista matricial es especialmente útil para identificarposibles multicolinealidades en la regresión o elegir variables para técnicas de reducción de la dimensionalidad como el ACP.

Correlación vs. Otras métricas

Vemos que la correlación capta las asociaciones lineales. Ahora, pongamos un poco de cuidado en distinguirla claramente de ideas que suenan parecidas.

Correlación vs. covarianza

Tanto la correlación como la covarianza miden cómo cambian juntas dos variables, pero se diferencian en dos cosas: la escala y la interpretabilidad.

• La covarianza indica la dirección de una relación lineal, pero no su fuerza de forma estandarizada. Su valor depende de las unidades de las variables, lo que dificulta la comparación entre conjuntos de datos.

• La correlación normaliza la covarianza dividiéndola por las desviaciones estándar de las variables, produciendo un valor sin unidades entre -1 y 1.

Correlación vs. R-cuadrado

R-cuadrado (R²), o coeficiente de determinación, también puede confundirse con correlación. Lo he visto especialmente cuando los analistas intentan interpretar el rendimiento de los modelos.

• La correlación ( r de Pearson) mide la fuerza y la dirección de una relación lineal entre dos variables.

• La R-cuadrado representa la proporción de varianza de una variable que es predecible a partir de otra variable en un modelo de regresión lineal. En regresión lineal simple, es el cuadrado de la r de Pearson.

Correlación vs. causalidad

¡No equipares correlación con causalidad! Se trata de un error frecuente. 

• La correlación sólo muestra que dos variables se mueven juntas. No explica por qué. Por tanto, es descriptivo, no explicativo. La correlación puede ser el resultado de una coincidencia, de variables de confusión o de causalidad inversa.

• La causalidad implica que un cambio en una variable provoca directamente un cambio en otra. Reserva la conversación sobre la causalidad a los experimentos controlados o a las técnicas de inferencia causal. 

Desafíos y errores comunes en el análisis de correlación

Es importante ser consciente de las cosas habituales en las que los analistas pueden equivocarse: 

• La correlación no implica causalidad. Hablamos de esto. 
• Los valores atípicos pueden distorsionar los coeficientes de correlación.
• Las relaciones no lineales pueden no ser bien captadas por el coeficiente de correlación de Pearson.
• Los coeficientes de correlación también son sensibles al rango de datos.

Otros tipos de coeficientes de correlación

En este artículo hemos tratado el coeficiente de correlación de Pearson, ya que es la versión de la correlación que se construyó directamente sobre el concepto de covarianza y es la medida más utilizada en la práctica. Pero ahora veamos otros tipos. 

Coeficiente de correlación de rangos de Spearman (ρ)

La correlación de rangos de Spearman evalúa la fuerza y la dirección de una relaciónmonótona utilizando valores clasificados. No es paramétrico y funciona bien para datos ordinales o tendencias no lineales pero coherentes.

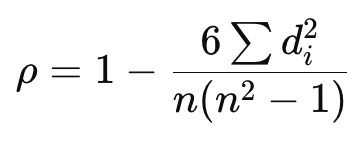
Dónde:

• di​ = la diferencia entre los rangos de cada observación
• n = el número de observaciones

Coeficiente tau de Kendall (τ)

El coeficiente tau de Kendall también mide las relaciones monótonas mediante rangos, pero se basa en el número de pares concordantes y discordantes. Es más robusto en presencia de empates y muestras pequeñas.

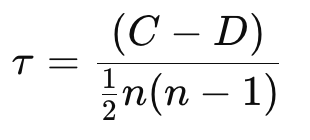
Dónde:

• C = número de parejas concordantes (parejas que están clasificadas en el mismo orden en ambas variables)
• D = número de parejas discordantes (parejas clasificadas en órdenes diferentes)
• n = número de observaciones

Conclusión

Espero que este artículo te haya resultado útil. Como has visto, la correlación es una herramienta fundamental de análisis de datos para comprender las relaciones entre variables. 

Asegúrate de seguir nuestros cursos para seguir aprendiendo. Recomiendo nuestro programa de Fundamentos de Estadística en Python o nuestro curso de Introducción a la Estadística en R como próximos pasos.