Distribución Gaussiana: Guía completa

Pocos conceptos son tan fundamentales y ampliamente aplicables en estadística y ciencia de datos como la distribución de Gauss. También conocida como distribución normal, este modelo matemático sustenta innumerables métodos estadísticos y técnicas de análisis de datos.

Esta completa guía desentraña el concepto de las distribuciones gaussianas, explorando sus propiedades, aplicaciones e importancia en el análisis moderno de datos. Examinaremos por qué son tan frecuentes en los fenómenos naturales y cómo se utilizan en diversos campos, desde las finanzas a la fabricación.

Si eres nuevo en estadística o quieres repasar los conceptos básicos, nuestro curso de Introducción a la Estadística proporciona una base excelente. Para quienes estén preparados para aplicar estos conceptos en lenguajes de programación específicos, nuestros cursos de Pensamiento Estadístico en Python (Parte 1) y Fundamentos de Estadística con R te ayudarán a apreciar las muchas formas en que aparece la distribución gaussiana en la estadística descriptiva e inferencial. 

¿Qué es una Distribución Gaussiana?

Una distribución gaussiana, también conocida como distribución normal, es una distribución de probabilidad continua caracterizada por su curva en forma de campana. Se define mediante dos parámetros:

1. μ (mu): La media o valor esperado de la distribución
2. σ (sigma): La desviación típica, que mide la dispersión de la distribución

La función de densidad de probabilidad (FDP) de una distribución gaussiana viene dada por:

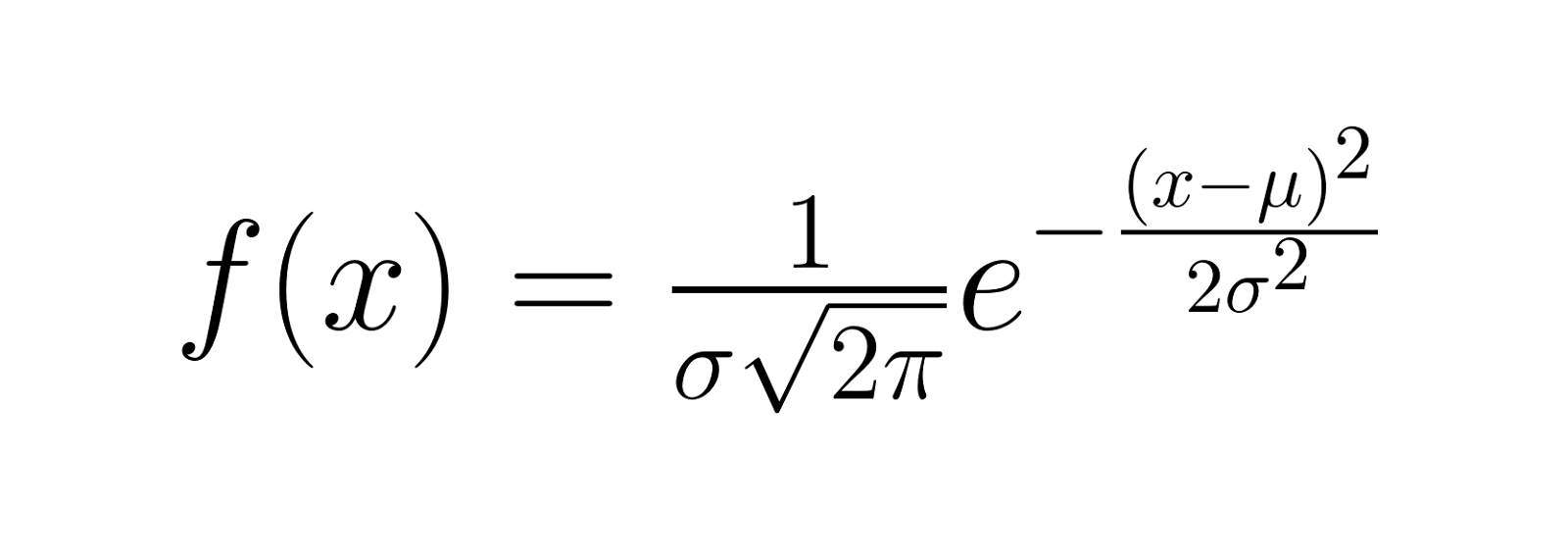
Dónde:

• x es la variable
• e es el número de Euler (aproximadamente 2,71828)
• π (pi) es la constante matemática pi (aproximadamente 3,14159)

Visualizar la distribución gaussiana

Para ilustrar el concepto de distribución gaussiana, considera la distribución del peso al nacer de los bebés nacidos a término en una gran población:

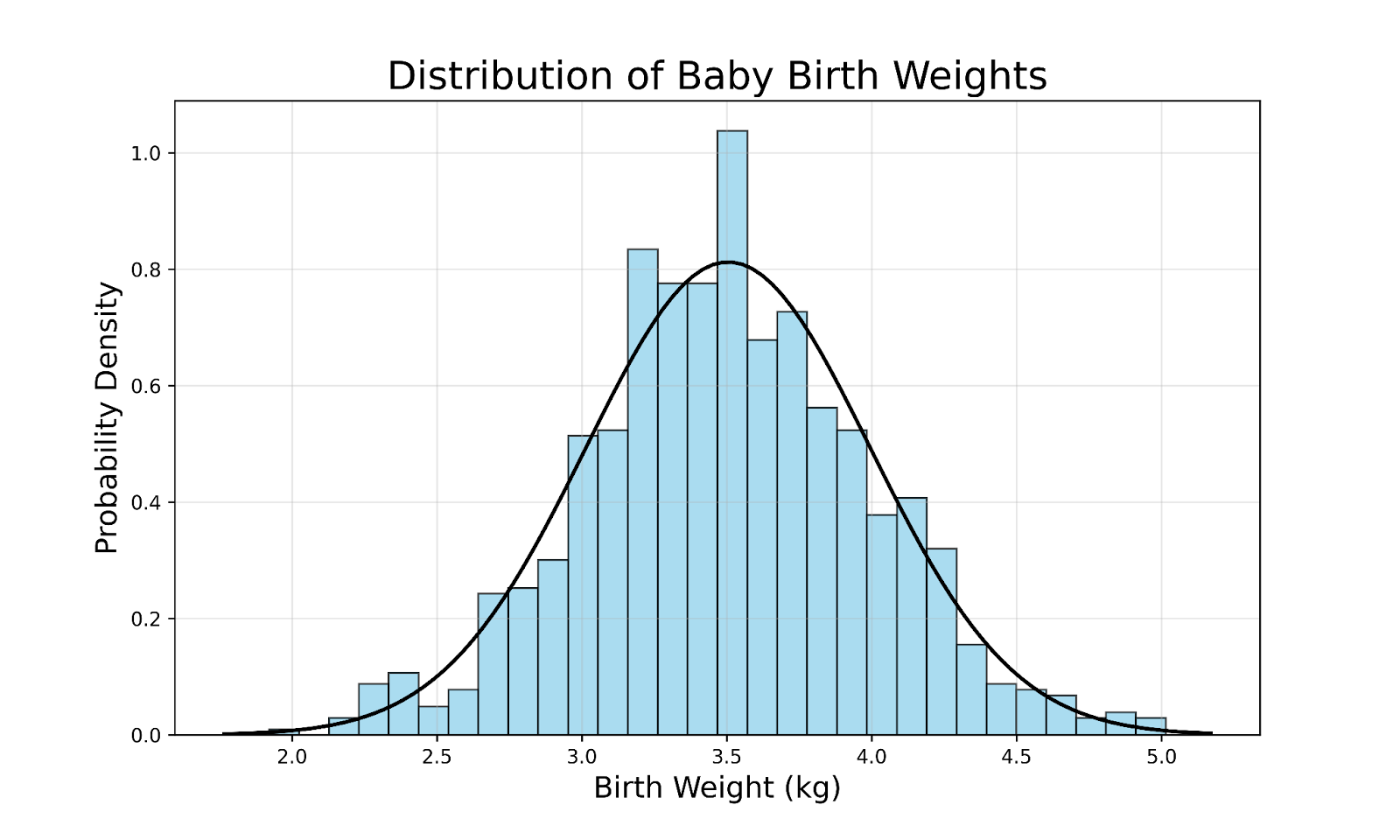
Algunas observaciones clave de este gráfico son

• El peso al nacer de la mayoría de los bebés se agrupa en torno a un valor medio (el pico de la curva).
• Menos bebés tienen pesos al nacer que se desvíen significativamente de esta media.
• Muy pocos bebés tienen pesos al nacer extremos (muy altos o muy bajos).

El teorema central del límite

El predominio de las distribuciones gaussianas en la naturaleza y la estadística puede explicarse por el teorema del límite central (CLT). La CLT establece que la distribución de las medias muestrales se aproxima a una distribución normal a medida que aumenta el tamaño de la muestra (por ejemplo, n ≥ 30), independientemente de la distribución de la población subyacente.

Un aspecto clave de la CLT es que esta convergencia a una distribución normal se produce con relativa rapidez a medida que aumenta el tamaño de la muestra. Para la mayoría de los fines prácticos, incluso muestras de tamaño moderado (por ejemplo, n ≥ 30) son suficientes para que las medias muestrales se aproximen a una distribución normal. Esto es cierto incluso si la propia población está sesgada.

La distribución gaussiana estándar

Dentro de la clase de distribuciones gaussianas, hay un caso especial conocido como distribución gaussiana estándar, también conocida más comúnmente como distribución normal estándar. Se trata de una distribución gaussiana en la que:

• La media (μ) es exactamente 0.
• La desviación típica (σ) es exactamente 1.

La función de densidad de probabilidad de una distribución gaussiana estándar viene dada por la fórmula siguiente. 

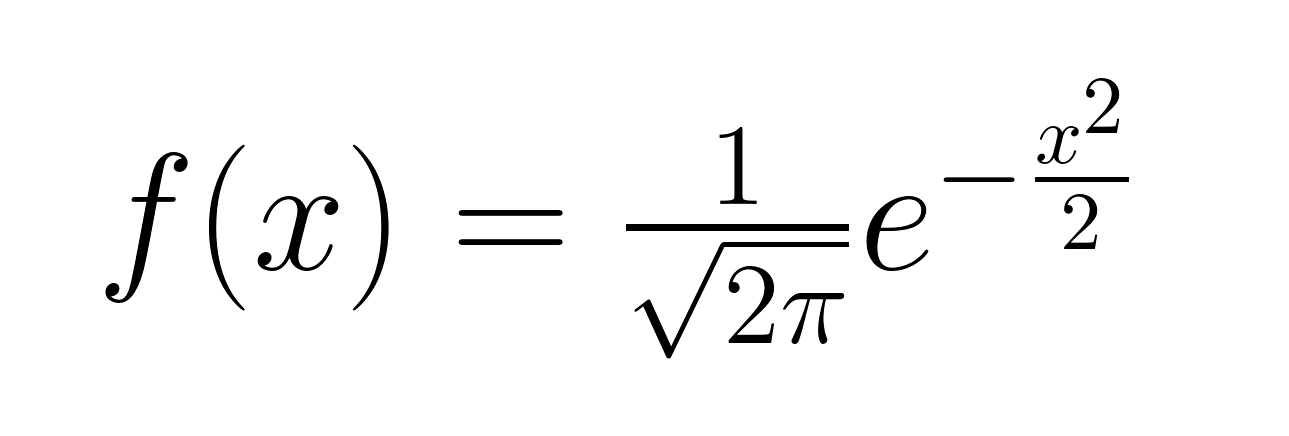
Observa que la fórmula de la función de densidad de probabilidad gaussiana estándar se simplifica a partir de la forma general debido a los valores específicos asignados a la media y a la desviación típica. Ahora, visualicemos la distribución gaussiana estándar.

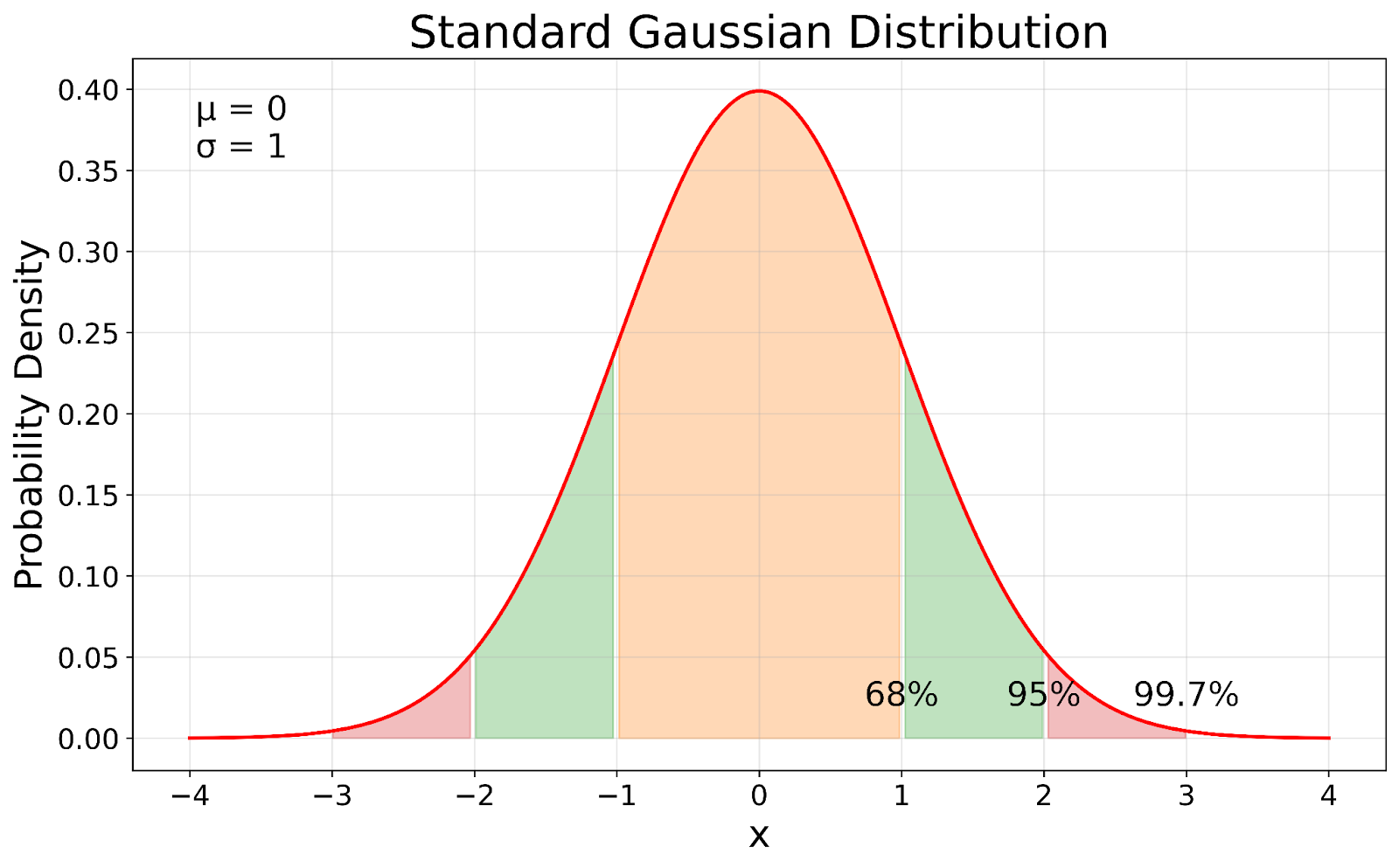gaussiana Distribución gaussiana estándar. Imagen del autor

La distribución gaussiana estándar, mostrada en nuestra visualización, sirve como punto de referencia en estadística. En nuestro visual, puedes ver cómo la Gaussiana estándar es una versión estandarizada de cualquier distribución Gaussiana. El proceso de normalización desplaza la media a 0 y escala la desviación típica a 1, conservando las propiedades fundamentales de la distribución.

Propiedades de las distribuciones gaussianas

Veamos ahora algunas de las propiedades de las distribuciones gaussianas.

Simetría y curva de campana

El sello distintivo de una distribución gaussiana es su forma de campana simétrica. Esta simetría significa que los datos tienen la misma probabilidad de caer por encima o por debajo de la media, lo que resulta especialmente útil para predecir probabilidades y hacer inferencias sobre los datos. Como se muestra en la siguiente visualización, todas las distribuciones gaussianas mantienen esta característica forma de campana, independientemente de su media o desviación típica.

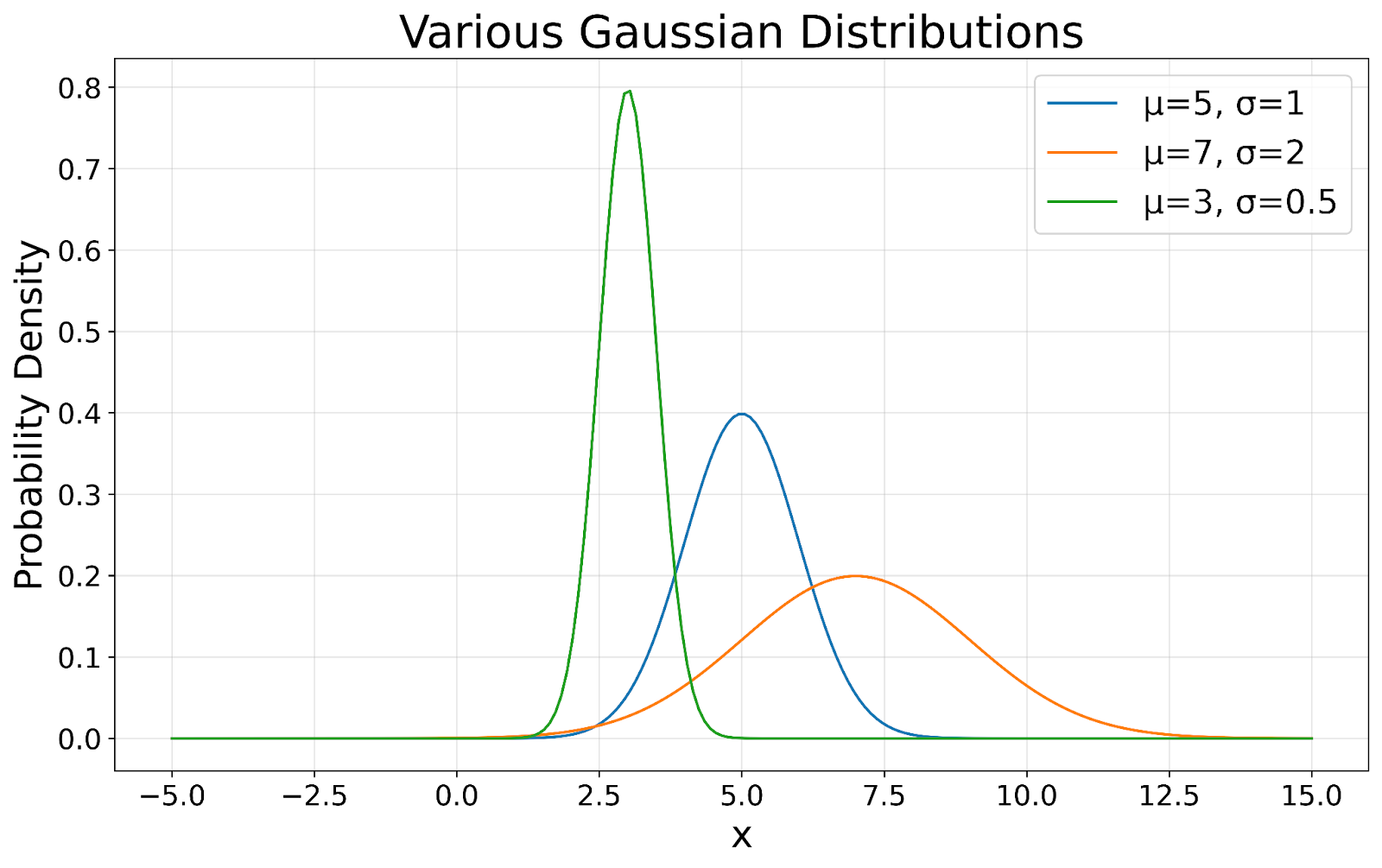gaussianas Distribuciones gaussianas visualizadas. Imagen del autor

Alineación de la media, la mediana y la moda

En una distribución gaussiana perfecta, la media (promedio), la mediana (valor medio) y la moda (valor más frecuente) son iguales. Esta alineación proporciona una indicación clara de la tendencia central de los datos, lo que resulta valioso para resumir conjuntos de datos. En nuestra visualización, puedes ver cómo el pico de cada curva representa este punto central.

Desviación típica y dispersión de datos

La desviación típica de una distribución gaussiana nos indica la dispersión de los datos respecto a la media. Sigue un patrón predecible:

• Aproximadamente el 68% de los datos están dentro de una desviación típica de la media.
• Aproximadamente el 95% se sitúa dentro de las dos desviaciones típicas.
• Aproximadamente el 99,7% se sitúa dentro de las tres desviaciones típicas.

Esta norma, conocida como regla 68-95-99,7se aplica a todas las distribuciones gaussianas, independientemente de su media o desviación típica.

Aplicaciones prácticas de las distribuciones gaussianas

Las distribuciones gaussianas son algo más que un concepto teórico: tienen amplias aplicaciones en diversos campos. 

Inferencia estadística y comprobación de hipótesis

Muchas pruebas estadísticas, como las pruebas t y ANOVA, suponen que los datos se distribuyen normalmente. Estas pruebas ayudan a los investigadores a determinar si existen diferencias significativas entre los grupos o si los efectos observados se deben probablemente al azar. El supuesto de normalidad permite a los investigadores calcular los valores p y los intervalos de confianza, proporcionando un marco para extraer conclusiones de los datos y tomar decisiones con conocimiento de causa. 

El supuesto de normalidad es tan importante que se han desarrollado técnicas de remuestreo como el bootstrapping para generar distribuciones de remuestreo de distribución normal a partir de datos no normales, lo que facilita la construcción de intervalos de confianza y la realización de otros análisis estadísticos. Nuestro tutorial sobre las pruebas de hipótesis muestra cómo realizar estas pruebas en varios escenarios, incluidas las situaciones en las que los datos se distribuyen normalmente.

Algoritmos de aprendizaje automático

Muchas técnicas de aprendizaje automático se basan en supuestos de normalidad, por lo que las distribuciones gaussianas son fundamentales para su funcionamiento e interpretación. En la regresión lineal, por ejemplo, normalmente queremos ver que los valores y (variable dependiente) siguen una distribución normal para tener confianza en nuestras estimaciones. Además, pretendemos que los residuos (las diferencias entre los valores observados y los predichos) tengan una distribución normal. Estos supuestos de normalidad sustentan las pruebas estadísticas utilizadas para evaluar la fiabilidad del modelo y los intervalos de confianza de sus predicciones.

Además, los científicos especializados en aprendizaje automático pueden preferir trabajar con datos que sigan una distribución gaussiana por razones de eficiencia computacional. Una distribución gaussiana puede contribuir indirectamente a la eficiencia computacional en determinados algoritmos, especialmente los que suponen o dependen de que los datos estén distribuidos normalmente.

• Estimación eficiente de parámetros: En una distribución gaussiana, la media y la varianza son estadísticos suficientes, lo que significa que describen completamente la distribución. Esto reduce la necesidad de un modelado complejo de los momentos superiores, acelerando la estimación de los parámetros.
• Convergencia del algoritmo: Los algoritmos como el descenso de gradiente, utilizados para la optimización en el aprendizaje automático, convergen más rápidamente si los datos se distribuyen normalmente. 
• Complejidad computacional reducida en algunos algoritmos: Algoritmos como el Bayes ingenuo gaussiano están diseñados específicamente para datos distribuidos normalmente y pueden ser computacionalmente eficientes cuando se cumple el supuesto.