R-Cuadrado Explicado: ¿En qué medida se ajusta tu modelo de regresión?

En esencia, la R-cuadrado explica la proporción de varianza de la variable dependiente que puede atribuirse a la variable (o variables) independiente(s). Podemos considerarlo como una medida de lo bien que nuestro modelo capta la historia en los datos, y cuánto queda como ruido sin explicar. Su sencillez y su interpretación directa hacen que esté muy extendido en los diagnósticos de regresión lineal, especialmente en la regresión lineal simple y múltiple.

En este artículo hablaremos del significado, el cálculo, la interpretación y los errores más comunes que rodean a la R-cuadrado, para que podamos utilizarla con confianza y cuidado. Además, veremos algunos ejemplos de fragmentos de código para calcular R-cuadrado en R y Python.

¿Qué es R-cuadrado?

El R-cuadrado, denotado como ^R², es una medida estadística de la bondad del ajuste en los modelos de regresión. Nos dice qué parte de la variación de la variable dependiente puede explicar el modelo.

El valor de R-cuadrado se sitúa entre 0 y 1:

• ^R² = 0 significa que el modelo no explica nada de la variabilidad;
• ^R² = 1 significa que el modelo lo explica todo.

Aunque el concepto es sencillo, su interpretación requiere un enfoque matizado, sobre todo cuando se pasa de la teoría a la práctica.

Cómo calcular R-cuadrado

Hay varias formas matemáticamente equivalentes de calcular la R-cuadrado, cada una de las cuales ofrece una visión diferente de lo que realmente significa "ajuste", dependiendo del contexto: regresión simple, regresión múltiple, álgebra matricial o modelización bayesiana. Exploremos el más frecuente de estos enfoques.

1. Utilizando la suma de cuadrados residual y la suma de cuadrados total

Ésta es la fórmula más estándar y utilizada:

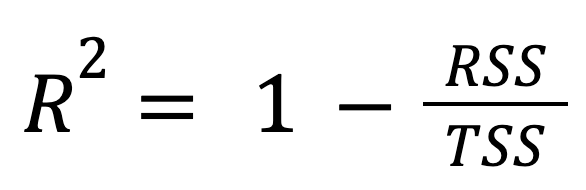
donde:

• RSS es la suma residual de cuadrados, que mide la variación no explicada por el modelo,
• SST es la suma total de cuadrados, que mide la variación total de los datos.

En otras palabras, la R-cuadrado representa la fracción de la variación total que explica el modelo. 

Este enfoque pone de manifiesto cuánto mejor funciona el modelo de regresión en comparación con la simple predicción de la media de la respuesta.

2. Utilizando la suma de cuadrados explicada y la suma de cuadrados total

El R-cuadrado también puede expresarse directamente en términos de varianza explicada:

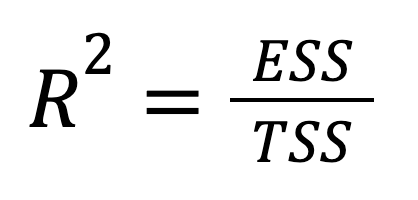
donde:

• ESS es la suma de cuadrados explicada, que mide cuánta varianza capta el modelo,
• SST es la suma total de cuadrados, que mide la variación total de los datos.

Podemos ver que esta versión hace hincapié en qué parte de la variación total del resultado es captada por las predicciones del modelo. En otras palabras, aquí el centro de atención se desplaza de lo que no conseguimos explicar (RSS) a lo que sí logramos (ESS), proporcionando un encuadre más optimista.

Para profundizar en los tres componentes de la suma de cuadrados, lee Comprender la suma de cuadrados: Guía de la TSM, la TSS y la TSE.

3. Utilizando la suma de cuadrados explicada y la suma de cuadrados residual

En el contexto de una tabla ANOVA, la R-cuadrado surge naturalmente de la descomposición de la variabilidad total: 

donde:

• ESS es la suma de cuadrados explicada, que mide cuánta varianza capta el modelo,
• RSS es la suma residual de cuadrados, que mide la variación no explicada por el modelo.

Esta formulación muestra qué parte de la varianza total recoge el modelo y qué parte queda sin explicar.

Esta perspectiva es un poco única porque vincula la R-cuadrado a la comprobación de hipótesis. Esto se debe a que la relación entre ESS y RSS se utiliza para calcular el estadístico F de , lo que hace que el R-cuadrado sea una parte importante de las pruebas de significación en los informes tipo ANOVA.

4. Uso del coeficiente de correlación en la regresión lineal simple

Los tres últimos métodos eran fórmulas algebraicamente equivalentes derivadas de la descomposición de la regresión. He aquí una nueva perspectiva:

En la regresión lineal simple con un solo predictor, la R-cuadrado tiene un atajo:

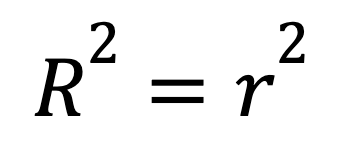
donde

• r es el coeficiente de correlación de Pearson entre x e y.

Esta fórmula muestra cómo una fuerte relación lineal entre dos variables se traduce directamente en un elevado R-cuadrado. 

Para comprender la teoría subyacente a la regresión lineal simple, consulta Regresión lineal simple: Todo lo que necesitas saber.

5. Utilizando el error cuadrático medio y la varianza del resultado

El R-cuadrado puede calcularse como una medida normalizada del error del modelo: 

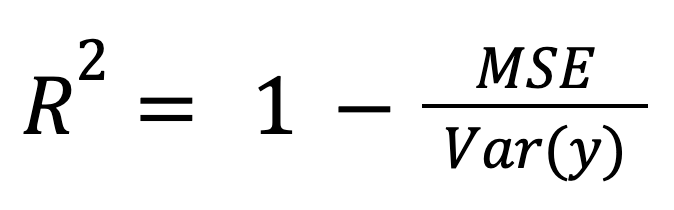
donde:

• MSE es el error cuadrático medio del modelo,
• Var(y) es la varianza del resultado verdadero.

Este encuadre es especialmente relevante cuando se comparan modelos entre diferentes escalas o unidades, porque normaliza el error del modelo según la dispersión general de los datos.

6. Utilizando la varianza de los valores predichos

Suponiendo que los residuos no estén correlacionados con las predicciones, R-cuadrado también puede interpretarse como la fracción de varianza captada por el modelo:

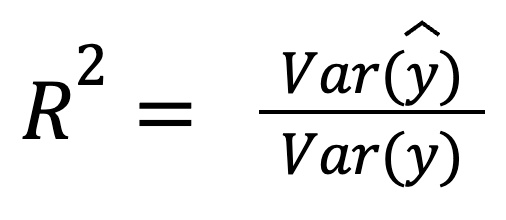
donde:

• Var(ŷ) es la varianza de las predicciones del modelo,
• Var(y) es la varianza del resultado verdadero.

Esta versión pone de relieve lo bien que las propias predicciones reflejan la dispersión de los datos reales.

Interpretación de R-cuadrado

Como hemos mencionado antes, la R-cuadrado es fácil de calcular, pero un poco más complicada de interpretar de forma significativa.

• Un elevado R-cuadrado significa que el modelo explica una gran parte de la varianza. Sin embargo, eso no significa que nuestro modelo sea necesariamente correcto o útil.
• Un R-cuadrado bajo significa que el modelo explica poca varianza. Esto no siempre es malo, sobre todo en ciencias sociales o en datos ruidosos, donde a menudo se espera una R-cuadrado baja.

Es importante recordar que la R-cuadrado mide la correlación, pero no la causalidad. Que nuestros predictores expliquen el resultado no significa que locausen, porque correlación sigue sin significar causalidad. Además, la R-cuadrado no indica si las predicciones son exactas.

Aquí tienes dos recursos útiles sobre temas más avanzados relacionados con la regresión lineal: 

• Factor de Inflación de la Varianza (VIF): Cómo abordar la multicolinealidad en el análisis de regresión
• Descomposición QR en machine learning: Guía detallada

Cuándo utilizar R-cuadrado

La R-cuadrado puede ser muy útil si se utiliza en las situaciones adecuadas. Es apropiado para:

• Comparar modelos con el mismo número de predictores.
• Explicar cuánta varianza de un conjunto de datos explica el modelo.

Por otra parte, la R-cuadrado puede ser engañosa en los siguientes supuestos:

• Añadir predictores irrelevantes, lo que provoca un sobreajuste. En este caso, la R-cuadrado siempre aumenta aunque no mejore el rendimiento predictivo del modelo.
• Comparar modelos con distintos números de predictores, es decir, con distintas complejidades. En este caso, la R-cuadrado ajustada es una mejor opción. Hablaré más adelante de la R-cuadrado ajustada.

Ejemplos de R-cuadrado en R y Python

Ilustremos ahora el concepto de R-cuadrado en R y Python utilizando el conjunto de datos Kaggle de la Lonja. En ambos lenguajes de programación, construiremos dos modelos:

• Modelo 1: Predecir el peso de los peces utilizando cuatro predictores.
• Modelo 2: Añade un predictor aleatorio e irrelevante.

R ejemplo

Empecemos por R.

Modelo 1

# Load data
fish <- read.csv("Fish.csv")

# Model 1
model1 <- lm(Weight ~ Length1 + Length2 + Height + Width, data=fish)
summary(model1)$r.squared

Salida:

[1] 0.8673

Modelo 2

# Model 2 with an irrelevant predictor
fish$random_noise <- rnorm(nrow(fish))
model2 <- lm(Weight ~ Length1 + Length2 + Height + Width + random_noise, data=fish)
summary(model2)$r.squared

Salida:

[1] 0.8679

Como vemos, la R-cuadrado aumenta ligeramente tras añadir un predictor irrelevante (Modelo 2). Sin embargo, eso no significa que el modelo haya mejorado. Al fin y al cabo, sólo hemos añadido ruido aleatorio.

Para leer más sobre el tema, consulta los siguientes tutoriales:

• Cómo hacer una regresión lineal en R
• Regresión lineal múltiple en R: Tutorial con ejemplos

Y recuerda matricularte en nuestro curso designado:

• Curso de Introducción a la Regresión en R

Ejemplo en Python

Ahora, probemos en Python.

Modelo 1

import pandas as pd
import statsmodels.api as sm
import numpy as np

# Load data
fish = pd.read_csv('Fish.csv')
X1 = fish[['Length1', 'Length2', 'Height', 'Width']]
y = fish['Weight']

# Model 1
X1 = sm.add_constant(X1)
model1 = sm.OLS(y, X1).fit()
print(model1.rsquared)

Salida:

0.8673

Modelo 2

# Model 2 with an irrelevant predictor
fish['random_noise'] = np.random.randn(len(fish))
X2 = fish[['Length1', 'Length2', 'Height', 'Width', 'random_noise']]
X2 = sm.add_constant(X2)
model2 = sm.OLS(y, X2).fit()
print(model2.rsquared)

Salida:

0.8679

De nuevo, observamos un ligero aumento del valor R-cuadrado, pero esto no es más que la captura de ruido aleatorio.

Para seguir aprendiendo, inscríbete en nuestros cursos:

• Introducción a la regresión con modelos estadísticos en Python y
• Regresión intermedia con modelos estadísticos en Python

R-Cuadrado vs. Métricas relacionadas

Ahora compararemos brevemente la R-cuadrado con dos métricas relacionadas: la R-cuadrado ajustada y la R-cuadrado predicha.

R-cuadrado vs. R-cuadrado ajustado

A diferencia de la R-cuadrado, la R-cuadrado ajustada tiene en cuenta el número de predictores. En concreto, penaliza al modelo por incluir predictores innecesarios:

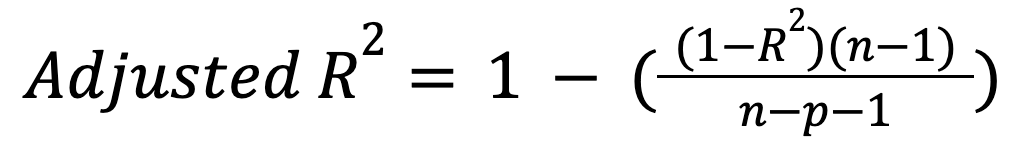
donde:

• n es el número de observaciones,
• p es el número de predictores.

Esta métrica sólo aumenta si un nuevo predictor mejora realmente el modelo de forma significativa, y puede disminuir en el caso contrario. Lee nuestro tutorial para saber más sobre esta importante extensión: R-cuadrado ajustado: Una explicación clara con ejemplos.

R-cuadrado frente a R-cuadrado previsto

Mientras que el R-cuadrado normal muestra el rendimiento del modelo con los datos de entrenamiento, el R-cuadrado predicho nos indica su rendimiento con datos nuevos, no vistos. Por tanto, esta métrica evalúa la capacidad de generalización del modelo.

El R-cuadrado previsto se calcula mediante validación cruzada o reteniendo parte de los datos de entrenamiento para realizar más pruebas. Puede ser significativamente inferior al R-cuadrado normal si el modelo está sobreajustado. Por tanto, un escenario en el que obtengamos un valor alto de R-cuadrado regular pero un valor bajo de R-cuadrado predicho puede indicar muy probablemente un sobreajuste del modelo.

Errores comunes sobre R-cuadrado

Echemos un vistazo a algunos mitos populares sobre R-cuadrado, junto con el verdadero estado de las cosas: 

• "Un R-cuadrado alto siempre significa un buen modelo". Esto no es necesariamente cierto. La R-cuadrado puede ser alta para un modelo sobreajustado o construido sobre correlaciones espurias. Naturalmente, en ambos casos, el modelo no puede calificarse de bueno.
• "R-cuadrado mide el poder predictivo". En realidad, sólo mide el ajuste del modelo en los datos de entrenamiento y no dice nada sobre los datos no vistos. Para evaluar el rendimiento futuro del modelo, necesitamos otras métricas como la R-cuadrado pronosticada antes mencionada.
• "Siempre debemos aspirar a un R-cuadrado elevado". Bueno, no siempre. Depende del ámbito, así como de la propia calidad de los datos. Como hemos mencionado anteriormente en este artículo, para las ciencias sociales como la psicología o la historia, el valor de R-cuadrado puede ser muy bajo (0,1 o incluso menos) y seguir siendo significativo. Lo mismo ocurre con los datos ruidosos, en los que se espera un valor bajo de R-cuadrado.

Conclusión

En resumen, hemos aprendido qué es la R-cuadrado, cómo calcular esta métrica (tanto matemáticamente como en R y Python), cuándo utilizarla y cuándo evitarla, y cómo interpretar los resultados. Además, tocamos dos métricas relacionadas y algunos conceptos erróneos muy extendidos sobre R-cuadrado. 

En pocas palabras, la R-cuadrado es una medida útil, intuitiva y directa del ajuste de un modelo de regresión. Es un buen punto de partida para la evaluación de modelos, pero debe utilizarse con prudencia, interpretarse junto con otras métricas y no confundirse con el cuadro completo. Esto es especialmente cierto en contextos de regresión múltiple y selección de modelos.