Comprender la Distribución Exponencial: Guía completa

Comprender las distribuciones de probabilidad es fundamental para la ciencia de datos, y entre ellas, la distribución exponencial me parece una con algunas características únicas que merece la pena explorar. Aunque comparte conexiones matemáticas con la distribución de Poisson, la distribución exponencial modela de forma única los intervalos de tiempo entre sucesos en lugar del recuento de sucesos. 

Para los que se inician en los conceptos de probabilidad, nuestro curso Fundamentos de la Probabilidad en Python proporciona conocimientos básicos esenciales. Las aplicaciones prácticas de la distribución exponencial se extienden a diversos ámbitos, desde la ingeniería de fiabilidad a la teoría de colas, lo que la hace especialmente valiosa en campos como el análisis de supervivencia, que se explora en profundidad en Análisis de supervivencia en Python. Esta guía explorará los conceptos fundamentales, los fundamentos matemáticos y las aplicaciones en el mundo real de la distribución exponencial, dotándote de los conocimientos necesarios para aplicarla eficazmente en tus proyectos de ciencia de datos.

¿Qué es la Distribución Exponencial?

La distribución exponencial es una distribución de probabilidad continua que modela el tiempo entre sucesos en un proceso en el que los sucesos ocurren de forma continua e independiente a una tasa media constante. Es especialmente útil para analizar situaciones que implican tiempos de espera, tiempos de vida e intervalos entre sucesos.

Imagina que trabajas en un ajetreado centro de atención al cliente. El tiempo entre llamadas entrantes de clientes suele seguir una distribución exponencial. Del mismo modo, en la fabricación, el tiempo que transcurre hasta que una máquina falla o necesita mantenimiento suele mostrar un comportamiento exponencial.

Características principales de la distribución exponencial

La distribución exponencial tiene varias propiedades únicas que la hacen especialmente útil en aplicaciones del mundo real:

La propiedad sin memoria

Ésta es quizá la característica más distintiva de la distribución exponencial. Significa que el comportamiento futuro del sistema no depende de su historia pasada. Por ejemplo, si una bombilla ya ha durado 1000 horas, la probabilidad de que dure otras 100 horas es la misma que si fuera nueva. Esta propiedad es exclusiva de la distribución exponencial entre las distribuciones continuas.

Tasa de riesgo constante

La distribución exponencial mantiene una tasa de fallos constante a lo largo del tiempo. Esto significa que la probabilidad de que se produzca un suceso en el siguiente pequeño intervalo de tiempo sigue siendo la misma, independientemente del tiempo que haya transcurrido.

La relación entre las distribuciones exponencial y de Poisson es fundamental en la teoría de la probabilidad. Mientras que la distribución de Poisson modela el número de sucesos que ocurren en un intervalo de tiempo fijo, la distribución exponencial modela el tiempo entre esos sucesos. Son dos caras de la misma moneda: si los sucesos ocurren según un proceso de Poisson con tasa λ, entonces el tiempo de espera entre sucesos sigue una distribución exponencial con parámetro λ.

Formulación matemática

La distribución exponencial está definida por un único parámetro λ (lambda), que representa el parámetro de la tasa. Veamos sus componentes matemáticos clave:

Función de densidad de probabilidad (PDF)

La PDF nos ayuda a calcular la probabilidad de que se produzca un suceso en un intervalo determinado. La PDF de la distribución exponencial es la siguiente:   

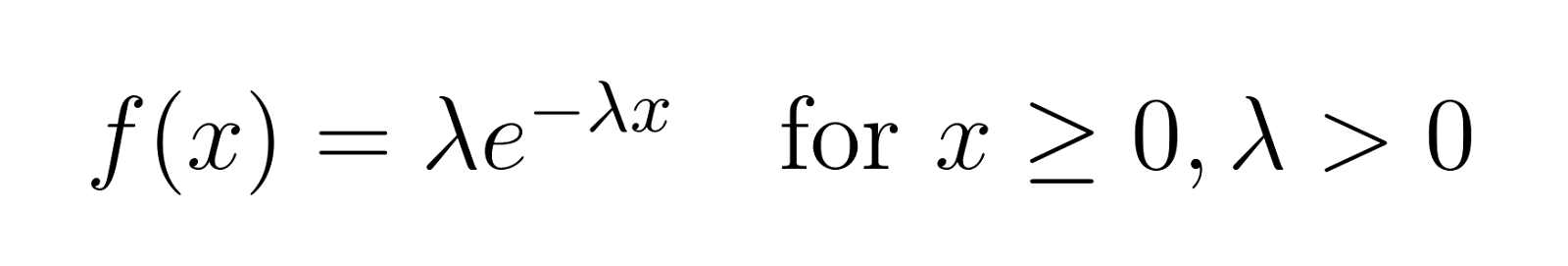
   donde:

• x es la variable aleatoria (normalmente representa el tiempo)
• λ es el parámetro de la tasa (λ > 0)
• e es el número de Euler (aproximadamente 2,71828)

Función de distribución acumulativa (FDA)

La FCD es especialmente útil cuando queremos hallar la probabilidad de que un suceso ocurra antes de un tiempo determinado. Nos da la probabilidad de que el tiempo de espera sea menor o igual que un valor determinado. Aquí tienes la FDA de la distribución exponencial:

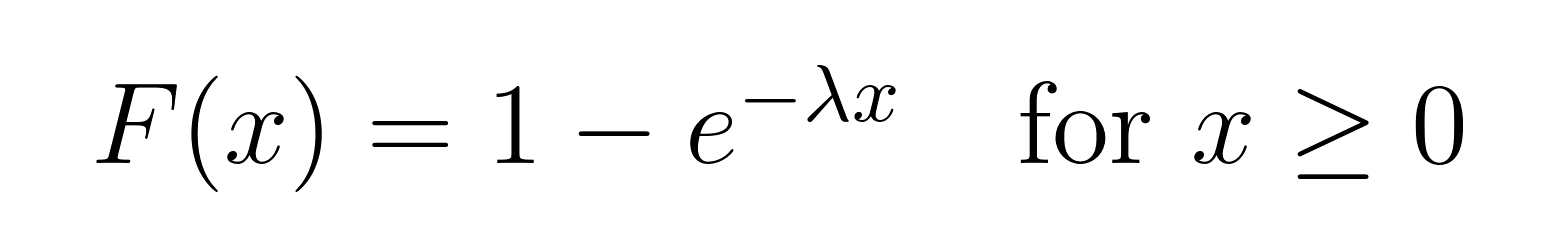
Aplicaciones de la distribución exponencial

La distribución exponencial desempeña un papel vital en diversos campos, ayudándonos a modelar y comprender los procesos dependientes del tiempo. Exploremos algunas de sus principales aplicaciones. 

Ingeniería de fiabilidad

La ingeniería de la fiabilidad se basa en gran medida en la distribución exponencial para modelar la vida útil de componentes y sistemas. Esto es especialmente útil por la propiedad "sin memoria" de la distribución: la vida futura de un componente depende sólo del presente, no del tiempo que lleve funcionando.

Por ejemplo, los componentes electrónicos suelen presentar tiempos de fallo distribuidos exponencialmente, lo que demuestra la propiedad única sin memoria de esta distribución. Esto significa que un microprocesador nuevo tiene la misma probabilidad de fallar en la hora siguiente que uno que lleve funcionando un mes (suponiendo que no haya efectos de desgaste). Los fabricantes de hardware para servidores utilizan ampliamente esta distribución en sus análisis de fiabilidad para calcular el Tiempo Medio Entre Fallos (MTBF), determinar los programas de mantenimiento óptimos y predecir los costes de garantía y las necesidades de sustitución. Esta información es valiosa tanto para el desarrollo de productos como para la planificación empresarial.

Teoría de colas

En la teoría de colas, la distribución exponencial es fundamental para modelar el tiempo entre llegadas o los tiempos de servicio en muchos sistemas. Esta aplicación es especialmente útil en:

1. Centros de Atención al Cliente:

• Tiempo de modelado entre llamadas entrantes
• Predecir los picos de carga
• Optimizar la programación del personal

2. Telecomunicaciones:

• Analizar los patrones de tráfico de la red
• Modelización de los tiempos de llegada de paquetes en redes de datos
• Planificación de la capacidad de la red

3. Sistemas sanitarios:

• Modelización de los tiempos de llegada de los pacientes a los servicios de urgencias
• Estimación de los tiempos de espera de los servicios
• Planificación de la asignación de recursos

La distribución exponencial funciona bien en estos contextos porque muchos procesos de llegada pueden aproximarse como sucesos sin memoria que ocurren a una tasa media constante.

Cálculo de probabilidades con la distribución exponencial

Cuando trabajamos con la distribución exponencial, tenemos dos enfoques principales para calcular probabilidades: la FDP es especialmente útil cuando necesitamos hallar la probabilidad de que un suceso ocurra dentro de un intervalo o rango específico, mientras que la FCD nos ayuda a determinar la probabilidad de que un suceso ocurra antes de un momento determinado. Exploremos ambos enfoques utilizando un escenario práctico de servicio de asistencia.

Utilizando la función de densidad de probabilidad

Hemos mencionado que la PDF nos ayuda a calcular la probabilidad de que un suceso ocurra en un intervalo. Para distribuciones continuas como la exponencial, tenemos que integrar la FDP en el intervalo de interés.

Veamos un ejemplo práctico: Imagina que estamos analizando las llamadas de atención al cliente en un servicio de asistencia, donde las llamadas llegan siguiendo una distribución exponencial con una tasa media de 3 llamadas por hora (λ = 3).

Para hallar la probabilidad de esperar entre 10 y 20 minutos a la siguiente llamada, haríamos:

1. Convierte el tiempo en horas: (10 minutos = 1/6 de hora, 20 minutos = 1/3 de hora)
2. Utiliza la fórmula: P(1/6 < X < 1/3) = ∫[1/6 a 1/3] 3e^(-3x)dx
3. Evalúa: = -e^{(-3x)|[1/6 a 1/3]}
4. Calcula: = [e^(-0,5) - e^(-1)] ≈ 0,2325 o aproximadamente 23,25%.

Utilizando la función de distribución acumulativa

Dijimos que la FCD es útil cuando queremos hallar la probabilidad de un suceso antes de un tiempo. Ahora, utilizando nuestro ejemplo del servicio de asistencia: ¿Cuál es la probabilidad de que recibamos una llamada en los primeros 15 minutos?

Utilizando nuestro ejemplo del servicio de asistencia: ¿Cuál es la probabilidad de que recibamos una llamada en los primeros 15 minutos?

1. Convierte 15 minutos en horas: (15 minutos = 1/4 de hora)
2. Utiliza la fórmula CDF: F(1/4) = 1 - e^(-3*1/4)
3. Calcula: = 1 - e^(-0,75) ≈ 0,5276 o alrededor del 52,76%^.

Esto significa que hay aproximadamente un 53% de posibilidades de recibir una llamada en los primeros 15 minutos. Observa cómo la FCD hace que estos cálculos de probabilidad "hasta" sean más sencillos que utilizar la FDP.

Visualizar la distribución exponencial

Veamos primero la distribución exponencial por sí misma y luego comparémosla con otras distribuciones.

Representación gráfica

Aquí tienes un conjunto de gráficos que he creado en Python:

Exploremos cómo las fórmulas matemáticas se traducen en patrones visuales. La visualización muestra tres parámetros de tasa diferentes (0,5, 1,0 y 2,0) para demostrar cómo λ da forma a la distribución:

Mirando el PDF (gráfico superior):

• Cuando λ = 2,0 (línea verde), vemos el descenso inicial más pronunciado, que comienza en f(0) = 2,0. Esto indica que es mucho más probable que los primeros acontecimientos
• Cuando λ = 1,0 (línea naranja), obtenemos la distribución exponencial estándar con un decaimiento más moderado
• Cuando λ = 0,5 (línea roja), la curva desciende más gradualmente, mostrando que los tiempos de espera más largos son más comunes

La FCD (gráfico inferior) cuenta una historia complementaria:

• La tasa más alta (λ = 2,0) da lugar al aumento más pronunciado, lo que demuestra que la probabilidad acumulada se acumula rápidamente
• La tasa más baja (λ = 0,5) muestra una acumulación más gradual de la probabilidad
• Todas las curvas acaban aproximándose a 1, lo que ilustra que la probabilidad de que se produzca el acontecimiento se aproxima a la certeza a medida que aumenta el tiempo

Este comportamiento hace que la distribución exponencial sea especialmente útil para modelizar fenómenos del mundo real, como los tiempos de espera, la vida útil de los equipos y el tiempo entre sucesos en un proceso de Poisson.

Comparación con otras distribuciones

Las características únicas de la distribución exponencial quedan más claras cuando se compara con otras distribuciones de probabilidad comunes. Examinemos estas comparaciones a través de nuestra visualización:

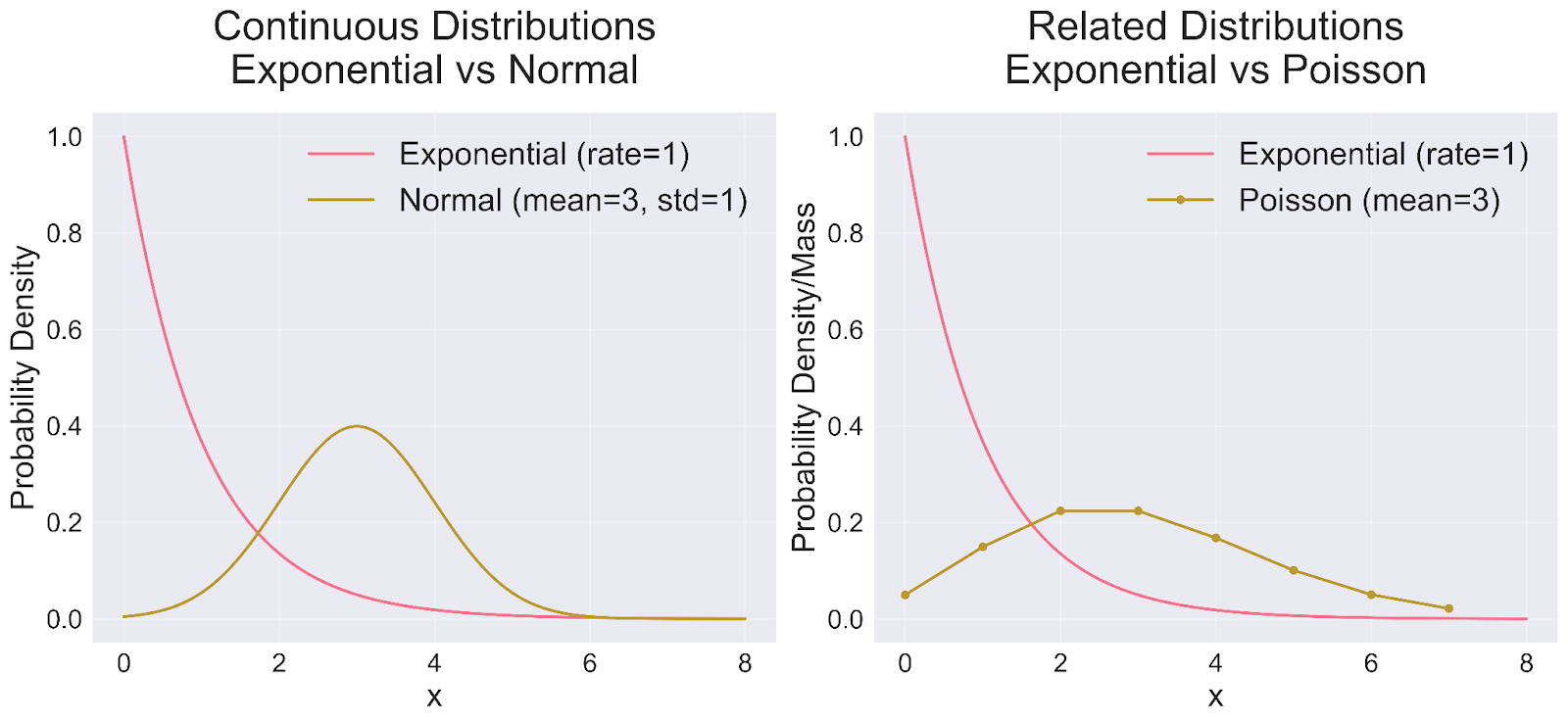
Al examinar la comparación de la distribución normal (panel izquierdo), surgen varias diferencias clave. La distribución exponencial muestra un pronunciado sesgo a la derecha, alcanzando su valor máximo inmediatamente antes de declinar de forma continua. Esto contrasta fuertemente con la conocida curva simétrica en forma de campana de la distribución normal, centrada en su valor medio. Aunque ambas se consideran distribuciones continuas, sirven para fines de modelización distintos: la distribución exponencial destaca en la modelización de tiempos de espera e intervalos, mientras que la distribución normal suele ocuparse de medidas y promedios.

La relación con la distribución de Poisson (panel derecho) revela otra dimensión fascinante de la teoría de la probabilidad. Mientras que la distribución exponencial mide el tiempo entre sucesos, la distribución de Poisson se centra en contar el número de sucesos dentro de un intervalo fijo. Estas distribuciones forman dos caras de la misma moneda: en un proceso de Poisson, los tiempos de espera siguen naturalmente una distribución exponencial. Otra distinción notable radica en su continuidad: la distribución exponencial puede tomar cualquier valor real positivo, mientras que la distribución de Poisson trata exclusivamente con enteros discretos no negativos.

Estas ideas comparativas aclaran por qué la distribución exponencial destaca en determinados escenarios de modelización. Resulta inestimable cuando se analizan intervalos de tiempo entre sucesos aleatorios, ya que ofrece capacidades que van más allá del enfoque de recuento de sucesos de la distribución de Poisson. La distribución brilla especialmente en escenarios que exigen una evaluación inmediata de la probabilidad de ocurrencia, en contraste con el enfoque de tendencia central de la distribución normal. Quizá lo más distintivo sea que su propiedad única de carecer de memoria la diferencia de las distribuciones Normal y Poisson, lo que la convierte en la elección óptima para procesos en los que los sucesos pasados no influyen en las probabilidades futuras.

Errores y trampas habituales

Al trabajar con la distribución exponencial, varios errores comunes pueden conducir a un análisis incorrecto. Comprender estos posibles escollos ayuda a garantizar una aplicación precisa de la distribución en situaciones reales.

Interpretación errónea de la propiedad sin memoria

La propiedad de no tener memoria suele causar confusión porque parece contradecir nuestra experiencia cotidiana. He aquí algunos malentendidos comunes y sus correcciones:

Un error frecuente es pensar que la propiedad de ausencia de memoria significa que los acontecimientos pasados no tienen valor para la predicción. En realidad, significa que la probabilidad de esperar un periodo de tiempo adicional sigue siendo la misma, independientemente del tiempo que ya hayas esperado. Por ejemplo:

• Interpretación incorrecta: "Si una bombilla sigue una distribución exponencial y no ha fallado en 5 años, debe estar a punto de fallar pronto".
• Interpretación correcta: "Si una bombilla sigue una distribución exponencial y no ha fallado en 5 años, su probabilidad de durar otro año es la misma que la de que una bombilla nueva dure un año".

Otro error consiste en suponer que todos los escenarios de fiabilidad presentan la propiedad de ausencia de memoria. En realidad, muchos sistemas muestran efectos de envejecimiento o patrones de desgaste que no siguen un comportamiento exponencial. Por ejemplo, los componentes mecánicos suelen presentar tasas de fallo crecientes con el paso del tiempo.

Uso incorrecto de los parámetros

Se producen varios errores comunes al seleccionar y aplicar el parámetro tasa:

1. Tasa frente a confusión media:

   • Un error común es utilizar el valor medio como parámetro de la tasa (λ)

   • Recuerda: La media (valor esperado) es en realidad 1/λ

   • Por ejemplo, si los acontecimientos se producen por término medio cada 2 horas, λ = 1/2, no 2

2. Desajuste de la unidad:

   • El parámetro de velocidad debe ser coherente con las unidades de tiempo de tus datos

   • Si mides el tiempo en horas pero especificas λ en días^(-1), tus probabilidades serán incorrectas

   • Convierte siempre a unidades coherentes antes de aplicar la distribución

3. Aplicación excesiva:

   • Verosimilitud de que los acontecimientos ocurren independientemente

   • Que la tasa permanezca constante a lo largo del tiempo

   • Y que el proceso no tiene efectos de memoria 

Para evitar estos errores, define siempre claramente tus unidades y conviértelas de forma coherente, verifica que los supuestos de la distribución exponencial se ajustan a tu escenario, comprueba que tus datos tienen un comportamiento exponencial antes de aplicar la distribución y documenta tus elecciones de parámetros y su justificación.

Conclusión

La elegante simplicidad de la distribución exponencial y sus potentes aplicaciones la convierten en una herramienta indispensable en el conjunto de herramientas de un científico de datos. Su propiedad única de no tener memoria y su relación con otras distribuciones, en particular la distribución de Gauss, ponen de relieve su lugar especial en la teoría de la probabilidad.

Aunque esta guía ha cubierto los aspectos esenciales, siempre hay algo más que explorar en aplicaciones especializadas. Para los interesados en implementaciones prácticas, nuestro curso Simulación Estadística en Python ofrece experiencia práctica con estos conceptos. Además, comprender cómo se relaciona la distribución exponencial con otras distribuciones de probabilidad, como se detalla en Distribuciones de probabilidad multivariantes en R, proporciona una perspectiva más amplia sobre su papel en la modelización estadística. Ya estés analizando datos de supervivencia, modelando la fiabilidad de un sistema o estudiando el comportamiento de las colas, dominar la distribución exponencial abre nuevas posibilidades en el análisis de datos y la modelización estadística.