Curso
En estadística y ciencia de datos, la distribución de Poisson es una herramienta importante para modelar sucesos discretos que ocurren en un intervalo fijo. Llamada así por el matemático francés Siméon Denis Poisson, esta distribución de probabilidad ayuda a analizar y predecir sucesos raros, lo que la hace valiosa para los profesionales de los datos en diversos campos.
Si eres nuevo en estadística, nuestro curso de Introducción a la Estadística proporciona una base sólida para comprender estos conceptos. Para quienes estén preparados para aprender de verdad la teoría de la probabilidad, el curso Fundamentos de la Probabilidad en Python ofrece una exploración exhaustiva de los conceptos probabilísticos, incluida la distribución de Poisson.
¿Qué es una Distribución de Poisson?
La distribución de Poisson es una distribución de probabilidad discreta que expresa la probabilidad de que se produzca un número determinado de sucesos en un intervalo fijo de tiempo o espacio. Supone que estos sucesos ocurren con una frecuencia media conocida e independientemente del tiempo transcurrido desde el último suceso. Para entender la distribución de Poisson, primero es útil conocer la diferencia entre distribuciones discretas y continuas.
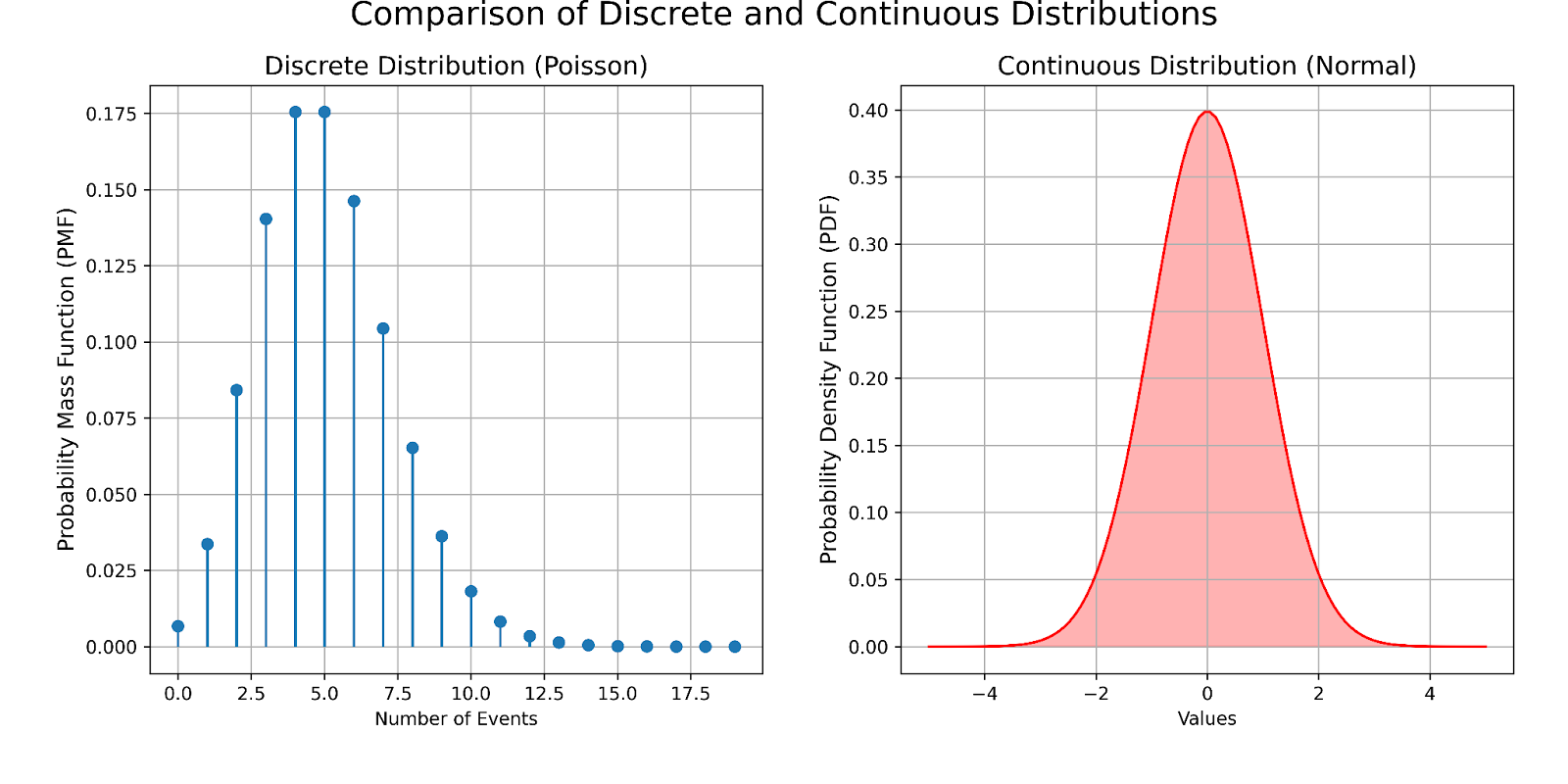
Distribución de Poisson frente a una distribución continua. Imagen del autor
Distribuciones discretas
- Naturaleza: Las distribuciones discretas describen fenómenos en los que los resultados pueden contarse en números enteros. Se caracterizan por funciones de masa de probabilidad (FMP) que asignan una probabilidad a cada posible resultado discreto.
- Visualización: En el panel izquierdo, se muestra la distribución de Poisson, en la que cada punto representa la probabilidad de que se produzca un número determinado de sucesos en un intervalo fijo. Esta distribución es ideal para modelizar datos de recuento, como el número de correos electrónicos recibidos por hora. También puedes observar que no hay valores negativos en el panel de la distribución de Poisson. Esto se debe a que las distribuciones de Poisson, por definición, no pueden tener valores negativos.
Algunos ejemplos de distribuciones discretas de probabilidad son las distribuciones Bernoulli y binomial.
Distribuciones continuas
- Naturaleza: Las distribuciones continuas se utilizan para datos que pueden tomar cualquier valor dentro de un intervalo, incluidos los decimales. Utilizan funciones de densidad de probabilidad (FDP) para describir las probabilidades de los resultados dentro de un intervalo determinado.
- Visualización: El panel derecho ilustra la distribución normal. La curva suave indica la densidad de valores alrededor de la media, y el área bajo la curva entre dos puntos cualesquiera da la probabilidad de caer dentro de ese intervalo. Este tipo de distribución es útil para medir magnitudes como la temperatura o el peso.
La distribución normal, o gaussiana, es un buen ejemplo de distribución continua.
Propiedades de las distribuciones de Poisson
Veamos algunas características importantes de la distribución de Poisson.
Eventos en un intervalo fijo
Una característica clave de la distribución de Poisson es su capacidad para modelizar sucesos en un intervalo fijo. Este intervalo puede ser temporal (por ejemplo, número de clientes que llegan por hora) o espacial (por ejemplo, número de defectos por metro cuadrado de tejido). El modelo supone:
- Los acontecimientos se producen de forma independiente.
- La tasa media de aparición (λ) permanece constante a lo largo del intervalo.
- Dos acontecimientos no pueden ocurrir exactamente en el mismo instante.
Media y varianza
Una de las propiedades más distintivas de la distribución de Poisson es que su media (valor esperado) es igual a su varianza. Ambos están representados por el parámetro λ (lambda), que denota el número medio de sucesos en el intervalo. Esta propiedad es única y ayuda a identificar si un conjunto de datos sigue una distribución de Poisson. Matemáticamente, esto puede representarse en la siguiente ecuación:
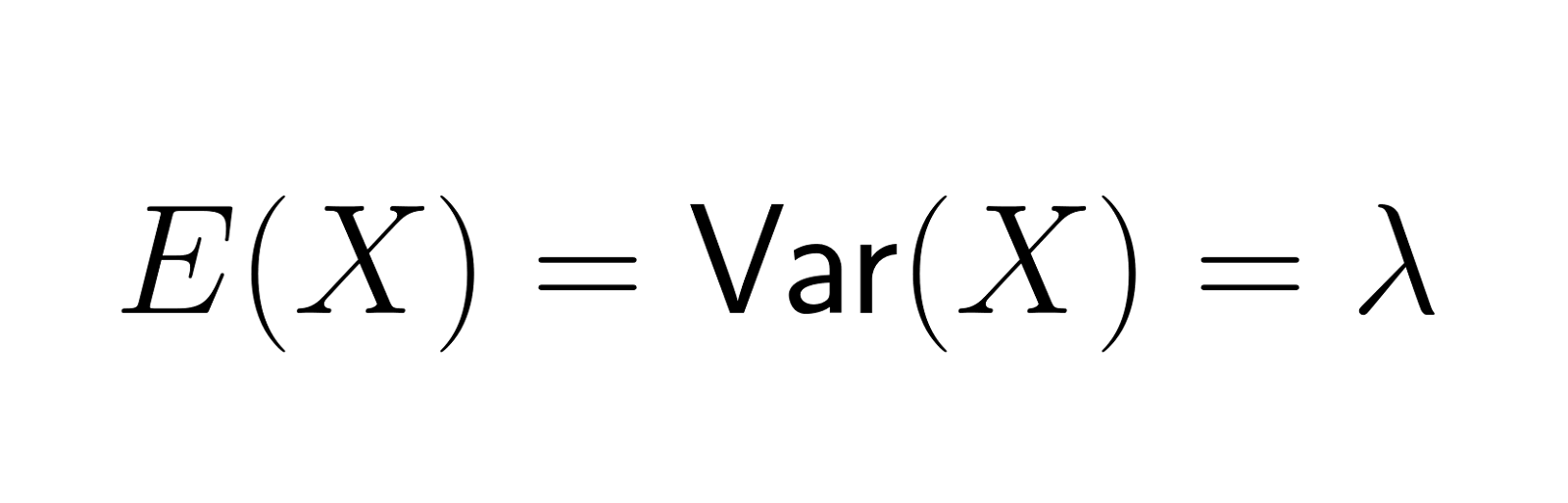
Esta igualdad implica que, a medida que aumenta el número esperado de sucesos, también lo hace la variabilidad en el número real de sucesos.
Asimetría y forma
La forma de la distribución de Poisson varía en función del valor de λ. Esta ilustración visual muestra cómo λ afecta a la asimetría y simetría de la distribución:
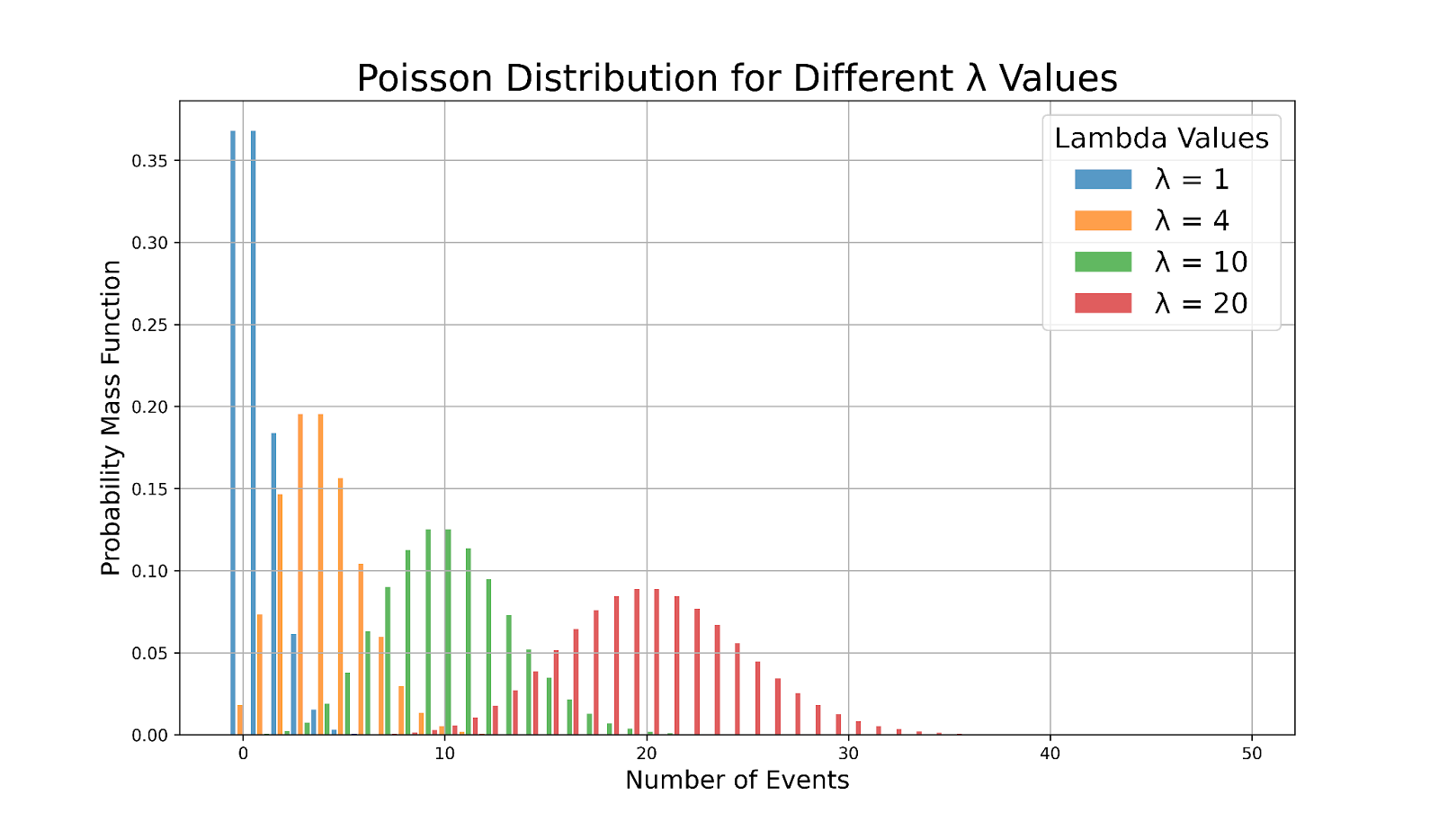
Distribuciones de Poisson con distintos valores de lambda. Imagen del autor
- Para valores pequeños de λ (λ < 10), la distribución es notablemente sesgada a la derecha. Esto significa que hay más sucesos con menos sucesos y menos sucesos con un mayor número de sucesos.
- A medida que aumenta λ (λ > 10), la distribución se vuelve más simétrica y empieza a parecerse a una distribución normal. Esta simetría indica que los datos están distribuidos más uniformemente en torno a la media.
Esta forma cambiante afecta al modo en que interpretamos las probabilidades y hacemos inferencias a partir de datos distribuidos en Poisson. Por ejemplo, una distribución simétrica simplifica muchos tipos de análisis, como las pruebas de hipótesis y la estimación de intervalos de confianza, porque la distribución de los datos es más predecible y equilibrada.
Fórmula de la distribución de Poisson
Echa un vistazo a la fórmula de la distribución de Poisson.
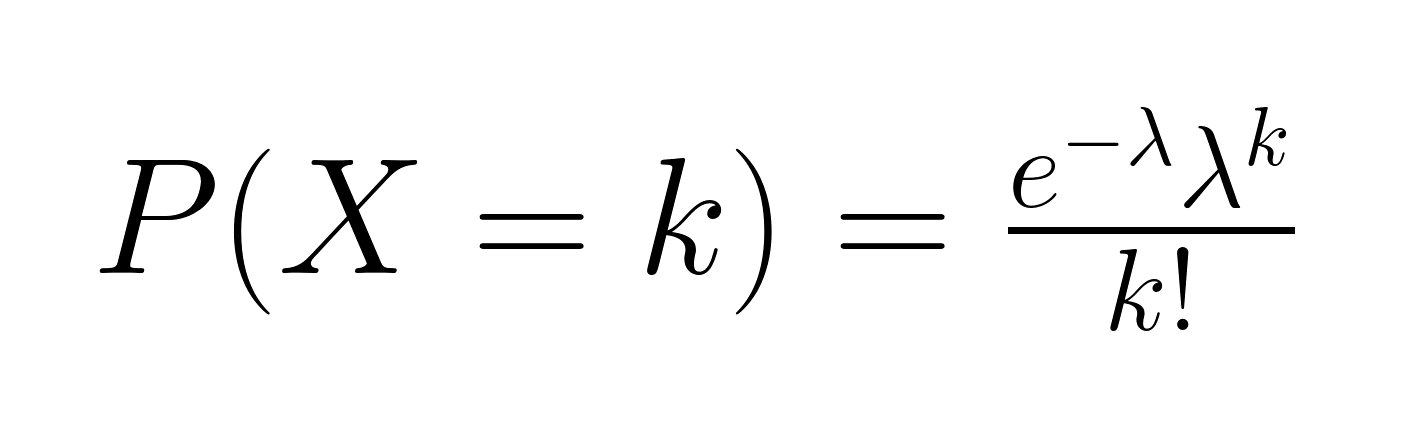
-
El lado izquierdo (LHS) de la fórmula de la distribución de Poisson, P(X = k), representa la probabilidad de que se produzcan exactamente k sucesos en un intervalo fijo. Aquí, X es el número de sucesos, y k es el número concreto que nos interesa. En otras palabras, el LHS nos dice qué probabilidad estamos calculando.
-
El numerador del lado derecho (RHS),e-λλk tiene dos partes. λk muestra la probabilidad de que se produzcan k sucesos basándose en la tasa media λ. La e-λ tiene en cuenta la aleatoriedad de los sucesos, garantizando que la probabilidad disminuye a medida que el número de sucesos se desvía de la tasa esperada.
-
El denominador del lado derecho (RHS), ¡k! ajusta de cuántas maneras pueden ocurrir los sucesosx. La notación factorial calcula el número de disposiciones posibles, asegurándose de que la probabilidad refleja el hecho de que el orden de los acontecimientos no importa.
Si realmente quieres adquirir confianza en el uso de Python para el aprendizaje automático, empieza nuestra carrera de Científico de Aprendizaje Automático con Python, que te permite practicar técnicas avanzadas con conjuntos de datos reales.
Conviértete en un Científico ML
Cómo se utiliza la Distribución de Poisson
Veamos algunos usos reales de la distribución de Poisson. Si te interesa la planificación de la capacidad y la optimización del rendimiento, nuestro curso Modelos de Mezcla en R cubre las aplicaciones avanzadas de las distribuciones de probabilidad, incluidas las mezclas de Poisson.
Teoría de colas
En la teoría de colas, las distribuciones de Poisson modelan las llegadas de clientes a los puntos de servicio. Por ejemplo, un banco podría utilizar esta distribución para predecir cuántos clientes llegarán en una hora determinada, lo que ayudaría a optimizar los niveles de personal y reducir los tiempos de espera.
Epidemiología y acontecimientos raros
Los epidemiólogos emplean con frecuencia distribuciones de Poisson para modelizar la aparición de enfermedades raras. Esta aplicación ayuda a estimar el número esperado de casos en una población, o a detectar brotes inusuales comparando los casos observados con la distribución de Poisson esperada. Si te interesa la epidemiología, puedes escuchar nuestro episodio del podcast Ciencia de datos, epidemiología y salud pública con Maëlle Salmon.
Modelización del tráfico y de la red
Los ingenieros de tráfico y los analistas de redes utilizan las distribuciones de Poisson para modelar el número de vehículos que pasan por un puesto de control, las llegadas de paquetes de datos a un servidor o las llegadas de llamadas a un centro de atención telefónica.
Funcionamiento, conceptos erróneos y alternativas
Al trabajar con distribuciones de Poisson, es esencial tener en cuenta los factores relacionados con el rendimiento, los errores más comunes y los modelos alternativos para garantizar resultados precisos. Merece la pena explorar varias zonas:
Retos de rendimiento
Varios factores influyen en la eficacia del modelado de la distribución de Poisson, sobre todo cuando se tratan casos extremos:
- Tasas de eventos bajos: Cuando se trata de tasas de sucesos muy bajas (λ pequeñas), surgen dificultades debido a la gran variabilidad de los resultados. Las estrategias para gestionar esto incluyen utilizar periodos de observación más largos para aumentar el recuento esperado, emplear métodos bayesianos para incorporar el conocimiento previo, o considerar modelos cero-inflados para el exceso de ceros.
- Aproximaciones con distribución normal: Para valores de λ mayores (normalmente por encima de 30), la distribución de Poisson puede aproximarse utilizando una distribución normal, lo que simplifica los cálculos pero requiere una aplicación cuidadosa.
Aclarar conceptos erróneos
Entender mal los elementos clave puede conducir a modelos defectuosos:
- Intervalos fijos: Un error común es creer que el intervalo en un proceso de Poisson puede variar. En realidad, el intervalo debe ser fijo y bien definido. La variación de los intervalos puede dar lugar a una modelización incorrecta y a predicciones inexactas.
- Confusión con la distribución binomial: Aunque la distribución de Poisson puede derivarse como límite de la distribución binomial en determinadas condiciones, son distintas. La distribución de Poisson se utiliza para contar sucesos raros en un intervalo fijo de tiempo o espacio, mientras que la binomial es para un número fijo de ensayos independientes con dos resultados posibles.
Considerando distribuciones alternativas
En algunos casos, las distribuciones alternativas pueden ofrecer mejores resultados:
- Distribución binomial negativa: La distribución binomial negativa es una alternativa para los datos de recuento sobredispersos, en los que la varianza supera a la media. Es más flexible que la distribución de Poisson y puede modelizar datos con mayor variabilidad.
- Distribución exponencial: Mientras que la distribución de Poisson modela el número de sucesos en un intervalo fijo, la distribución exponencial modela el tiempo entre sucesos en un proceso de Poisson. Es continua en lugar de discreta y es crucial en el análisis de supervivencia y la ingeniería de fiabilidad.
Reflexiones finales sobre la distribución de Poisson
Comprender las distribuciones de Poisson mejora notablemente el análisis estadístico y la interpretación de los datos, sobre todo cuando se analizan sucesos poco frecuentes o datos de recuento. Al comprender sus propiedades, aplicaciones y limitaciones, los profesionales de los datos pueden mejorar sus procesos de toma de decisiones y crear modelos más precisos.
A medida que avances en la ciencia de datos, considera la posibilidad de ampliar tus conocimientos de los conceptos estadísticos y sus aplicaciones prácticas. Para los que trabajan con R, el curso Introducción a la Estadística en R y el itinerario de habilidades Fundamentos de Estadística con R ofrecen una visión completa de los principios estadísticos clave, incluida la experiencia práctica con distribuciones como la de Poisson. Para quienes prefieran trabajar con Python, nuestro curso Introducción a la Estadística en Python ofrece experiencia práctica en la aplicación de conceptos estadísticos, incluyendo optimizaciones de rendimiento. Si sigues desarrollando tus habilidades estadísticas, estarás preparado para enfrentarte a retos de datos complejos y extraer ideas significativas en tu trabajo.
Conviértete en un Científico ML
Como profesional experto en Ciencia de Datos, Aprendizaje Automático e IA Generativa, Vinod se dedica a compartir conocimientos y a capacitar a los aspirantes a científicos de datos para que tengan éxito en este dinámico campo.
Preguntas frecuentes sobre la distribución de Poisson
¿Qué es una distribución de Poisson?
La distribución de Poisson es un modelo estadístico que predice cuántas veces puede ocurrir un acontecimiento poco frecuente en un periodo o área concretos. Es especialmente útil cuando se trata de sucesos que ocurren aleatoriamente, pero a un ritmo medio predecible. Esta distribución nos ayuda a comprender patrones en sucesos aparentemente aleatorios, desde el número de clientes que llegan a una tienda en una hora hasta el recuento de impactos de meteoritos en la superficie de un planeta a lo largo de un siglo.
¿Cuándo debes utilizar una distribución de Poisson?
Debes utilizar una distribución de Poisson cuando modelices escenarios en los que los sucesos ocurren de forma aleatoria e independiente a una tasa constante dentro de un intervalo determinado, como el número de correos electrónicos recibidos en una hora o de llamadas en un centro de atención telefónica durante un turno.
¿En qué se diferencia la distribución de Poisson de la distribución normal?
La distribución de Poisson se utiliza para datos de recuento discretos con un número potencialmente pequeño de sucesos, mientras que la distribución normal suele modelar datos continuos y se convierte en una buena aproximación para Poisson cuando la tasa de sucesos (λ) es grande.
¿Cuál es la relación entre las distribuciones de Poisson y exponencial?
La distribución de Poisson cuenta el número de sucesos en un intervalo fijo, mientras que la distribución exponencial mide el tiempo entre sucesivos sucesos en un proceso de Poisson. Están matemáticamente relacionadas: conocer la tasa de ocurrencias en Poisson ayuda a determinar la escala de la distribución exponencial.
¿Puede utilizarse la distribución de Poisson para modelizar cualquier tipo de datos?
No, la distribución de Poisson es específicamente útil para modelizar el recuento de sucesos discretos que ocurren independientemente dentro de un intervalo o región fijos, y supone una tasa media constante. No es adecuado para datos en los que los acontecimientos se influyen mutuamente o se producen a ritmos no constantes.
¿Qué significa λ en una distribución de Poisson?
En una distribución de Poisson, λ (lambda) representa el número esperado de sucesos en el intervalo. Es tanto la media como la varianza de la distribución.
¿Cómo se crea una distribución de Poisson en Python?
Para crear una distribución de Poisson en Python, utiliza principalmente el módulo random de la biblioteca NumPy. La función np.random.poisson() genera muestras aleatorias a partir de una distribución de Poisson, en la que tú especificas la tasa media de sucesos (lambda) y el número de muestras que deseas. Luego puedes utilizar estas muestras para trazar histogramas, calcular probabilidades o realizar análisis estadísticos. Para cálculos de probabilidad más precisos, el módulo stats de la biblioteca SciPy ofrece funciones como stats.poisson.pmf() para la función de masa de probabilidad y stats.poisson.cdf() para la función de distribución acumulativa.
¿Cómo se crea una distribución de Poisson en R?
Para crear una distribución de Poisson en R, puedes utilizar las funciones incorporadas que forman parte del paquete estadístico base de R. R proporciona funciones para generar números aleatorios, calcular probabilidades y trazar distribuciones de Poisson. Las principales funciones son rpois() para generar números aleatorios, dpois() para la densidad de probabilidad, ppois() para la probabilidad acumulada y qpois() para los cuantiles. Puedes utilizar estas funciones junto con las capacidades de trazado de R para crear y visualizar distribuciones de Poisson.
¿Cómo se relaciona la distribución de Poisson con la regresión de Poisson?
Mientras que la distribución de Poisson describe la probabilidad de que se produzca un número de sucesos en un intervalo fijo, la regresión de Poisson es un método estadístico utilizado para modelizar datos de recuento y comprender cómo influyen las distintas variables en estos recuentos. En la regresión de Poisson, se supone que la variable de respuesta sigue una distribución de Poisson, y el logaritmo de su valor esperado se modela como una combinación lineal de variables predictoras. Esta relación permite a los investigadores analizar cómo afectan diversos factores a la tasa de ocurrencia de los acontecimientos.



