Die Exponentialverteilung verstehen: Ein umfassender Leitfaden

Das Verständnis von Wahrscheinlichkeitsverteilungen ist für die Datenwissenschaft von grundlegender Bedeutung, und ich finde, dass die Exponentialverteilung einige einzigartige Eigenschaften aufweist, die es zu erforschen lohnt. Obwohl sie mathematisch mit der Poisson-Verteilung verwandt ist, modelliert die Exponentialverteilung ausschließlich Zeitintervalle zwischen Ereignissen und nicht die Anzahl der Ereignisse. 

Für diejenigen, die noch nicht mit Wahrscheinlichkeitskonzepten vertraut sind, vermittelt unser Kurs Grundlagen der Wahrscheinlichkeit in Python wichtiges Hintergrundwissen. Die praktischen Anwendungen der Exponentialverteilung erstrecken sich über verschiedene Bereiche, von der Zuverlässigkeitstechnik bis zur Warteschlangentheorie, und machen sie besonders wertvoll in Bereichen wie der Überlebensanalyse, die in Survival Analysis in Python eingehend untersucht wird. In diesem Leitfaden werden die grundlegenden Konzepte, mathematischen Grundlagen und realen Anwendungen der Exponentialverteilung erläutert, damit du sie in deinen Data Science-Projekten effektiv einsetzen kannst.

Was ist die Exponentialverteilung?

Die Exponentialverteilung ist eine kontinuierliche Wahrscheinlichkeitsverteilung, die die Zeit zwischen Ereignissen in einem Prozess modelliert, in dem Ereignisse kontinuierlich und unabhängig voneinander mit einer konstanten durchschnittlichen Rate auftreten. Es ist besonders nützlich für die Analyse von Situationen, die Wartezeiten, Lebenszeiten und Intervalle zwischen Ereignissen beinhalten.

Stell dir vor, du arbeitest in einem geschäftigen Kundenservicecenter. Die Zeit zwischen eingehenden Kundenanrufen folgt oft einer Exponentialverteilung. Ähnlich verhält es sich in der Produktion: Die Zeit, bis eine Maschine ausfällt oder gewartet werden muss, verhält sich häufig exponentiell.

Die wichtigsten Merkmale der Exponentialverteilung

Die Exponentialverteilung hat mehrere einzigartige Eigenschaften, die sie in realen Anwendungen besonders nützlich machen:

Die gedächtnislose Eigenschaft

Dies ist vielleicht das markanteste Merkmal der Exponentialverteilung. Das bedeutet, dass das zukünftige Verhalten des Systems nicht von seiner Vergangenheit abhängt. Wenn eine Glühbirne zum Beispiel schon 1000 Stunden gehalten hat, ist die Wahrscheinlichkeit, dass sie weitere 100 Stunden hält, die gleiche wie bei einer nagelneuen Glühbirne. Diese Eigenschaft ist einzigartig für die Exponentialverteilung unter den kontinuierlichen Verteilungen.

Konstante Hazard Rate

Die Exponentialverteilung sorgt für eine konstante Ausfallrate im Laufe der Zeit. Das bedeutet, dass die Wahrscheinlichkeit, dass ein Ereignis im nächsten kleinen Zeitintervall eintritt, gleich bleibt, unabhängig davon, wie viel Zeit vergangen ist.

Die Beziehung zwischen der Exponential- und der Poisson-Verteilung ist grundlegend für die Wahrscheinlichkeitstheorie. Während die Poisson-Verteilung die Anzahl der Ereignisse modelliert, die in einem bestimmten Zeitintervall auftreten, modelliert die Exponentialverteilung die Zeit zwischen diesen Ereignissen. Das sind zwei Seiten derselben Medaille: Wenn Ereignisse nach einem Poisson-Prozess mit der Rate λ auftreten, dann folgt die Wartezeit zwischen den Ereignissen einer Exponentialverteilung mit dem Parameter λ.

Mathematische Formulierung

Die Exponentialverteilung wird durch einen einzigen Parameter λ (lambda) definiert, der den Ratenparameter darstellt. Schauen wir uns die wichtigsten mathematischen Komponenten an:

Wahrscheinlichkeitsdichtefunktion (PDF)

Die PDF hilft uns, die Wahrscheinlichkeit zu berechnen, dass ein Ereignis innerhalb eines bestimmten Intervalls eintritt. Die PDF für die Exponentialverteilung lautet wie folgt:   

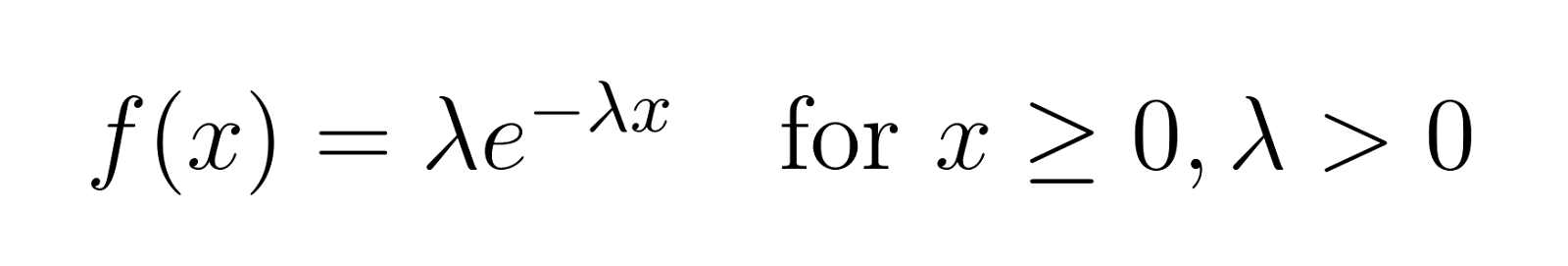
   wo:

• x ist die Zufallsvariable (typischerweise die Zeit)
• λ ist der Ratenparameter (λ > 0)
• e ist die Eulersche Zahl (ungefähr 2,71828)

Kumulative Verteilungsfunktion (CDF)

Die CDF ist besonders nützlich, wenn wir die Wahrscheinlichkeit ermitteln wollen, dass ein Ereignis vor einer bestimmten Zeit eintritt. Sie gibt uns die Wahrscheinlichkeit, dass die Wartezeit kleiner oder gleich einem bestimmten Wert ist. Hier ist die CDF für die Exponentialverteilung:

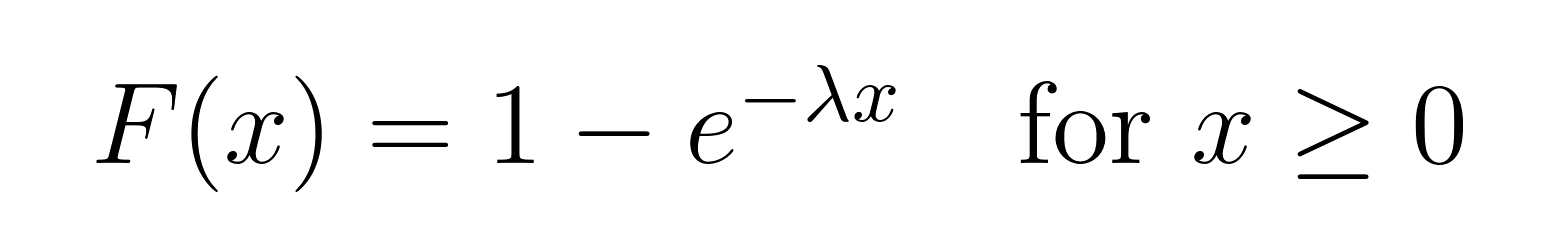
Anwendungen der Exponentialverteilung

Die Exponentialverteilung spielt in verschiedenen Bereichen eine wichtige Rolle und hilft uns, zeitabhängige Prozesse zu modellieren und zu verstehen. Sehen wir uns einige der wichtigsten Anwendungen an. 

Zuverlässigkeitstechnik

Die Zuverlässigkeitstechnik stützt sich stark auf die Exponentialverteilung, um die Lebensdauer von Komponenten und Systemen zu modellieren. Das ist besonders nützlich, weil die Verteilung eine "gedächtnislose" Eigenschaft hat - die zukünftige Lebensdauer einer Komponente hängt nur von der Gegenwart ab, nicht davon, wie lange sie bereits in Betrieb ist.

Elektronische Bauteile weisen zum Beispiel typischerweise exponentiell verteilte Ausfallzeiten auf, was die einzigartige Eigenschaft dieser Verteilung zeigt, dass sie kein Gedächtnis hat. Das bedeutet, dass ein neuer Mikroprozessor die gleiche Wahrscheinlichkeit hat, in der nächsten Stunde auszufallen, wie ein Mikroprozessor, der schon einen Monat lang läuft (vorausgesetzt, es gibt keine Abnutzungseffekte). Hersteller von Server-Hardware nutzen diese Verteilung häufig in ihren Zuverlässigkeitsanalysen, um die mittlere Betriebsdauer zwischen Ausfällen (MTBF) zu berechnen, optimale Wartungspläne zu bestimmen und Garantiekosten und Ersatzbedarf vorherzusagen. Diese Informationen sind sowohl für die Produktentwicklung als auch für die Geschäftsplanung wertvoll.

Warteschlangentheorie

In der Warteschlangentheorie ist die Exponentialverteilung von grundlegender Bedeutung für die Modellierung der Zeit zwischen Ankünften oder Servicezeiten in vielen Systemen. Diese Anwendung ist besonders nützlich bei:

1. Kundendienstzentren:

• Modellierung der Zeit zwischen eingehenden Anrufen
• Vorhersage von Spitzenlastzeiten
• Optimierung der Personaleinsatzplanung

2. Telekommunikation:

• Analysieren von Netzwerkverkehrsmustern
• Modellierung von Paketankunftszeiten in Datennetzen
• Planung der Netzwerkkapazität

3. Gesundheitssysteme:

• Modellierung der Ankunftszeiten von Patienten in Notaufnahmen
• Schätzung der Wartezeiten für Dienstleistungen
• Planung der Ressourcenzuweisung

Die Exponentialverteilung funktioniert in diesem Zusammenhang gut, weil viele Ankunftsprozesse als speicherlose Ereignisse mit einer konstanten Durchschnittsrate approximiert werden können.

Berechnung von Wahrscheinlichkeiten mit der Exponentialverteilung

Bei der Arbeit mit der Exponentialverteilung gibt es zwei Hauptansätze zur Berechnung von Wahrscheinlichkeiten: Die PDF ist besonders nützlich, wenn wir die Wahrscheinlichkeit eines Ereignisses innerhalb eines bestimmten Intervalls oder Bereichs ermitteln müssen, während die CDF uns hilft, die Wahrscheinlichkeit eines Ereignisses vor einem bestimmten Zeitpunkt zu bestimmen. Lass uns beide Ansätze anhand eines praktischen Helpdesk-Szenarios untersuchen.

Mit Hilfe der Wahrscheinlichkeitsdichtefunktion

Wir haben erwähnt, dass die PDF uns hilft, die Wahrscheinlichkeit zu berechnen, dass ein Ereignis innerhalb eines Intervalls eintritt. Bei kontinuierlichen Verteilungen wie der Exponentialverteilung müssen wir die PDF über das Intervall integrieren, das uns interessiert.

Lass uns ein praktisches Beispiel durchspielen: Stell dir vor, wir analysieren Kundendienstanrufe bei einem Helpdesk, bei dem die Anrufe einer Exponentialverteilung mit einer durchschnittlichen Rate von 3 Anrufen pro Stunde (λ = 3) folgen.

Um die Wahrscheinlichkeit zu ermitteln, dass du zwischen 10 und 20 Minuten auf den nächsten Anruf wartest, müssten wir:

1. Rechne die Zeit in Stunden um: (10 Minuten = 1/6 Stunde, 20 Minuten = 1/3 Stunde)
2. Verwende die Formel: P(1/6 < X < 1/3) = ∫[1/6 bis 1/3] 3e^(-3x)dx
3. Auswerten: = -e^{(-3x)|[1/6 bis 1/3]}
4. Berechne: = [e^(-0,5) - e^(-1)] ≈ 0,2325 oder etwa 23,25%

Verwendung der kumulativen Verteilungsfunktion

Wir haben gesagt, dass die CDF nützlich ist, wenn wir die Wahrscheinlichkeit eines Ereignisses vor einem bestimmten Zeitpunkt ermitteln wollen. Nehmen wir unser Helpdesk-Beispiel: Wie hoch ist die Wahrscheinlichkeit, dass wir innerhalb der ersten 15 Minuten einen Anruf erhalten?

Nehmen wir unser Helpdesk-Beispiel: Wie hoch ist die Wahrscheinlichkeit, dass wir innerhalb der ersten 15 Minuten einen Anruf erhalten?

1. Rechne 15 Minuten in Stunden um: (15 Minuten = 1/4 Stunde)
2. Verwende die CDF-Formel: F(1/4) = 1 - e^(-3*1/4)
3. Berechne: = 1 - e^(-0,75) ≈ 0,5276 oder etwa 52,76%

Das bedeutet, dass die Chance, innerhalb der ersten 15 Minuten einen Anruf zu erhalten, bei etwa 53 % liegt. Beachte, dass die CDF diese "bis zu"-Wahrscheinlichkeitsberechnungen unkomplizierter macht als die Verwendung der PDF.

Visualisierung der Exponentialverteilung

Schauen wir uns zunächst die Exponentialverteilung selbst an und vergleichen sie dann mit anderen Verteilungen.

Grafische Darstellung

Hier ist eine Reihe von Diagrammen, die ich in Python erstellt habe:

Lass uns herausfinden, wie die mathematischen Formeln in visuelle Muster übersetzt werden. Die Visualisierung zeigt drei verschiedene Ratenparameter (0,5, 1,0 und 2,0), um zu verdeutlichen, wie λ die Verteilung beeinflusst:

Schau dir das PDF an (obere Grafik):

• Bei λ = 2,0 (grüne Linie) sehen wir den steilsten anfänglichen Rückgang, beginnend bei f(0) = 2,0. Dies zeigt, dass frühe Ereignisse viel wahrscheinlicher sind
• Wenn λ = 1,0 (orangefarbene Linie), erhalten wir die Standard-Exponentialverteilung mit einem moderateren Abklingen
• Bei λ = 0,5 (rote Linie) fällt die Kurve allmählicher ab, was zeigt, dass längere Wartezeiten häufiger vorkommen

Die CDF (unteres Diagramm) erzählt eine ergänzende Geschichte:

• Die höhere Rate (λ = 2,0) ergibt den steilsten Anstieg, was zeigt, dass die kumulierte Wahrscheinlichkeit schnell ansteigt
• Die niedrigere Rate (λ = 0,5) zeigt eine allmählichere Akkumulation der Wahrscheinlichkeit
• Alle Kurven nähern sich schließlich der Zahl 1, was zeigt, dass sich die Wahrscheinlichkeit, dass das Ereignis eintritt, mit zunehmender Zeit der Gewissheit nähert

Dieses Verhalten macht die Exponentialverteilung besonders nützlich für die Modellierung realer Phänomene wie Wartezeiten, Lebensdauer von Geräten und Zeit zwischen Ereignissen in einem Poisson-Prozess.

Vergleich mit anderen Verteilungen

Die einzigartigen Eigenschaften der Exponentialverteilung werden deutlicher, wenn man sie mit anderen gängigen Wahrscheinlichkeitsverteilungen vergleicht. Lass uns diese Vergleiche mit Hilfe unserer Visualisierung untersuchen:

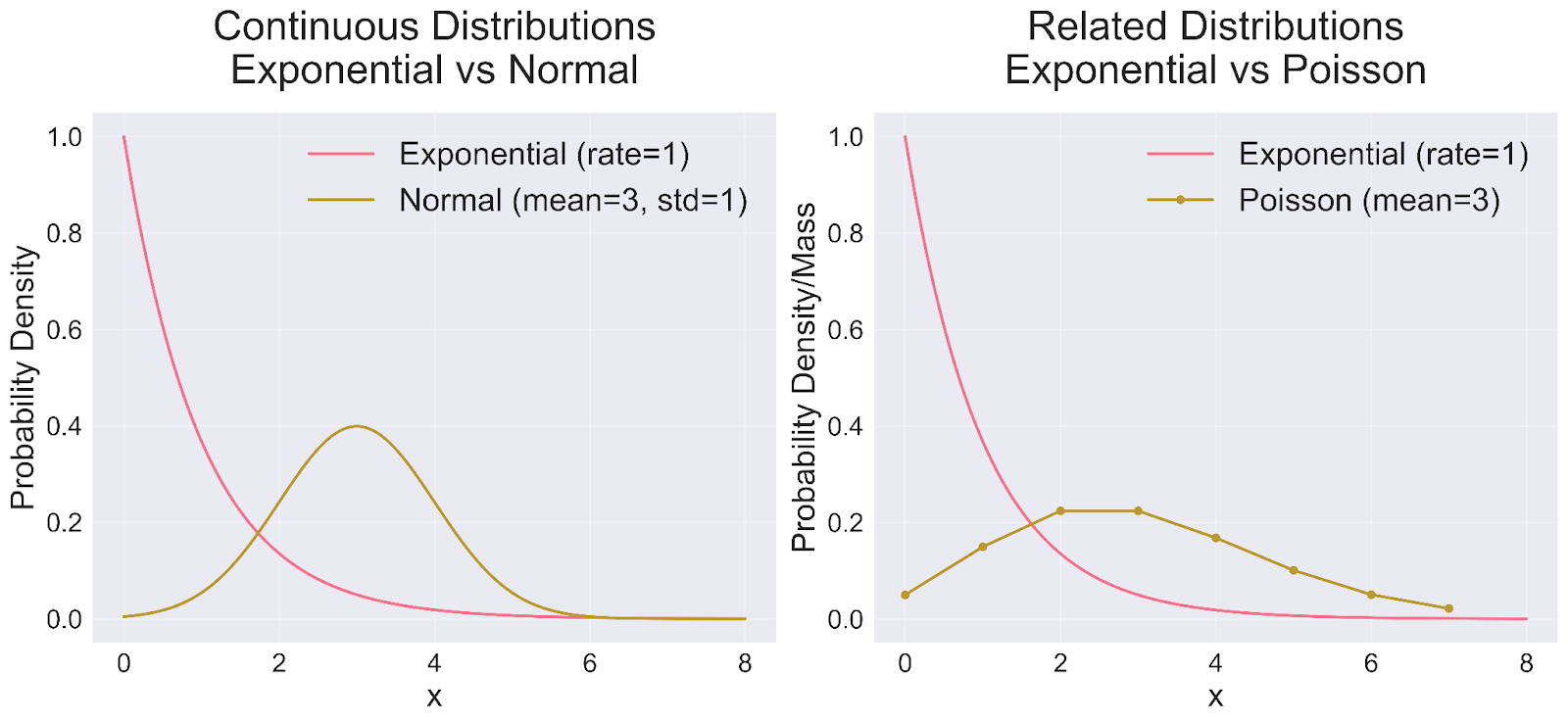
Beim Vergleich mit der Normalverteilung (linkes Feld) werden einige wichtige Unterschiede deutlich. Die Exponentialverteilung weist eine ausgeprägte Rechtsschiefe auf und erreicht ihren Spitzenwert sofort, bevor sie kontinuierlich abnimmt. Dies steht in starkem Kontrast zu der bekannten symmetrischen, glockenförmigen Kurve der Normalverteilung, die um ihren Mittelwert zentriert ist. Obwohl beide als kontinuierliche Verteilungen gelten, dienen sie unterschiedlichen Modellierungszwecken: Die Exponentialverteilung eignet sich hervorragend zur Modellierung von Wartezeiten und Intervallen, während die Normalverteilung typischerweise für Messungen und Durchschnittswerte verwendet wird.

Die Beziehung zur Poisson-Verteilung (rechtes Feld) zeigt eine weitere faszinierende Dimension der Wahrscheinlichkeitstheorie. Während die Exponentialverteilung die Zeit zwischen den Ereignissen misst, konzentriert sich die Poisson-Verteilung darauf, die Anzahl der Ereignisse innerhalb eines festen Intervalls zu zählen. Diese Verteilungen sind zwei Seiten derselben Medaille: Bei einem Poisson-Prozess folgen die Wartezeiten natürlich einer Exponentialverteilung. Ein weiterer bemerkenswerter Unterschied liegt in ihrer Kontinuität - die Exponentialverteilung kann jeden positiven reellen Wert annehmen, während die Poisson-Verteilung ausschließlich mit diskreten, nichtnegativen ganzen Zahlen arbeitet.

Diese vergleichenden Erkenntnisse machen deutlich, warum die Exponentialverteilung in bestimmten Modellierungsszenarien besser abschneidet. Sie ist von unschätzbarem Wert, wenn es darum geht, Zeitintervalle zwischen zufälligen Ereignissen zu analysieren, und bietet Möglichkeiten, die über die Ereigniszählung der Poisson-Verteilung hinausgehen. Die Verteilung eignet sich besonders gut für Szenarien, die eine unmittelbare Einschätzung der Eintrittswahrscheinlichkeit erfordern, im Gegensatz zur Normalverteilung, die eine zentrale Tendenz hat. Das Besondere an ihr ist vielleicht, dass sie sich durch ihre einzigartige gedächtnislose Eigenschaft sowohl von der Normal- als auch von der Poisson-Verteilung unterscheidet, was sie zur optimalen Wahl für Prozesse macht, bei denen vergangene Ereignisse keinen Einfluss auf zukünftige Wahrscheinlichkeiten haben.

Häufige Missverständnisse und Fallstricke

Bei der Arbeit mit der Exponentialverteilung gibt es einige häufige Missverständnisse, die zu falschen Analysen führen können. Das Wissen um diese potenziellen Fallstricke trägt dazu bei, dass die Verteilung in realen Szenarien korrekt angewendet wird.

Fehlinterpretation der gedächtnislosen Eigenschaft

Die gedächtnislose Eigenschaft sorgt oft für Verwirrung, weil sie unserer Alltagserfahrung zu widersprechen scheint. Hier sind häufige Missverständnisse und ihre Korrekturen:

Ein häufiges Missverständnis ist die Annahme, dass die gedächtnislose Eigenschaft bedeutet, dass vergangene Ereignisse keinen Wert für Vorhersagen haben. In Wirklichkeit bedeutet das, dass die Wahrscheinlichkeit, eine weitere Zeitspanne zu warten, gleich bleibt, unabhängig davon, wie lange du bereits gewartet hast. Zum Beispiel:

• Falsche Interpretation: "Wenn eine Glühbirne einer Exponentialverteilung folgt und seit 5 Jahren nicht ausgefallen ist, muss sie bald ausfallen."
• Richtige Interpretation: "Wenn eine Glühbirne einer Exponentialverteilung folgt und seit 5 Jahren nicht ausgefallen ist, ist die Wahrscheinlichkeit, dass sie ein weiteres Jahr hält, die gleiche wie bei einer neuen Glühbirne, die ein Jahr hält."

Ein weiterer Irrtum ist die Annahme, dass alle Zuverlässigkeitsszenarien die Eigenschaft der Gedächtnislosigkeit aufweisen. In der Realität zeigen viele Systeme Alterungseffekte oder Abnutzungsmuster, die nicht einem exponentiellen Verhalten folgen. Bei mechanischen Bauteilen zum Beispiel steigt die Ausfallrate mit der Zeit.

Falsche Verwendung von Parametern

Bei der Auswahl und Anwendung des Tarifparameters treten häufig mehrere Fehler auf:

1. Rate vs. mittlere Verwirrung:

   • Ein häufiger Fehler ist die Verwendung des Mittelwerts als Parameter für die Rate (λ)

   • Erinnere dich: Der Mittelwert (Erwartungswert) ist eigentlich 1/λ

   • Wenn Ereignisse zum Beispiel im Durchschnitt alle 2 Stunden auftreten, ist λ = 1/2, nicht 2

2. Die Einheiten passen nicht zusammen:

   • Der Ratenparameter muss mit den Zeiteinheiten in deinen Daten übereinstimmen

   • Wenn du die Zeit in Stunden misst, aber λ in Tagen^(-1) angibst, werden deine Wahrscheinlichkeiten falsch sein

   • Konvertiere immer in konsistente Einheiten, bevor du die Verteilung anwendest.

3. Übermäßiges Auftragen:

   • Die Gewissheit, dass Ereignisse unabhängig voneinander auftreten

   • Dass die Rate im Laufe der Zeit konstant bleibt

   • Und dass der Prozess keine Memory-Effekte hat 

Um diese Fehler zu vermeiden, solltest du deine Einheiten immer klar definieren und konsequent umrechnen, überprüfen, ob die Annahmen der Exponentialverteilung zu deinem Szenario passen, deine Daten auf exponentielles Verhalten testen, bevor du die Verteilung anwendest, und deine Parameterwahl und deren Begründung dokumentieren.

Fazit

Die elegante Einfachheit der Exponentialverteilung und ihre leistungsstarken Anwendungen machen sie zu einem unverzichtbaren Werkzeug im Werkzeugkasten eines Datenwissenschaftlers. Ihre einzigartige speicherlose Eigenschaft und ihre Beziehung zu anderen Verteilungen, insbesondere der Gauß-Verteilung, unterstreichen ihre besondere Stellung in der Wahrscheinlichkeitstheorie.

Auch wenn dieser Leitfaden die wichtigsten Aspekte behandelt hat, gibt es bei speziellen Anwendungen immer noch mehr zu entdecken. Für diejenigen, die sich für die praktische Umsetzung interessieren, bietet unser Kurs Statistische Simulation in Python praktische Erfahrungen mit diesen Konzepten. Wenn du verstehst, wie die Exponentialverteilung mit anderen Wahrscheinlichkeitsverteilungen zusammenhängt, wie in Multivariate Wahrscheinlichkeitsverteilungen in R beschrieben, kannst du ihre Rolle in der statistischen Modellierung besser verstehen. Egal, ob du Überlebensdaten analysierst, die Zuverlässigkeit von Systemen modellierst oder das Verhalten von Warteschlangen untersuchst, die Beherrschung der Exponentialverteilung eröffnet dir neue Möglichkeiten der Datenanalyse und statistischen Modellierung.