Entendendo a distribuição exponencial: Um guia abrangente

Entender as distribuições de probabilidade é fundamental para a ciência de dados e, entre elas, acho que a distribuição exponencial se destaca como uma distribuição com alguns recursos exclusivos que vale a pena explorar. Embora compartilhe conexões matemáticas com a distribuição de Poisson, a distribuição exponencial modela exclusivamente intervalos de tempo entre eventos em vez de contagens de eventos. 

Para os iniciantes em conceitos de probabilidade, nosso curso Foundations of Probability in Python fornece o conhecimento básico essencial. As aplicações práticas da distribuição exponencial se estendem por vários domínios, desde a engenharia de confiabilidade até a teoria das filas, tornando-a particularmente valiosa em campos como a análise de sobrevivência, que é explorada em profundidade em Survival Analysis in Python. Este guia explorará os conceitos fundamentais, os fundamentos matemáticos e as aplicações no mundo real da distribuição exponencial, equipando você com o conhecimento necessário para aplicá-la efetivamente em seus projetos de ciência de dados.

O que é a distribuição exponencial?

A distribuição exponencial é uma distribuição de probabilidade contínua que modela o tempo entre eventos em um processo em que os eventos ocorrem de forma contínua e independente a uma taxa média constante. É particularmente útil para analisar situações que envolvem tempos de espera, tempos de vida e intervalos entre eventos.

Imagine que você está trabalhando em uma central de atendimento ao cliente movimentada. O tempo entre as chamadas recebidas de clientes geralmente segue uma distribuição exponencial. Da mesma forma, na produção, o tempo até que uma máquina falhe ou precise de manutenção frequentemente apresenta um comportamento exponencial.

Principais características da distribuição exponencial

A distribuição exponencial tem várias propriedades exclusivas que a tornam particularmente útil em aplicações do mundo real:

A propriedade sem memória

Essa talvez seja a característica mais marcante da distribuição exponencial. Isso significa que o comportamento futuro do sistema não depende de seu histórico anterior. Por exemplo, se uma lâmpada já durou 1.000 horas, a probabilidade de ela durar mais 100 horas é a mesma que se ela fosse nova. Essa propriedade é exclusiva da distribuição exponencial entre as distribuições contínuas.

Taxa de risco constante

A distribuição exponencial mantém uma taxa de falha constante ao longo do tempo. Isso significa que a probabilidade de um evento ocorrer no próximo pequeno intervalo de tempo permanece a mesma, independentemente do tempo decorrido.

A relação entre as distribuições exponencial e de Poisson é fundamental na teoria da probabilidade. Enquanto a distribuição de Poisson modela o número de eventos que ocorrem em um intervalo de tempo fixo, a distribuição exponencial modela o tempo entre esses eventos. São dois lados da mesma moeda: se os eventos ocorrem de acordo com um processo de Poisson com taxa λ, então o tempo de espera entre os eventos segue uma distribuição exponencial com parâmetro λ.

Formulação matemática

A distribuição exponencial é definida por um único parâmetro λ (lambda), que representa o parâmetro de taxa. Vamos dar uma olhada em seus principais componentes matemáticos:

Função de densidade de probabilidade (PDF)

O PDF nos ajuda a calcular a probabilidade de ocorrência de um evento em um intervalo específico. O PDF da distribuição exponencial é o seguinte:   

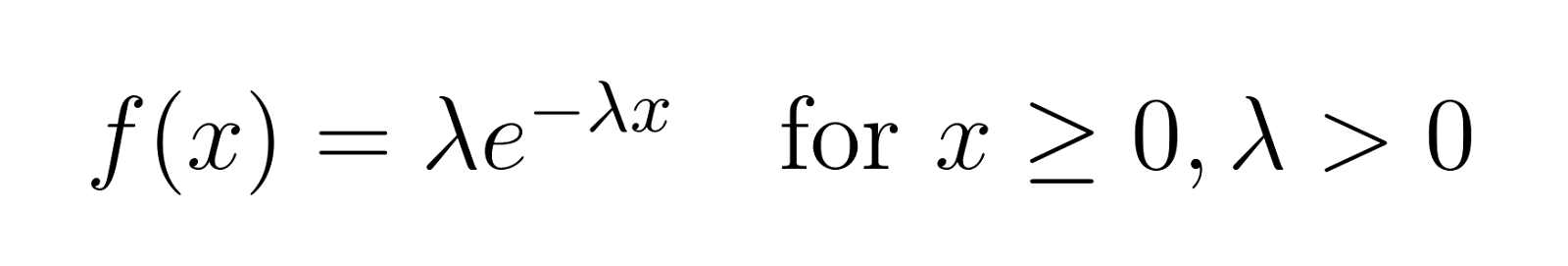
   onde:

• x é a variável aleatória (normalmente representando o tempo)
• λ é o parâmetro de taxa (λ > 0)
• e é o número de Euler (aproximadamente 2,71828)

Função de distribuição cumulativa (CDF)

O CDF é particularmente útil quando você deseja encontrar a probabilidade de um evento ocorrer antes de um determinado momento. Ele nos dá a probabilidade de que o tempo de espera seja menor ou igual a um valor específico. Aqui está o CDF da distribuição exponencial:

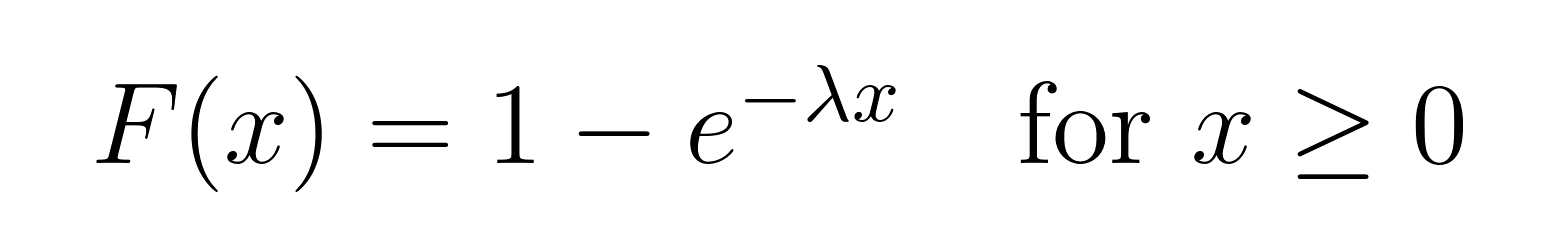
Aplicações da distribuição exponencial

A distribuição exponencial desempenha um papel fundamental em vários campos, ajudando-nos a modelar e entender os processos dependentes do tempo. Vamos explorar alguns de seus principais aplicativos. 

Engenharia de confiabilidade

A engenharia de confiabilidade se baseia muito na distribuição exponencial para modelar a vida útil de componentes e sistemas. Isso é particularmente útil devido à propriedade "sem memória" da distribuição - a vida útil futura de um componente depende apenas do presente, não de quanto tempo ele já está em operação.

Por exemplo, os componentes eletrônicos normalmente apresentam tempos de falha distribuídos exponencialmente, demonstrando a propriedade exclusiva de ausência de memória dessa distribuição. Isso significa que um microprocessador novo tem a mesma probabilidade de falhar na próxima hora do que um que esteja funcionando há um mês (supondo que não haja efeitos de desgaste). Os fabricantes de hardware de servidor usam amplamente essa distribuição em suas análises de confiabilidade para calcular o tempo médio entre falhas (MTBF), determinar cronogramas de manutenção ideais e prever custos de garantia e necessidades de substituição. Essas informações são valiosas tanto para o desenvolvimento de produtos quanto para o planejamento de negócios.

Teoria das filas

Na teoria das filas, a distribuição exponencial é fundamental para modelar o tempo entre as chegadas ou os tempos de serviço em muitos sistemas. Esse aplicativo é particularmente útil para você:

1. Centros de atendimento ao cliente:

• Modelagem do tempo entre as chamadas recebidas
• Previsão de horários de pico de carga
• Otimização da programação da equipe

2. Telecomunicações:

• Análise de padrões de tráfego de rede
• Modelagem de tempos de chegada de pacotes em redes de dados
• Planejamento da capacidade da rede

3. Sistemas de saúde:

• Modelagem do tempo de chegada de pacientes em departamentos de emergência
• Estimativa de tempos de espera para serviços
• Planejamento da alocação de recursos

A distribuição exponencial funciona bem nesses contextos porque muitos processos de chegada podem ser aproximados como eventos sem memória que ocorrem em uma taxa média constante.

Cálculo de probabilidades com a distribuição exponencial

Ao trabalhar com a distribuição exponencial, temos duas abordagens principais para calcular as probabilidades: a PDF é particularmente útil quando precisamos encontrar a probabilidade de um evento ocorrer em um intervalo ou faixa específica, enquanto a CDF nos ajuda a determinar a probabilidade de um evento ocorrer antes de um determinado momento. Vamos explorar as duas abordagens usando um cenário prático de help desk.

Usando a função de densidade de probabilidade

Mencionamos que o PDF nos ajuda a calcular a probabilidade de ocorrência de um evento em um intervalo. Para distribuições contínuas, como a exponencial, precisamos integrar a PDF ao longo do intervalo de interesse.

Vamos analisar um exemplo prático: Imagine que estamos analisando chamadas de atendimento ao cliente em um help desk em que as chamadas chegam seguindo uma distribuição exponencial com uma taxa média de 3 chamadas por hora (λ = 3).

Para descobrir a probabilidade de esperar entre 10 e 20 minutos pela próxima chamada, faríamos o seguinte:

1. Converta o tempo em horas: (10 minutos = 1/6 hora, 20 minutos = 1/3 hora)
2. Use a fórmula: P(1/6 < X < 1/3) = ∫[1/6 a 1/3] 3e^(-3x)dx
3. Avalie: = -e^{(-3x)|[1/6 a 1/3]}
4. Calcule: = [e^(-0,5) - e^(-1)] ≈ 0,2325 ou cerca de 23,25%

Usando a função de distribuição cumulativa

Dissemos que o CDF é útil quando queremos encontrar a probabilidade de um evento antes de um tempo. Agora, usando nosso exemplo de help desk: Qual é a probabilidade de recebermos uma chamada nos primeiros 15 minutos?

Usando nosso exemplo de help desk: Qual é a probabilidade de recebermos uma chamada nos primeiros 15 minutos?

1. Converta 15 minutos em horas: (15 minutos = 1/4 de hora)
2. Use a fórmula CDF: F(1/4) = 1 - e^(-3*1/4)
3. Calcule: = 1 - e^(-0,75) ≈ 0,5276 ou cerca de 52,76%

Isso significa que há aproximadamente 53% de chance de você receber uma chamada nos primeiros 15 minutos. Observe como o CDF torna esses cálculos de probabilidade "até" mais simples do que usar o PDF.

Visualizando a distribuição exponencial

Vamos primeiro analisar a distribuição exponencial por si só e depois compará-la com outras distribuições.

Representação gráfica

Aqui está um conjunto de gráficos que criei em Python:

Vamos explorar como as fórmulas matemáticas se traduzem em padrões visuais. A visualização mostra três parâmetros de taxa diferentes (0,5, 1,0 e 2,0) para demonstrar como λ molda a distribuição:

Observando o PDF (gráfico superior):

• Quando λ = 2,0 (linha verde), vemos o declínio inicial mais acentuado, começando em f(0) = 2,0. Isso indica que os eventos iniciais são muito mais prováveis
• Quando λ = 1,0 (linha laranja), obtemos a distribuição exponencial padrão com um decaimento mais moderado
• Quando λ = 0,5 (linha vermelha), a curva diminui mais gradualmente, mostrando que tempos de espera mais longos são mais comuns

O CDF (gráfico inferior) conta uma história complementar:

• A taxa mais alta (λ = 2,0) resulta no aumento mais acentuado, mostrando que a probabilidade cumulativa se acumula rapidamente
• A taxa mais baixa (λ = 0,5) mostra um acúmulo mais gradual de probabilidade
• Todas as curvas acabam se aproximando de 1, ilustrando que a probabilidade de ocorrência do evento se aproxima da certeza à medida que o tempo aumenta

Esse comportamento torna a distribuição exponencial particularmente útil para modelar fenômenos do mundo real, como tempos de espera, vida útil de equipamentos e tempo entre eventos em um processo de Poisson.

Comparação com outras distribuições

As características exclusivas da distribuição exponencial ficam mais claras quando comparadas a outras distribuições de probabilidade comuns. Vamos examinar essas comparações por meio de nossa visualização:

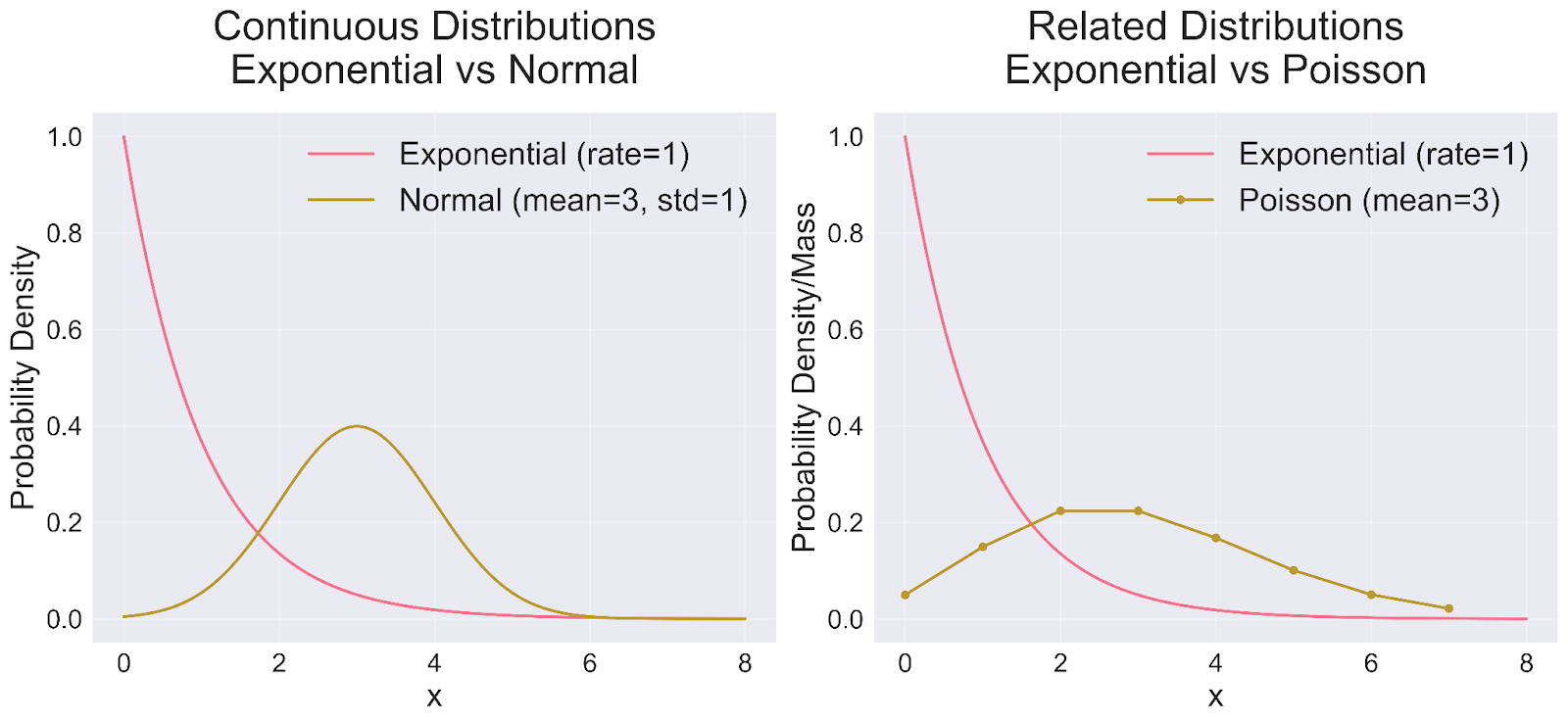
Ao examinar a comparação da distribuição normal (painel esquerdo), surgem várias diferenças importantes. A distribuição exponencial apresenta uma inclinação acentuada para a direita, atingindo seu valor máximo imediatamente antes de diminuir continuamente. Isso contrasta nitidamente com a conhecida curva simétrica em forma de sino da distribuição normal, centralizada em torno de seu valor médio. Embora ambas se qualifiquem como distribuições contínuas, elas servem a propósitos de modelagem distintos: a distribuição exponencial é excelente para modelar tempos de espera e intervalos, enquanto a distribuição normal normalmente lida com medições e médias.

A relação com a distribuição de Poisson (painel direito) revela outra dimensão fascinante da teoria da probabilidade. Enquanto a distribuição exponencial mede o tempo entre os eventos, a distribuição de Poisson concentra-se na contagem do número de eventos em um intervalo fixo. Essas distribuições formam dois lados da mesma moeda: em um processo de Poisson, os tempos de espera seguem naturalmente uma distribuição exponencial. Outra distinção notável está em sua continuidade - a distribuição exponencial pode assumir qualquer valor real positivo, enquanto a distribuição de Poisson lida exclusivamente com números inteiros discretos e não negativos.

Essas percepções comparativas esclarecem por que a distribuição exponencial é excelente em cenários de modelagem específicos. Ela se mostra inestimável ao analisar intervalos de tempo entre eventos aleatórios, oferecendo recursos que vão além do foco de contagem de eventos da distribuição de Poisson. A distribuição se destaca especialmente em cenários que exigem avaliação de probabilidade de ocorrência imediata, em contraste com a abordagem de tendência central da distribuição normal. Talvez o mais importante seja que sua propriedade exclusiva de ausência de memória a diferencia das distribuições Normal e Poisson, tornando-a a escolha ideal para processos em que eventos passados não influenciam as probabilidades futuras.

Equívocos e armadilhas comuns

Ao trabalhar com a distribuição exponencial, várias concepções errôneas comuns podem levar a uma análise incorreta. Compreender essas possíveis armadilhas ajuda a garantir a aplicação precisa da distribuição em cenários do mundo real.

Interpretação incorreta da propriedade sem memória

A propriedade sem memória geralmente causa confusão porque parece contradizer nossa experiência cotidiana. Aqui estão alguns mal-entendidos comuns e suas correções:

Um equívoco frequente é pensar que a propriedade sem memória significa que os eventos passados não têm valor para a previsão. Na realidade, isso significa que a probabilidade de esperar um período de tempo adicional permanece a mesma, independentemente de quanto tempo você já esperou. Por exemplo:

• Interpretação incorreta: "Se uma lâmpada segue uma distribuição exponencial e não falhou em 5 anos, ela deve estar prestes a falhar em breve."
• Interpretação correta: "Se uma lâmpada segue uma distribuição exponencial e não falhou em 5 anos, sua probabilidade de durar mais um ano é a mesma que a de uma lâmpada nova durar um ano."

Outro equívoco envolve presumir que todos os cenários de confiabilidade exibem a propriedade sem memória. Na realidade, muitos sistemas apresentam efeitos de envelhecimento ou padrões de desgaste que não seguem o comportamento exponencial. Por exemplo, os componentes mecânicos geralmente apresentam taxas de falha crescentes ao longo do tempo.

Uso incorreto de parâmetros

Vários erros comuns ocorrem ao selecionar e aplicar o parâmetro de taxa:

1. Taxa vs. confusão média:

   • Um erro comum é usar o valor médio como o parâmetro de taxa (λ)

   • Lembre-se: A média (valor esperado) é, na verdade, 1/λ

   • Por exemplo, se os eventos ocorrem em média a cada 2 horas, λ = 1/2, não 2

2. Incompatibilidade de unidades:

   • O parâmetro de taxa deve ser consistente com as unidades de tempo em seus dados

   • Se você medir o tempo em horas, mas especificar λ em dias^(-1), suas probabilidades estarão incorretas

   • Sempre converta para unidades consistentes antes de aplicar a distribuição

3. Aplicação excessiva:

   • Veracidade de que os eventos ocorrem independentemente

   • Que a taxa permaneça constante ao longo do tempo

   • E que o processo não tem efeitos de memória 

Para evitar esses erros, sempre defina claramente suas unidades e converta-as de forma consistente, verifique se as suposições da distribuição exponencial se ajustam ao seu cenário, teste seus dados quanto ao comportamento exponencial antes de aplicar a distribuição e documente suas escolhas de parâmetros e suas justificativas.

Conclusão

A simplicidade elegante e as aplicações poderosas da distribuição exponencial fazem dela uma ferramenta indispensável no kit de ferramentas de um cientista de dados. Sua propriedade exclusiva de ausência de memória e a relação com outras distribuições, principalmente a distribuição gaussiana, destacam seu lugar especial na teoria da probabilidade.

Embora este guia tenha abordado os aspectos essenciais, sempre há mais a ser explorado em aplicativos especializados. Para os interessados em implementações práticas, nosso curso Simulação estatística em Python oferece experiência prática com esses conceitos. Além disso, a compreensão de como a distribuição exponencial se relaciona com outras distribuições de probabilidade, conforme detalhado em Multivariate Probability Distributions in R (Distribuições de probabilidade multivariada em R), oferece uma perspectiva mais ampla de sua função na modelagem estatística. Independentemente de você estar analisando dados de sobrevivência, modelando a confiabilidade do sistema ou estudando comportamentos de fila, o domínio da distribuição exponencial abre novas possibilidades na análise de dados e na modelagem estatística.