Comprendre la distribution exponentielle : Un guide complet

Comprendre les distributions de probabilités est fondamental pour la science des données, et parmi celles-ci, je trouve que la distribution exponentielle se distingue par des caractéristiques uniques qui méritent d'être explorées. Bien qu'elle partage des liens mathématiques avec la distribution de Poisson, la distribution exponentielle modélise uniquement les intervalles de temps entre les événements plutôt que le nombre d'événements. 

Pour ceux qui découvrent les concepts de probabilité, notre cours Fondements des probabilités en Python fournit des connaissances de base essentielles. Les applications pratiques de la distribution exponentielle s'étendent à divers domaines, de l'ingénierie de la fiabilité à la théorie des files d'attente, ce qui la rend particulièrement précieuse dans des domaines tels que l'analyse de survie, qui est explorée en profondeur dans Survival Analysis in Python. Ce guide explore les concepts fondamentaux, les bases mathématiques et les applications concrètes de la distribution exponentielle, vous permettant ainsi d'acquérir les connaissances nécessaires pour l'appliquer efficacement dans vos projets de science des données.

Qu'est-ce que la distribution exponentielle ?

La distribution exponentielle est une distribution de probabilité continue qui modélise le temps entre les événements dans un processus où les événements se produisent continuellement et indépendamment à un taux moyen constant. Il est particulièrement utile pour analyser des situations impliquant des temps d'attente, des durées de vie et des intervalles entre les événements.

Imaginez que vous travaillez dans un centre de service à la clientèle très actif. Le temps écoulé entre les appels entrants des clients suit souvent une distribution exponentielle. De même, dans l'industrie manufacturière, le temps qui s'écoule avant qu'une machine ne tombe en panne ou ne doive être entretenue présente souvent un comportement exponentiel.

Principales caractéristiques de la distribution exponentielle

La distribution exponentielle possède plusieurs propriétés uniques qui la rendent particulièrement utile dans les applications du monde réel :

La propriété d'absence de mémoire

C'est peut-être la caractéristique la plus distinctive de la distribution exponentielle. Cela signifie que le comportement futur du système ne dépend pas de son histoire passée. Par exemple, si une ampoule a déjà duré 1000 heures, la probabilité qu'elle dure encore 100 heures est la même que si elle était neuve. Cette propriété est propre à la distribution exponentielle parmi les distributions continues.

Taux d'aléa constant

La distribution exponentielle maintient un taux de défaillance constant dans le temps. Cela signifie que la probabilité qu'un événement se produise dans le prochain petit intervalle de temps reste la même, quel que soit le temps écoulé.

La relation entre les distributions exponentielle et de Poisson est fondamentale dans la théorie des probabilités. Alors que la distribution de Poisson modélise le nombre d'événements survenant dans un intervalle de temps fixe, la distribution exponentielle modélise le temps entre ces événements. Ce sont les deux faces d'une même pièce : si les événements se produisent selon un processus de Poisson avec un taux λ, alors le temps d'attente entre les événements suit une distribution exponentielle avec un paramètre λ.

Formulation mathématique

La distribution exponentielle est définie par un seul paramètre λ (lambda), qui représente le paramètre de taux. Examinons ses principales composantes mathématiques :

Fonction de densité de probabilité (PDF)

Le PDF nous aide à calculer la probabilité qu'un événement se produise dans un intervalle spécifique. La PDF de la distribution exponentielle est la suivante :   

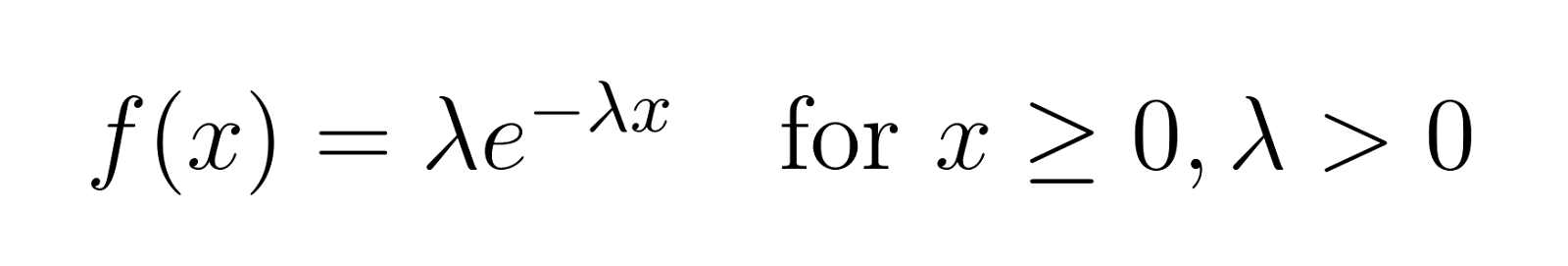
   où :

• x est la variable aléatoire (représentant généralement le temps)
• λ est le paramètre de taux (λ > 0)
• e est le nombre d'Euler (environ 2,71828)

Fonction de distribution cumulative (FDC)

La FCD est particulièrement utile lorsque l'on souhaite connaître la probabilité qu'un événement se produise avant un certain temps. Il nous donne la probabilité que le temps d'attente soit inférieur ou égal à une valeur spécifique. Voici la fonction de distribution cumulative de la distribution exponentielle :

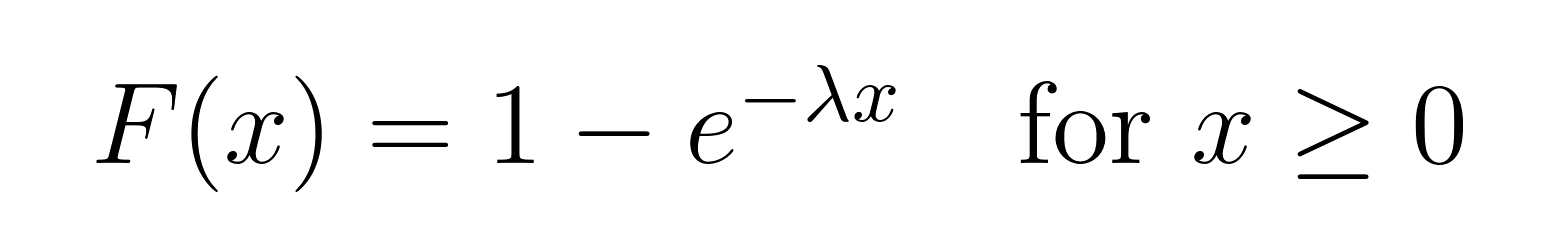
Applications de la distribution exponentielle

La distribution exponentielle joue un rôle essentiel dans divers domaines, en nous aidant à modéliser et à comprendre les processus dépendant du temps. Examinons quelques-unes de ses principales applications. 

Ingénierie de la fiabilité

L'ingénierie de la fiabilité s'appuie fortement sur la distribution exponentielle pour modéliser la durée de vie des composants et des systèmes. Cette méthode est particulièrement utile en raison de la propriété "sans mémoire" de la distribution : la durée de vie future d'un composant ne dépend que du présent, et non de sa durée de fonctionnement.

Par exemple, les composants électroniques présentent généralement des temps de défaillance distribués de manière exponentielle, ce qui démontre la propriété unique d'absence de mémoire de cette distribution. Cela signifie qu'un nouveau microprocesseur a la même probabilité de tomber en panne dans l'heure qui suit qu'un microprocesseur qui a fonctionné pendant un mois (en supposant qu'il n'y ait pas d'effets d'usure). Les fabricants de matériel de serveur utilisent largement cette distribution dans leurs analyses de fiabilité pour calculer le temps moyen entre les pannes (MTBF), déterminer les programmes de maintenance optimaux et prévoir les coûts de garantie et les besoins de remplacement. Ces informations sont précieuses pour le développement des produits et la planification des activités.

Théorie des files d'attente

Dans la théorie des files d'attente, la distribution exponentielle est fondamentale pour modéliser le temps entre les arrivées ou les temps de service dans de nombreux systèmes. Cette application est particulièrement utile dans les cas suivants

1. Centres de service à la clientèle :

• Modélisation du temps entre les appels entrants
• Prévoir les heures de pointe
• Optimisation de la planification du personnel

2. Télécommunications :

• Analyse des schémas de trafic du réseau
• Modélisation des temps d'arrivée des paquets dans les réseaux de données
• Planification de la capacité du réseau

3. Systèmes de santé :

• Modélisation des temps d'arrivée des patients dans les services d'urgence
• Estimation des temps d'attente pour les services
• Planification de l'affectation des ressources

La distribution exponentielle fonctionne bien dans ces contextes car de nombreux processus d'arrivée peuvent être approximés comme des événements sans mémoire se produisant à un taux moyen constant.

Calcul des probabilités avec la distribution exponentielle

Lorsque l'on travaille avec la distribution exponentielle, on dispose de deux approches principales pour calculer les probabilités : la PDF est particulièrement utile lorsqu'il s'agit de déterminer la probabilité qu'un événement se produise dans un intervalle ou une plage spécifique, tandis que la CDF nous aide à déterminer la probabilité qu'un événement se produise avant un certain point dans le temps. Explorons ces deux approches à l'aide d'un scénario pratique de service d'assistance.

En utilisant la fonction de densité de probabilité

Nous avons mentionné que le PDF nous aide à calculer la probabilité qu'un événement se produise dans un intervalle. Pour les distributions continues comme l'exponentielle, nous devons intégrer la PDF sur l'intervalle qui nous intéresse.

Prenons un exemple concret : Imaginons que nous analysions les appels au service clientèle d'un centre d'assistance où les appels arrivent selon une distribution exponentielle avec un taux moyen de 3 appels par heure (λ = 3).

Pour trouver la probabilité d'attendre entre 10 et 20 minutes pour le prochain appel, nous devrions :

1. Convertir le temps en heures : (10 minutes = 1/6 heure, 20 minutes = 1/3 heure)
2. Utilisez la formule: P(1/6 < X < 1/3) = ∫[1/6 à 1/3] 3e^(-3x)dx
3. Évaluez: = -e^{(-3x)|[1/6 à 1/3]}
4. Calculer: = [e^(-0,5) - e^(-1)] ≈ 0,2325 ou environ 23,25%.

En utilisant la fonction de distribution cumulative

Nous avons dit que la FCD est utile lorsque nous voulons trouver la probabilité d'un événement avant un certain temps. Reprenons l'exemple de notre service d'assistance : Quelle est la probabilité que nous recevions un appel dans les 15 premières minutes ?

Reprenons l'exemple de notre service d'assistance : Quelle est la probabilité que nous recevions un appel dans les 15 premières minutes ?

1. Convertir 15 minutes en heures : (15 minutes = 1/4 d'heure)
2. Utilisez la formule CDF: F(1/4) = 1 - e^(-3*1/4)
3. Calculez: = 1 - e^(-0,75) ≈ 0,5276 ou environ 52,76%.

Cela signifie qu'il y a environ 53 % de chances de recevoir un appel dans les 15 premières minutes. Remarquez que la FCD rend ces calculs de probabilité "jusqu'à" plus simples que l'utilisation de la PDF.

Visualisation de la distribution exponentielle

Examinons d'abord la distribution exponentielle en tant que telle, puis comparons-la à d'autres distributions.

Représentation graphique

Voici un ensemble de graphiques que j'ai créés en Python :

Voyons comment les formules mathématiques se traduisent en motifs visuels. La visualisation montre trois paramètres de taux différents (0,5, 1,0 et 2,0) pour démontrer comment λ façonne la distribution :

En examinant le PDF (graphique du haut) :

• Lorsque λ = 2,0 (ligne verte), on observe la baisse initiale la plus forte, à partir de f(0) = 2,0. Cela indique que les événements précoces sont beaucoup plus susceptibles
• Lorsque λ = 1,0 (ligne orange), nous obtenons la distribution exponentielle standard avec une décroissance plus modérée.
• Lorsque λ = 0,5 (ligne rouge), la courbe diminue plus graduellement, ce qui montre que les temps d'attente plus longs sont plus fréquents.

La fonction de distribution cumulative (graphique du bas) est complémentaire :

• Le taux le plus élevé (λ = 2,0) donne lieu à l'augmentation la plus forte, ce qui montre que la probabilité cumulée s'accumule rapidement.
• Le taux le plus bas (λ = 0,5) montre une accumulation plus graduelle de la probabilité.
• Toutes les courbes finissent par se rapprocher de 1, ce qui montre que la probabilité que l'événement se produise se rapproche de la certitude au fur et à mesure que le temps s'écoule

Ce comportement rend la distribution exponentielle particulièrement utile pour modéliser des phénomènes réels tels que les temps d'attente, les durées de vie des équipements et le temps entre les événements d'un processus de Poisson.

Comparaison avec d'autres distributions

Les caractéristiques uniques de la distribution exponentielle apparaissent plus clairement lorsqu'on la compare à d'autres distributions de probabilités courantes. Examinons ces comparaisons à l'aide de notre visualisation :

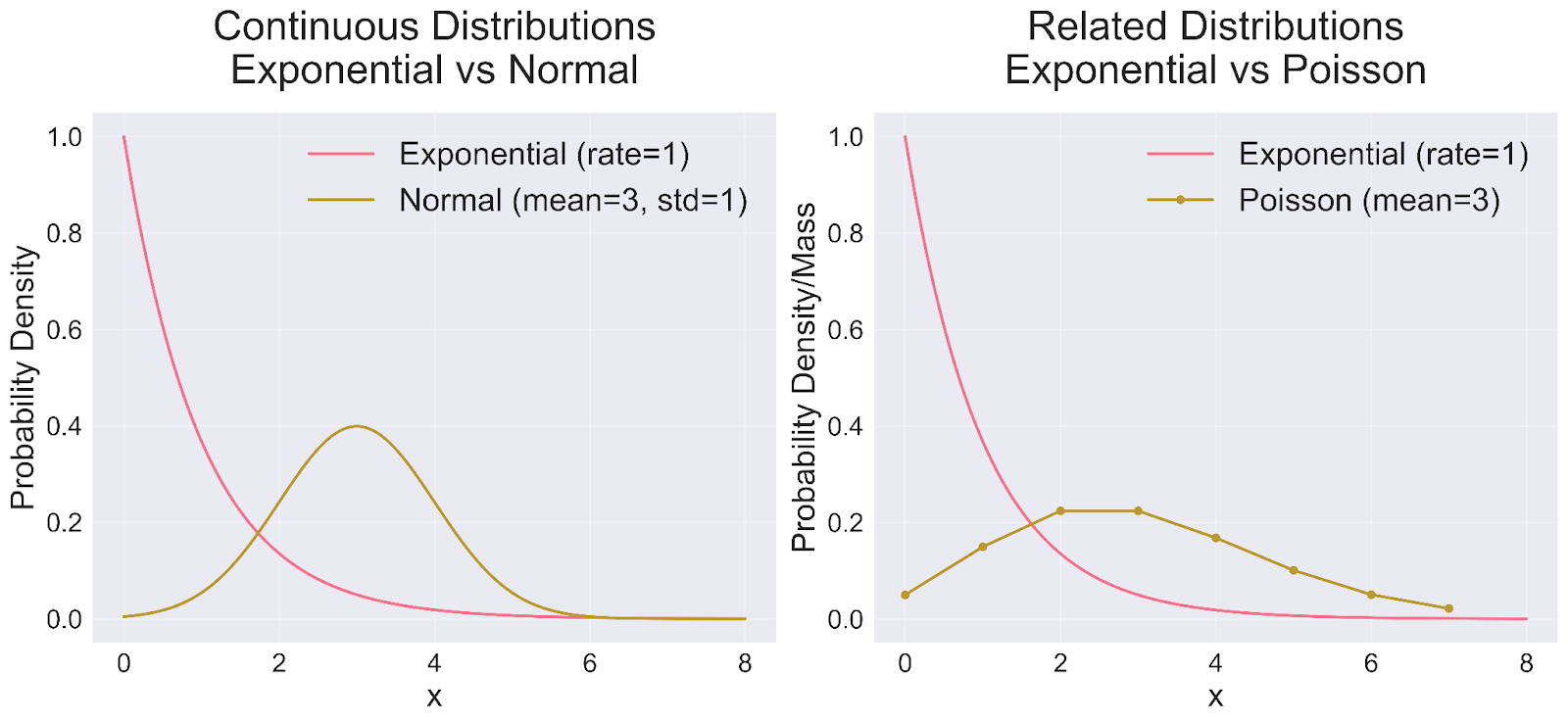
L'examen de la comparaison de la distribution normale (panneau de gauche) fait apparaître plusieurs différences essentielles. La distribution exponentielle présente une asymétrie prononcée vers la droite, atteignant sa valeur maximale immédiatement avant de diminuer continuellement. Cela contraste fortement avec la courbe symétrique en forme de cloche de la distribution normale, centrée autour de sa valeur moyenne. Bien qu'il s'agisse dans les deux cas de distributions continues, elles servent des objectifs de modélisation distincts : la distribution exponentielle excelle dans la modélisation des temps d'attente et des intervalles, tandis que la distribution normale traite généralement des mesures et des moyennes.

La relation avec la distribution de Poisson (panneau de droite) révèle une autre dimension fascinante de la théorie des probabilités. Alors que la distribution exponentielle mesure le temps écoulé entre les événements, la distribution de Poisson se concentre sur le comptage du nombre d'événements dans un intervalle fixe. Ces distributions constituent les deux faces d'une même pièce : dans un processus de Poisson, les temps d'attente suivent naturellement une distribution exponentielle. Une autre distinction notable réside dans leur continuité : la distribution exponentielle peut prendre n'importe quelle valeur réelle positive, tandis que la distribution de Poisson ne concerne que des nombres entiers discrets et non négatifs.

Ces comparaisons permettent de comprendre pourquoi la distribution exponentielle excelle dans des scénarios de modélisation spécifiques. Elle s'avère inestimable pour l'analyse des intervalles de temps entre les événements aléatoires, car elle offre des possibilités qui vont au-delà du comptage d'événements de la distribution de Poisson. La distribution s'avère particulièrement efficace dans les scénarios exigeant une évaluation immédiate des probabilités d'occurrence, ce qui contraste avec l'approche de la tendance centrale de la distribution normale. Sa propriété unique d'absence de mémoire la distingue des distributions normales et de Poisson, ce qui en fait le choix optimal pour les processus dans lesquels les événements passés n'influencent pas les probabilités futures.

Idées fausses et pièges courants

Lorsque vous travaillez avec la distribution exponentielle, plusieurs idées fausses courantes peuvent conduire à une analyse incorrecte. La compréhension de ces pièges potentiels permet d'assurer une application précise de la distribution dans des scénarios réels.

Mauvaise interprétation de la propriété d'absence de mémoire

La propriété d'absence de mémoire est souvent source de confusion car elle semble contredire notre expérience quotidienne. Voici les malentendus les plus courants et leurs corrections :

Une erreur fréquente consiste à penser que la propriété d'absence de mémoire signifie que les événements passés n'ont aucune valeur prédictive. En réalité, cela signifie que la probabilité d'attendre un délai supplémentaire reste la même, quelle que soit la durée de l'attente. Par exemple :

• Interprétation erronée: "Si une ampoule suit une distribution exponentielle et qu'elle n'est pas tombée en panne depuis 5 ans, elle doit être sur le point de tomber en panne.
• Interprétation correcte: "Si une ampoule suit une distribution exponentielle et n'est pas tombée en panne depuis 5 ans, sa probabilité de durer encore un an est la même que celle d'une nouvelle ampoule qui durerait un an."

Une autre idée fausse consiste à supposer que tous les scénarios de fiabilité présentent la propriété d'absence de mémoire. En réalité, de nombreux systèmes présentent des effets de vieillissement ou des schémas d'usure qui ne suivent pas un comportement exponentiel. Par exemple, les composants mécaniques présentent souvent des taux de défaillance croissants au fil du temps.

Utilisation incorrecte des paramètres

Plusieurs erreurs courantes sont commises lors de la sélection et de l'application du paramètre de taux :

1. Confusion entre le taux et la moyenne:

   • Une erreur fréquente consiste à utiliser la valeur moyenne comme paramètre de taux (λ)

   • Rappelez-vous : La moyenne (valeur attendue) est en fait 1/λ

   • Par exemple, si les événements se produisent en moyenne toutes les 2 heures, λ = 1/2, et non 2

2. Inadéquation de l'unité:

   • Le paramètre de taux doit être cohérent avec les unités de temps de vos données.

   • Si vous mesurez le temps en heures mais que vous spécifiez λ en jours^(-1), vos probabilités seront incorrectes.

   • Convertissez toujours en unités cohérentes avant d'appliquer la distribution

3. Sur-application:

   • Vérité que les événements se produisent indépendamment les uns des autres

   • Que le taux reste constant dans le temps

   • Et que le processus n'a pas d'effets de mémoire 

Pour éviter ces erreurs, définissez toujours clairement vos unités et convertissez-les de manière cohérente, vérifiez que les hypothèses de la distribution exponentielle correspondent à votre scénario, testez le comportement exponentiel de vos données avant d'appliquer la distribution, et documentez vos choix de paramètres et leur justification.

Conclusion

L'élégante simplicité de la distribution exponentielle et ses puissantes applications en font un outil indispensable dans la boîte à outils d'un scientifique des données. Sa propriété unique d'absence de mémoire et sa relation avec d'autres distributions, en particulier la distribution gaussienne, soulignent la place particulière qu'elle occupe dans la théorie des probabilités.

Bien que ce guide ait couvert les aspects essentiels, il y a toujours plus à explorer dans les applications spécialisées. Pour ceux qui s'intéressent aux mises en œuvre pratiques, notre cours Simulation statistique en Python offre une expérience pratique de ces concepts. En outre, la compréhension de la relation entre la distribution exponentielle et d'autres distributions de probabilités, telle que détaillée dans Multivariate Probability Distributions in R, offre une perspective plus large sur son rôle dans la modélisation statistique. Que vous analysiez des données de survie, modélisiez la fiabilité d'un système ou étudiiez le comportement des files d'attente, la maîtrise de la distribution exponentielle ouvre de nouvelles possibilités en matière d'analyse de données et de modélisation statistique.