¿Qué es la normalización en el aprendizaje automático? Guía completa para el reescalado de datos

En el aprendizaje automático, la base del éxito de los modelos es la calidad de los datos con los que se entrenan. Aunque a menudo los focos se centran en algoritmos y modelos complejos y sofisticados, el héroe olvidado suele ser el preprocesamiento de datos. El preprocesamiento de datos es un paso importante que transforma los datos brutos en características que luego se utilizan para un aprendizaje automático eficaz.

Los algoritmos de aprendizaje automático suelen entrenarse suponiendo que todas las características contribuyen por igual a la predicción final. Sin embargo, esta suposición falla cuando los rasgos difieren en rango y unidad, lo que afecta a su importancia.

Entra en la normalización, un paso vital en el preprocesamiento de datos que garantiza la uniformidad de las magnitudes numéricas de las características. Esta uniformidad evita la dominación de rasgos que tienen valores mayores en comparación con los demás rasgos o variables.

En este artículo, nos sumergiremos en la normalización, una técnica de escalado de características que ofrece una vía para equilibrar la balanza de las características.

¿Qué es la Normalización?

La normalización es una forma específica de escalado de rasgos que transforma la gama de rasgos a una escala estándar. La normalización y, para el caso, cualquier técnica de escalado de datos sólo es necesaria cuando tu conjunto de datos tiene características de rangos variables. La normalización engloba diversas técnicas adaptadas a diferentes distribuciones de datos y requisitos del modelo.

La normalización no se limita sólo a los datos numéricos. Sin embargo, en este artículo nos centraremos en ejemplos numéricos. No dejes de consultar Textacy de Datacamp: Una introducción a la limpieza y normalización de datos de texto en el tutorial de Python si estás pensando en realizar un preprocesamiento de datos de texto para el aprendizaje automático.

¿Por qué normalizar los datos?

Los datos normalizados aumentan el rendimiento del modelo y mejoran su precisión. Ayuda a los algoritmos que se basan en métricas de distancia, como k-vecinos más próximos o máquinas de vectores de apoyo, evitando que los rasgos con escalas mayores dominen el proceso de aprendizaje.

La normalización fomenta la estabilidad en el proceso de optimización, promoviendo una convergencia más rápida durante el entrenamiento basado en el gradiente. Mitiga los problemas relacionados con la desaparición o explosión de gradientes, permitiendo que los modelos alcancen soluciones óptimas de forma más eficiente.

Los datos normalizados también son fáciles de interpretar y, por tanto, de comprender. Cuando todas las características de un conjunto de datos están a la misma escala, también resulta más fácil identificar y visualizar las relaciones entre las distintas características y hacer comparaciones significativas.

Pongamos un ejemplo sencillo para resaltar la importancia de normalizar los datos. Intentamos predecir los precios de la vivienda basándonos en diversas características, como los metros cuadrados, el número de dormitorios, la distancia al supermercado, etc. El conjunto de datos contiene características diversas con escalas variables, como:

• Metros cuadrados: Rangos de 500 a 5000 pies cuadrados
• Número de habitaciones: Rangos de 1 a 5
• Distancia al supermercado: Rangos de 0,1 a 16 km

Cuando introduces estos datos sin ningún preprocesamiento directamente en un modelo de aprendizaje automático, el algoritmo podría dar más peso a las características con escalas grandes, como los metros cuadrados. Durante el entrenamiento, el algoritmo supone que un cambio en los metros cuadrados totales tendrá un impacto significativo en los precios de la vivienda. El algoritmo podría pasar por alto los matices de características que son relativamente pequeñas, como el número de habitaciones y la distancia al supermercado. Este énfasis sesgado puede conducir a un rendimiento subóptimo del modelo y a predicciones sesgadas.

Normalizando los rasgos, podemos garantizar que cada rasgo contribuye proporcionalmente al proceso de aprendizaje del modelo. Ahora el modelo puede aprender patrones de todas las características con mayor eficacia, lo que conduce a una representación más precisa de las relaciones subyacentes en los datos.

Resumen de las técnicas de normalización

El escalado Mín-Máx y la normalización de la puntuación Z (estandarización) son las dos técnicas fundamentales de normalización. Aparte de éstos, también hablaremos de la normalización de escala decimal, la normalización de escala logarítmica y el escalado robusto, que abordan retos únicos en el preprocesamiento de datos.

Escalado Mín-Máx

El escalado mínimo-máximo se suele llamar simplemente "normalización". Transforma los rasgos en un intervalo especificado, normalmente entre 0 y 1. La fórmula para el escalado mín-máx es:

_Xnormalizado = X - _Xmín / _Xmáx - _Xmín

Donde X es un valor aleatorio de la característica que hay que normalizar. _Xmin es el valor mínimo de la característica en el conjunto de datos, y _Xmax es el valor máximo de la característica.

• Cuando X es el valor mínimo, el numerador es cero (_Xmín - _Xmín) y, por tanto, el valor normalizado es 0
• Cuando X es el valor máximo, el numerador es igual al denominador (_Xmax - _Xmin) y, por tanto, el valor normalizado es 1
• Cuando X no es ni mínimo ni máximo, el valor normalizado está entre 0 y 1. Es lo que se denomina técnica de escalado min-max

El escalado mínimo-máximo es una buena opción cuando:

• Se conocen los límites superior e inferior aproximados del conjunto de datos, y el conjunto de datos tiene pocos o ningún valor atípico
• Cuando la distribución de los datos es desconocida o no gaussiana, y los datos se distribuyen aproximadamente de forma uniforme en el intervalo
• Cuando es esencial mantener la forma original de la distribución

Normalización de la puntuación Z (estandarización)

La normalización (estandarización) de la puntuación Z supone una distribución gaussiana (curva de campana) de los datos y transforma los rasgos para que tengan una media (μ) de 0 y una desviación típica (σ) de 1. La fórmula de la normalización es

_{Xestandarizado} = X-μ / σ

​Esta técnica es especialmente útil cuando se trata de algoritmos que suponen datos distribuidos normalmente, como muchos modelos lineales. A diferencia de la técnica de escalado mín-máx, en la técnica de normalización los valores de los rasgos no están restringidos a un rango concreto. Esta técnica de normalización representa básicamente las características en función del número de desviaciones típicas que se alejan de la media.

Antes de profundizar en otras técnicas de transformación de datos, vamos a realizar una comparación de la normalización (escalado mín-máx) y la estandarización.

Normalización de la escala decimal

El objetivo de la normalización de escala decimal es escalar los valores de los rasgos en una potencia de 10, garantizando que el mayor valor absoluto de cada rasgo sea menor que 1. Es útil cuando se conoce el rango de valores de un conjunto de datos, pero el rango varía según las características. La fórmula para la normalización de la escala decimal es:

X_decimal = X / 10^d

Donde X es el valor original de la característica, y d es el menor número entero tal que el mayor valor absoluto de la característica sea menor que 1.

Por ejemplo, si el mayor valor absoluto de una característica es 3500, entonces d sería 3, y la característica se escalaría en¹⁰³.

La normalización de la escala decimal es ventajosa cuando se trata de conjuntos de datos en los que la magnitud absoluta de los valores importa más que su escala específica.

Normalización de la escala logarítmica

La normalización de escala logarítmica convierte los datos en una escala logarítmica, tomando el logaritmo de cada punto de datos. Es especialmente útil cuando se trata de datos que abarcan varios órdenes de magnitud. La fórmula para la normalización de la escala logarítmica es:

_Xlog = log(X)

Esta normalización resulta útil con datos que siguen un patrón de crecimiento o decaimiento exponencial. Comprime la escala del conjunto de datos, facilitando que los modelos capten patrones y relaciones en los datos. El tamaño de la población a lo largo de los años es un buen ejemplo de conjunto de datos en el que algunas características muestran un crecimiento exponencial. La normalización de la escala logarítmica puede hacer que estos rasgos sean más aptos para el modelado.

Normalización robusta de la escala

La normalización robusta de la escala es útil cuando se trabaja con conjuntos de datos que tienen valores atípicos. Utiliza la mediana y el rango intercuartílico (IQR) en lugar de la media y la desviación típica para tratar los valores atípicos. La fórmula del escalado robusto es

_Xrobusto = X - mediana/ IQR

Como el escalado robusto es resistente a la influencia de valores atípicos, resulta adecuado para conjuntos de datos con valores sesgados o anómalos.

Errores comunes de normalización y buenas prácticas

Hemos hablado de la normalización y de por qué es útil en el aprendizaje automático. Aunque potente, la normalización no está exenta de dificultades. Desde la gestión de los valores atípicos hasta la selección de la técnica más adecuada en función de tu conjunto de datos, abordar estas cuestiones es esencial para liberar todo el potencial de tu modelo de aprendizaje automático.

Manejo de valores atípicos

Los valores atípicos son puntos de datos de tu conjunto de datos que se desvían significativamente de la norma y distorsionan la eficacia de las técnicas de normalización. Si no manejas los valores atípicos de tus datos, éstos pueden dar lugar a transformaciones sesgadas. Puedes trabajar con la técnica de normalización de escala robusta que hemos comentado antes para tratar los valores atípicos.

Otra estrategia consiste en aplicar el recorte o winsorizado, en el que identificamos y recortamos o limitamos a un valor fijo todos los valores de las características por encima (o por debajo) de un determinado valor.

Elección de la técnica de normalización

Hemos hablado de las técnicas de normalización más útiles, pero hay muchas más entre las que elegir. Seleccionar la técnica adecuada requiere una comprensión matizada del conjunto de datos. Al preprocesar los datos, tienes que probar varias técnicas de normalización y evaluar su impacto en el rendimiento del modelo. La experimentación te permite observar cómo influye cada método en el proceso de aprendizaje.

Necesitas conocer a fondo las características de los datos. Considera si los supuestos de una técnica de normalización concreta se ajustan a la distribución y los patrones presentes en el conjunto de datos.

Normalización de datos dispersos

La normalización puede ser un reto cuando se trata de datos dispersos en los que muchos valores de características son cero. Aplicar directamente técnicas de normalización estándar puede tener consecuencias no deseadas. Hay versiones de las técnicas de normalización de las que hemos hablado antes que están diseñadas específicamente para datos dispersos, como el "escalado min-max disperso".

Antes de la normalización, considera la posibilidad de imputar o tratar los valores perdidos en tu conjunto de datos. Éste suele ser uno de los primeros pasos cuando exploras tu conjunto de datos y lo limpias para utilizarlo en modelos de aprendizaje automático.

Asegúrate de consultar el curso de Ingeniería de Características para el Aprendizaje Automático de DataCamp, que te proporciona experiencia práctica sobre cómo preparar cualquier dato para tus propios modelos de aprendizaje automático. En el curso, trabajarás con la encuesta a desarrolladores de Stack Overflow y con direcciones históricas de inauguraciones presidenciales de EE.UU. para comprender cuál es la mejor forma de preprocesar e ingeniar características a partir de datos categóricos, continuos y no estructurados.

Normalización y riesgo de sobreajuste

En el aprendizaje automático, el sobreajuste se produce cuando un modelo no sólo aprende los patrones subyacentes en los datos de entrenamiento, sino que también capta el ruido y las fluctuaciones aleatorias. Esto puede dar lugar a un modelo que funcione excepcionalmente bien con los datos de entrenamiento, pero que no se generalice a los nuevos datos no vistos.

La normalización por sí sola puede no causar sobreajuste. Sin embargo, cuando la normalización se combina con otros factores, como la complejidad del modelo o una regularización insuficiente, puede contribuir al sobreajuste. Cuando los parámetros de normalización se calculan utilizando todo el conjunto de datos (incluidos los conjuntos de validación o de prueba), puede producirse una fuga de datos. El modelo podría aprender inadvertidamente información de los conjuntos de validación o de prueba, comprometiendo su capacidad de generalización.

Por tanto, para mitigar el riesgo de sobreajuste, normaliza el conjunto de entrenamiento y aplica los mismos parámetros de normalización a los conjuntos de validación y de prueba. Esto garantiza que el modelo aprenda a generalizar a partir de los datos de entrenamiento sin verse influido por la información de los conjuntos de validación o prueba.

Necesitas aplicar técnicas de regularización adecuadas para penalizar los modelos demasiado complejos. La regularización ayuda a evitar que el modelo se adapte al ruido de los datos de entrenamiento. Utiliza técnicas de validación adecuadas, como la validación cruzada, para evaluar el rendimiento del modelo en datos no vistos. Si se detecta sobreajuste durante la validación, se pueden hacer ajustes, como reducir la complejidad del modelo o aumentar la regularización.

Implementar la Normalización en Python con Scikit-learn

Scikit-learn es una versátil biblioteca de Python diseñada para simplificar las complejidades del aprendizaje automático. Proporciona un rico conjunto de herramientas y funcionalidades para el preprocesamiento de datos, la selección de características, la reducción de la dimensionalidad, la construcción y el entrenamiento de modelos, la evaluación de modelos, el ajuste de hiperparámetros, la serialización de modelos, la construcción de canalizaciones, etc. Su diseño modular fomenta la experimentación y la exploración, permitiendo a los usuarios pasar sin problemas de los conceptos fundamentales a las metodologías avanzadas.

Utilizaremos scikit-learn para poner en práctica lo aprendido. Utilizaremos el clásico y ampliamente utilizado `conjunto de datos de Iris.` Este conjunto de datos fue introducido por el biólogo y estadístico británico Ronald A. Fisher en 1936. El conjunto de datos Iris comprende mediciones de cuatro características de tres especies distintas de flores de iris: setosa, versicolor y virginica.

En cada flor se miden cuatro características, que son la longitud del sépalo, la anchura del sépalo, la longitud del pétalo y la anchura del pétalo, todas ellas en centímetros. Hay 150 instancias (muestras) en el conjunto de datos, con 50 muestras de cada una de las tres especies. El conjunto de datos Iris se suele utilizar para tareas de clasificación, en las que el objetivo es predecir la especie correcta entre las tres clases. Sin embargo, hoy utilizaremos este conjunto de datos para mostrar la transformación de los datos al aplicar la normalización (escala mín-máx) y la estandarización. 

Puedes ejecutar el código Python que se describe a continuación en el espacio de trabajo de Datacamp para explorar tú mismo el conjunto de datos.

Empecemos por importar las bibliotecas que necesitamos....

import numpy as np
import pandas as pd
# To import the dataset
from sklearn.datasets import load_iris
# To be used for splitting the dataset into training and test sets
from sklearn.model_selection import train_test_split
# To be used for min-max normalization
from sklearn.preprocessing import MinMaxScaler
# To be used for Z-normalization (standardization)
from sklearn.preprocessing import StandardScaler

# Load the iris dataset from Scikit-learn package
iris = load_iris()

# This prints a summary of the characteristics, statistics of the dataset
print(iris.DESCR)
 
# Divide the data into features (X) and target (Y)
# Data is converted to a panda’s dataframe
X = pd.DataFrame(iris.data)
 
# Separate the target attribute from rest of the data columns
Y = iris.target
 
# Take a look at the dataframe
X.head()
 
# This prints the shape of the dataframe (150 rows and 4 columns)
X.shape()

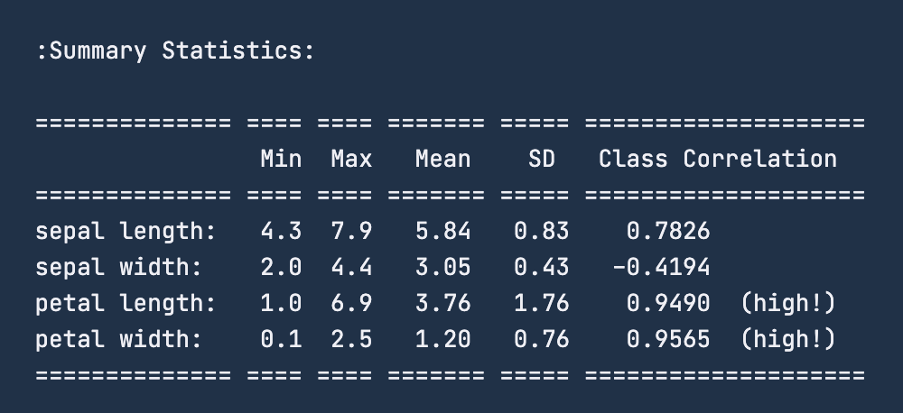
Cuando consultes las estadísticas resumidas de los datos utilizando print(iris.DESCR), la imagen siguiente es el resumen que recibirás. Para el rasgo "longitud del sépalo", el intervalo es de 4,3 - 7,9 centímetros. Del mismo modo, para la "anchura del sépalo", el intervalo es de 2 a 4,4 centímetros. Para la "longitud de los pétalos", el intervalo es de 1 a 6,9 centímetros y, por último, para la "anchura de los pétalos", el intervalo es de 0,1 a 2,5 centímetros.

Antes de aplicar la normalización, es una buena práctica dividir el conjunto de datos en conjuntos de entrenamiento y de prueba. Para ello utilizaremos la funcionalidad train_test_split de sklearn.model_selection. No vamos a crear un conjunto de validación, ya que en este ejercicio no vamos a realizar un modelado real de aprendizaje automático. Haremos una división 80-20 del conjunto de datos, lo que significa que el conjunto de entrenamiento tendrá 120 filas, y el de prueba tendrá el resto, 30 puntos de datos.

# To divide the dataset into training and test sets

X_train, X_test, y_train, y_test = train_test_split(X, Y ,test_size=0.2)

Un paso habitual tras cargar los datos y dividirlos en un conjunto de entrenamiento-prueba es realizar la limpieza de datos, la imputación de datos para tratar los valores perdidos y los valores atípicos de los datos. Sin embargo, como el artículo se centra en la normalización, nos saltaremos estos pasos de preprocesamiento y pasaremos a ver la normalización en acción.

Ahora transformaremos estos datos para que entren en el intervalo de 0 - 1 centímetro utilizando la técnica de normalización mín-máx. Para normalizar los datos, utilizaremos la funcionalidad MinMaxScaler de la biblioteca sklearn y la aplicaremos a nuestro conjunto de datos; ya hemos importado antes las bibliotecas necesarias.

# Good practice to keep original dataframes untouched for reusability
X_train_n = X_train.copy()
X_test_n = X_test.copy()
 
# Fit min-max scaler on training data
norm = MinMaxScaler().fit(X_train_n)
 
# Transform the training data
X_train_norm = norm.transform(X_train_n)
 
# Use the same scaler to transform the testing set
X_test_norm = norm.transform(X_test_n)

Podemos imprimir los datos de entrenamiento para ver la transformación que se ha producido. Sin embargo, convirtamos el conjunto en un marco de datos pandas y comprobemos después su descripción estadística utilizando la funcionalidad describe().

X_train_norm_df = pd.DataFrame(X_train_norm)
 
     	# Assigning original feature names for ease of read
X_train_norm_df.columns = iris.feature_names
 
X_train_norm_df.describe()

Esto dará el siguiente resultado para la normalización:

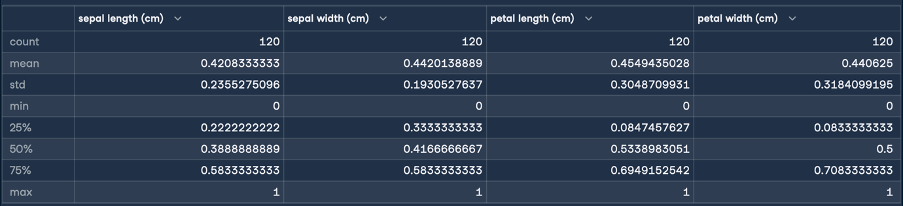
Aquí, las estadísticas mín. y máx. indican que los rangos de los rasgos se han transformado todos a un rango de 0 - 1 centímetro. ¡Ésta es la transformación que pretendíamos! Ahora realizaremos la estandarización (normalización de la puntuación Z) siguiendo los mismos pasos que para la normalización:

X_train_s = X_train.copy()
X_test_s = X_test.copy()
 
# Fit the standardization scaler onto the training data
stan = StandardScaler().fit(X_train_s)
 
# Transform the training data
X_train_stan = stan.transform(X_train_s)
 
# Use the same scaler to transform the testing set
X_test_stan = stan.transform(X_test_s)
 
     	# Convert the transformed data into pandas dataframe
X_train_stan_df = pd.DataFrame(X_train_stan)
 
     	# Assigning original feature names for ease of read
X_train_stan_df.columns = iris.feature_names
 
     	# Check out the statistical description
X_train_stan_df.describe()

Esto dará el siguiente resultado para la normalización:

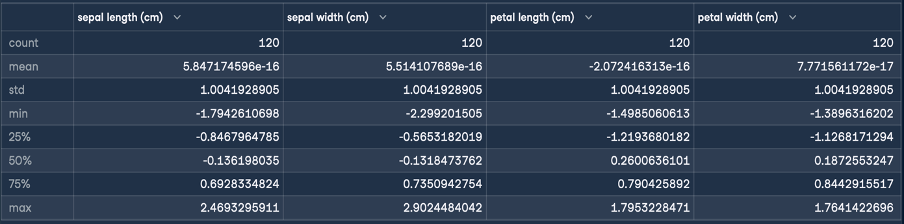
El objetivo de la normalización Z es transformar los valores de una característica para que tengan una media de 0 y una desviación típica de 1. Como puedes ver en la descripción de la trama de datos que se generó, la media de las cuatro características es un número pequeño cercano a cero, y la desviación típica es 1.

Ahora podemos tomar estos datos transformados e introducirlos en un algoritmo de aprendizaje automático para su entrenamiento.

Reflexiones finales

En este artículo, hemos recorrido las normalizaciones de escala mín-máx, normalización Z, escala decimal y escala logarítmica. Cada técnica reveló sus puntos fuertes y su utilidad únicos. También has leído sobre algunos de los escollos más comunes y las mejores prácticas al realizar la normalización. Por último, terminamos aplicando algunos de estos conocimientos recién adquiridos, con scikit learn.

Para saber más sobre los conceptos y procesos que hemos tratado, consulta nuestros cursos sobre Ingeniería de Características para el Aprendizaje Automático en Python y Textacy: Introducción a la limpieza y normalización de datos de texto en Python.