Qu'est-ce que la normalisation dans l'apprentissage automatique ? Un guide complet sur le redimensionnement des données

Dans le domaine de l'apprentissage automatique, le succès des modèles repose sur la qualité des données sur lesquelles ils sont formés. Alors que les projecteurs sont souvent braqués sur des algorithmes et des modèles complexes et sophistiqués, le héros méconnu est souvent le prétraitement des données. Le prétraitement des données est une étape importante qui transforme les données brutes en caractéristiques qui sont ensuite utilisées pour un apprentissage automatique efficace.

Les algorithmes d'apprentissage automatique sont souvent formés en partant du principe que toutes les caractéristiques contribuent de manière égale à la prédiction finale. Toutefois, cette hypothèse ne tient pas lorsque les caractéristiques diffèrent en termes de portée et d'unité, ce qui affecte leur importance.

La normalisation est une étape essentielle du prétraitement des données qui garantit l'uniformité des valeurs numériques des caractéristiques. Cette uniformité permet d'éviter la domination des caractéristiques dont les valeurs sont plus élevées que celles des autres caractéristiques ou variables.

Dans cet article, nous allons nous pencher sur la normalisation, une technique de mise à l'échelle des caractéristiques qui permet d'équilibrer la balance des caractéristiques.

Qu'est-ce que la normalisation ?

La normalisation est une forme spécifique de mise à l'échelle des caractéristiques qui transforme la gamme des caractéristiques en une échelle standard. La normalisation et, d'ailleurs, toute technique de mise à l'échelle des données n'est nécessaire que lorsque votre ensemble de données comporte des caractéristiques de portée variable. La normalisation englobe diverses techniques adaptées aux différentes distributions de données et aux exigences des modèles.

La normalisation ne se limite pas aux données numériques. Toutefois, dans cet article, nous nous concentrerons sur des exemples numériques. Ne manquez pas de consulter le site Textacy de DataCamp : Une introduction au nettoyage et à la normalisation des données textuelles en tutoriel Python si vous envisagez d'effectuer un prétraitement sur des données textuelles pour l'apprentissage automatique.

Pourquoi normaliser les données ?

Les données normalisées améliorent la performance et la précision du modèle. Il aide les algorithmes qui s'appuient sur des mesures de distance, comme les voisins les plus proches ou les machines à vecteurs de support, en empêchant les caractéristiques à grande échelle de dominer le processus d'apprentissage.

La normalisation favorise la stabilité du processus d'optimisation, ce qui permet d'accélérer la convergence lors de l'apprentissage basé sur le gradient. Il atténue les problèmes liés à l'évanouissement ou à l'explosion des gradients, ce qui permet aux modèles d'atteindre des solutions optimales plus efficacement.

Les données normalisées sont également faciles à interpréter et donc à comprendre. Lorsque toutes les caractéristiques d'un ensemble de données sont à la même échelle, il devient également plus facile d'identifier et de visualiser les relations entre les différentes caractéristiques et de faire des comparaisons significatives.

Prenons un exemple simple pour souligner l'importance de la normalisation des données. Nous essayons de prédire les prix des logements sur la base de diverses caractéristiques telles que la superficie, le nombre de chambres, la distance par rapport au supermarché, etc. L'ensemble de données contient diverses caractéristiques à différentes échelles, telles que

• Superficie en mètres carrés : Gamme de 500 à 5000 pieds carrés
• Nombre de chambres à coucher : Fourchette de 1 à 5
• Distance du supermarché : Fourchette de 0,1 à 10 milles

Lorsque vous introduisez ces données sans aucun prétraitement directement dans un modèle d'apprentissage automatique, l'algorithme peut accorder plus de poids aux caractéristiques à grande échelle, telles que le nombre de pieds carrés. Lors de l'apprentissage, l'algorithme suppose qu'une variation de la superficie totale aura un impact significatif sur les prix des logements. L'algorithme peut négliger les nuances de caractéristiques relativement petites, telles que le nombre de chambres à coucher et la distance par rapport au supermarché. Cet accent biaisé peut conduire à une performance sous-optimale du modèle et à des prédictions biaisées.

En normalisant les caractéristiques, nous pouvons nous assurer que chaque caractéristique contribue proportionnellement au processus d'apprentissage du modèle. Le modèle peut désormais apprendre des modèles à travers toutes les caractéristiques de manière plus efficace, ce qui conduit à une représentation plus précise des relations sous-jacentes dans les données.

Techniques de normalisation en un coup d'œil

L'échelle Min-Max et la normalisation du score Z (standardisation) sont les deux techniques fondamentales de normalisation. En outre, nous discuterons également de la normalisation de l'échelle décimale, de la normalisation de l'échelle logarithmique et de l'échelle robuste, qui répondent à des défis uniques en matière de prétraitement des données.

Échelle Min-Max

La mise à l'échelle minimale-maximale est très souvent appelée simplement "normalisation". Il transforme les caractéristiques en une plage spécifiée, généralement entre 0 et 1. La formule d'échelonnement min-max est la suivante :

_Xnormalisé = X - _Xmin / _Xmax - _Xmin

Où X est une valeur aléatoire qui doit être normalisée. _Xmin est la valeur minimale de la caractéristique dans l'ensemble de données et _Xmax est la valeur maximale de la caractéristique.

• Lorsque X est la valeur minimale, le numérateur est égal à zéro (_Xmin - _Xmin) et la valeur normalisée est donc égale à 0.
• Lorsque X est la valeur maximale, le numérateur est égal au dénominateur (_Xmax - _Xmin) et la valeur normalisée est donc 1.
• Lorsque X n'est ni minimum ni maximum, la valeur normalisée est comprise entre 0 et 1. C'est ce qu'on appelle la technique d'échelonnement min-max.

L'échelle minimale-maximale est un bon choix lorsque :

• Les limites inférieures et supérieures approximatives de l'ensemble de données sont connues et l'ensemble de données ne comporte que peu ou pas de valeurs aberrantes.
• Lorsque la distribution des données est inconnue ou non gaussienne, et que les données sont approximativement distribuées de manière uniforme dans l'intervalle
• Lorsqu'il est essentiel de conserver la forme originale de la distribution

Normalisation du score Z (standardisation)

La normalisation du score Z (standardisation) suppose une distribution gaussienne (courbe en cloche) des données et transforme les caractéristiques pour qu'elles aient une moyenne (μ) de 0 et un écart type (σ) de 1. La formule de la normalisation est la suivante :

_{Xstandardized} = X-μ / σ

​Cette technique est particulièrement utile lorsqu'il s'agit d'algorithmes qui supposent des données normalement distribuées, comme de nombreux modèles linéaires. Contrairement à la technique de mise à l'échelle min-max, les valeurs des caractéristiques ne sont pas limitées à une plage spécifique dans la technique de normalisation. Cette technique de normalisation représente essentiellement les caractéristiques en termes de nombre d'écarts types par rapport à la moyenne.

Avant d'aborder d'autres techniques de transformation des données, comparons la normalisation (mise à l'échelle min-max) et la standardisation.

Normalisation de l'échelle décimale

L'objectif de la normalisation par échelle décimale est de mettre à l'échelle les valeurs des caractéristiques par une puissance de 10, en veillant à ce que la plus grande valeur absolue de chaque caractéristique devienne inférieure à 1. Elle est utile lorsque l'éventail des valeurs d'un ensemble de données est connu, mais que cet éventail varie d'une caractéristique à l'autre. La formule de normalisation de l'échelle décimale est la suivante :

_Xdécimal = X / ^10d

Où X est la valeur de l'élément original et d est le plus petit nombre entier tel que la plus grande valeur absolue de l'élément devienne inférieure à 1.

Par exemple, si la plus grande valeur absolue d'une caractéristique est 3500, d sera égal à 3 et la caractéristique sera mise à l'échelle par¹⁰³.

La normalisation de l'échelle décimale est avantageuse lorsqu'il s'agit d'ensembles de données où la magnitude absolue des valeurs importe plus que leur échelle spécifique.

Normalisation de l'échelle logarithmique

La normalisation par échelle logarithmique convertit les données en une échelle logarithmique, en prenant le logarithme de chaque point de données. Elle est particulièrement utile lorsqu'il s'agit de données qui s'étendent sur plusieurs ordres de grandeur. La formule de normalisation de l'échelle logarithmique est la suivante :

X_log = log(X)

Cette normalisation est très utile pour les données qui suivent un modèle de croissance ou de décroissance exponentielle. Il comprime l'échelle de l'ensemble des données, ce qui permet aux modèles de saisir plus facilement les schémas et les relations dans les données. La taille de la population au fil des ans est un bon exemple d'ensemble de données où certaines caractéristiques présentent une croissance exponentielle. La normalisation par échelle logarithmique peut rendre ces caractéristiques plus faciles à modéliser.

Normalisation robuste de l'échelle

La normalisation robuste de l'échelle est utile lorsque vous travaillez avec des ensembles de données comportant des valeurs aberrantes. Il utilise la médiane et l'intervalle interquartile (IQR) au lieu de la moyenne et de l'écart type pour traiter les valeurs aberrantes. La formule pour une mise à l'échelle robuste est la suivante :

_Xrobust = X - médiane/ IQR

La mise à l'échelle robuste étant résistante à l'influence des valeurs aberrantes, elle convient aux ensembles de données présentant des valeurs asymétriques ou anormales.

Pièges et bonnes pratiques en matière de normalisation

Nous avons discuté de la normalisation et de son utilité dans l'apprentissage automatique. Bien que puissante, la normalisation n'est pas sans poser de problèmes. De la gestion des valeurs aberrantes à la sélection de la technique la plus appropriée en fonction de votre ensemble de données, il est essentiel de traiter ces questions pour libérer tout le potentiel de votre modèle d'apprentissage automatique.

Traitement des valeurs aberrantes

Les valeurs aberrantes sont des points de données dans votre ensemble de données qui s'écartent de manière significative de la norme et faussent l'efficacité des techniques de normalisation. Si vous ne traitez pas les valeurs aberrantes de vos données, celles-ci peuvent conduire à des transformations asymétriques. Vous pouvez utiliser la technique de normalisation robuste de l'échelle dont nous avons parlé précédemment pour traiter les valeurs aberrantes.

Une autre stratégie consiste à appliquer un élagage ou une winsorisation, c'est-à-dire à identifier et à écrêter ou plafonner toutes les valeurs de caractéristiques supérieures (ou inférieures) à une certaine valeur pour les ramener à une valeur fixe.

Choix de la technique de normalisation

Nous avons abordé les techniques de normalisation les plus utiles, mais il en existe beaucoup d'autres. Le choix de la technique appropriée nécessite une compréhension nuancée de l'ensemble des données. Lors du prétraitement des données, vous devez essayer plusieurs techniques de normalisation et évaluer leur impact sur la performance du modèle. L'expérimentation vous permet d'observer comment chaque méthode influence le processus d'apprentissage.

Vous devez acquérir une connaissance approfondie des caractéristiques des données. Examinez si les hypothèses d'une technique de normalisation spécifique correspondent à la distribution et aux modèles présents dans l'ensemble de données.

Normalisation sur des données éparses

La normalisation peut s'avérer difficile lorsqu'il s'agit de données éparses où de nombreuses valeurs de caractéristiques sont nulles. L'application directe de techniques de normalisation standard peut avoir des conséquences inattendues. Il existe des versions des techniques de normalisation que nous avons examinées plus haut qui sont spécifiquement conçues pour les données éparses, comme le "sparse min-max scaling" (mise à l'échelle min-max éparse).

Avant de procéder à la normalisation, envisagez d'imputer ou de traiter les valeurs manquantes dans votre ensemble de données. C'est souvent l'une des premières étapes lorsque vous explorez votre ensemble de données et que vous le nettoyez pour l'utiliser dans des modèles d'apprentissage automatique.

Assurez-vous de consulter le cours Feature Engineering for Machine Learning de DataCamp, qui vous donne une expérience pratique sur la façon de préparer n'importe quelles données pour vos propres modèles d'apprentissage automatique. Dans ce cours, vous travaillerez avec l'enquête Stack Overflow Developers et les adresses historiques des inaugurations présidentielles américaines pour comprendre comment mieux prétraiter et concevoir des caractéristiques à partir de données catégoriques, continues et non structurées.

Normalisation et risque de surajustement

Dans le domaine de l'apprentissage automatique, on parle d'overfitting lorsqu'un modèle apprend non seulement les schémas sous-jacents des données d'apprentissage, mais aussi le bruit et les fluctuations aléatoires. Cela peut conduire à un modèle qui donne des résultats exceptionnels sur les données d'apprentissage, mais qui ne parvient pas à se généraliser à de nouvelles données inédites.

La normalisation seule n'entraîne pas nécessairement un surajustement. Cependant, lorsque la normalisation est combinée à d'autres facteurs, tels que la complexité du modèle ou une régularisation insuffisante, elle peut contribuer à un surajustement. Lorsque les paramètres de normalisation sont calculés en utilisant l'ensemble des données (y compris les ensembles de validation ou de test), il peut en résulter une fuite de données. Le modèle peut apprendre par inadvertance des informations provenant des ensembles de validation ou de test, ce qui compromet sa capacité de généralisation.

Ainsi, pour réduire le risque d'ajustement excessif, normalisez l'ensemble d'apprentissage et appliquez les mêmes paramètres de normalisation aux ensembles de validation et de test. Cela garantit que le modèle apprend à généraliser à partir des données d'apprentissage sans être influencé par les informations contenues dans les ensembles de validation ou de test.

Vous devez mettre en œuvre des techniques de régularisation appropriées pour pénaliser les modèles trop complexes. La régularisation permet d'éviter que le modèle ne s'adapte au bruit dans les données d'apprentissage. Utilisez des techniques de validation appropriées, telles que la validation croisée, pour évaluer les performances du modèle sur des données inédites. Si un surajustement est détecté au cours de la validation, des ajustements peuvent être effectués, par exemple en réduisant la complexité du modèle ou en augmentant la régularisation.

Implémentation de la normalisation en Python avec Scikit-learn

Scikit-learn est une bibliothèque Python polyvalente conçue pour simplifier les complexités de l'apprentissage automatique. Il fournit un ensemble riche d'outils et de fonctionnalités pour le prétraitement des données, la sélection des caractéristiques, la réduction de la dimensionnalité, la construction et l'entraînement des modèles, l'évaluation des modèles, l'ajustement des hyperparamètres, la sérialisation des modèles, la construction de pipelines, etc. Sa conception modulaire encourage l'expérimentation et l'exploration, permettant aux utilisateurs de passer en douceur des concepts fondamentaux aux méthodologies avancées.

Nous utiliserons scikit-learn pour mettre en pratique ce que nous avons appris. Cet ensemble de données a été introduit par le biologiste et statisticien britannique Ronald A. Fisher en 1936. L'ensemble de données Iris comprend des mesures de quatre caractéristiques provenant de trois espèces différentes de fleurs d'iris : setosa, versicolor et virginica.

Quatre caractéristiques sont mesurées pour chaque fleur : la longueur et la largeur du sépale, la longueur et la largeur du pétale, le tout en centimètres. L'ensemble de données comprend 150 instances (échantillons), soit 50 échantillons pour chacune des trois espèces. L'ensemble de données Iris est généralement utilisé pour des tâches de classification, l'objectif étant de prédire la bonne espèce parmi les trois classes. Cependant, aujourd'hui, nous utiliserons cet ensemble de données pour montrer la transformation des données lors de l'application de la normalisation (échelle min-max) et de la standardisation. 

Vous pouvez exécuter le code Python ci-dessous dans l' espace de travail de DataCamp pour explorer vous-même l'ensemble de données.

Commençons par importer les bibliothèques dont nous avons besoin....

import numpy as np
import pandas as pd
# To import the dataset
from sklearn.datasets import load_iris
# To be used for splitting the dataset into training and test sets
from sklearn.model_selection import train_test_split
# To be used for min-max normalization
from sklearn.preprocessing import MinMaxScaler
# To be used for Z-normalization (standardization)
from sklearn.preprocessing import StandardScaler

# Load the iris dataset from Scikit-learn package
iris = load_iris()

# This prints a summary of the characteristics, statistics of the dataset
print(iris.DESCR)
 
# Divide the data into features (X) and target (Y)
# Data is converted to a panda’s dataframe
X = pd.DataFrame(iris.data)
 
# Separate the target attribute from rest of the data columns
Y = iris.target
 
# Take a look at the dataframe
X.head()
 
# This prints the shape of the dataframe (150 rows and 4 columns)
X.shape()

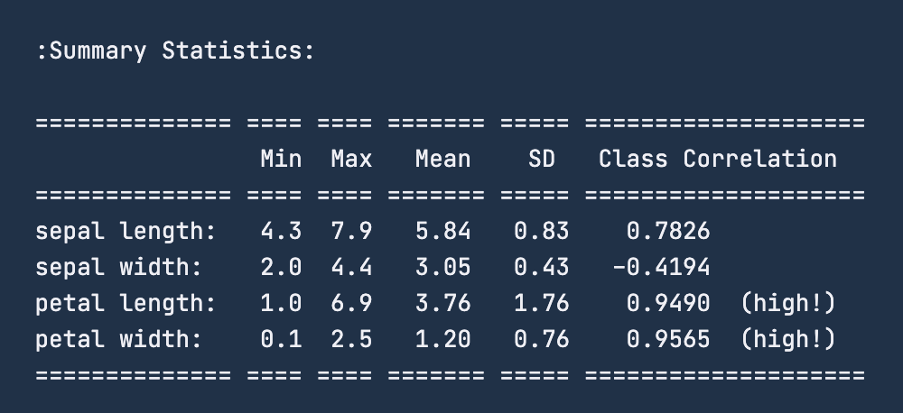
Lorsque vous consultez les statistiques récapitulatives des données à l'aide de print(iris.DESCR), l'image ci-dessous est le résumé que vous obtiendrez. Pour la caractéristique "longueur du sépale", la fourchette est comprise entre 4,3 et 7,9 centimètres. De même, pour la "largeur des sépales", la fourchette est comprise entre 2 et 4,4 centimètres. Pour la "longueur des pétales", la fourchette est de 1 à 6,9 centimètres et, enfin, pour la "largeur des pétales", la fourchette est de 0,1 à 2,5 centimètres.

Avant d'appliquer la normalisation, il est conseillé de diviser l'ensemble de données en ensembles de formation et de test. Pour ce faire, nous utiliserons la fonctionnalité train_test_split de sklearn.model_selection. Nous ne définissons pas d'ensemble de validation puisque nous n'effectuerons pas de modélisation d'apprentissage automatique dans le cadre de cet exercice. Nous diviserons l'ensemble de données en 80-20, ce qui signifie que l'ensemble d'entraînement comportera 120 lignes et que l'ensemble de test comportera les 30 points de données restants.

# To divide the dataset into training and test sets

X_train, X_test, y_train, y_test = train_test_split(X, Y ,test_size=0.2)

Après avoir chargé les données et les avoir divisées en un ensemble de formation et de test, l'étape habituelle consiste à nettoyer les données, à les imputer pour traiter les valeurs manquantes et les données aberrantes. Cependant, comme l'article se concentre sur la normalisation, nous allons sauter ces étapes de prétraitement et passer à la normalisation en action.

Nous allons maintenant transformer ces données pour qu'elles soient comprises entre 0 et 1 centimètre en utilisant la technique de normalisation min-max. Pour normaliser les données, nous utiliserons la fonctionnalité MinMaxScaler de la bibliothèque sklearn et l'appliquerons à notre ensemble de données ; nous avons déjà importé les bibliothèques nécessaires précédemment.

# Good practice to keep original dataframes untouched for reusability
X_train_n = X_train.copy()
X_test_n = X_test.copy()
 
# Fit min-max scaler on training data
norm = MinMaxScaler().fit(X_train_n)
 
# Transform the training data
X_train_norm = norm.transform(X_train_n)
 
# Use the same scaler to transform the testing set
X_test_norm = norm.transform(X_test_n)

Nous pouvons imprimer les données d'apprentissage pour voir la transformation qui s'est produite. Cependant, convertissons l'ensemble en un dataframe pandas, puis vérifions sa description statistique à l'aide de la fonctionnalité describe().

X_train_norm_df = pd.DataFrame(X_train_norm)
 
     	# Assigning original feature names for ease of read
X_train_norm_df.columns = iris.feature_names
 
X_train_norm_df.describe()

Vous obtiendrez ainsi le résultat suivant pour la normalisation :

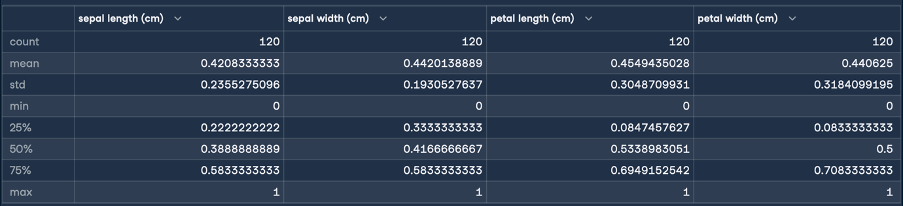
Ici, les statistiques min et max indiquent que les plages des caractéristiques ont toutes été transformées en une plage de 0 à 1 centimètre. C'est la transformation que nous voulions ! Nous allons maintenant procéder à la normalisation (normalisation du score Z) en suivant les mêmes étapes que pour la normalisation :

X_train_s = X_train.copy()
X_test_s = X_test.copy()
 
# Fit the standardization scaler onto the training data
stan = StandardScaler().fit(X_train_s)
 
# Transform the training data
X_train_stan = stan.transform(X_train_s)
 
# Use the same scaler to transform the testing set
X_test_stan = stan.transform(X_test_s)
 
     	# Convert the transformed data into pandas dataframe
X_train_stan_df = pd.DataFrame(X_train_stan)
 
     	# Assigning original feature names for ease of read
X_train_stan_df.columns = iris.feature_names
 
     	# Check out the statistical description
X_train_stan_df.describe()

Cela donne le résultat suivant pour la normalisation :

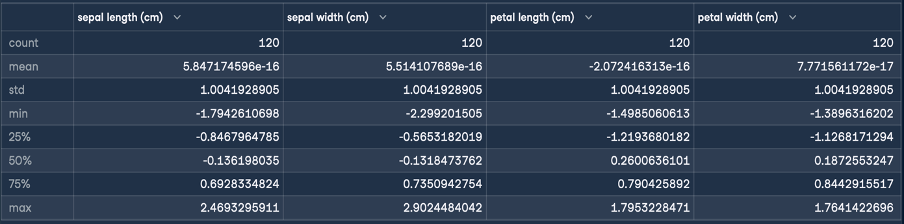
L'objectif de la normalisation Z est de transformer les valeurs d'une caractéristique pour qu'elles aient une moyenne de 0 et un écart-type de 1. Comme vous pouvez le voir dans la description du DataFrame généré, la moyenne des quatre caractéristiques est un petit nombre proche de zéro, et l'écart type est de 1.

Nous pouvons maintenant utiliser ces données transformées et les transmettre à un algorithme d'apprentissage automatique à des fins de formation.

Réflexions finales

Dans cet article, nous avons abordé les normalisations de l'échelle min-max, de la normalisation Z, de l'échelle décimale et de l'échelle logarithmique. Chaque technique a révélé ses propres forces et son utilité. Vous avez également pris connaissance des pièges les plus courants et des meilleures pratiques en matière de normalisation. Enfin, nous avons terminé en appliquant certaines de ces connaissances nouvellement acquises à l'aide de scikit learn.

Pour en savoir plus sur les concepts et les processus que nous avons abordés, consultez nos cours sur l'ingénierie des fonctionnalités pour l'apprentissage automatique en Python et Textacy : Une introduction au nettoyage et à la normalisation des données textuelles en Python.