Gurobi : Optimisation mathématique pour les problèmes complexes

Les solveurs de base et les méthodes d'essais et d'erreurs rencontrent des difficultés lorsque les variables augmentent. Gurobi gère ces complexités avec rapidité et précision, résolvant en quelques secondes des problèmes qui pourraient autrement prendre des heures. C'est la différence entre espérer un plan réalisable et prouver mathématiquement que vous avez le plan optimal.

Ce tutoriel vous guideà travers le puissant solveur commercial connu sous le nom de Gurobi . Je vais vous expliquer comment installer la bibliothèque Python, formuler votre premier modèle et passer à des problèmes plus complexes tels que la programmation mixte en nombres entiers.

Comprendre l'optimisation mathématique et le rôle de Gurobi

Avant de commencer à écrire du code, il est utile de comprendre ce que signifie réellement l'optimisation. Ce contexte vous indique quand utiliser Gurobi plutôt que des approches de programmation standard.

Qu'est-ce que l'optimisation mathématique ?

L'optimisation mathématique identifie la solution la plus appropriée parmi toutes les solutions possibles. Vous définissez ce que signifie « optimal » (minimiser les coûts, maximiser les profits, minimiser le temps), ce que vous contrôlez (variables décisionnelles) et les limites auxquelles vous êtes confronté (contraintes). L'optimiseur examine les solutions possibles afin de déterminer la solution optimale.

Cela diffère de la programmation traditionnelle, où l'on spécifie des étapes précises. Avec l'optimisation, vous décrivez le problème mathématiquement et laissez le solveur déterminer comment le résoudre. Vous n'écrivez pas une logique « si ceci, alors cela », vous définissez des relations et laissez les algorithmes trouver les meilleures valeurs.

L'importance de Gurobi dans l'optimisation

Pourquoi Gurobi se distingue

Gurobi est régulièrement classé parmi les optimiseurs commerciaux les plus rapides disponibles. Les tests de performance démontrent souvent qu'il surpasse considérablement les alternatives open source sur les problèmes à grande échelle. Cette rapidité est importante lorsque vous effectuez des optimisations toutes les heures ou lorsque vous avez besoin de résultats dans des délais stricts.

Adoption par l'industrie

Des entreprises issues des secteurs de la logistique, de la finance, de l'énergie et de la santé utilisent Gurobi pour leurs systèmes de production. FedEx optimise ses itinéraires de livraison, tandis que les sociétés financières allouent des milliards à leurs portefeuilles. Les entreprises énergétiques planifient la production d'électricité. Il ne s'agit pas d'exercices théoriques, mais de systèmes qui gèrent de l'argent réel et des contraintes réelles.

Capacités du solveur

Gurobi prend en charge la programmation linéaire (LP), la programmation mixte-entière (MIP), la programmation quadratique (QP) et bien plus encore. Il comprend des algorithmes de pointe tels que l'optimisation simultanée, où plusieurs méthodes de résolution fonctionnent en parallèle et la plus rapide est retenue. Vous bénéficiez de fiabilité et de rapidité sans avoir à sélectionner manuellement les algorithmes.

Configuration de Gurobi

L'installation de Gurobi ne nécessite que quelques étapes. Une fois configuré, il fonctionne de manière transparente avecPython .

Installation et configuration

Veuillez télécharger et installer

Veuillez vous rendresur le site Web de Gurobi et télécharger le programme d'installation adapté à votre système d'exploitation. Il comprend l'optimiseur, l'interface d'gurobipy s et la documentation. Veuillez exécuter le programme d'installationavec les paramètres par défaut, sauf si vous avez besoin d'un chemin d'accès personnalisé.

Après l'installation, veuillez vérifier que tout fonctionne correctement :

import gurobipy as gp
print(f"Gurobi version: {gp.__version__}")

Ici, nous vérifions l'installation en affichant le numéro de version. Une impression réussie confirme que votre environnement est prêt.

Options de licence

Gurobi nécessite une licence pour toute utilisation au-delà de petits problèmes de test. Vos options :

• Licence d'essai gratuite : Évaluation de 30 jours. Veuillez en faire la demande sur le site Web de Gurobi en utilisant votre adresse électronique professionnelle.
• Licence académique : Gratuit pour les enseignants et les étudiants. Veuillez vérifier votre adresse e-mail universitaire pour bénéficier d'un accès illimité, idéal pour l'apprentissage.
• Licence commerciale : Nécessaire pour les activités commerciales. Les tarifs varient en fonction de l'échelle. Les licences nominatives conviennent aux scientifiques des données individuels, tandis que les licences flottantes permettent aux équipes de partager les capacités.
• Licence cloud : Pay-as-you-go. Aucun coût initial, vous ne payez que ce que vous utilisez. Utile pour les tâches d'optimisation occasionnelles.

J'utilise la licence académique pour l'apprentissage et la licence commerciale pour la production. La période d'essai vous offre suffisamment de temps pour explorer avant de vous engager.

Configuration de l'environnement

Configuration Python

Gurobi est compatible avec Python 3.7 et versions ultérieures. Je recommande l'utilisation d'un environnement virtuel afin d'éviter les conflits :

python -m venv gurobi_env
gurobi_env\Scripts\activate
source gurobi_env/bin/activate
pip install gurobipy

Ces commandes permettent de configurer un espace de travail propre et d'importer la bibliothèque.

Intégration de Jupyter Notebook

Pour le développement interactif, les notebooks fonctionnent parfaitement avec Gurobi :

pip install jupyter
jupyter notebook
import gurobipy as gp
print("Gurobi ready!")

Cet extrait installe Jupyter, lance le serveur et effectue une vérification rapide pour s'assurer que Gurobi se charge correctement dans le notebook.

Quand ne pas utiliser Gurobi

Gurobi est un outil puissant, mais il ne constitue pas toujours le choix le plus approprié.

• Problèmes simples: Si vous disposez de 50 variables et de contraintes linéaires de base, des solveurs gratuits tels que scipy.optimize.linprog ou Excel Solverfonctionnent parfaitement.

• Coût: Les licences commerciales sont coûteuses. Pour les outils internes non critiques, des options open source telles que CBC ou GLPK (via PuLP) pourraient être suffisantes.

• Heuristique: Si vous avez besoin d'une réponse « suffisamment bonne » en quelques millisecondes pour un jeu en temps réel, les heuristiques (telles que les algorithmes génétiques) surpassent souvent les solveurs exacts.

Veuillez utiliser Gurobi lorsque les problèmes sont complexes (plus de 10 000 variables) ou lorsque vous avez besoin de fonctionnalités avancées telles que les contraintes quadratiques.

Compatibilité de la plateforme

Gurobi est compatible avec Windows, macOS et Linux. Les environnements cloud tels qu'AWS, Azure et Google Cloud prennent en charge Gurobi via leurs places de marché. J'ai déployé des modèles Gurobi sur les trois principaux clouds sans rencontrer de problèmes spécifiques à une plateforme.

Modèles d'optimisation des bâtiments

Une fois Gurobi installé, nous allons créer votre premier modèle. Ces concepts fondamentaux s'appliquent à tous les problèmes que vous rencontrerez.

Éléments clés d'un modèle d'optimisation

Chaque modèle comporte trois éléments essentiels :

Variables de décision

Ce sont les choix effectués par l'optimiseur. Dans la planification de la production, il peut s'agir des « unités du produit A » et des « unités du produit B ». Vous définissez les variables ; Gurobi attribue les valeurs.

Fonction objective

Il s'agit de votre objectif, ce que vous souhaitez maximiser ou minimiser. Maximiser les bénéfices (3*product_a + 5*product_b) ou minimiser les coûts. Vous recevez un objectif par modèle.

Contraintes

Ce sont vos limites. Il n'est pas possible de produire au-delà de la capacité de l'usine ni de dépenser plus que votre budget. Les contraintes déterminent quelles solutions sont réellement possibles.

Meilleures pratiques en matière de formulation

Veuillez utiliser des noms de variables clairs. Au lieu de x[1], veuillez utiliser produce_product_a. Cela vous évitera de passer des heures à déboguer par la suite, comme je l'expliquerai dans la section consacrée au dépannage.

Veuillez garder les contraintes simples. Décomposer une logique complexe en contraintes plus petites et plus simples facilite la lecture et le débogage de votre modèle.

Gurobi moderne : L'API Matrix

Si vous avez une formation en science des données, la modélisation basée sur des boucles peut vous sembler lente. Gurobi 13.0+ propose une API Matrix qui utilise des tableaux NumPy, ce qui accélère la création de modèles de 10 à 50 fois.

Voici à quoi ressemble un modèle de boulangerie utilisant des vecteurs :

import gurobipy as gp
import numpy as np

# Data
prices = np.array([2.0, 5.0])
resources = np.array([[0.5, 2.0], [1.0, 1.0]])
limits = np.array([100.0, 80.0])

model = gp.Model("bakery_matrix")
x = model.addMVar(shape=2, name="x")

model.setObjective(prices @ x, gp.GRB.MAXIMIZE)
model.addConstr(resources @ x <= limits, name="constraints")

model.optimize()

Cette syntaxe A @ x <= b est plus claire et conforme aux normes des systèmes de production.

Création d'un modèle de programmation linéaire simple

Résolvons un problème pratique : une boulangerie doit déterminer le nombre de pains et de gâteaux à cuire afin de maximiser ses bénéfices.

Problème posé:

- Bénéfice sur le pain : 2 $ | Farine : 0,5 kg

- Bénéfice sur le gâteau : 5 $ | Farine : deux kilogrammes

- Farine disponible : 100 kg

- Capacité du four : 80 articles

Voici le modèle :

import gurobipy as gp
from gurobipy import GRB

model = gp.Model("bakery_optimization")

bread = model.addVar(name="bread", vtype=GRB.CONTINUOUS, lb=0)
cake = model.addVar(name="cake", vtype=GRB.CONTINUOUS, lb=0)

model.setObjective(2 * bread + 5 * cake, GRB.MAXIMIZE)

model.addConstr(0.5 * bread + 2 * cake <= 100, name="flour_limit")
model.addConstr(bread + cake <= 80, name="oven_capacity")

model.optimize()

if model.status == GRB.OPTIMAL:
    print(f"Optimal profit: ${model.objVal:.2f}")
    print(f"Bake {bread.X:.2f} loaves of bread")
    print(f"Bake {cake.X:.2f} cakes")
else:
    print("No optimal solution found")

Ce code initialise le modèle, définit les variables et fixe l'objectif de profit. Il applique les contraintes que nous avons définies précédemment et détermine le plan optimal.

Comprendre les journaux du solveur

Lorsque vous exécutez model.optimize(), Gurobi génère un journal. Voici comment le lire :

Gurobi Optimizer version 13.0.0...
Presolve removed 0 rows and 0 columns
...
Explored 0 nodes (2 simplex iterations) in 0.01 seconds
Optimal objective  2.800000000e+02

• Pré-résolution: Gurobi simplifie votre problème avant de le résoudre. « Lignes supprimées » signifie que des contraintes redondantes ont été détectées.
• ItérationsSimplex: Le nombre d'étapes effectuées par l'algorithme. Des chiffres élevés pour des problèmes mineurs peuvent indiquer des problèmes de formulation.
• Objectifoptimal: Votre résultat final (par exemple, un bénéfice de 280 $).
• Écart: Pour les problèmes entiers, cela indique la différence entre la meilleure solution trouvée jusqu'à présent et la meilleure solution théorique.

En observant le journal, vous pouvez déterminer si un modèle est « bloqué » ou s'il fonctionne simplement de manière intensive.

Les concepts présentés ici sont directement proportionnels. Que vous ayez 10 variables ou 10 000, le modèle reste identique.

Types de problèmes avancés pris en charge par Gurobi

La programmation linéaire n'est qu'un point de départ. Gurobi gère les types complexes qui reflètent les nuances du monde réel, y compris les nouvelles fonctionnalités MINLP non convexes de la version 13.0.

Programmation linéaire en nombres entiers mixtes

Qu'est-ce qui le distingue ?

La programmation mixte en nombres entiers (MIP) permet aux variables d'être des nombres entiers. Il n'est pas possible de construire des usines de 0,7, il est donc nécessaire de trouver des solutions entières.

Applications concrètes

Emplacement de l'installation : Envisagez-vous d'ouvrir un entrepôt dans la ville A ? Oui (1) ou Non (0).

Planification de la production : La taille des lots doit souvent être un nombre entier.

Conception du réseau : Les décisions de routage sont généralement binaires. Le trafic passe par une liaison ou ne passe pas.

Exemple : emplacement des installations

import gurobipy as gp
from gurobipy import GRB

model = gp.Model("facility_location")

cities = ['CityA', 'CityB', 'CityC']
fixed_costs = {'CityA': 10000, 'CityB': 8000, 'CityC': 12000}

open_warehouse = model.addVars(cities, vtype=GRB.BINARY, name="open")

model.setObjective(
    gp.quicksum(fixed_costs[city] * open_warehouse[city] for city in cities),
    GRB.MINIMIZE
)

model.addConstr(gp.quicksum(open_warehouse[city] for city in cities) >= 2)

model.optimize()

print("Open warehouses in:")
for city in cities:
    if open_warehouse[city].X > 0.5:
        print(f"  {city}")

Ici, nous utilisons des variables binaires pour déterminer s'il convient d'ouvrir un entrepôt. Le modèle minimise les coûts fixes tout en garantissant qu'au moins deux établissements restent ouverts.

Programmation quadratique et non linéaire

Programmation quadratique (QP)

Lorsque votre objectif comprend des termes au carré ou des produits variables, vous avez un QP. L'optimisation de portefeuille est un exemple classique, car le risque (variance) est quadratique.

Programmation à contraintes quadratiques (QCP)

Les contraintes peuvent également être quadratiques. Veuillez considérer les problèmes impliquant des cercles ou des limites courbes.

Exemple : optimisation de portefeuille

import gurobipy as gp
from gurobipy import GRB
import numpy as np

model = gp.Model("portfolio")

assets = ['StockA', 'StockB', 'StockC']
expected_returns = [0.12, 0.18, 0.10]

covariance = np.array([
    [0.04, 0.01, 0.02],
    [0.01, 0.09, 0.03],
    [0.02, 0.03, 0.05]
])

weights = model.addVars(len(assets), name="weight", lb=0, ub=1)

model.setObjective(
    gp.quicksum(expected_returns[i] * weights[i] for i in range(len(assets))),
    GRB.MAXIMIZE
)

model.addConstr(gp.quicksum(weights[i] for i in range(len(assets))) == 1)

risk_expr = gp.quicksum(
    covariance[i][j] * weights[i] * weights[j]
    for i in range(len(assets))
    for j in range(len(assets))
)
model.addConstr(risk_expr <= 0.05, name="risk_limit")

model.optimize()

print("Optimal portfolio allocation:")
for i, asset in enumerate(assets):
    print(f"{asset}: {weights[i].X * 100:.1f}%")

Cette configuration traite de l'optimisation du portefeuille. Il maximise les rendements tout en limitant strictement le risque total (variance) à l'aide de contraintes quadratiques.

Types de problèmes supplémentaires pris en charge

Programmation conique du second ordre (SOCP)

Les problèmes impliquant des contraintes géométriques, tels que la définition d'un cône ou d'une limite circulaire, relèvent de cette catégorie. Courant dans l'optimisation robuste et la conception technique.

Programmation quadratique en nombres entiers mixtes (MIQP)

Combine des variables entières avec des objectifs ou des contraintes quadratiques. Utile dans l'optimisation discrète avec des relations non linéaires.

Gurobi prend en charge tous ces types de manière native. Il n'est pas nécessaire de reformuler les problèmes pour les adapter à un solveur spécifique, Gurobi détecte automatiquement le type de problème et applique les algorithmes appropriés.

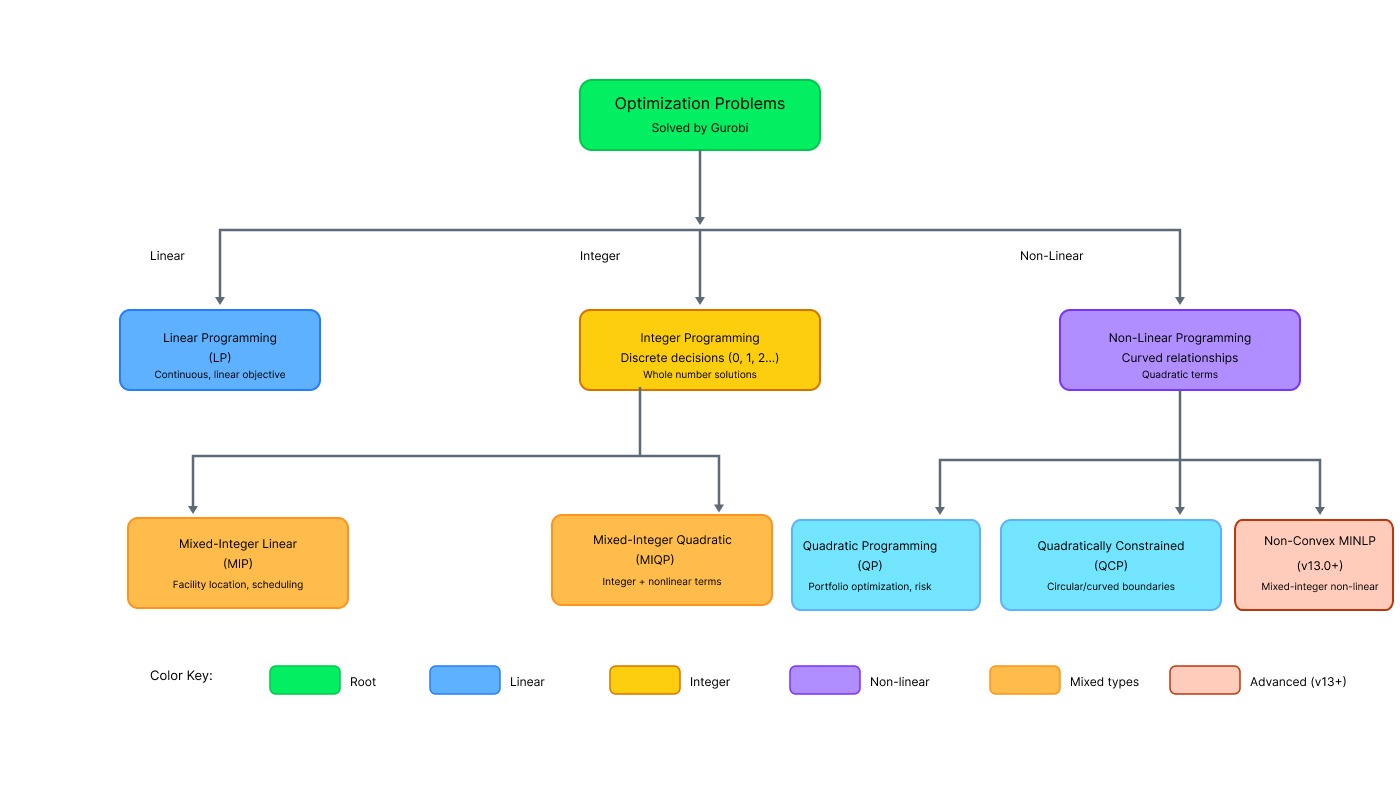
Types de problèmes d'optimisation pris en charge par Gurobi. Image fournie par l'auteur.

Algorithmes Gurobi et leurs applications

Sélection de l'algorithme

Gurobi sélectionne automatiquement les algorithmes, mais il est utile de connaître les options disponibles pour résoudre les problèmes de lenteur de résolution.

Valeurs de la méthode :

• -1 (par défaut) : Laissez Gurobi prendre la décision

• 0: Simplex primitif (convient à la plupart des LP)

• 1: Simplex double (efficace lorsque l'on part d'une situation irréalisable)

• 2: Barrière (idéale pour les modèles volumineux ou QP)

• 3: Concurrent (exécute plusieurs méthodes, sélectionne la plus rapide)

• 4: Concurrence déterministe

• 5: Simplexe concurrent déterministe

• PDHG (méthode du premier ordre : Gurobi 13.0 inclut également PDHG, une méthode basée sur les gradients, idéale pour les LP massifs qui s'adaptent aux GPU.

Veuillez vérifier lequel a été exécuté en consultant le journal du solveur (par exemple, « Modèle résolu avec barrière... »).

Quand remplacer: Si le défaut prend plusieurs heures, veuillez essayer Barrier pour les modèles volumineux ou Concurrent pour les problèmes imprévisibles.

model.Params.Method = 2
model.Params.BarConvTol = 1e-8

Cela sélectionne explicitement la méthode Barrière et réduit la tolérance, ce qui est utile lorsque l'on traite des ensembles de données volumineux ou sensibles.

Utilisation des fonctionnalités avancées de Gurobi

Une fois que vous maîtrisez les bases, Gurobi propose des outils performants pour résoudre des problèmes à l'échelle de l'entreprise.

Optimisation distribuée

Pour les modèles volumineux qui prennent trop de temps sur une seule machine, il est possible de répartir le travail. L'optimisation distribuée de Gurobi utilise plusieurs ordinateurs pour résoudre un seul problème plus rapidement.

Vous désignez une machine comme « gestionnaire » et les autres comme « travailleurs ». Le gestionnaire distribue des parties de l'arbre de recherche aux collaborateurs, qui les traitent en parallèle. Cela peut sembler excessif pour les modèles de petite taille, mais c'est essentiel pour les problèmes liés à la chaîne d'approvisionnement mondiale ou à la planification des horaires des compagnies aériennes.

Optimisation multi-objectifs

Dans la vie réelle, il est rare d'avoir un seul objectif. Vous pourriez souhaiter maximiser vos profits et minimiser votre impact environnemental.

Gurobi gère cela en vous permettant de définir des priorités. Vous pouvez lui indiquer de « maximiser d'abord les bénéfices, puis de minimiser le gaspillage sans réduire les bénéfices de plus de 10 % ». Vous pouvez également les pondérer : Objective = 0.7 * Profit - 0.3 * Waste.

# Multi-objective example
model.setObjectiveN(profit_expr, index=0, priority=2, name="Profit")
model.setObjectiveN(waste_expr, index=1, priority=1, name="Waste")

Interaction en temps réel et rappels

Il arrive parfois que vous souhaitiez intervenir pendant que Gurobi effectue ses calculs. Les rappels vous permettent d'exécuter du code personnalisé à des moments précis, par exemple chaque fois qu'une nouvelle solution est trouvée.

J'utilise des rappels pour interrompre prématurément le processus si une solution est « suffisamment satisfaisante » ou pour intégrer des heuristiques personnalisées dont je sais qu'elles fonctionnent pour mes données spécifiques.

Capacités du cloud

L'optimisation de votre ordinateur portable convient pour le développement, mais la production nécessite souvent davantage de puissance. Gurobi Cloud vous permet de transférer les tâches les plus lourdes vers AWS, Azure ou le cloud instantané de Gurobi. Vous ne payez que pour le temps de résolution, ce qui est idéal pour les charges de travail sporadiques et importantes.

Meilleures pratiques en matière de modélisation pratique

La rédaction de modèles efficaces nécessite une stratégie. Voici quelques conseils pour maintenir votre code propre et rapide.

Stratégies de formulation de modèles

Commencez par des éléments simples, puis ajoutez progressivement de la complexité.

Veuillez éviter de créer un modèle comportant 50 contraintes dès le premier jour. Commencez par la logique de base, vérifiez-la, puis affinez-la. J'ai consacré beaucoup de temps à déboguer des modèles complexes pour finalement découvrir que l'erreur se trouvait dans les éléments de base.

Utilisez des noms de variables et de contraintes significatifs.

x1 = model.addVar(name="x1")
model.addConstr(x1 + x2 <= 100, name="c1")

units_produced = model.addVar(name="units_produced")
model.addConstr(
    units_produced + units_stored <= warehouse_capacity,
    name="warehouse_capacity_limit"
)

Veuillez noter la différence : le deuxième bloc décrit clairement la logique métier. Comme je l'ai mentionné précédemment, cela vous évite des difficultés de débogage.

Pré-traiter les données

Veuillez vérifier vos données avant de procéder à la modélisation. Veuillez vérifier s'il existe des valeurs manquantes ou des contraintes irréalisables. Il est regrettable de détecter des erreurs dans les données après trois heures de résolution.

Adaptez vos données de manière appropriée

Gurobi gère efficacement la précision numérique, mais les valeurs extrêmes peuvent poser des difficultés. Si les coûts sont exprimés en millions et les quantités en millièmes, convertissez-les à des ordres de grandeur similaires :

# Instead of cost = 10000000 and quantity = 0.0001
# Scale to cost = 10 (in millions) and quantity = 100 (in 1/1000 units)

Les problèmes numériques sont rares dans les modèles bien dimensionnés, mais fréquents dans ceux qui le sont moins.

Considérations relatives à la stabilité numérique

Gurobi utilise l'arithmétique en virgule flottante, qui n'est pas infinie. Si votre contrainte indique « x <= 1000000000 » (Taille minimale de 1000) et que votre tolérance est « 1e-6 » (Taille maximale de 1000), vous pourriez obtenir des résultats inattendus.

Veuillez éviter les contraintes de type « Big M » telles que if y=0 then x <= 1,000,000,000. Veuillez plutôt sélectionner la plus petite limite supérieure valide (par exemple, la taille totale du marché). Des limites plus strictes permettent des résolutions plus rapides et plus stables.

Démarrages à chaud et modifications de modèles

Il est rare de résoudre un problème en une seule fois. En général, de nouvelles données sont disponibles (par exemple, une mise à jour de la demande).

Au lieu de reconstruire le modèle à partir de zéro, veuillez utiliser un démarrage à chaud. Veuillez fournir à Gurobi la solution précédente comme point de départ. Étant donné que le plan optimal d'hier est probablement similaire à celui d'aujourd'hui, Gurobi peut ignorer une grande partie du travail de recherche.

# Warm start example
bread.Start = 40  # Start search assuming we bake 40 loaves

Interfaces de programmation et intégration

API Python de Gurobi

Nous avons utilisé gurobipy car il est conforme à la philosophie Python. Il prend en charge la surcharge des opérateurs (x + y <= 5) et s'intègre directement à pandas et NumPy. Il s'agit de la méthode la plus courante pour utiliser Gurobi dans le domaine de la science des données.

Intégration avec d'autres langues

Les systèmes de production fonctionnent souvent sous C++, Java ou .NET pour des raisons de rapidité. Gurobi prend en charge l'ensemble de ces fonctionnalités. Les concepts (variables, contraintes, objectifs) sont identiques ; seule la syntaxe diffère.

Pour les flux de travail multilingues, je réalise souvent des prototypes en Python (codage rapide) et je les déploie en C++ (exécution rapide), en utilisant les formats de fichiers Gurobi (.mps ou .lp) pour transférer les modèles entre les deux.

Prise en charge du langage de modélisation

Gurobi s'intègre également à des langages de modélisation dédiés tels que AMPL et GAMS, ou même Excel.

- AMPL/GAMS : Idéal pour les chercheurs en mathématiques pures qui ne souhaitent pas écrire de code logiciel.

- Excel : Utile pour créer rapidement des prototypes ou présenter aux parties prenantes de l'entreprise un modèle qu'elles peuvent manipuler sans avoir à installer Python.

Optimisation et réglage des performances

Optimisation du flux de travail

Veuillez éviter de régler au hasard. Veuillez suivre cette procédure :

1. Mesurer l'de base: Veuillez exécuter avec les paramètres par défaut et noter le temps de résolution.

2. Définissez d'abord des limites strictes: Les systèmes de production nécessitent de l' TimeLimit.

3. Privilégiez la précision à la rapidité: Veuillez assouplir l' MIPGap e uniquement si les activités commerciales le permettent.

4. s relatives à la mise à l'échelle du fil de test: Un nombre plus élevé de threads n'implique pas nécessairement une augmentation de la vitesse (les gains diminuent après 4 à 8 threads).

# Example: Production deployment
model.Params.TimeLimit = 300  # Hard 5-min cutoff for API response
baseline_time = model.Runtime

if baseline_time > 240:  # If cutting it close
    model.Params.MIPGap = 0.02  # Accept 2% suboptimality
    # Business rationale: 2% cost increase < late delivery penalty

Critères de performance

Les tests de performance démontrent que Gurobi surpasse systématiquement les solveurs open source de plusieurs ordres de grandeur sur les problèmes MIP complexes. Bien qu'scipy s gère efficacement les petits LP, Gurobi excelle lorsque la complexité augmente. Vous trouverez des benchmarks comparatifs sur le site Web de Hans Mittelmann, qui évalue de manière indépendante les performances des solveurs.

Débogage et dépannage

Impossibilité du modèle

Lorsque Gurobi signale « Le modèle est irréalisable », cela signifie que vos contraintes sont en conflit. Aucune solution ne satisfait tous ces critères simultanément.

Identifiez les contraintes conflictuelles :

model.computeIIS()
model.write("infeasible.ilp")

print("Conflicting constraints:")
for c in model.getConstrs():
    if c.IISConstr:
        print(f"  {c.ConstrName}: {c.ConstrExpr}")

Ceci calcule le sous-système irréductible incohérent (IIS) et affiche précisément quelles contraintes sont en conflit les unes avec les autres.

Modèles non limités

Un modèle illimité signifie que l'objectif peut s'améliorer indéfiniment. Indique généralement des contraintes manquantes.

Veuillez vérifier :

- Avez-vous lié toutes les variables ? addVar(lb=0, ub=1000)

- Les contraintes sont-elles correctement formulées ?

- La fonction objectif est-elle correcte ?

Utilisation des journaux du solveur

Activez la journalisation détaillée pour observer le fonctionnement de Gurobi :

model.Params.OutputFlag = 1
model.Params.LogToConsole = 1
model.Params.LogFile = "gurobi.log"

Cela active la sortie détaillée et enregistre une copie dans un fichier local, vous fournissant ainsi un historique détaillé du processus de résolution.

Traitement des données

Dans les applications réelles, les données proviennent de fichiers et non de listes codées en dur.

import pandas as pd

# Load data
df = pd.read_csv("facility_costs.csv")
fixed_costs = dict(zip(df['city'], df['fixed_cost']))

# Validate BEFORE modeling
if any(c < 0 for c in fixed_costs.values()):
    raise ValueError("Costs cannot be negative")

Ce modèle, Load-Validate-Model, permet d'éviter les erreurs silencieuses.

Applications concrètes de Gurobi

La théorie est intéressante, mais examinons comment les industries l'utilisent concrètement.

Optimisation de la chaîne logistique

Conception du réseau de distribution

FedEx, UPS et Amazon appliquent les concepts du cours « Supply Chain Analytics in Python » (Analyse de la chaîne logistique en Python) afin de minimiser les coûts tout en respectant les garanties de livraison.

Nous utiliserons l'API Matrix pour cet exemple afin de gérer efficacement l'échelle.

import gurobipy as gp
from gurobipy import GRB
import numpy as np

# 1. Data Generation
factories = ["F1", "F2"]
warehouses = ["W1", "W2", "W3"]
customers = ["C1", "C2", "C3", "C4"]

# Cost matrices (Factory->Warehouse, Warehouse->Customer)
transport_fw = np.array([[2.0, 4.0, 5.0], [3.0, 1.0, 6.0]])
transport_wc = np.array([
    [1.5, 2.0, 3.0, 4.0],
    [3.0, 1.0, 2.0, 2.5],
    [5.0, 4.0, 1.0, 1.5]
])

# Capacity and Demand
factory_cap = np.array([1000, 1000])
demand = np.array([300, 500, 400, 600])

try:
    with gp.Model("SupplyChain_Matrix") as model:
        # 2. Variables (Matrix Form)
        # Flow F->W and W->C
        flow_fw = model.addMVar((len(factories), len(warehouses)), name="fw")
        flow_wc = model.addMVar((len(warehouses), len(customers)), name="wc")
        
        # Binary decision: Open warehouse?
        open_w = model.addMVar(len(warehouses), vtype=GRB.BINARY, name="open")

        # 3. Objective: Minimize Transport + Fixed Costs
        fixed_cost = 5000
        obj = (transport_fw * flow_fw).sum() + \
              (transport_wc * flow_wc).sum() + \
              (fixed_cost * open_w).sum()
        model.setObjective(obj, GRB.MINIMIZE)

        # 4. Constraints
        # Factory capacity (sum rows of flow_fw <= cap)
        model.addConstr(flow_fw.sum(axis=1) <= factory_cap, name="Cap")

        # Customer demand (sum cols of flow_wc >= demand)
        model.addConstr(flow_wc.sum(axis=0) >= demand, name="Demand")

        # Flow balance: Inflow to W == Outflow from W
        model.addConstr(flow_fw.sum(axis=0) == flow_wc.sum(axis=1), name="Balance")

        # Warehouse capacity linking: Flow out <= BigM * OpenBinary
        model.addConstr(flow_wc.sum(axis=1) <= 2000 * open_w, name="Link")

        model.optimize()

        if model.Status == GRB.OPTIMAL:
            print(f"Optimal Cost: ${model.ObjVal:,.2f}")
            print(f"Open Warehouses: {open_w.X}")

except gp.GurobiError as e:
    print(f"Error: {e}")

Cette approche vectorisée (addMVar, sum(axis=1)) traite instantanément des milliers de variables, évitant ainsi les boucles Python lentes.

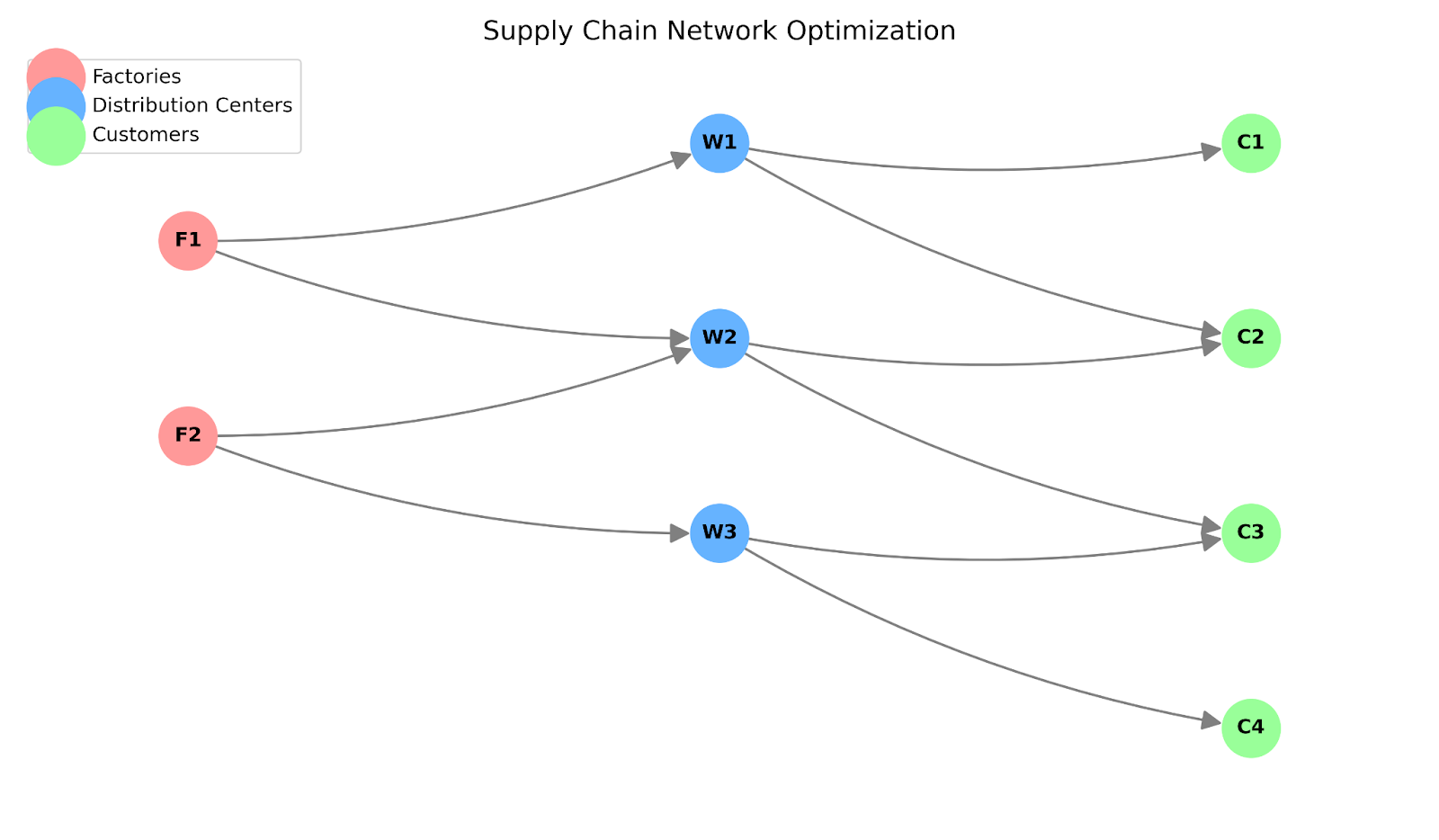
Graphique du réseau de la chaîne d'approvisionnement. Image fournie par l'auteur.

Optimisation des stocks

Il est délicat de trouver le juste équilibre entre les coûts liés aux commandes, au stockage et aux ruptures de stock. En raison de l'incertitude de la demande, cela devient une optimisation stochastique, que Gurobi gère via la modélisation de scénarios.

Planification des effectifs

Planification des quarts de travail

Les hôpitaux et les centres d'appels doivent planifier les horaires des employés tout en respectant les besoins en personnel, les règles du travail et les préférences.

Il s'agit de programmation mixte en nombres entiers. Chaque tâche est un choix binaire. Un hôpital comptant 100 infirmières et 50 équipes de travail doit gérer 5 000 variables.

Exemple : planification des horaires des infirmières

import gurobipy as gp
from gurobipy import GRB

model = gp.Model("nurse_scheduling")

nurses = ['Alice', 'Bob', 'Carol', 'Dave']
shifts = ['Mon_Day', 'Mon_Night', 'Tue_Day', 'Tue_Night']
min_required = {'Mon_Day': 2, 'Mon_Night': 1, 'Tue_Day': 2, 'Tue_Night': 1}

schedule = model.addVars(nurses, shifts, vtype=GRB.BINARY, name="schedule")

model.setObjective(
    gp.quicksum(schedule[n, s] for n in nurses for s in shifts),
    GRB.MINIMIZE
)

for shift in shifts:
    model.addConstr(
        gp.quicksum(schedule[n, shift] for n in nurses) >= min_required[shift],
        name=f"min_staff_{shift}"
    )

for nurse in nurses:
    model.addConstr(
        gp.quicksum(schedule[nurse, s] for s in shifts) <= 3,
        name=f"max_shifts_{nurse}"
    )

for nurse in nurses:
    # Labor rule: 8-hour rest required between shifts
    model.addConstr(
        schedule[nurse, 'Mon_Day'] + schedule[nurse, 'Mon_Night'] <= 1,
        name=f"no_double_{nurse}_Mon"
    )
    model.addConstr(
        schedule[nurse, 'Tue_Day'] + schedule[nurse, 'Tue_Night'] <= 1,
        name=f"no_double_{nurse}_Tue"
    )

model.optimize()

print("Optimal schedule:")
for nurse in nurses:
    assigned = [s for s in shifts if schedule[nurse, s].X > 0.5]
    print(f"{nurse}: {', '.join(assigned)}")

Ceci modélise le problème de planification à l'aide de variables binaires. Il minimise le nombre total de quarts de travail tout en respectant les besoins en personnel, le nombre maximal d'heures et les périodes de repos obligatoires.

Optimisation du portefeuille financier

Rapport risque-rendement

L'optimisation du portefeuille permet d'équilibrer les rendements attendus et les risques. Le modèle classique de Markowitz :

• Optimiser l': Rendement attendu
• Sous réserve de l': Risque (variance) inférieur au seuil
• s de contraintes: Contraintes budgétaires, exigences de diversification, limites réglementaires

Il s'agit de programmation quadratique. Le rendement est linéaire par rapport aux pondérations du portefeuille, mais la variance est quadratique (elle implique des produits de pondérations).

Considérations pratiques

L'optimisation réelle du portefeuille comprend :

• Frais de transaction (des frais s'appliquent à l'achat et à la vente)
• Contraintes sur les nombres entiers (il n'est pas possible d'acheter des fractions de certaines actions)
• Exigences réglementaires (ne peut dépasser 10 % dans un seul titre)
• Contraintes de rééquilibrage (ne pas modifier de manière trop radicale le portefeuille existant)

Les gestionnaires d'actifs effectuent ces optimisations quotidiennement, gérant des milliards de capitaux. Le temps de résolution du modèle a un impact direct sur l'exécution de la stratégie de trading.

Conclusion

Nous avons abordé de nombreux sujets, de l'installation de Gurobi à la création de modèles complexes de chaîne logistique.

Désormais, au lieu de débattre des opinions dans une salle de réunion, vous pouvez afficher le code à l'écran. Voici le plan mathématiquement optimal. Cela modifie la conversation. Vous cessez de deviner et commencez à prouver.

N'hésitez pas à l'essayer lors de votre prochain problème complexe, ce conflit d'horaires ou cette contrainte budgétaire que vous avez évité jusqu'à présent. Vous pourriez découvrir que la réponse parfaite se trouvait dans vos données depuis le début.

Si vous souhaitez approfondir vos compétences en optimisation, nous vous invitons à consulter nos cours « Introduction à la programmation linéaire » et « Introduction à l'optimisation en Python » pour continuer à vous perfectionner.