Gurobi: Optimización matemática para problemas complejos

Los solucionadores básicos y los métodos de prueba y error tienen dificultades cuando las variables aumentan de escala. Gurobi maneja estas complejidades con rapidez y precisión, resolviendo en segundos problemas que, de otro modo, podrían llevar horas. Esa es la diferencia entre esperar un plan viable y demostrar matemáticamente que tienes el óptimo.

Este tutorial te guíaa través del potente solucionador comercial conocido como Gurobi . Te mostraré cómo instalar la biblioteca Python, formular tu primer modelo y pasar a problemas más avanzados, como la programación mixta entera.

Comprender la optimización matemática y el papel de Gurobi

Antes de escribir código, es útil comprender qué significa realmente la optimización. Este contexto muestra cuándo utilizar Gurobi en lugar de los enfoques de programación estándar.

¿Qué es la optimización matemática?

La optimización matemática encuentra la mejor solución entre todas las soluciones posibles. Tú defines lo que significa «óptimo» (minimizar costes, maximizar beneficios, minimizar tiempo), lo que controlas (variables de decisión) y las limitaciones a las que te enfrentas (restricciones). El optimizador busca entre las soluciones viables para encontrar la óptima.

Esto difiere de la programación tradicional, en la que se especifican los pasos exactos. Con la optimización, describes el problema matemáticamente y dejas que el solucionador averigüe cómo resolverlo. No estás escribiendo una lógica «si esto, entonces aquello», sino que estás definiendo relaciones y dejando que los algoritmos encuentren los mejores valores.

La importancia de Gurobi en la optimización

Por qué Gurobi destaca

Gurobi se clasifica constantemente como uno de los optimizadores comerciales más rápidos disponibles. Las pruebas comparativas suelen mostrar que supera significativamente a las alternativas de código abierto en problemas a gran escala. Esta velocidad es importante cuando se ejecuta la optimización cada hora o se necesitan resultados dentro de plazos estrictos.

Adopción por parte de la industria

Empresas de los sectores de logística, finanzas, energía y salud utilizan Gurobi para sus sistemas de producción. FedEx optimiza las rutas de entrega, mientras que las empresas financieras asignan miles de millones en portafolios. Las empresas energéticas programan la generación de energía. No se trata de ejercicios académicos, sino de sistemas que manejan dinero real y restricciones reales.

Capacidades del solucionador

Gurobi maneja programación lineal (LP), programación mixta entera (MIP), programación cuadrática (QP) y mucho más. Incluye algoritmos de última generación, como la optimización concurrente, en la que se ejecutan varios métodos de solución en paralelo y gana el más rápido. Obtienes fiabilidad y velocidad sin tener que elegir algoritmos manualmente.

Configuración de Gurobi

La instalación de Gurobi se realiza en unos pocos pasos. Una vez configurado, funciona a la perfección con Python.

Instalación y configuración

Descargar e instalar

Veal sitio web de Gurobi y descarga el instalador para tu sistema operativo. Incluye el optimizador, la interfaz gurobipy y la documentación. Ejecuta el instaladorcon la configuración predeterminada, a menos que necesites una ruta personalizada.

Después de la instalación, comprueba que funciona:

import gurobipy as gp
print(f"Gurobi version: {gp.__version__}")

Aquí verificamos la instalación imprimiendo el número de versión. Una impresión satisfactoria confirma que tu entorno está listo.

Opciones de licencia

Gurobi requiere una licencia para cualquier cosa que vaya más allá de pequeños problemas de prueba. Tus opciones:

• Licencia de prueba gratuita: Evaluación de 30 días. Solicítalo en el sitio web de Gurobi con tu correo electrónico del trabajo.
• Licencia académica: Gratis para profesores y estudiantes. Verifica tu correo electrónico académico para obtener acceso ilimitado, ideal para el aprendizaje.
• Licencia comercial: Necesario para los negocios. Los precios varían según la escala. Las licencias para usuarios designados son adecuadas para científicos de datos individuales, mientras que las licencias flotantes permiten a los equipos compartir capacidad.
• Licencia en la nube: Pago por uso. Sin costes iniciales, solo pagas por lo que utilizas. Útil para tareas de optimización ocasionales.

Utilizo la licencia académica para el aprendizaje y la comercial para la producción. La prueba te da mucho tiempo para explorar antes de comprometerte.

Configuración del entorno

Configuración de Python

Gurobi funciona con Python 3.7+. Recomiendo utilizar un entorno virtual para evitar conflictos:

python -m venv gurobi_env
gurobi_env\Scripts\activate
source gurobi_env/bin/activate
pip install gurobipy

Estos comandos configuran un espacio de trabajo limpio e importan la biblioteca.

Integración con Jupyter Notebook

Para el desarrollo interactivo, los cuadernos funcionan muy bien con Gurobi:

pip install jupyter
jupyter notebook
import gurobipy as gp
print("Gurobi ready!")

Este fragmento instala Jupyter, inicia el servidor y ejecuta una comprobación rápida para garantizar que Gurobi se carga correctamente en el cuaderno.

Cuándo NO utilizar Gurobi

Gurobi es potente, pero no siempre es la opción adecuada.

• Problemas sencillos: Si tienes 50 variables y restricciones lineales básicas, los solucionadores gratuitos como scipy.optimize.linprog o Excel Solverfuncionan bien.

• Cost: Las licencias comerciales son caras. Para herramientas internas no críticas, pueden ser suficientes opciones de código abierto como CBC o GLPK (a través de PuLP).

• Heurística: Si necesitas una respuesta «suficientemente buena» en milisegundos para un juego en tiempo real, los métodos heurísticos (como los algoritmos genéticos) suelen superar a los solucionadores exactos.

Utiliza Gurobi cuando los problemas sean grandes (más de 10 000 variables) o necesites funciones avanzadas como restricciones cuadráticas.

Compatibilidad con plataformas

Gurobi funciona en Windows, macOS y Linux. Las nubes como AWS, Azure y Google Cloud son compatibles con Gurobi a través de sus mercados. He implementado modelos Gurobi en las tres principales nubes sin problemas específicos de la plataforma.

Modelos de optimización de edificios

Una vez instalado Gurobi, vamos a crear tu primer modelo. Estos conceptos básicos se aplican a todos los problemas que resolverás.

Componentes clave de un modelo de optimización

Cada modelo tiene tres partes esenciales:

Variables de decisión

Estas son las decisiones que toma el optimizador. En la planificación de la producción, esto podría ser «unidades del producto A» y «unidades del producto B». Tú defines las variables; Gurobi asigna los valores.

Función objetivo

Este es tu objetivo, lo que deseas maximizar o minimizar. Maximizar los beneficios (3*product_a + 5*product_b) o minimizar los costes. Tú obtienes un objetivo por modelo.

Restricciones

Estos son tus límites. No puedes producir más de la capacidad de la fábrica ni gastar más de lo que permite tu presupuesto. Las restricciones definen qué soluciones son realmente posibles.

Mejores prácticas de formulación

Utiliza nombres de variables claros. En lugar de x[1], utiliza produce_product_a. Te ahorrará horas de depuración más adelante, como explicaré en la sección de resolución de problemas.

Mantén las restricciones sencillas. Dividir la lógica compleja en restricciones más pequeñas y sencillas hace que tu modelo sea más fácil de leer y depurar.

Modern Gurobi: La API de Matrix

Si tienes experiencia en ciencia de datos, es posible que el modelado basado en bucles te resulte lento. Gurobi 13.0+ ofrece una API Matrix que utiliza arreglos NumPy, lo que agiliza la creación de modelos entre 10 y 50 veces.

Así es como se ve un modelo de panadería utilizando vectores:

import gurobipy as gp
import numpy as np

# Data
prices = np.array([2.0, 5.0])
resources = np.array([[0.5, 2.0], [1.0, 1.0]])
limits = np.array([100.0, 80.0])

model = gp.Model("bakery_matrix")
x = model.addMVar(shape=2, name="x")

model.setObjective(prices @ x, gp.GRB.MAXIMIZE)
model.addConstr(resources @ x <= limits, name="constraints")

model.optimize()

Esta sintaxis A @ x <= b es más clara y estándar para los sistemas de producción.

Creación de un modelo sencillo de programación lineal

Resolvamos un problema práctico: una panadería decide cuántas barras de pan y pasteles hornear para maximizar los beneficios.

Planteamiento del problema:

- Beneficio del pan: 2 $ | Harina: 0,5 kg

- Beneficio del pastel: 5 $ | Harina: 2 kg

- Harina disponible: 100 kg

- Capacidad del horno: 80 artículos

Este es el modelo:

import gurobipy as gp
from gurobipy import GRB

model = gp.Model("bakery_optimization")

bread = model.addVar(name="bread", vtype=GRB.CONTINUOUS, lb=0)
cake = model.addVar(name="cake", vtype=GRB.CONTINUOUS, lb=0)

model.setObjective(2 * bread + 5 * cake, GRB.MAXIMIZE)

model.addConstr(0.5 * bread + 2 * cake <= 100, name="flour_limit")
model.addConstr(bread + cake <= 80, name="oven_capacity")

model.optimize()

if model.status == GRB.OPTIMAL:
    print(f"Optimal profit: ${model.objVal:.2f}")
    print(f"Bake {bread.X:.2f} loaves of bread")
    print(f"Bake {cake.X:.2f} cakes")
else:
    print("No optimal solution found")

Este código inicializa el modelo, define variables y establece el objetivo de beneficio. Aplica las restricciones que hemos definido anteriormente y resuelve el plan óptimo.

Comprender los registros del solucionador

Cuando ejecutas model.optimize(), Gurobi imprime un registro. A continuación te explicamos cómo leerlo:

Gurobi Optimizer version 13.0.0...
Presolve removed 0 rows and 0 columns
...
Explored 0 nodes (2 simplex iterations) in 0.01 seconds
Optimal objective  2.800000000e+02

• Resolución previa: Gurobi simplifica tu problema antes de resolverlo. «Filas eliminadas» significa que se han encontrado restricciones redundantes.
• Iteracionessimplex: Cuántos pasos dio el algoritmo. Un número elevado de pequeños problemas podría indicar problemas de formulación.
• Objetivoóptimo: Tu resultado final (por ejemplo, 280 $ de beneficio).
• Diferencia: Para problemas enteros, esto muestra la diferencia entre la mejor solución encontrada hasta ahora y la mejor solución teórica.

Observar el registro te ayuda a detectar si un modelo está «atascado» o simplemente trabajando intensamente.

Los conceptos aquí se aplican directamente. Tanto si tienes 10 variables como 10 000, el patrón sigue siendo el mismo.

Tipos de problemas avanzados compatibles con Gurobi

La programación lineal es solo el comienzo. Gurobi maneja tipos complejos que capturan los matices del mundo real, incluidas las nuevas capacidades MINLP no convexas de la versión 13.0.

Programación lineal mixta entera

¿Qué lo hace diferente?

La programación mixta entera (MIP) permite que las variables sean números enteros. No puedes construir fábricas de 0,7, por lo que necesitas soluciones enteras.

Aplicaciones en el mundo real

Ubicación de las instalaciones: ¿Abrir un almacén en la ciudad A? Sí (1) o No (0).

Programación de la producción: Los tamaños de los lotes a menudo deben ser números enteros.

Diseño de red: Las decisiones de enrutamiento suelen ser binarias. El tráfico fluye a través de un enlace o no fluye.

Ejemplo: ubicación de las instalaciones

import gurobipy as gp
from gurobipy import GRB

model = gp.Model("facility_location")

cities = ['CityA', 'CityB', 'CityC']
fixed_costs = {'CityA': 10000, 'CityB': 8000, 'CityC': 12000}

open_warehouse = model.addVars(cities, vtype=GRB.BINARY, name="open")

model.setObjective(
    gp.quicksum(fixed_costs[city] * open_warehouse[city] for city in cities),
    GRB.MINIMIZE
)

model.addConstr(gp.quicksum(open_warehouse[city] for city in cities) >= 2)

model.optimize()

print("Open warehouses in:")
for city in cities:
    if open_warehouse[city].X > 0.5:
        print(f"  {city}")

Aquí utilizamos variables binarias para decidir si abrir un almacén. El modelo minimiza los costes fijos y garantiza que al menos dos instalaciones permanezcan abiertas.

Programación cuadrática y no lineal

Programación cuadrática (QP)

Cuando tu objetivo incluye términos al cuadrado o productos variables, tienes un QP. La optimización de portafolios es un ejemplo clásico, ya que el riesgo (varianza) es cuadrático.

Programación con restricciones cuadráticas (QCP)

Las restricciones también pueden ser cuadráticas. Piensa en problemas relacionados con círculos o límites curvos.

Ejemplo: optimización de portafolio

import gurobipy as gp
from gurobipy import GRB
import numpy as np

model = gp.Model("portfolio")

assets = ['StockA', 'StockB', 'StockC']
expected_returns = [0.12, 0.18, 0.10]

covariance = np.array([
    [0.04, 0.01, 0.02],
    [0.01, 0.09, 0.03],
    [0.02, 0.03, 0.05]
])

weights = model.addVars(len(assets), name="weight", lb=0, ub=1)

model.setObjective(
    gp.quicksum(expected_returns[i] * weights[i] for i in range(len(assets))),
    GRB.MAXIMIZE
)

model.addConstr(gp.quicksum(weights[i] for i in range(len(assets))) == 1)

risk_expr = gp.quicksum(
    covariance[i][j] * weights[i] * weights[j]
    for i in range(len(assets))
    for j in range(len(assets))
)
model.addConstr(risk_expr <= 0.05, name="risk_limit")

model.optimize()

print("Optimal portfolio allocation:")
for i, asset in enumerate(assets):
    print(f"{asset}: {weights[i].X * 100:.1f}%")

Esta configuración aborda la optimización del portafolio. Maximiza los rendimientos al tiempo que limita estrictamente el riesgo total (varianza) mediante restricciones cuadráticas.

Tipos de problemas adicionales compatibles

Programación cónica de segundo orden (SOCP)

Los problemas que implican restricciones geométricas, como definir un cono o un límite circular, entran en esta categoría. Común en la optimización robusta y el diseño de ingeniería.

Programación cuadrática mixta entera (MIQP)

Combina variables enteras con objetivos o restricciones cuadráticas. Útil en la optimización discreta con relaciones no lineales.

Gurobi admite todos estos tipos de forma nativa. No es necesario reformular los problemas para adaptarlos a un solucionador específico, ya que Gurobi detecta automáticamente el tipo de problema y aplica los algoritmos adecuados.

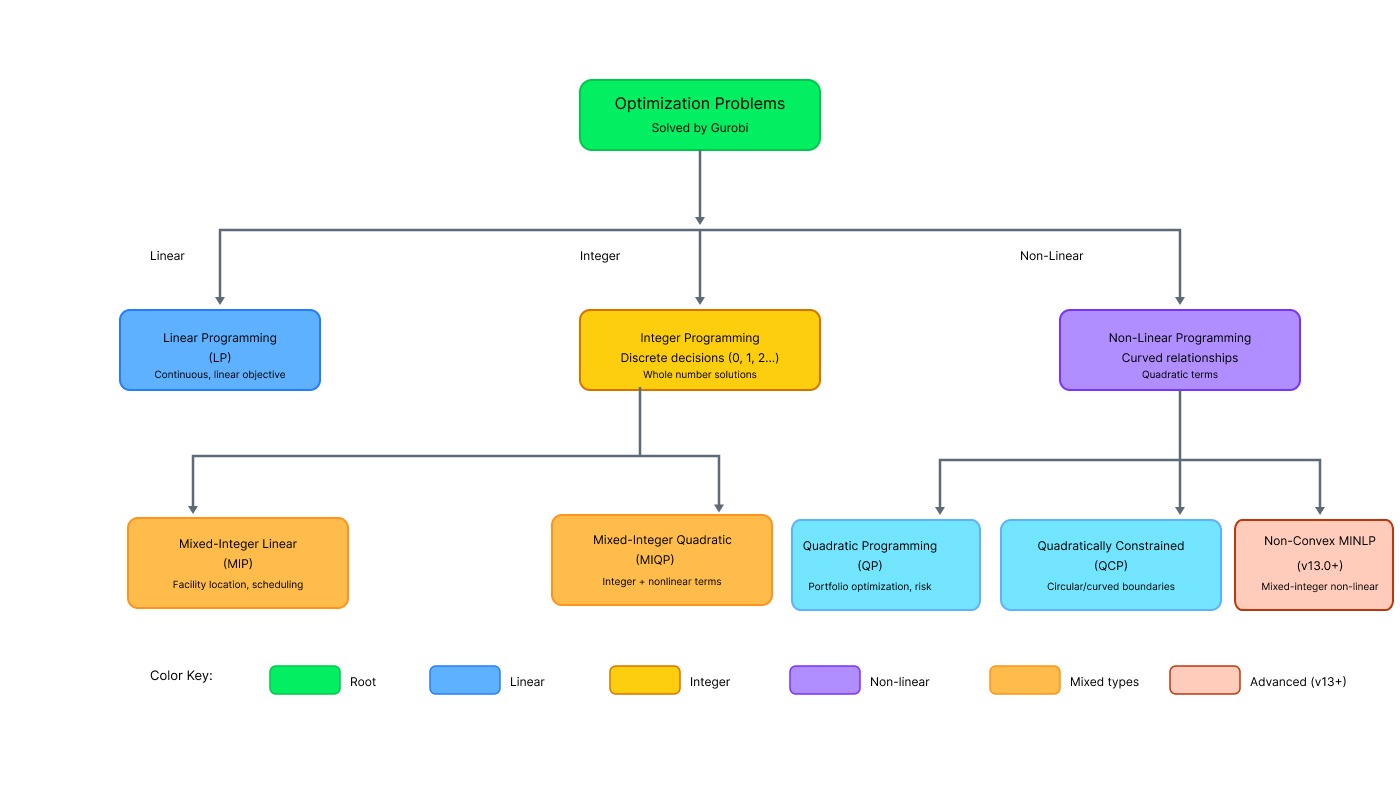
Tipos de problemas de optimización compatibles con Gurobi. Imagen del autor.

Los algoritmos de Gurobi y sus aplicaciones

Selección del algoritmo

Gurobi selecciona los algoritmos automáticamente, pero conocer las opciones ayuda a resolver los problemas de lentitud en la resolución.

Valores del método:

• -1 (predeterminado): Deja que Gurobi decida

• 0: Simplex primario (adecuado para la mayoría de LP)

• 1: Simplex dual (útil cuando se parte de una situación inviable)

• 2: Barrera (ideal para modelos masivos o QP)

• 3: Concurrente (ejecuta varios métodos y elige el más rápido)

• 4: Concurrente determinista

• 5: Simplex concurrente determinista

• PDHG (método de primer orden: Gurobi 13.0 también incluye PDHG, un método basado en gradientes ideal para LP masivos que se adapta a las GPU.

Comprueba cuál se ha ejecutado consultando el registro del solucionador (por ejemplo, «Modelo de barrera resuelto...»).

Cuándo anular: Si el valor predeterminado tarda horas, prueba Barrier para modelos grandes o Concurrent para problemas impredecibles.

model.Params.Method = 2
model.Params.BarConvTol = 1e-8

Esto selecciona explícitamente el método Barrera y reduce la tolerancia, lo que resulta útil cuando se trabaja con conjuntos de datos masivos o sensibles.

Uso de las funciones avanzadas de Gurobi

Una vez que domines los conceptos básicos, Gurobi te ofrece potentes herramientas para resolver problemas a escala empresarial.

Optimización distribuida

Para modelos muy grandes que tardan demasiado tiempo en procesarse en una sola máquina, puedes dividir el trabajo. La optimización distribuida de Gurobi utiliza varios ordenadores para resolver un único problema más rápidamente.

Se designa una máquina como «gestora» y las demás como «trabajadoras». El administrador envía partes del árbol de búsqueda a los trabajadores, quienes las resuelven en paralelo. Esto es excesivo para modelos pequeños, pero esencial para problemas relacionados con la cadena de suministro global o la programación de líneas aéreas.

Optimización multiobjetivo

En la vida real, rara vez hay un único objetivo. Es posible que quieras maximizar los beneficios y minimizar el impacto medioambiental.

Gurobi gestiona esto permitiéndote establecer prioridades. Puedes indicarle que «maximice primero los beneficios y luego minimice los residuos sin reducir los beneficios en más de un 10 %». Como alternativa, puedes ponderarlos: Objective = 0.7 * Profit - 0.3 * Waste.

# Multi-objective example
model.setObjectiveN(profit_expr, index=0, priority=2, name="Profit")
model.setObjectiveN(waste_expr, index=1, priority=1, name="Waste")

Interacción en tiempo real y devoluciones de llamada

A veces es posible que quieras intervenir mientras Gurobi está resolviendo. Las devoluciones de llamada te permiten ejecutar código personalizado en momentos específicos, como cada vez que se encuentra una nueva solución.

Utilizo callbacks para detenerme antes de tiempo si una solución es «suficientemente buena» o para introducir heurísticas personalizadas que sé que funcionan con tus datos específicos.

Capacidades de la nube

Ejecutar la optimización en tu ordenador portátil está bien para el desarrollo, pero la producción a menudo requiere más potencia. Gurobi Cloud te permite descargar el trabajo pesado a AWS, Azure o la propia Instant Cloud de Gurobi. Solo pagas por el tiempo de resolución, lo que resulta perfecto para cargas de trabajo esporádicas y pesadas.

Mejores prácticas de modelado práctico

Escribir modelos eficientes requiere una estrategia. Aquí tienes algunos consejos para mantener tu código limpio y rápido.

Estrategias de formulación de modelos

Empieza por lo sencillo y ve añadiendo complejidad poco a poco.

No construyas un modelo con 50 restricciones el primer día. Comienza con la lógica central, verifícala y luego perfecciónala. He dedicado demasiado tiempo a depurar modelos complejos solo para descubrir que el error estaba en lo básico.

Utiliza nombres significativos para las variables y las restricciones.

x1 = model.addVar(name="x1")
model.addConstr(x1 + x2 <= 100, name="c1")

units_produced = model.addVar(name="units_produced")
model.addConstr(
    units_produced + units_stored <= warehouse_capacity,
    name="warehouse_capacity_limit"
)

Observa la diferencia: el segundo bloque describe claramente la lógica empresarial. Como mencioné anteriormente, esto te ahorra dolores de cabeza a la hora de depurar.

Preprocesar datos

Valida tus datos antes de crear el modelo. Comprueba si hay valores que faltan o restricciones imposibles. Encontrar errores en los datos después de tres horas de trabajo es muy molesto.

Escala tus datos adecuadamente.

Gurobi maneja bien la precisión numérica, pero los valores extremos causan problemas. Si los costes se expresan en millones y las cantidades en milésimas, escaladlos a magnitudes similares:

# Instead of cost = 10000000 and quantity = 0.0001
# Scale to cost = 10 (in millions) and quantity = 100 (in 1/1000 units)

Los problemas numéricos son poco frecuentes en los modelos bien escalados, pero comunes en los mal escalados.

Consideraciones sobre la estabilidad numérica

Gurobi utiliza aritmética de coma flotante, que no es infinita. Si la restricción indica « x <= 1000000000 » y la tolerancia es «1e-6 », es posible que obtengas resultados extraños.

Evita restricciones como « if y=0 then x <= 1,000,000,000» (el problema del gran M) . En su lugar, elige el límite superior válido más pequeño (por ejemplo, el tamaño total del mercado). Los límites más estrictos permiten resoluciones más rápidas y estables.

Arranques en caliente y modificaciones del modelo

Rara vez se resuelve un problema con una sola vez. Por lo general, llegan nuevos datos (por ejemplo, demanda actualizada).

En lugar de reconstruir el modelo desde cero, utiliza un inicio en caliente. Le proporcionas a Gurobi la solución anterior como punto de partida. Dado que el plan óptimo de ayer probablemente sea similar al de hoy, Gurobi puede omitir gran parte del trabajo de búsqueda.

# Warm start example
bread.Start = 40  # Start search assuming we bake 40 loaves

Interfaces de programación e integración

API de Python de Gurobi

Hemos utilizado gurobipy porque es Pythonic. Admite la sobrecarga de operadores (x + y <= 5) y se integra directamente con pandas y NumPy. Es la forma más popular de utilizar Gurobi para la ciencia de datos.

Integración con otros idiomas

Los sistemas de producción suelen funcionar con C++, Java o .NET para ganar velocidad. Gurobi es compatible con todos ellos. Los conceptos (variables, restricciones, objetivos) son idénticos; solo cambia la sintaxis.

Para flujos de trabajo entre lenguajes, suelo crear prototipos en Python (codificación rápida) e implementar en C++ (ejecución rápida), utilizando los formatos de archivo de Gurobi (.mps o .lp) para transferir modelos entre ellos.

Compatibilidad con lenguajes de modelado

Gurobi también se conecta a lenguajes de modelado específicos como AMPL y GAMS, o incluso Excel.

- AMPL/GAMS: Ideal para investigadores puramente matemáticos que no desean escribir código de software.

- Excel: Útil para crear prototipos rápidos o mostrar a las partes interesadas del negocio un modelo que pueden tocar sin necesidad de instalar Python.

Optimización y ajuste del rendimiento

Ajuste del flujo de trabajo

No sintonices al azar. Sigue este proceso:

1. Medida de referencia: Ejecuta con los valores predeterminados y toma nota del tiempo de resolución.

2. Establece primero límites estrictos: Los sistemas de producción necesitan TimeLimit.

3. Precisión comercial por velocidad: Solo relaja MIPGap si el negocio lo tolera.

4. Prueba de escalado de subprocesos: Más subprocesos ≠ más rápido (rendimiento decreciente después de 4-8).

# Example: Production deployment
model.Params.TimeLimit = 300  # Hard 5-min cutoff for API response
baseline_time = model.Runtime

if baseline_time > 240:  # If cutting it close
    model.Params.MIPGap = 0.02  # Accept 2% suboptimality
    # Business rationale: 2% cost increase < late delivery penalty

Puntos de referencia de rendimiento

Las pruebas comparativas demuestran que Gurobi supera constantemente a los solucionadores de código abierto en varios órdenes de magnitud en problemas MIP difíciles. Aunque scipy funciona bien con LP pequeños, Gurobi destaca cuando la complejidad aumenta. Puedes encontrar comparativas en la página web de Hans Mittelmann, que realiza un seguimiento independiente del rendimiento de los solucionadores.

Depuración y resolución de problemas

Inviabilidad del modelo

Cuando Gurobi informa «El modelo no es viable», tus restricciones entran en conflicto. Ninguna solución satisface a todos vosotros al mismo tiempo.

Encuentra las restricciones conflictivas:

model.computeIIS()
model.write("infeasible.ilp")

print("Conflicting constraints:")
for c in model.getConstrs():
    if c.IISConstr:
        print(f"  {c.ConstrName}: {c.ConstrExpr}")

Esto calcula el subsistema inconsistente irreducible (IIS) e imprime exactamente qué restricciones entran en conflicto entre sí.

Modelos sin límites

Un modelo sin límites significa que el objetivo puede mejorar infinitamente. Normalmente indica restricciones faltantes.

Comprueba:

- ¿Has vinculado todas las variables? addVar(lb=0, ub=1000)

- ¿Están correctamente formuladas las restricciones?

- ¿Es correcta la función objetivo?

Uso de registros del solucionador

Habilita el registro detallado para ver qué está haciendo Gurobi:

model.Params.OutputFlag = 1
model.Params.LogToConsole = 1
model.Params.LogFile = "gurobi.log"

Esto habilita la salida detallada y guarda una copia en un archivo local, lo que te proporciona un historial detallado del proceso de resolución.

Manejo de datos

En las aplicaciones reales, los datos proceden de archivos, no de listas codificadas.

import pandas as pd

# Load data
df = pd.read_csv("facility_costs.csv")
fixed_costs = dict(zip(df['city'], df['fixed_cost']))

# Validate BEFORE modeling
if any(c < 0 for c in fixed_costs.values()):
    raise ValueError("Costs cannot be negative")

Este patrón, Load-Validate-Model, evita los errores silenciosos.

Aplicaciones reales de Gurobi

La teoría está muy bien, pero veamos cómo lo utilizan realmente las industrias.

Optimización de la cadena de suministro

Diseño de la red de distribución

FedEx, UPS y Amazon utilizan los conceptos del curso «Análisis de la cadena de suministro en Python» para minimizar los costes y cumplir al mismo tiempo las garantías de entrega.

Usaremos la API Matrix para este ejemplo con el fin de gestionar la escala de manera eficiente.

import gurobipy as gp
from gurobipy import GRB
import numpy as np

# 1. Data Generation
factories = ["F1", "F2"]
warehouses = ["W1", "W2", "W3"]
customers = ["C1", "C2", "C3", "C4"]

# Cost matrices (Factory->Warehouse, Warehouse->Customer)
transport_fw = np.array([[2.0, 4.0, 5.0], [3.0, 1.0, 6.0]])
transport_wc = np.array([
    [1.5, 2.0, 3.0, 4.0],
    [3.0, 1.0, 2.0, 2.5],
    [5.0, 4.0, 1.0, 1.5]
])

# Capacity and Demand
factory_cap = np.array([1000, 1000])
demand = np.array([300, 500, 400, 600])

try:
    with gp.Model("SupplyChain_Matrix") as model:
        # 2. Variables (Matrix Form)
        # Flow F->W and W->C
        flow_fw = model.addMVar((len(factories), len(warehouses)), name="fw")
        flow_wc = model.addMVar((len(warehouses), len(customers)), name="wc")
        
        # Binary decision: Open warehouse?
        open_w = model.addMVar(len(warehouses), vtype=GRB.BINARY, name="open")

        # 3. Objective: Minimize Transport + Fixed Costs
        fixed_cost = 5000
        obj = (transport_fw * flow_fw).sum() + \
              (transport_wc * flow_wc).sum() + \
              (fixed_cost * open_w).sum()
        model.setObjective(obj, GRB.MINIMIZE)

        # 4. Constraints
        # Factory capacity (sum rows of flow_fw <= cap)
        model.addConstr(flow_fw.sum(axis=1) <= factory_cap, name="Cap")

        # Customer demand (sum cols of flow_wc >= demand)
        model.addConstr(flow_wc.sum(axis=0) >= demand, name="Demand")

        # Flow balance: Inflow to W == Outflow from W
        model.addConstr(flow_fw.sum(axis=0) == flow_wc.sum(axis=1), name="Balance")

        # Warehouse capacity linking: Flow out <= BigM * OpenBinary
        model.addConstr(flow_wc.sum(axis=1) <= 2000 * open_w, name="Link")

        model.optimize()

        if model.Status == GRB.OPTIMAL:
            print(f"Optimal Cost: ${model.ObjVal:,.2f}")
            print(f"Open Warehouses: {open_w.X}")

except gp.GurobiError as e:
    print(f"Error: {e}")

Este enfoque vectorizado (addMVar, sum(axis=1)) maneja miles de variables al instante, evitando los lentos bucles de Python.

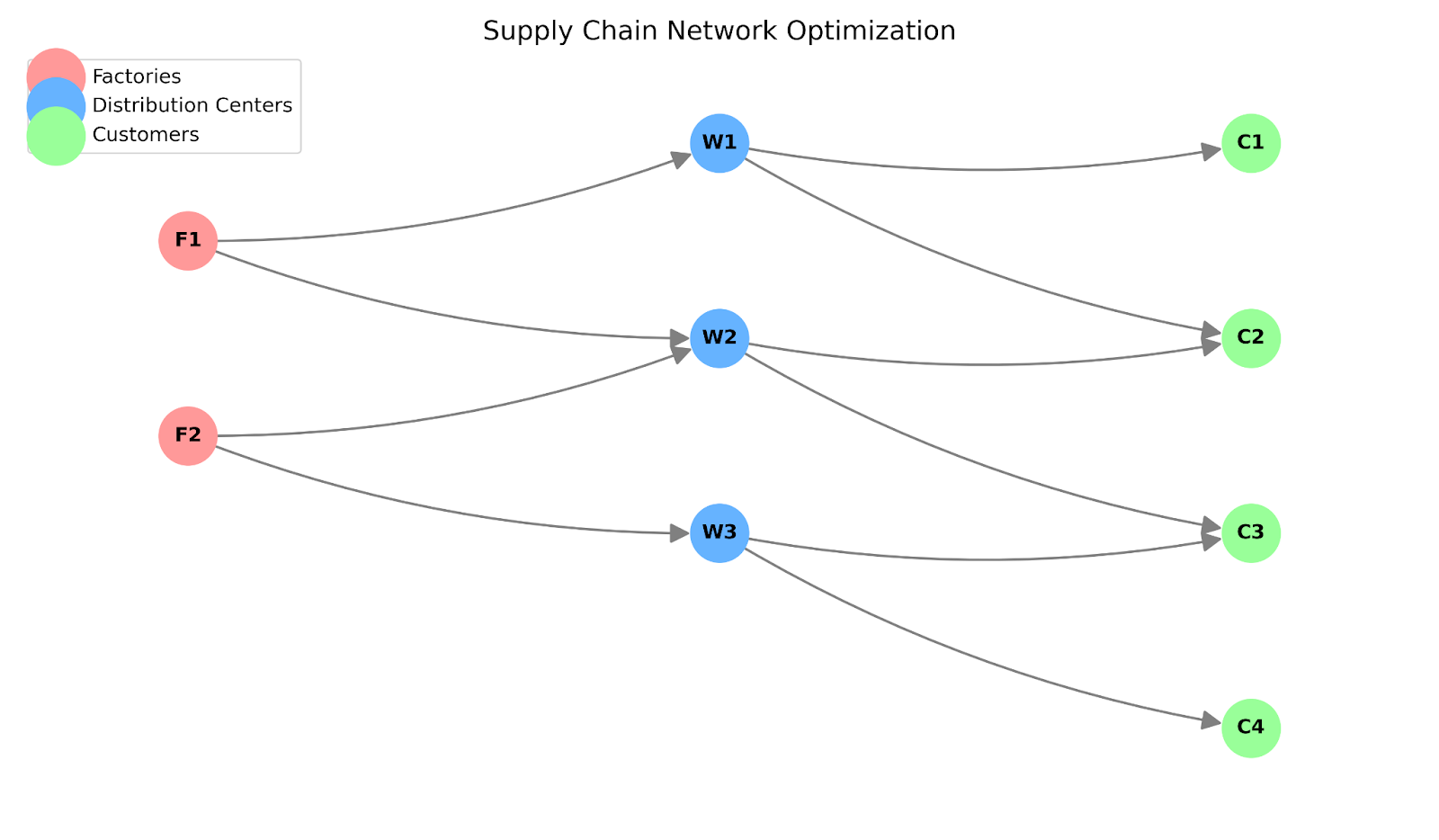
Gráfico de la red de la cadena de suministro. Imagen del autor.

Optimización del inventario

Equilibrar los costes de los pedidos, el almacenamiento y la escasez es complicado. Con una demanda incierta, esto se convierte en una optimización estocástica, que Gurobi gestiona mediante el modelado de escenarios.

Programación de la plantilla

Planificación de turnos

Los hospitales y los centros de atención telefónica deben programar los horarios de los trabajadores respetando las necesidades de personal, las normas laborales y las preferencias.

Esto es programación mixta entera pura. Cada tarea es una elección binaria. Un hospital con 100 enfermeras y 50 turnos tiene 5000 variables con las que lidiar.

Ejemplo: programación de enfermeras

import gurobipy as gp
from gurobipy import GRB

model = gp.Model("nurse_scheduling")

nurses = ['Alice', 'Bob', 'Carol', 'Dave']
shifts = ['Mon_Day', 'Mon_Night', 'Tue_Day', 'Tue_Night']
min_required = {'Mon_Day': 2, 'Mon_Night': 1, 'Tue_Day': 2, 'Tue_Night': 1}

schedule = model.addVars(nurses, shifts, vtype=GRB.BINARY, name="schedule")

model.setObjective(
    gp.quicksum(schedule[n, s] for n in nurses for s in shifts),
    GRB.MINIMIZE
)

for shift in shifts:
    model.addConstr(
        gp.quicksum(schedule[n, shift] for n in nurses) >= min_required[shift],
        name=f"min_staff_{shift}"
    )

for nurse in nurses:
    model.addConstr(
        gp.quicksum(schedule[nurse, s] for s in shifts) <= 3,
        name=f"max_shifts_{nurse}"
    )

for nurse in nurses:
    # Labor rule: 8-hour rest required between shifts
    model.addConstr(
        schedule[nurse, 'Mon_Day'] + schedule[nurse, 'Mon_Night'] <= 1,
        name=f"no_double_{nurse}_Mon"
    )
    model.addConstr(
        schedule[nurse, 'Tue_Day'] + schedule[nurse, 'Tue_Night'] <= 1,
        name=f"no_double_{nurse}_Tue"
    )

model.optimize()

print("Optimal schedule:")
for nurse in nurses:
    assigned = [s for s in shifts if schedule[nurse, s].X > 0.5]
    print(f"{nurse}: {', '.join(assigned)}")

Esto modela el problema de programación utilizando variables binarias. Minimiza los turnos totales respetando las necesidades de personal, las horas máximas y los períodos de descanso obligatorios.

Optimización del portafolio financiero

Relación riesgo-rentabilidad

La optimización del portafolio equilibra los rendimientos esperados con el riesgo. El modelo clásico de Markowitz:

• Maximizar: Rendimiento esperado
• Sujeto a: Riesgo (varianza) por debajo del umbral
• Restricciones: Restricciones presupuestarias, requisitos de diversificación, límites normativos.

Esto es programación cuadrática. El rendimiento es lineal en las ponderaciones del portafolio, pero la varianza es cuadrática (implica productos de ponderaciones).

Consideraciones prácticas

La optimización real del portafolio incluye:

• Costes de transacción (la compra/venta conlleva comisiones)
• Restricciones de números enteros (no se pueden comprar fracciones de algunos activos)
• Requisitos normativos (no puede superar el 10 % en un solo valor).
• Restricciones de reequilibrio (no cambiar el portafolio existente de forma demasiado drástica)

Los gestores de activos realizan estas optimizaciones a diario, gestionando miles de millones en capital. El tiempo de resolución del modelo influye directamente en la ejecución de la estrategia comercial.

Conclusión

Hemos cubierto muchos temas, desde la instalación de Gurobi hasta la creación de modelos complejos de cadena de suministro.

Ahora, en lugar de debatir opiniones en una sala de reuniones, puedes mostrar el código en la pantalla. «Este es el plan matemáticamente óptimo». Eso cambia la conversación. Deja de adivinar y empieza a demostrar.

Anímate y pruébalo con tu próximo problema complicado, ese conflicto de horarios o esa restricción presupuestaria que has estado evitando. Quizás descubras que la respuesta perfecta estaba escondida en tus datos desde el principio.

Y si deseas perfeccionar aún más tus habilidades de optimización, consulta nuestros cursos Introducción a la programación lineal e Introducción a la optimización en Python para seguir aprendiendo.