Programmation linéaire : Résolution de problèmes d'optimisation dans le monde réel

Les responsables des opérations sont confrontés à un défi récurrent : trop de décisions à prendre, trop de contraintes et aucune solution évidente pour trouver la meilleure option. Un réseau de distribution doit minimiser les coûts de carburant sur des dizaines d'itinéraires tout en respectant les délais de livraison, les capacités des véhicules et les horaires des chauffeurs.

Ces deux problèmes partagent une structure mathématique. Lorsque vos objectifs et contraintes peuvent être exprimés sous forme de relations linéaires, vous travaillez sur un problème de programmation linéaire. Nous accordons une grande importance à la programmation linéaire, car elle permet de trouver des solutions optimales lorsque l'on travaille avec des ressources limitées et des exigences concurrentes.

Ce qui rend la programmation linéaire si efficace, c'est sa garantie : s'il existe une solution réalisable, l'algorithme trouvera la solution optimale. Bien entendu, les applications concrètes correspondent rarement parfaitement aux exemples présentés dans les manuels, mais la compréhension du cadre de base vous aide à reconnaître les cas où l'optimisation peut remplacer les conjectures.

Ce guide vous accompagne depuis les bases jusqu'aux implémentations fonctionnelles de Python. Nous progresserons à partir de problèmes simples à deux variables que vous pouvez visualiser géométriquement jusqu'à des scénarios complexes nécessitant des solutions algorithmiques. Vous acquerrez à la fois la théorie mathématique qui sous-tend l'optimisation et les compétences pratiques nécessaires pour mettre en œuvre vous-même des solutions.

Qu'est-ce que la programmation linéaire ?

La programmation linéaire optimise une fonction objectif linéaire soumise à des contraintes linéaires. Dans le cadre d'un projet de routage de distribution sur lequel j'ai travaillé, l'objectif était de minimiser la distance totale parcourue tout en respectant certaines contraintes telles que la capacité des véhicules et les délais de livraison.

Comprendre la structure de base

Chaque problème de programmation linéaire comporte trois éléments : des variables de décision, une fonction objectif et des contraintes.

Les variables de décision représentent les choix que vous effectuez. Dans les problèmes de routage, les variables binaires peuvent indiquer quel véhicule se rend à quel endroit. Dans la planification de la production, les variables peuvent représenter les quantités fabriquées.

La fonction objectif définit ce que vous optimisez. Il doit s'agir d'une combinaison linéaire de vos variables de décision. Les contraintes définissent les règles et les limites de votre problème. Elles se présentent sous trois formes : égalités, inégalités inférieures ou égales, ou inégalités supérieures ou égales.

from scipy.optimize import linprog

c = [10, 15]
A_ub = [[1, 0], [0, 1]]
b_ub = [100, 80]
A_eq = [[1, 1]]
b_eq = [150]
bounds = [(0, None), (0, None)]

result = linprog(c, A_ub=A_ub, b_ub=b_ub, A_eq=A_eq, b_eq=b_eq, 
                 bounds=bounds, method='highs')

print(f"Optimal solution: Truck 1 = {result.x[0]:.1f}, Truck 2 = {result.x[1]:.1f}")
print(f"Total cost: ${result.fun:.2f}")

Le code ci-dessus minimise le coût total pour deux variables de décision, sous réserve de limites individuelles et d'une exigence de couverture totale. Les coefficients objectifs [10, 15] représentent le coût unitaire, les contraintes d'inégalité limitent la plage de chaque variable et la contrainte d'égalité garantit une couverture totale.

Interprétation géométrique

La compréhension de la programmation linéaire a transformé ma perception de l'optimisation d'un point de vue géométrique. Chaque contrainte définit un demi-espace, et leur intersection forme la région réalisable. Cette région est toujours un polytope convexe, ce qui signifie que toute ligne entre deux points intérieursreste à l'intérieur.

Voici l'idée essentielle : les solutions optimales se trouvent toujours aux sommets de la région réalisable. Se déplacer le long d'un bord peut soit améliorer votre objectif, soit ne pas l'améliorer, donc vous continuez à vous déplacer jusqu'à atteindre un coin. Cette propriété rend les algorithmes de programmation linéaire efficaces.

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(0, 8, 400)
y1 = (10 - x) / 2
y2 = 12 - 2*x

plt.figure(figsize=(10, 8))
plt.plot(x, y1, 'r-', label='x + 2y ≤ 10', linewidth=2)
plt.plot(x, y2, 'b-', label='2x + y ≤ 12', linewidth=2)

y_feasible = np.minimum(y1, y2)
y_feasible = np.maximum(y_feasible, 0)
plt.fill_between(x, 0, y_feasible, where=(y_feasible >= 0), 
                 alpha=0.3, color='green', label='Feasible region')

vertices = [(0, 0), (0, 5), (14/3, 8/3), (6, 0)]
for v in vertices:
    plt.plot(v[0], v[1], 'ko', markersize=10)
    obj_value = 3*v[0] + 4*v[1]
    plt.annotate(f'({v[0]:.1f}, {v[1]:.1f})\nObj: {obj_value:.1f}',
                 xy=v, xytext=(v[0]+0.3, v[1]+0.3))

plt.xlim(-0.5, 8)
plt.ylim(-0.5, 8)
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.grid(True, alpha=0.3)
plt.title('Geometric View: Optimal Solution at Vertex (4.7, 2.7)')
plt.show()

Cette visualisation présente la solution optimale au sommet (4,7, 2,7) où deux contraintes se croisent. La région convexe réalisable garantit l'absence de vallées cachées où les algorithmes pourraient se bloquer, assurant ainsi que les optimums locaux correspondent aux optimums globaux.

Transformer les défis du monde réel

Le plus difficile n'est pas de résoudre les problèmes mathématiques, mais de transformer des problèmes complexes en formulations claires. La définition des variables et des contraintes prend souvent plus de temps que l'exécution de l'optimisation elle-même.

Définir les variables décisionnelles implique d'identifier les choix fondamentaux. Pour le routage, vous pouvez utiliser des variables binaires pour l'attribution des emplacements des véhicules ou ajouter des variables continues pour l'ordre des visites afin de simplifier les contraintes.

Construire des contraintes implique de traduire les règles métier en inégalités. Cela met en évidence des hypothèses implicites. Lorsqu'un responsable indique « chaque site a besoin d'une livraison », cela signifie-t-il exactement une livraison ou au moins une livraison ? Ces détails modifient complètement la formulation.

Voici un exemple de formulation utilisant PuLP:

from pulp import *

prob = LpProblem("Food_Bank_Routing", LpMinimize)

trucks = ['Truck_A', 'Truck_B', 'Truck_C']
centers = ['North', 'South', 'East', 'West', 'Central']

x = LpVariable.dicts("route", 
                     [(i, j) for i in trucks for j in centers],
                     cat='Binary')

distances = {
    ('Truck_A', 'North'): 15, ('Truck_A', 'South'): 20,
    ('Truck_A', 'East'): 10, ('Truck_A', 'West'): 25,
    ('Truck_A', 'Central'): 5,
    ('Truck_B', 'North'): 18, ('Truck_B', 'South'): 15,
    ('Truck_B', 'East'): 12, ('Truck_B', 'West'): 22,
    ('Truck_B', 'Central'): 8,
    ('Truck_C', 'North'): 20, ('Truck_C', 'South'): 25,
    ('Truck_C', 'East'): 15, ('Truck_C', 'West'): 18,
    ('Truck_C', 'Central'): 10,
}

prob += lpSum([distances[i, j] * x[i, j] 
               for i in trucks for j in centers])

for j in centers:
    prob += lpSum([x[i, j] for i in trucks]) == 1

max_stops = {'Truck_A': 3, 'Truck_B': 2, 'Truck_C': 3}
for i in trucks:
    prob += lpSum([x[i, j] for j in centers]) <= max_stops[i]

prob.solve()

print(f"Status: {LpStatus[prob.status]}")
print(f"Total distance: {value(prob.objective)} miles")
for i in trucks:
    route = [j for j in centers if value(x[i, j]) == 1]
    print(f"{i} visits: {', '.join(route)}")

La formulation ci-dessus utilise des variables binaires pour l'affectation des camions aux centres, minimise la distance totale, garantit que chaque centre reçoive exactement une livraison et respecte les limites de capacité des camions.

Les modèles de problèmes classiques fournissent des gabarits. Le régime alimentaire permet de minimiser les coûts tout en répondant aux besoins nutritionnels. Les problèmes de transport minimisent les frais d'expédition. Ceci s'appliquait directement à mon propre défi en matière de routage. Reconnaître ces modèles accélère la formulation, car il est rare que l'on soit confronté à des problèmes véritablement nouveaux.

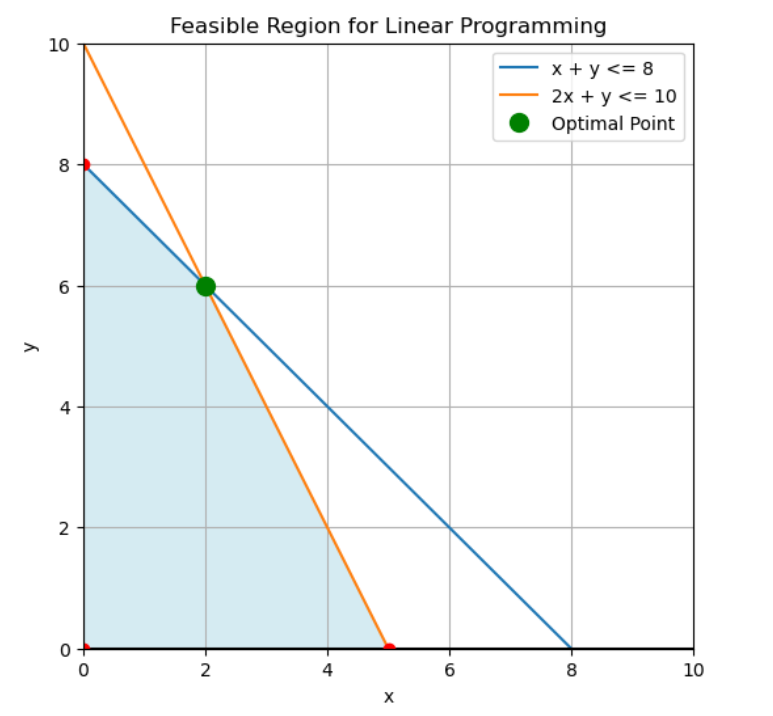
La programmation linéaire identifie les solutions optimales aux sommets des régions réalisables définies par des contraintes. Image par l'auteur

Méthodes de résolution et approches algorithmiques

Comprendre le fonctionnement des algorithmes a modifié ma perception de l'appel à linprog(). Il ne s'agit pas de boîtes noires, mais de procédures mathématiques sophistiquées.

Algorithme simplex

L'algorithme simplex, développé par George Dantzig en 1947, constitue le point de départ. Son principe : parcourir systématiquement chaque sommet vers le sommet adjacent, en améliorant constamment l'objectif, jusqu'à atteindre l'optimum.

L'algorithme maintient un tableau et effectue des opérations de pivot pour se déplacer entre les sommets. Chaque itération améliore l'objectif ou détermine l'optimalité en sélectionnant un élément pivot et en effectuant une mise à jour à l'aide d'opérations sur les lignes.

from scipy.optimize import linprog
import numpy as np

c = [-3, -2]
A_ub = [[2, 1], [2, 3], [3, 1]]
b_ub = [18, 42, 24]
bounds = [(0, None), (0, None)]

result = linprog(c, A_ub=A_ub, b_ub=b_ub, bounds=bounds, method='highs')

print(f"Optimal solution: x1 = {result.x[0]:.2f}, x2 = {result.x[1]:.2f}")
print(f"Maximum value: {-result.fun:.2f}")
print(f"Iterations: {result.nit}")

Le code ci-dessus illustre la résolution d'un problème de maximisation à l'aide de la méthode du simplexe en inversant les coefficients de l'objectif. Le solveur se déplace systématiquement entre les sommets de la région réalisable définie par les contraintes, atteignant la solution optimale en quelques itérations seulement. Dans les problèmes plus complexes, la méthode du simplexe permet de trouver l'optimum en beaucoup moins d'étapes que le nombre de sommets réalisables, souvent en moins de 20 itérations, même avec des milliers de possibilités.

Méthodes des points intérieurs

Alors que la méthode simplex traverse les frontières, les méthodes des points intérieurs naviguent à l'intérieur de la région réalisable. Pour les problèmes d'optimisation de portefeuilles importants comprenant des centaines d'actifs, la méthode simplex peut devenir lente, tandis que les méthodes des points intérieurs permettent d'obtenir des résultats en quelques secondes.

Le principal avantage réside dans la complexité en temps polynomial. L'algorithme de Karmarkar (1984) a rendu les méthodes des points intérieurs pratiques, en équilibrant l'amélioration de l'objectif tout en restant loin des limites de contrainte. Les solveurs modernes tels que Gurobi choisissent automatiquement entre la méthode simplex et la méthode des points intérieurs en fonction des caractéristiques du problème.

Méthode graphique pour deux variables

Pour les problèmes à deux variables, je les résous toujours graphiquement dans un premier temps. Cela développe l'intuition qui se transpose à des dimensions supérieures. Définissez les contraintes graphiques, identifiez la région réalisable et déterminez quel coin optimise l'objectif.

from scipy.optimize import linprog

c = [-30, -40]
A_ub = [[2, 1], [1, 2]]
b_ub = [100, 80]
bounds = [(0, None), (0, None)]

result = linprog(c, A_ub=A_ub, b_ub=b_ub, bounds=bounds, method='highs')

print(f"Bread loaves: {result.x[0]:.0f}")
print(f"Cakes: {result.x[1]:.0f}")
print(f"Maximum profit: ${-result.fun:.0f}")

Ce problème de production boulangère vise à maximiser les bénéfices tirés de la vente de pains et de gâteaux, en tenant compte des contraintes liées aux heures d'ouverture du four et à la décoration. La solution indique quel point d'angle est géométriquement optimal, ce qui rend concret le comportement de saut de sommet de l'algorithme.

Applications dans divers secteurs

La programmation linéaire applique le même cadre mathématique pour résoudre des problèmes dans des domaines très différents.

Fabrication et production

La planification de la production a constitué ma première application sérieuse. Le problème du mix de production détermine les quantités à fabriquer, avec des variables représentant la production, des objectifs maximisant le profit et des contraintes reflétant les limitations en matière de ressources.

from pulp import *

products = ['Phone', 'Tablet', 'Laptop']

profits = {'Phone': 120, 'Tablet': 200, 'Laptop': 350}
assembly_time = {'Phone': 2, 'Tablet': 3, 'Laptop': 5}
testing_time = {'Phone': 1, 'Tablet': 1.5, 'Laptop': 2}

assembly_available = 500
testing_available = 200
min_production = {'Phone': 50, 'Tablet': 30, 'Laptop': 20}

model = LpProblem("Production_Planning", LpMaximize)
production = LpVariable.dicts("produce", products, lowBound=0, cat='Integer')

model += lpSum([profits[p] * production[p] for p in products])
model += lpSum([assembly_time[p] * production[p] for p in products]) <= assembly_available
model += lpSum([testing_time[p] * production[p] for p in products]) <= testing_available

for p in products:
    model += production[p] >= min_production[p]

model.solve()

print(f"Status: {LpStatus[model.status]}")
for p in products:
    print(f"{p}: {production[p].varValue:.0f} units")
print(f"Total profit: ${value(model.objective):,.0f}")

Le modèle ci-dessus optimise la production électronique sur trois gammes de produits, en équilibrant la capacité d'assemblage et de test avec les exigences minimales de production.

Les problèmes de mélange permettent d'optimiser les mélanges répondant aux spécifications à un coût minimal, comme le mélange d'aliments pour répondre aux exigences nutritionnelles tout en minimisant les coûts.

Transport et logistique

Le problème du transport est un autre exemple étudié. La structure classique comprend des sources avec des approvisionnements et des destinations avec des demandes, ce qui minimise le coût total du transport.

warehouses = ['Warehouse_A', 'Warehouse_B', 'Warehouse_C']
supply = {'Warehouse_A': 300, 'Warehouse_B': 400, 'Warehouse_C': 200}

customers = ['Customer_1', 'Customer_2', 'Customer_3', 'Customer_4']
demand = {'Customer_1': 200, 'Customer_2': 150, 'Customer_3': 250, 'Customer_4': 200}

costs = {
    ('Warehouse_A', 'Customer_1'): 8,  ('Warehouse_A', 'Customer_2'): 6,
    ('Warehouse_A', 'Customer_3'): 10, ('Warehouse_A', 'Customer_4'): 7,
    ('Warehouse_B', 'Customer_1'): 9,  ('Warehouse_B', 'Customer_2'): 12,
    ('Warehouse_B', 'Customer_3'): 8,  ('Warehouse_B', 'Customer_4'): 11,
    ('Warehouse_C', 'Customer_1'): 14, ('Warehouse_C', 'Customer_2'): 7,
    ('Warehouse_C', 'Customer_3'): 10, ('Warehouse_C', 'Customer_4'): 12,
}

model = LpProblem("Transportation", LpMinimize)

routes = [(w, c) for w in warehouses for c in customers]
shipments = LpVariable.dicts("ship", routes, lowBound=0)

model += lpSum([costs[i, j] * shipments[i, j] for (i, j) in routes])

for w in warehouses:
    model += lpSum([shipments[w, c] for c in customers]) <= supply[w]

for c in customers:
    model += lpSum([shipments[w, c] for w in warehouses]) >= demand[c]

model.solve()

Les problèmes de flux de réseau généralisent le transport à des graphes comportant des nœuds de transbordement. J'ai lu que les compagnies aériennes utilisent largement cette méthode pour la planification des horaires de l'équipage et l'acheminement des avions.

Services financiers et soins de santé

Dans les applications financières, la budgétisation des investissements sélectionne les projets maximisant le rendement sous réserve des contraintes budgétaires :

projects = {
    'Project_A': {'return': 25000, 'cost': 100000, 'staff': 5},
    'Project_B': {'return': 30000, 'cost': 150000, 'staff': 7},
    'Project_C': {'return': 20000, 'cost': 80000, 'staff': 4},
}

budget = 300000
staff_available = 15

model = LpProblem("Capital_Budgeting", LpMaximize)
select = LpVariable.dicts("select", projects.keys(), cat='Binary')

model += lpSum([projects[p]['return'] * select[p] for p in projects])
model += lpSum([projects[p]['cost'] * select[p] for p in projects]) <= budget
model += lpSum([projects[p]['staff'] * select[p] for p in projects]) <= staff_available

model.solve()

Les systèmes de santé sont confrontés à des défis d'optimisation permanents. J'ai été consulté au sujet d'un problème de planification dans une clinique qui consistait à affecter les infirmières à des quarts de travail tout en respectant les exigences en matière de compétences et l'équilibre

Applications technologiques modernes

La programmation linéaire apparaît également de manière inattendue dans l'apprentissage automatique. La sélection des caractéristiques peut être formulée comme la minimisation de l'erreur de prédiction soumise à des contraintes de parcimonie. Le cloud utilise l'allocation des ressources entre les systèmes distribués.

Complexité et performance informatiques

La complexité est importante lorsque les problèmes passent du stade d'exemples théoriques à celui de systèmes de production.

Complexité de l'algorithme Simplex

Simplex présente un niveau de complexité remarquable. Il présente des performances exponentielles dans le pire des cas, mais excellentes dans le cas moyen. Les cas pathologiques tels que le cube de Klee-Minty nécessitent l'examen de chaque sommet, mais les problèmes typiques n'exigent que l'examen d'une petite fraction, avec une échelle approximativement quadratique.

J'ai évalué cela en résolvant des problèmes générés aléatoirement et de taille croissante :

import time
import numpy as np
from scipy.optimize import linprog

def benchmark_simplex(num_vars, num_constraints):
    c = np.random.randn(num_vars)
    A_ub = np.random.randn(num_constraints, num_vars)
    b_ub = np.random.rand(num_constraints) * 10
    
    start = time.time()
    result = linprog(c, A_ub=A_ub, b_ub=b_ub, method='simplex')
    elapsed = time.time() - start
    
    return elapsed, result.nit

problem_sizes = [(10, 20), (50, 100), (100, 200), (200, 400)]

for n_vars, n_const in problem_sizes:
    times, iterations = [], []
    for _ in range(10):
        t, it = benchmark_simplex(n_vars, n_const)
        times.append(t)
        iterations.append(it)
    print(f"{n_vars}x{n_const}: {np.mean(times):.4f}s, {np.mean(iterations):.1f} iterations")

Mes tests de performance ont démontré que le doublement de la taille du problème augmentait le temps de calcul de moins de 4 fois, confirmant ainsi un comportement quasi polynomial pour les distributions typiques.

Améliorations des performances

Les solveurs modernes offrent des performances remarquables grâce au prétraitement, au traitement parallèle et à la sélection automatique d'algorithmes. Le prétraitement peut réduire automatiquement la taille du problème de 30 % ou plus avant la résolution.

La dégénérescence se produit lorsque plusieurs contraintes sont strictes à l'optimum, ce qui peut entraîner un effet de cycle. J'ai rencontré ce problème lorsque deux itinéraires présentaient des coûts identiques. Les solveurs utilisent des techniques de perturbation pour éviter les cycles, bien que les problèmes dégénérés soient résolus plus lentement.

Une instabilité numérique peut survenir lorsque les problèmes sont mal dimensionnés. Le mélange de montants monétaires (en milliers de dollars) et de quantités (unités individuelles) a généré des avertissements du solveur. Le redimensionnement a immédiatement résolu le problème.

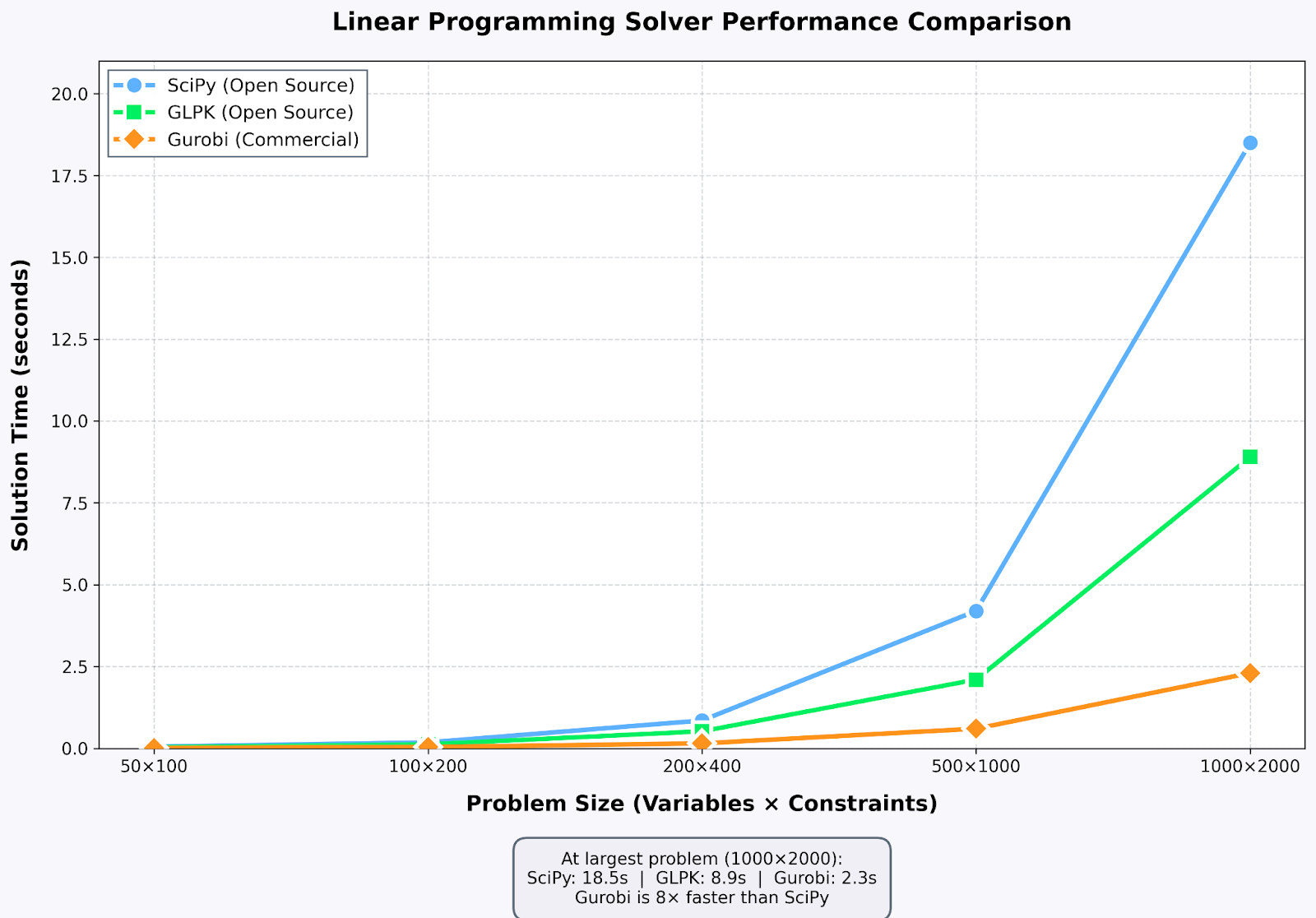
Comparaison des performances des solveurs : les solutions commerciales sont particulièrement performantes pour les problèmes à grande échelle. Image par l'auteur

Outils logiciels et mise en œuvre

Le choix des outils a un impact considérable sur la productivité. Je suis passé du codage manuel simplex à l'utilisation de solveurs professionnels capables de traiter des problèmes beaucoup plus complexes.

Solveurs commerciaux et langages de modélisation

CPLEX et Gurobi dominent le domaine de l'optimisation industrielle, offrant des performances nettement supérieures à celles des alternatives open source pour les problèmes de grande envergure. J'ai utilisé la licence académique de Gurobi pour des travaux sur la chaîne logistique. Les difficultés rencontrées lors de la prise de notes avec SciPy sont résolues en quelques instants.

PuLP est mon outil Python de prédilection. Il fournit une API claire pour la formulation de modèles résolus par divers backends :

from pulp import *

model = LpProblem("my_problem", LpMaximize)

x = LpVariable("x", lowBound=0)
y = LpVariable("y", lowBound=0)

model += 3*x + 2*y
model += x + y <= 100
model += 2*x + y <= 150

model.solve()

print(f"Used solver: {model.solver}")
print(f"Status: {LpStatus[model.status]}")

La couche d'abstraction désigne un code indépendant du solveur qui s'exécute sur différents systèmes. Pyomo propose des fonctionnalités plus avancées pour l'optimisation complexe, notamment la programmation non linéaire et stochastique.

Alternatives cloud et open source

Les plateformes cloud offrent des services d'optimisation pour les problèmes irréguliers à grande échelle. Vous téléchargez les données relatives au problème et recevez les solutions via l'API. L'architecture sans serveur est élégante, mais plus lente que les solveurs locaux pour les problèmes de petite envergure.

GLPK (GNU Linear Programming Kit) est un outil open source fiable et performant. Je l'utilise pour l'enseignement et pour des projets personnels. HiGHS est un nouveau solveur qui affiche des performances remarquables. SciPy a récemment adopté HiGHS comme backend par défaut, et mes tests de performance ont démontré qu'il était comparable à Gurobi sur de nombreux problèmes.

Exemples de programmation linéaire

Travailler à partir d'exemples complets permet de mieux comprendre que la théorie seule.

Exemple 1 : Problème alimentaire

Le problème classique de l'alimentation consiste à minimiser les coûts tout en répondant aux besoins nutritionnels :

from pulp import *

foods = {
    'Oatmeal': {'cost': 0.50, 'calories': 110, 'protein': 4, 'vitamin': 2},
    'Chicken': {'cost': 2.50, 'calories': 250, 'protein': 30, 'vitamin': 0},
    'Eggs':    {'cost': 0.80, 'calories': 155, 'protein': 13, 'vitamin': 1},
    'Milk':    {'cost': 1.20, 'calories': 150, 'protein': 8, 'vitamin': 4},
    'Bread':   {'cost': 0.30, 'calories': 80, 'protein': 3, 'vitamin': 0}
}

min_calories, min_protein, min_vitamin = 2000, 50, 10

model = LpProblem("Diet_Optimization", LpMinimize)
servings = LpVariable.dicts("servings", foods.keys(), lowBound=0)

model += lpSum([foods[f]['cost'] * servings[f] for f in foods])
model += lpSum([foods[f]['calories'] * servings[f] for f in foods]) >= min_calories
model += lpSum([foods[f]['protein'] * servings[f] for f in foods]) >= min_protein
model += lpSum([foods[f]['vitamin'] * servings[f] for f in foods]) >= min_vitamin

model.solve()

print(f"Total cost: ${value(model.objective):.2f}")
for food in foods:
    if servings[food].varValue > 0.01:
        print(f"{food}: {servings[food].varValue:.2f} servings")

La formule ci-dessus permet de déterminer la combinaison la plus économique d'aliments répondant aux besoins nutritionnels quotidiens. Cela démontre que les solutions LP optimales ne sont pas toujours applicables sans contraintes supplémentaires liées à la variété, aux goûts ou aux préférences alimentaires.

Ce même cadre peut également servir de base à des décisions commerciales telles que l'optimisation des calendriers de production ou l'allocation des budgets marketing.

Exemple 2 : Planification pluriannuelle

La planification multi-périodes examine comment les niveaux de stock influencent les besoins futurs sur plusieurs périodes :

days = ['Monday', 'Tuesday', 'Wednesday', 'Thursday', 'Friday']

centers = {
    'North': {'daily_demand': [100, 80, 90, 110, 85], 'capacity': 250},
    'South': {'daily_demand': [120, 100, 95, 105, 130], 'capacity': 300},
}

delivery_cost = {'Monday': 50, 'Tuesday': 50, 'Wednesday': 50,
                 'Thursday': 50, 'Friday': 70}

model = LpProblem("Multiperiod_Routing", LpMinimize)

deliveries = LpVariable.dicts("deliver",
                              [(c, d) for c in centers for d in days],
                              lowBound=0)
inventory = LpVariable.dicts("inventory",
                            [(c, d) for c in centers for d in days],
                            lowBound=0)

model += lpSum([delivery_cost[d] * deliveries[c, d] 
                for c in centers for d in days])

for c in centers:
    for i, day in enumerate(days):
        if i == 0:
            model += inventory[c, day] == deliveries[c, day] - centers[c]['daily_demand'][i]
        else:
            prev_day = days[i-1]
            model += (inventory[c, day] == inventory[c, prev_day] + 
                     deliveries[c, day] - centers[c]['daily_demand'][i])
        model += inventory[c, day] <= centers[c]['capacity']

model.solve()

Les modèles multi-périodes augmentent la taille du problème, mais permettent une optimisation sophistiquée. Le modèle regroupe les livraisons les jours où les coûts sont moins élevés, en utilisant la capacité de stockage pour réduire les coûts globaux.

Programmation mixte en nombres entiers

De nombreux problèmes impliquent des décisions distinctes : construire ou ne pas construire une installation, affecter ou ne pas affecter un employé. Cela nécessite une programmation mixte en nombres entiers (MIP), qui étend la programmation linéaire avec des variables entières et binaires.

Introduction et méthode de branche et limite

Les problèmes de routage nécessitent des décisions entières. La variable binaire x[i][j] indique si le véhicule i se rend à l'emplacement j. Les véhicules ne peuvent pas effectuer de visites fractionnées.

La méthode de recherche par branches et limites explore systématiquement un espace de solutions discrètes en résolvant des relaxations LP continues :

from pulp import *

model_continuous = LpProblem("Continuous", LpMaximize)
x_cont = LpVariable("x", lowBound=0)
y_cont = LpVariable("y", lowBound=0)

model_continuous += 3*x_cont + 4*y_cont
model_continuous += x_cont + 2*y_cont <= 10
model_continuous += 2*x_cont + y_cont <= 12

model_continuous.solve()
print(f"Continuous: x={x_cont.varValue:.2f}, y={y_cont.varValue:.2f}")

model_integer = LpProblem("Integer", LpMaximize)
x_int = LpVariable("x", lowBound=0, cat='Integer')
y_int = LpVariable("y", lowBound=0, cat='Integer')

model_integer += 3*x_int + 4*y_int
model_integer += x_int + 2*y_int <= 10
model_integer += 2*x_int + y_int <= 12

model_integer.solve()
print(f"Integer: x={x_int.varValue:.0f}, y={y_int.varValue:.0f}")

La solution entière diffère de l'arrondi de la solution continue. La méthode Branch-and-bound permet de trouver la solution entière optimale, mais à un coût de calcul nettement plus élevé.

Quand utiliser la programmation entière ?

Utilisez des variables entières lorsque les décisions sont intrinsèquement discrètes : ouverture d'installations, affectation de travailleurs, acheminement de véhicules. Les optimisations sur le marché obligataire nécessitent souvent des solutions mixtes entières. Les variables continues peuvent produire des affectations fractionnaires non pertinentes, tandis que les variables binaires fournissent des solutions applicables.

Cependant, la programmation entière est considérablement plus coûteuse. Les problèmes comportant des centaines de variables entières peuvent prendre des heures, contre quelques secondes pour les LP continus. Si les quantités produites sont importantes, l'intégralité importe moins, car l'arrondi n'affecte pratiquement pas les solutions. Veuillez toujours résoudre d'abord la relaxation continue afin de vérifier les limites avant de vous engager dans une programmation entière complète.

Conclusion

La programmation linéaire transforme votre approche des problèmes d'optimisation. Le même cadre mathématique s'applique à des domaines très différents, du routage à la planification de la production en passant par la gestion de portefeuille.

Commencez par des problèmes simples à deux variables que vous pouvez visualiser géométriquement. Mettre en œuvre le simplexe de base pour appréhender le fonctionnement interne des solveurs commerciaux. Travaillez avec des formulations réelles, en traduisant les exigences commerciales en contraintes mathématiques.

Pour approfondir vos connaissances, nous vous invitons à explorer nos cours Introduction à l'optimisation en Python et Algèbre linéaire pour la science des données afin de renforcer vos bases mathématiques. Notre cursus professionnel de scientifique en apprentissage automatique avec Python constitue une autre excellente option.