Gurobi: Otimização matemática para problemas complexos

Os solucionadores básicos e os métodos de tentativa e erro têm dificuldade quando as variáveis aumentam. O Gurobi lida com essas complexidades com rapidez e precisão, resolvendo em segundos problemas que, de outra forma, poderiam levar horas. Essa é a diferença entre torcer por um plano que dá certo e provar matematicamente que você tem o plano ideal.

Este tutorial te mostracomo usar o poderoso solucionador comercial chamado Gurobi . Vou te mostrar como instalar a biblioteca Python, criar seu primeiro modelo e avançar para problemas mais complexos, como programação mista inteira.

Entendendo a otimização matemática e o papel da Gurobi

Antes de escrever código, é bom entender o que otimização realmente significa. Esse contexto mostra quando usar o Gurobi em vez das abordagens de programação padrão.

O que é otimização matemática?

A otimização matemática encontra a melhor solução entre todas as possíveis. Você define o que significa “melhor” (minimizar custos, maximizar lucros, minimizar tempo), o que você controla (variáveis de decisão) e quais são os limites que você enfrenta (restrições). O otimizador procura entre as soluções possíveis para encontrar a melhor.

Isso é diferente da programação tradicional, onde você define etapas exatas. Com a otimização, você descreve o problema matematicamente e deixa que o solucionador descubra como resolvê-lo. Você não está escrevendo uma lógica do tipo “se isso, então aquilo”, mas sim definindo relações e deixando que os algoritmos encontrem os melhores valores.

A importância da Gurobi na otimização

Por que a Gurobi se destaca

O Gurobi é sempre considerado um dos otimizadores comerciais mais rápidos que existem. Os benchmarks geralmente mostram que ele supera significativamente as alternativas de código aberto em problemas de grande escala. Essa velocidade é importante quando você está fazendo otimização de hora em hora ou precisa de resultados dentro de prazos bem curtos.

Adoção pela indústria

Empresas dos setores de logística, finanças, energia e saúde usam o Gurobi para sistemas de produção. A FedEx otimiza as rotas de entrega, enquanto as empresas financeiras alocam bilhões em portfólios. As empresas de energia planejam a geração de energia. Não se trata de exercícios acadêmicos, mas de sistemas que lidam com dinheiro real e restrições reais.

Recursos do Solver

O Gurobi lida com programação linear (LP), programação mista inteira (MIP), programação quadrática (QP) e muito mais. Inclui algoritmos de última geração, como otimização simultânea, em que vários métodos de solução são executados em paralelo e o mais rápido vence. Você ganha confiabilidade e rapidez sem precisar escolher os algoritmos manualmente.

Configurando o Gurobi

A instalação do Gurobi é bem simples. Depois de configurado, ele funciona perfeitamente como Python .

Instalação e configuração

Baixe e instale

Acesseo site da Gurobi e baixe o instalador para o seu sistema operacional. Inclui o otimizador, a interface gurobipy e a documentação . Execute o instaladorcom as configurações padrão, a menos que você precise de um caminho personalizado.

Depois de instalar, dá uma olhada se funcionou:

import gurobipy as gp
print(f"Gurobi version: {gp.__version__}")

Aqui, a gente verifica a instalação imprimindo o número da versão. Uma impressão bem-sucedida mostra que seu ambiente está pronto.

Opções de licenciamento

O Gurobi precisa de uma licença pra qualquer coisa além de pequenos problemas de teste. Suas opções:

• Licença de avaliação gratuita: Avaliação de 30 dias. Pede no site da Gurobi usando o teu e-mail do trabalho.
• Licença acadêmica: De graça para professores e alunos. Confirme seu e-mail acadêmico para ter acesso ilimitado, o que é perfeito para aprender.
• Licença comercial: Necessário para os negócios. Os preços variam de acordo com a escala. As licenças para usuários nomeados são ideais para cientistas de dados individuais, enquanto as licenças flutuantes permitem que as equipes compartilhem a capacidade.
• Licença na nuvem: Pague conforme o uso. Sem custos iniciais, só paga pelo que usar. Ótimo pra tarefas ocasionais de otimização.

Eu uso a licença acadêmica para aprender e a comercial para produção. O teste te dá bastante tempo para explorar antes de se comprometer.

Configuração do ambiente

Configuração do Python

O Gurobi funciona com Python 3.7+. Recomendo usar um ambiente virtual pra evitar conflitos:

python -m venv gurobi_env
gurobi_env\Scripts\activate
source gurobi_env/bin/activate
pip install gurobipy

Esses comandos criam um espaço de trabalho limpo e puxam a biblioteca.

Integração com o Jupyter Notebook

Para desenvolvimento interativo, os notebooks funcionam muito bem com o Gurobi:

pip install jupyter
jupyter notebook
import gurobipy as gp
print("Gurobi ready!")

Esse trecho instala o Jupyter, inicia o servidor e faz uma verificação rápida pra garantir que o Gurobi carregue corretamente no notebook.

Quando NÃO usar o Gurobi

O Gurobi é poderoso, mas nem sempre é a escolha certa.

• Problemas simples: Se você tem 50 variáveis e restrições lineares básicas, solucionadores gratuitos como scipy.optimize.linprog ou Excel Solverfuncionam bem.

• Custo: As licenças comerciais são caras. Para ferramentas internas não críticas, opções de código aberto como CBC ou GLPK (via PuLP) podem ser suficientes.

• Heurística: Se você precisa de uma resposta “boa o suficiente” em milissegundos para um jogo em tempo real, heurísticas (como algoritmos genéticos) geralmente superam solucionadores exatos.

Use o Gurobi quando os problemas forem grandes (mais de 10 mil variáveis) ou você precisar de recursos avançados, como restrições quadráticas.

Compatibilidade da plataforma

O Gurobi funciona no Windows, macOS e Linux. Ambientes em nuvem como AWS, Azure e Google Cloud oferecem suporte ao Gurobi por meio de seus mercados. Implementei modelos Gurobi nas três principais nuvens sem problemas específicos da plataforma.

Modelos de otimização de edifícios

Com o Gurobi instalado, vamos criar seu primeiro modelo. Esses conceitos básicos se aplicam a todos os problemas que você vai resolver.

Principais componentes de um modelo de otimização

Cada modelo tem três partes essenciais:

Variáveis de decisão

Essas são as escolhas que o otimizador faz. No planejamento da produção, isso pode ser “unidades do Produto A” e “unidades do Produto B”. Você define as variáveis; o Gurobi atribui os valores.

Função objetiva

Esse é o seu objetivo, o que você quer aumentar ou diminuir. Maximizar o lucro (3*product_a + 5*product_b) ou minimizar o custo. Você tem um objetivo por modelo.

Restrições

Esses são os seus limites. Você não pode produzir mais do que a capacidade da fábrica nem gastar mais do que o seu orçamento. As restrições definem quais soluções são realmente possíveis.

Melhores práticas de formulação

Use nomes de variáveis claros. Em vez de x[1], use produce_product_a. Isso poupa horas de depuração mais tarde, como explicarei na seção de solução de problemas.

Mantenha as restrições simples. Dividir uma lógica complexa em restrições menores e mais simples torna seu modelo mais fácil de ler e depurar.

Modern Gurobi: A API Matrix

Se você tem experiência em ciência de dados, a modelagem baseada em loops pode parecer lenta. O Gurobi 13.0+ oferece uma API Matrix que usa matrizes NumPy, tornando a construção de modelos 10 a 50 vezes mais rápida.

Aqui tá como fica um modelo de padaria usando vetores:

import gurobipy as gp
import numpy as np

# Data
prices = np.array([2.0, 5.0])
resources = np.array([[0.5, 2.0], [1.0, 1.0]])
limits = np.array([100.0, 80.0])

model = gp.Model("bakery_matrix")
x = model.addMVar(shape=2, name="x")

model.setObjective(prices @ x, gp.GRB.MAXIMIZE)
model.addConstr(resources @ x <= limits, name="constraints")

model.optimize()

Essa sintaxe A @ x <= b é mais clara e padrão para sistemas de produção.

Criando um modelo simples de programação linear

Vamos resolver um problema prático: uma padaria decidindo quantos pães e bolos assar para maximizar o lucro.

Configuração do problema:

- Lucro do pão: $2 | Farinha: 0,5 kg

- Lucro do bolo: $5 | Farinha: 2 kg

- Farinha disponível: 100 kg

- Capacidade do forno: 80 itens

Aqui está o modelo:

import gurobipy as gp
from gurobipy import GRB

model = gp.Model("bakery_optimization")

bread = model.addVar(name="bread", vtype=GRB.CONTINUOUS, lb=0)
cake = model.addVar(name="cake", vtype=GRB.CONTINUOUS, lb=0)

model.setObjective(2 * bread + 5 * cake, GRB.MAXIMIZE)

model.addConstr(0.5 * bread + 2 * cake <= 100, name="flour_limit")
model.addConstr(bread + cake <= 80, name="oven_capacity")

model.optimize()

if model.status == GRB.OPTIMAL:
    print(f"Optimal profit: ${model.objVal:.2f}")
    print(f"Bake {bread.X:.2f} loaves of bread")
    print(f"Bake {cake.X:.2f} cakes")
else:
    print("No optimal solution found")

Esse código inicializa o modelo, define variáveis e estabelece a meta de lucro. Ele aplica as restrições que definimos acima e resolve o plano ideal.

Entendendo os registros do solucionador

Quando você executa model.optimize(), o Gurobi gera um log. Veja como ler:

Gurobi Optimizer version 13.0.0...
Presolve removed 0 rows and 0 columns
...
Explored 0 nodes (2 simplex iterations) in 0.01 seconds
Optimal objective  2.800000000e+02

• Presolve: O Gurobi simplifica o seu problema antes de resolvê-lo. “Linhas removidas” quer dizer que ele achou restrições que não precisavam estar lá.
• Iteraçõessimples: Quantos passos o algoritmo deu. Números altos em pequenos problemas podem indicar problemas de formulação.
• Objetivoideal: Seu resultado final (por exemplo, lucro de $280).
• Lacuna: Para problemas inteiros, isso mostra a diferença entre a melhor solução encontrada até agora e a melhor solução teórica.

Ver o registro ajuda a perceber se um modelo está “travado” ou só trabalhando bastante.

Os conceitos aqui são diretamente proporcionais. Quer você tenha 10 variáveis ou 10.000, o padrão continua o mesmo.

Tipos de problemas avançados suportados pelo Gurobi

A programação linear é só o começo. O Gurobi lida com tipos complexos que capturam as nuances do mundo real, incluindo os novos recursos MINLP não convexos na versão 13.0.

Programação linear mista inteira

O que o torna diferente

A programação mista inteira (MIP) permite que as variáveis sejam inteiras. Não dá pra construir fábricas de 0,7, então você precisa de soluções inteiras.

Aplicações no mundo real

Localização das instalações: Abrir um warehouse na cidade A? Sim (1) ou Não (0).

Programação da produção: Os tamanhos dos lotes geralmente precisam ser números inteiros.

Projeto de rede: As decisões de roteamento geralmente são binárias. O tráfego passa por um link ou não passa.

Exemplo: localização das instalações

import gurobipy as gp
from gurobipy import GRB

model = gp.Model("facility_location")

cities = ['CityA', 'CityB', 'CityC']
fixed_costs = {'CityA': 10000, 'CityB': 8000, 'CityC': 12000}

open_warehouse = model.addVars(cities, vtype=GRB.BINARY, name="open")

model.setObjective(
    gp.quicksum(fixed_costs[city] * open_warehouse[city] for city in cities),
    GRB.MINIMIZE
)

model.addConstr(gp.quicksum(open_warehouse[city] for city in cities) >= 2)

model.optimize()

print("Open warehouses in:")
for city in cities:
    if open_warehouse[city].X > 0.5:
        print(f"  {city}")

Aqui, usamos variáveis binárias para decidir se vamos abrir um warehouse. O modelo minimiza os custos fixos e garante que pelo menos duas instalações continuem funcionando.

Programação quadrática e não linear

Programação quadrática (QP)

Quando seu objetivo inclui termos quadrados ou produtos variáveis, você tem um QP. A otimização do portfólio é um exemplo clássico porque o risco (variância) é quadrático.

Programação com restrições quadráticas (QCP)

As restrições também podem ser quadráticas. Pense em problemas que envolvam círculos ou limites curvos.

Exemplo: otimização de portfólio

import gurobipy as gp
from gurobipy import GRB
import numpy as np

model = gp.Model("portfolio")

assets = ['StockA', 'StockB', 'StockC']
expected_returns = [0.12, 0.18, 0.10]

covariance = np.array([
    [0.04, 0.01, 0.02],
    [0.01, 0.09, 0.03],
    [0.02, 0.03, 0.05]
])

weights = model.addVars(len(assets), name="weight", lb=0, ub=1)

model.setObjective(
    gp.quicksum(expected_returns[i] * weights[i] for i in range(len(assets))),
    GRB.MAXIMIZE
)

model.addConstr(gp.quicksum(weights[i] for i in range(len(assets))) == 1)

risk_expr = gp.quicksum(
    covariance[i][j] * weights[i] * weights[j]
    for i in range(len(assets))
    for j in range(len(assets))
)
model.addConstr(risk_expr <= 0.05, name="risk_limit")

model.optimize()

print("Optimal portfolio allocation:")
for i, asset in enumerate(assets):
    print(f"{asset}: {weights[i].X * 100:.1f}%")

Essa configuração lida com a otimização do portfólio. Ele maximiza os retornos enquanto limita rigorosamente o risco total (variância) usando restrições quadráticas.

Tipos de problemas adicionais suportados

Programação de cone de segunda ordem (SOCP)

Problemas que envolvem restrições geométricas, como definir um cone ou um limite circular, se encaixam nessa categoria. É comum em otimização robusta e projeto de engenharia.

Programação quadrática mista inteira (MIQP)

Combina variáveis inteiras com objetivos ou restrições quadráticas. Útil na otimização discreta com relações não lineares.

O Gurobi suporta todos esses tipos nativamente. Você não precisa reformular os problemas para se adequarem a um solucionador específico, o Gurobi detecta automaticamente o tipo de problema e aplica os algoritmos apropriados.

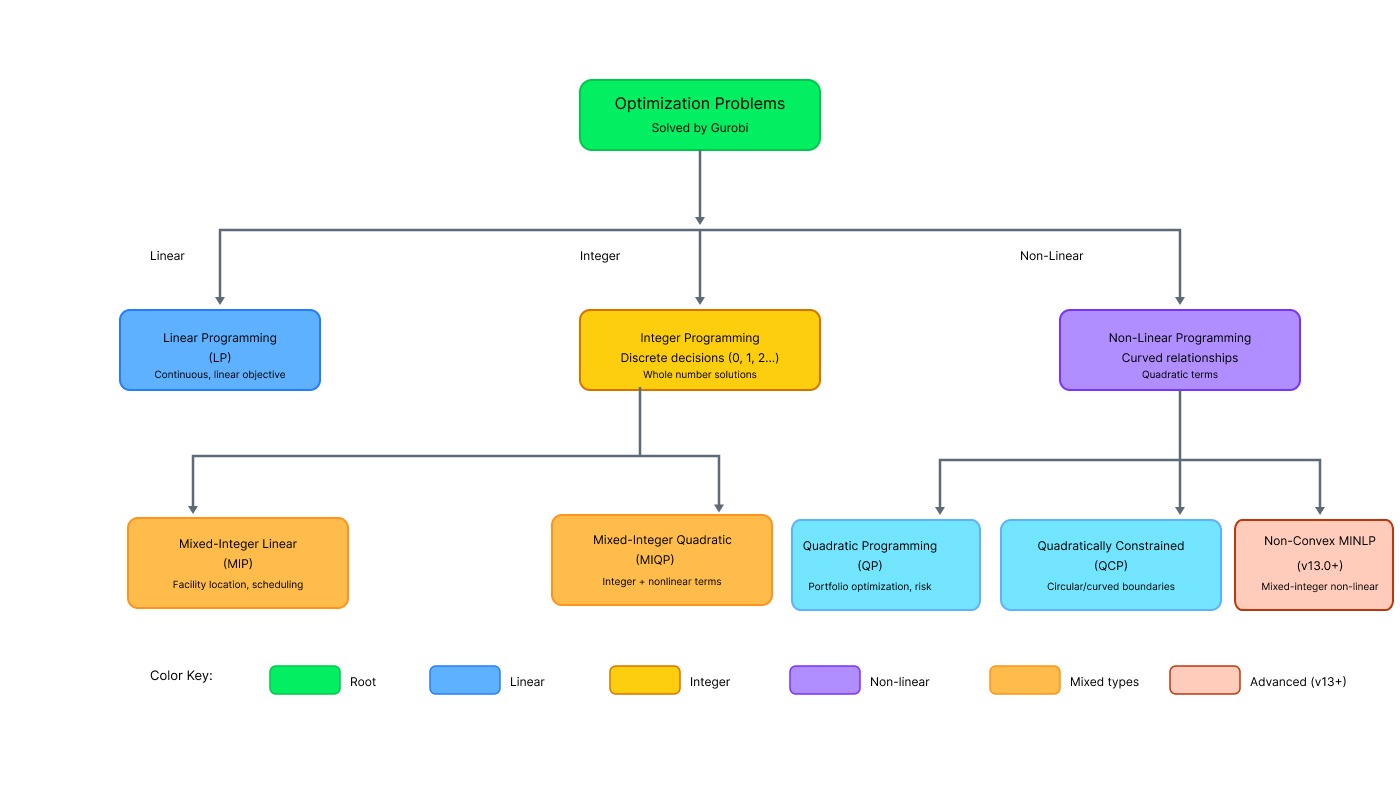
Tipos de problemas de otimização suportados pelo Gurobi. Imagem do autor.

Algoritmos Gurobi e suas aplicações

Seleção do algoritmo

O Gurobi escolhe os algoritmos automaticamente, mas conhecer as opções ajuda na hora de resolver problemas de lentidão nas soluções.

Valores do método:

• -1 (padrão): Deixe o Gurobi decidir

• 0: Simplex primitivo (ótimo para a maioria dos LPs)

• 1: Simplex duplo (ótimo quando se começa com algo inviável)

• 2: Barreira (ideal para modelos grandes ou QP)

• 3: Concorrente (executa vários métodos, escolhe o mais rápido)

• 4: Concorrente determinístico

• 5: Simplex Concorrente Determinístico

• PDHG (Método de Primeira Ordem: O Gurobi 13.0 também inclui o PDHG, um método baseado em gradiente ideal para LPs massivos que se encaixam em GPUs.

Dá uma olhada no log do solucionador pra ver qual foi executado (por exemplo, “Modelo de barreira resolvido...”

Quando substituir: Se o padrão demorar horas, tente Barreira para modelos enormes ou Concorrente para problemas imprevisíveis.

model.Params.Method = 2
model.Params.BarConvTol = 1e-8

Isso escolhe explicitamente o método Barreira e torna a tolerância mais rígida, o que ajuda quando se lida com conjuntos de dados enormes ou sensíveis.

Usando os recursos avançados do Gurobi

Depois de dominar o básico, o Gurobi oferece ferramentas poderosas para resolver problemas em escala empresarial.

Otimização distribuída

Para modelos enormes que demoram muito tempo em uma única máquina, você pode dividir o trabalho. A otimização distribuída da Gurobi usa vários computadores para resolver um único problema mais rápido.

Você escolhe uma máquina como “gerente” e as outras como “trabalhadoras”. O gerente manda partes da árvore de pesquisa para os funcionários, que resolvem em paralelo. Isso é exagero para modelos pequenos, mas essencial para problemas de cadeia de suprimentos global ou programação de companhias aéreas.

Otimização multiobjetiva

A vida real raramente tem só um objetivo. Você pode querer aumentar o lucro e diminuir o impacto ambiental.

O Gurobi resolve isso permitindo que você defina prioridades. Você pode dizer para “maximizar o lucro primeiro e, em seguida, minimizar o desperdício sem reduzir o lucro em mais de 10%”. Ou então, você pode ponderá-los: Objective = 0.7 * Profit - 0.3 * Waste.

# Multi-objective example
model.setObjectiveN(profit_expr, index=0, priority=2, name="Profit")
model.setObjectiveN(waste_expr, index=1, priority=1, name="Waste")

Interação em tempo real e retornos de chamada

Às vezes, você quer dar uma força enquanto o Gurobi tá resolvendo. Os callbacks permitem que você execute código personalizado em momentos específicos, tipo sempre que uma nova solução for encontrada.

Eu uso callbacks pra parar mais cedo se uma solução for “boa o suficiente” ou pra colocar heurísticas personalizadas que eu sei que funcionam pros meus dados específicos.

Recursos da nuvem

Fazer otimização no seu laptop é legal para desenvolvimento, mas a produção geralmente precisa de mais potência. O Gurobi Cloud permite que você transfira o trabalho pesado para a AWS, Azure ou a própria Instant Nuvem da Gurobi. Você paga só pelo tempo de resolução, o que é perfeito pra cargas de trabalho pesadas e esporádicas.

Melhores práticas de modelagem prática

Escrever modelos eficientes precisa de estratégia. Aqui estão algumas dicas para manter seu código limpo e rápido.

Estratégias de formulação de modelos

Comece de forma simples e vá aumentando a complexidade aos poucos.

Não crie um modelo com 50 restrições logo no primeiro dia. Comece com a lógica central, verifique-a e, em seguida, refine-a. Passei muito tempo depurando modelos complexos só para descobrir que o erro estava no básico.

Use nomes significativos para variáveis e restrições

x1 = model.addVar(name="x1")
model.addConstr(x1 + x2 <= 100, name="c1")

units_produced = model.addVar(name="units_produced")
model.addConstr(
    units_produced + units_stored <= warehouse_capacity,
    name="warehouse_capacity_limit"
)

Repara na diferença: o segundo bloco mostra bem a lógica do negócio. Como eu disse antes, isso evita dores de cabeça com depuração.

Pré-processar dados

Valide seus dados antes de modelar. Verifique se há valores ausentes ou restrições impossíveis. É chato encontrar erros nos dados depois de passar três horas resolvendo problemas.

Dá uma olhada nos seus dados de forma adequada

O Gurobi lida bem com a precisão numérica, mas valores extremos causam problemas. Se os custos forem na casa dos milhões e as quantidades na casa dos milésimos, ajuste-os para magnitudes parecidas:

# Instead of cost = 10000000 and quantity = 0.0001
# Scale to cost = 10 (in millions) and quantity = 100 (in 1/1000 units)

Problemas numéricos são raros em modelos bem dimensionados, mas comuns em modelos mal dimensionados.

Considerações sobre estabilidade numérica

O Gurobi usa aritmética de ponto flutuante, que não é infinita. Se sua restrição diz “ x <= 1000000000 ” e sua tolerância é “1e-6 ”, você pode obter resultados estranhos.

Evite restrições do tipo “Big M”, como if y=0 then x <= 1,000,000,000. Em vez disso, escolha o menor limite superior válido (por exemplo, tamanho total do mercado). Limites mais restritos significam soluções mais rápidas e estáveis.

Partidas a quente e modificações do modelo

Raramente você resolve um problema só uma vez. Normalmente, novos dados chegam (por exemplo, demanda atualizada).

Em vez de reconstruir o modelo do zero, use uma inicialização a quente. Você coloca a solução anterior no Gurobi como ponto de partida. Como o plano ideal de ontem deve ser parecido com o de hoje, o Gurobi pode pular boa parte do trabalho de pesquisa.

# Warm start example
bread.Start = 40  # Start search assuming we bake 40 loaves

Interfaces de programação e integração

API Python da Gurobi

Usamos gurobipy porque é Pythonic. Suporta sobrecarga de operadores (x + y <= 5) e se integra diretamente com pandas e NumPy. É a maneira mais popular de usar o Gurobi para ciência de dados.

Integração com outras linguagens

Os sistemas de produção geralmente funcionam em C++, Java ou .NET por causa da velocidade. O Gurobi dá suporte a todos eles. Os conceitos (Variáveis, Restrições, Objetivos) são os mesmos; só muda a sintaxe.

Para fluxos de trabalho entre linguagens, costumo criar protótipos em Python (codificação rápida) e implantar em C++ (execução rápida), usando os formatos de arquivo da Gurobi (.mps ou .lp) para mover modelos entre eles.

Suporte à linguagem de modelagem

O Gurobi também se conecta a linguagens de modelagem específicas, como AMPL e GAMS, ou até mesmo o Excel.

- AMPL/GAMS: Ótimo pra quem pesquisa só matemática e não quer escrever código de software.

- Excel: Ótimo pra fazer protótipos rápidos ou mostrar pros parceiros de negócios um modelo que eles podem mexer sem precisar instalar o Python.

Otimização e ajuste de desempenho

Ajustando o fluxo de trabalho

Não sintonize aleatoriamente. Siga este processo:

1. Medida de referência: Execute com as configurações padrão e anote o tempo de resolução.

2. Defina limites rígidos primeiro: Os sistemas de produção precisam de TimeLimit.

3. Troque precisão por velocidade: Só relaxe MIPGap se o negócio permitir.

4. Teste de dimensionamento de threads: Mais threads ≠ mais rápido (retorno decrescente após 4-8).

# Example: Production deployment
model.Params.TimeLimit = 300  # Hard 5-min cutoff for API response
baseline_time = model.Runtime

if baseline_time > 240:  # If cutting it close
    model.Params.MIPGap = 0.02  # Accept 2% suboptimality
    # Business rationale: 2% cost increase < late delivery penalty

Referências de desempenho

Os benchmarks mostram que o Gurobi sempre supera os solucionadores de código aberto por ordens de magnitude em problemas MIP difíceis. Embora o scipy lide bem com LPs pequenos, o Gurobi se destaca quando a complexidade aumenta. Você pode encontrar benchmarks comparativos no site de Hans Mittelmann, que acompanha o desempenho do solucionador de forma independente.

Depuração e resolução de problemas

Impossibilidade do modelo

Quando o Gurobi diz que “o modelo não é viável”, é porque suas restrições estão em conflito. Nenhuma solução satisfaz todos eles ao mesmo tempo.

Descubra as restrições conflitantes:

model.computeIIS()
model.write("infeasible.ilp")

print("Conflicting constraints:")
for c in model.getConstrs():
    if c.IISConstr:
        print(f"  {c.ConstrName}: {c.ConstrExpr}")

Isso calcula o Subsistema Inconsistente Irredutível (IIS) e mostra exatamente quais restrições estão em conflito entre si.

Modelos ilimitados

Um modelo ilimitado significa que o objetivo pode melhorar infinitamente. Normalmente indica restrições ausentes.

Verificar:

- Você vinculou todas as variáveis? addVar(lb=0, ub=1000)

- As restrições estão bem definidas?

- A função objetivo está certa?

Usando registros do solucionador

Ative o registro detalhado para ver o que o Gurobi está fazendo:

model.Params.OutputFlag = 1
model.Params.LogToConsole = 1
model.Params.LogFile = "gurobi.log"

Isso ativa a saída detalhada e salva uma cópia em um arquivo local, dando a você um histórico detalhado do processo de resolução.

Tratamento de dados

Nos aplicativos reais, os dados vêm de arquivos, não de listas codificadas.

import pandas as pd

# Load data
df = pd.read_csv("facility_costs.csv")
fixed_costs = dict(zip(df['city'], df['fixed_cost']))

# Validate BEFORE modeling
if any(c < 0 for c in fixed_costs.values()):
    raise ValueError("Costs cannot be negative")

Esse padrão, Carregar-Validar-Modelar, evita erros silenciosos.

Aplicações reais do Gurobi

A teoria é ótima, mas vamos ver como as indústrias realmente usam isso.

Otimização da cadeia de suprimentos

Projeto da rede de distribuição

A FedEx, uma UPS e uma Amazon usam os conceitos do curso Análise da Cadeia de Suprimentos em Python para minimizar custos e, ao mesmo tempo, cumprir as garantias de entrega.

Vamos usar a API Matrix para este exemplo para lidar com a escala de forma eficiente.

import gurobipy as gp
from gurobipy import GRB
import numpy as np

# 1. Data Generation
factories = ["F1", "F2"]
warehouses = ["W1", "W2", "W3"]
customers = ["C1", "C2", "C3", "C4"]

# Cost matrices (Factory->Warehouse, Warehouse->Customer)
transport_fw = np.array([[2.0, 4.0, 5.0], [3.0, 1.0, 6.0]])
transport_wc = np.array([
    [1.5, 2.0, 3.0, 4.0],
    [3.0, 1.0, 2.0, 2.5],
    [5.0, 4.0, 1.0, 1.5]
])

# Capacity and Demand
factory_cap = np.array([1000, 1000])
demand = np.array([300, 500, 400, 600])

try:
    with gp.Model("SupplyChain_Matrix") as model:
        # 2. Variables (Matrix Form)
        # Flow F->W and W->C
        flow_fw = model.addMVar((len(factories), len(warehouses)), name="fw")
        flow_wc = model.addMVar((len(warehouses), len(customers)), name="wc")
        
        # Binary decision: Open warehouse?
        open_w = model.addMVar(len(warehouses), vtype=GRB.BINARY, name="open")

        # 3. Objective: Minimize Transport + Fixed Costs
        fixed_cost = 5000
        obj = (transport_fw * flow_fw).sum() + \
              (transport_wc * flow_wc).sum() + \
              (fixed_cost * open_w).sum()
        model.setObjective(obj, GRB.MINIMIZE)

        # 4. Constraints
        # Factory capacity (sum rows of flow_fw <= cap)
        model.addConstr(flow_fw.sum(axis=1) <= factory_cap, name="Cap")

        # Customer demand (sum cols of flow_wc >= demand)
        model.addConstr(flow_wc.sum(axis=0) >= demand, name="Demand")

        # Flow balance: Inflow to W == Outflow from W
        model.addConstr(flow_fw.sum(axis=0) == flow_wc.sum(axis=1), name="Balance")

        # Warehouse capacity linking: Flow out <= BigM * OpenBinary
        model.addConstr(flow_wc.sum(axis=1) <= 2000 * open_w, name="Link")

        model.optimize()

        if model.Status == GRB.OPTIMAL:
            print(f"Optimal Cost: ${model.ObjVal:,.2f}")
            print(f"Open Warehouses: {open_w.X}")

except gp.GurobiError as e:
    print(f"Error: {e}")

Essa abordagem vetorizada (addMVar, sum(axis=1)) lida com milhares de variáveis na hora, evitando loops lentos do Python.

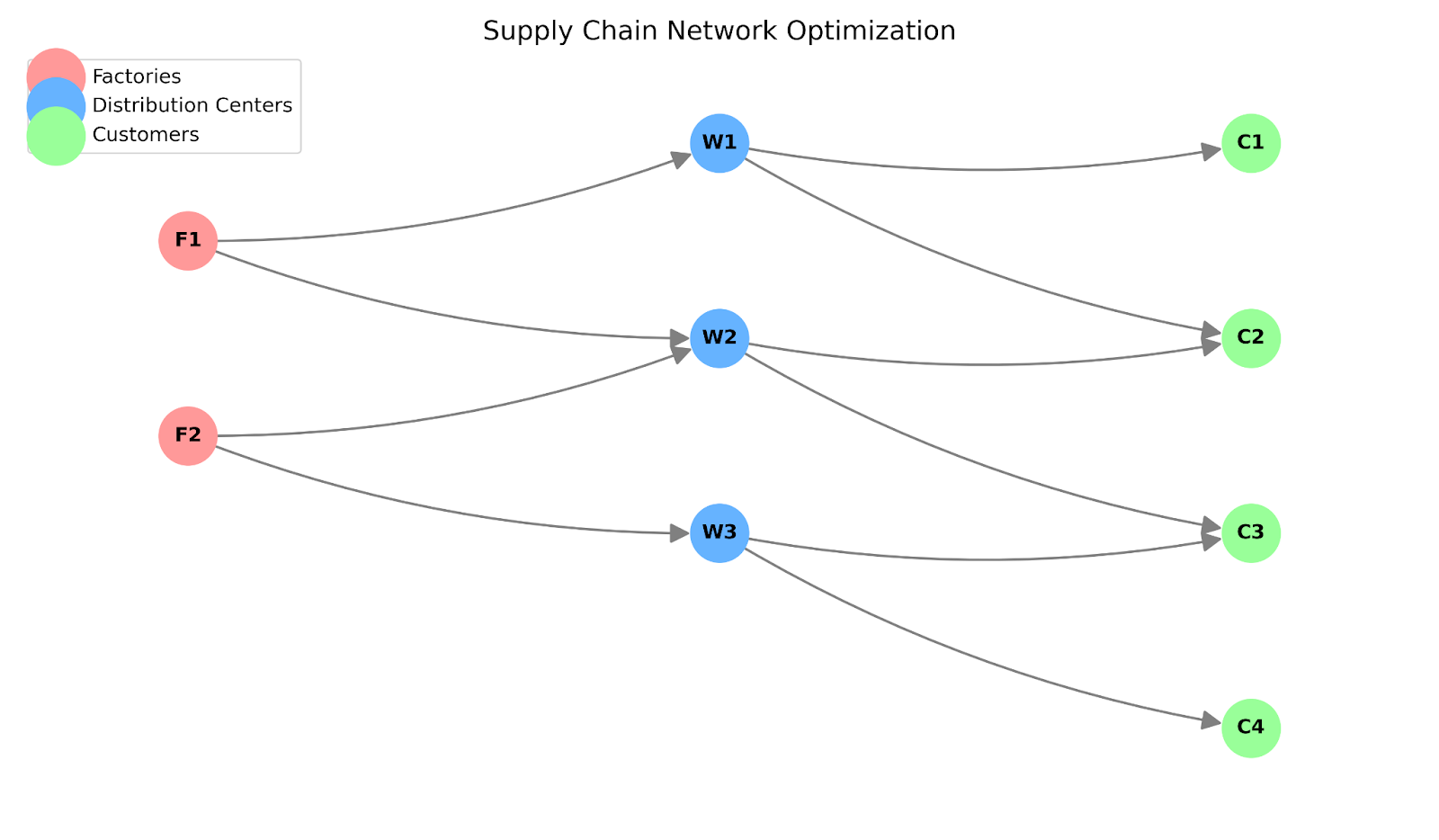
Gráfico da rede da cadeia de suprimentos. Imagem do autor.

Otimização do estoque

É complicado equilibrar os custos de pedidos, estoque e falta de produtos. Com uma demanda incerta, isso vira uma otimização estocástica, que a Gurobi resolve usando modelagem de cenários.

Planejamento da força de trabalho

Planejamento de turnos

Os hospitais e call centers precisam organizar os horários dos funcionários, respeitando as necessidades de pessoal, as regras trabalhistas e as preferências.

Isso é pura programação mista inteira. Cada tarefa é uma escolha binária. Um hospital com 100 enfermeiros e 50 turnos tem 5.000 variáveis para administrar.

Exemplo: programação de enfermeiras

import gurobipy as gp
from gurobipy import GRB

model = gp.Model("nurse_scheduling")

nurses = ['Alice', 'Bob', 'Carol', 'Dave']
shifts = ['Mon_Day', 'Mon_Night', 'Tue_Day', 'Tue_Night']
min_required = {'Mon_Day': 2, 'Mon_Night': 1, 'Tue_Day': 2, 'Tue_Night': 1}

schedule = model.addVars(nurses, shifts, vtype=GRB.BINARY, name="schedule")

model.setObjective(
    gp.quicksum(schedule[n, s] for n in nurses for s in shifts),
    GRB.MINIMIZE
)

for shift in shifts:
    model.addConstr(
        gp.quicksum(schedule[n, shift] for n in nurses) >= min_required[shift],
        name=f"min_staff_{shift}"
    )

for nurse in nurses:
    model.addConstr(
        gp.quicksum(schedule[nurse, s] for s in shifts) <= 3,
        name=f"max_shifts_{nurse}"
    )

for nurse in nurses:
    # Labor rule: 8-hour rest required between shifts
    model.addConstr(
        schedule[nurse, 'Mon_Day'] + schedule[nurse, 'Mon_Night'] <= 1,
        name=f"no_double_{nurse}_Mon"
    )
    model.addConstr(
        schedule[nurse, 'Tue_Day'] + schedule[nurse, 'Tue_Night'] <= 1,
        name=f"no_double_{nurse}_Tue"
    )

model.optimize()

print("Optimal schedule:")
for nurse in nurses:
    assigned = [s for s in shifts if schedule[nurse, s].X > 0.5]
    print(f"{nurse}: {', '.join(assigned)}")

Isso modela o problema de programação usando variáveis binárias. Isso minimiza o total de turnos, respeitando as necessidades de pessoal, o número máximo de horas e os períodos de descanso obrigatórios.

Otimização do portfólio financeiro

Relação risco-retorno

A otimização do portfólio equilibra os retornos esperados com o risco. O modelo clássico de Markowitz:

• Maximize: Retorno esperado
• Sujeito a: Risco (variação) abaixo do limite
• Restrições: Restrições orçamentárias, requisitos de diversificação, limites regulatórios

Isso é programação quadrática. O retorno é linear nas ponderações do portfólio, mas a variância é quadrática (envolve produtos de ponderações).

Considerações práticas

A otimização real do portfólio inclui:

• Custos de transação (compra/venda tem taxas)
• Restrições inteiras (não dá pra comprar partes fracionárias de alguns ativos)
• Requisitos regulamentares (não pode passar de 10% em um único título)
• Restrições de reequilíbrio (não mude muito o portfólio atual)

Os gestores de ativos fazem essas otimizações todo dia, cuidando de bilhões em capital. O tempo de resolução do modelo afeta diretamente a execução da estratégia de negociação.

Conclusão

A gente falou de um monte de coisas, desde instalar o Gurobi até criar modelos complexos de cadeia de suprimentos.

Agora, em vez de discutir opiniões numa sala de reuniões, você pode colocar o código na tela. “Aqui está o plano matematicamente ideal.” Isso muda a conversa. Você para de adivinhar e começa a provar.

Vá em frente e tente isso no seu próximo problema complicado, aquele conflito de agenda ou aperto no orçamento que você tem evitado. Você pode descobrir que a resposta perfeita estava escondida nos seus dados o tempo todo.

E se você quiser aprimorar ainda mais suas habilidades de otimização, confira nossos cursos Introdução à Programação Linear e Introdução à Otimização em Python para continuar aprendendo.