Tutoriel sur la classification naïve de Bayes à l'aide de Scikit-learn

Qu'est-ce que le classificateur naïf de Bayes ?

Naive Bayes est une technique de classification statistique basée sur le théorème de Bayes. Il s'agit de l'un des algorithmes d'apprentissage supervisé les plus simples. Le classificateur naïf de Bayes est un algorithme rapide, précis et fiable. Les classificateurs naïfs de Bayes offrent une grande précision et une vitesse élevée sur les ensembles de données volumineux.

Le classificateur naïf de Bayes suppose que l'effet d'une caractéristique particulière dans une classe est indépendant des autres caractéristiques. Par exemple, un demandeur de prêt est jugé acceptable ou non en fonction de ses revenus, de ses antécédents en matière de prêts et de transactions, de son âge et de son lieu de résidence. Même si ces caractéristiques sont interdépendantes, elles sont néanmoins considérées de manière indépendante. Cette hypothèse simplifie les calculs, et c'est pourquoi elle est considérée comme naïve. Cette hypothèse est appelée indépendance conditionnelle de classe.

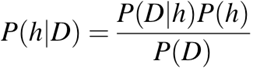
• P(h): la probabilité que l'hypothèse h soit vraie (indépendamment des données). Ceci est connu sous le nom de probabilité a priori d'h.

• P(D): la probabilité des données (indépendamment de l'hypothèse). Ceci est appelé la probabilité a priori.

• P(h|D): la probabilité de l'hypothèse h étant donné les données D. Ceci est appelé probabilité a posteriori.

• P(D|h): la probabilité de l'd e des données étant donné que l'hypothèse h était vraie. Ceci est appelé probabilité a posteriori.

Le processus de classification naïf de Bayes

Lorsque vous effectuez une classification, la première étape consiste à comprendre le problème et à identifier les caractéristiques et les étiquettes potentielles. Les caractéristiques sont les attributs ou les propriétés qui influencent les résultats de l'étiquette. Par exemple, dans le cas d'un prêt, les responsables bancaires identifient la profession, les revenus, l'âge, le lieu de résidence, les antécédents en matière de crédit, l'historique des transactions et la cote de crédit du client. Ces caractéristiques sont considérées comme des éléments qui aident le modèle à classer les clients.

La classification comporte deux phases : une phase d'apprentissage et une phase d'évaluation. Au cours de la phase d'apprentissage, le classificateur entraîne son modèle sur un ensemble de données donné, et au cours de la phase d'évaluation, il teste les performances du classificateur. La performance est évaluée sur la base de divers paramètres tels que l'exactitude, l'erreur, la précision et le rappel.

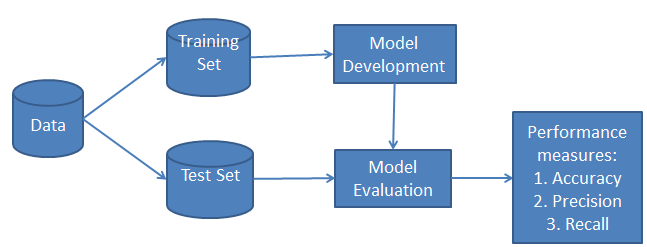
Comment fonctionne le classificateur naïf de Bayes ?

Comprenons le fonctionnement de Naive Bayes à l'aide d'un exemple. Prenons l'exemple des conditions météorologiques et de la pratique sportive. Il est nécessaire de calculer la probabilité de pratiquer un sport. À présent, il est nécessaire de déterminer si les joueurs participeront ou non, en fonction des conditions météorologiques.

Première approche (dans le cas d'une caractéristique unique)

Le classificateur naïf de Bayes calcule la probabilité d'un événement en suivant les étapes suivantes :

• Étape 1: Calculez la probabilité a priori pour les étiquettes de classe données.
• Étape 2: Déterminez la probabilité de vraisemblance avec chaque attribut pour chaque classe.
• Étape 3: Veuillez insérer ces valeurs dans la formule de Bayes et calculer la probabilité a posteriori.
• Étape 4: Déterminez quelle classe présente la probabilité la plus élevée, étant donné que l'entrée appartient à la classe de probabilité la plus élevée.

Afin de simplifier le calcul des probabilités a priori et a posteriori, vous pouvez utiliser les deux tableaux suivants : les tableaux de fréquence et de vraisemblance. Ces deux tableaux vous aideront à calculer la probabilité a priori et a posteriori. Le tableau de fréquence contient la fréquence d'apparition des étiquettes pour toutes les caractéristiques. Il existe deux tableaux de probabilité. Le tableau de vraisemblance 1 présente les probabilités a priori des étiquettes et le tableau de vraisemblance 2 présente la probabilité a posteriori.

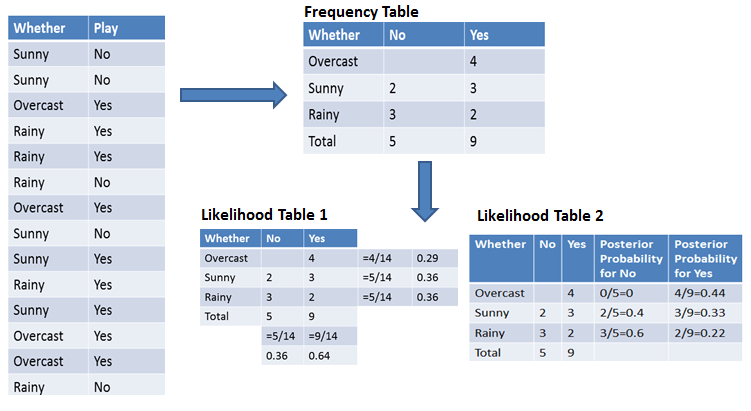
Supposons maintenant que vous souhaitiez calculer la probabilité de jouer lorsque le temps est couvert.

Probabilité de jouer :

P(Oui | Temps couvert) = P(Temps couvert | Oui) × P(Oui) / P(Temps couvert)

Étape 1 : Calculer les probabilités a priori

• P(temps couvert) = 4/14 = 0,29
• P(Oui) = 9/14 = 0,64

Étape 2 : Calculer la probabilité a posteriori

• P(Temps couvert | Oui) = 4/9 = 0,44

Étape 3 : Appliquer la formule de Bayes 

Ici, nous intégrons les probabilités a priori et a posteriori dans la première équation.

P(Oui | Temps couvert) = 0,44 × 0,64 / 0,29 = 0,98

De la même manière, vous pouvez calculer la probabilité de ne pas jouer :

Probabilité de ne pas jouer :

P(Non | Nuageux) = P(Nuageux | Non) × P(Non) / P(Nuageux)

Étape 1 : Calculer les probabilités a priori

• P(temps couvert) = 4/14 = 0,29
• P(Non) = 5/14 = 0,36

Étape 2 : Calculer la probabilité

• P(Temps couvert | Non) = 0/5 = 0

Étape 3 : Appliquer la formule de Bayes

Ici, nous intégrons les probabilités a priori et a posteriori dans l'équation afin d'obtenir la probabilité a posteriori.

P(Non | Temps couvert) = 0 × 0,36 / 0,29 = 0

La probabilité d'une classe « Oui » est plus élevée. Vous pouvez donc déterminer ici si le temps est couvert, auquel cas les joueurs pratiqueront ce sport.

Deuxième approche (dans le cas de caractéristiques multiples)

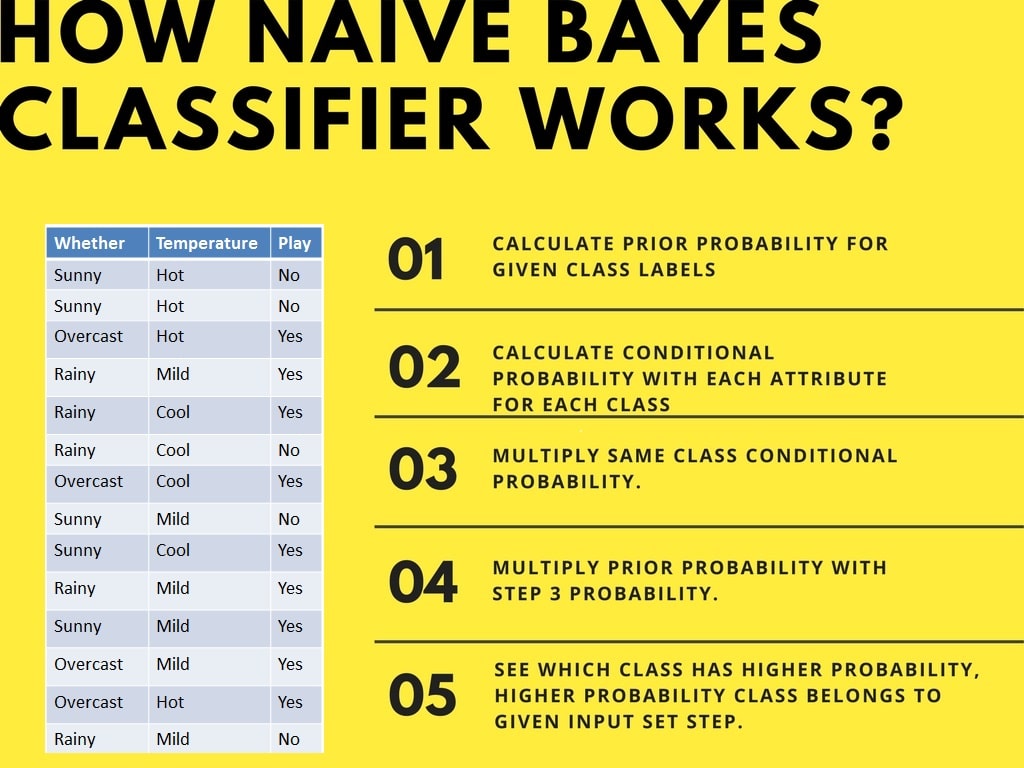
Supposons maintenant que vous souhaitiez calculer la probabilité de jouer lorsque le temps est couvert et que la température est douce.

Probabilité de jouer :

P(Jeu = Oui | Temps = Couvert, Température = Douce) = P(Temps = Couvert, Température = Douce | Jeu = Oui) × P(Jeu = Oui)

En utilisant l'hypothèse d'indépendance naïve de Bayes :

P(Temps = Nuageux, Température = Douce | Activité = Oui) = P(Nuageux | Oui) × P(Douce | Oui)

Étape 1 : Calculer la probabilité a priori

• P(Oui) = 9/14 = 0,64

Étape 2 : Calculer les probabilités

• P(Temps couvert | Oui) = 4/9 = 0,44
• P(Léger | Oui) = 4/9 = 0,44

Étape 3 : Calculer la probabilité combinée

P(Temps = Couvert, Température = Douce | Jouer = Oui) = 0,44 × 0,44 = 0,1936

Étape 4 : Appliquer la formule de Bayes

P(Jeu = Oui | Météo = Nuageux, Température = Douce) = 0,1936 × 0,64 = 0,124

De la même manière, vous pouvez calculer la probabilité de ne pas jouer :

Probabilité de ne pas jouer :

P(Jeu = Non | Temps = Nuageux, Température = Douce) = P(Temps = Nuageux, Température = Douce | Jeu = Non) × P(Jeu = Non)

En utilisant l'hypothèse d'indépendance naïve de Bayes :

P(Temps = Couvert, Température = Douce | Activité = Non) = P(Couverture nuageuse | Non) × P(Température douce | Non)

Étape 1 : Calculer la probabilité a priori

• P(Non) = 5/14 = 0,36

Étape 2 : Calculer les probabilités

• P(Temps couvert | Non) = 0/5 = 0
• P(Léger | Non) = 2/5 = 0,4

Étape 3 : Calculer la probabilité combinée

P(Temps = Couvert, Température = Douce | Activité = Non) = 0 × 0,4 = 0

Étape 4 : Appliquer la formule de Bayes

P(Jeu = Non | Temps = Couvert, Température = Douce) = 0 × 0,36 = 0

La probabilité de la classe « Oui » est plus élevée (0,124 contre 0), donc si le temps est couvert et que la température est douce, les joueurs pratiqueront ce sport.

Construction de classificateurs dans Scikit-learn

Classificateur naïf de Bayes avec un ensemble de données synthétiques

Dans le premier exemple, nous allons générer des données synthétiques à l'aide de scikit-learn, puis entraîner et évaluer l'algorithme gaussien Naive Bayes. 

Génération de l'ensemble de données

Scikit-learn nous fournit un écosystème d'apprentissage automatique qui nous permet de générer des ensembles de données et d'évaluer divers algorithmes d'apprentissage automatique. 

Dans notre cas, nous créons un ensemble de données comprenant six caractéristiques, trois classes et 800 échantillons à l'aide de la fonction ` make_classification() `. 

from sklearn.datasets import make_classification

X, y = make_classification(
    n_features=6,
    n_classes=3,
    n_samples=800,
    n_informative=2,
    random_state=1,
    n_clusters_per_class=1,
)

Nous utiliserons la fonction scatter() de matplotlib.pyplotpour visualiser l'ensemble de données. 

import matplotlib.pyplot as plt

plt.scatter(X[:, 0], X[:, 1], c=y, marker="*");

Comme nous pouvons le constater, il existe trois types d'étiquettes cibles, et nous allons entraîner un modèle de classification multiclasses. 

Test de séparation des trains

Avant de commencer le processus d'entraînement, il est nécessaire de diviser l'ensemble de données en deux parties distinctes : l'entraînement et le test, afin de permettre l'évaluation du modèle. 

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.33, random_state=125
)

Modélisation et formation 

Construisez un modèle générique gaussien naïf bayésien et entraînez-le sur un ensemble de données d'apprentissage. Ensuite, veuillez introduire un échantillon de test aléatoire dans le modèle afin d'obtenir une valeur prédite.

from sklearn.naive_bayes import GaussianNB

# Build a Gaussian Classifier
model = GaussianNB()

# Model training
model.fit(X_train, y_train)

# Predict Output
predicted = model.predict([X_test[6]])

print("Actual Value:", y_test[6])
print("Predicted Value:", predicted[0])

Les valeurs réelles et prévues sont identiques. 

Actual Value: 0
Predicted Value: 0

Évaluation du modèle

Nous n'utiliserons pas le modèle sur un ensemble de données de test non vu. Tout d'abord, nous allons prédire les valeurs pour l'ensemble de données de test et les utiliser pour calculer la précision et le score F1. 

from sklearn.metrics import (
    accuracy_score,
    confusion_matrix,
    ConfusionMatrixDisplay,
    f1_score,
)

y_pred = model.predict(X_test)
accuray = accuracy_score(y_pred, y_test)
f1 = f1_score(y_pred, y_test, average="weighted")

print("Accuracy:", accuray)
print("F1 Score:", f1)

Notre modèle a obtenu des résultats satisfaisants avec les hyperparamètres par défaut. 

Accuracy: 0.8484848484848485
F1 Score: 0.8491119695890328

Pour visualiser la matrice de confusion, nous utiliserons confusion_matrix afin de calculer les vrais positifs et les vrais négatifs, et ConfusionMatrixDisplaypour afficher la matrice de confusion avec les étiquettes.

labels = [0,1,2]
cm = confusion_matrix(y_test, y_pred, labels=labels)
disp = ConfusionMatrixDisplay(confusion_matrix=cm, display_labels=labels)
disp.plot();

Notre modèle a obtenu de très bons résultats, et nous pouvons améliorer ses performances grâce à la mise à l'échelle, au prétraitement des validations croisées et à l'optimisation des hyperparamètres. 

Classificateur naïf de Bayes avec un ensemble de données de prêts

Entraînons le classificateur naïf de Bayes sur l'ensemble de données réel. Nous répéterons la plupart des tâches, à l'exception du prétraitement et de l'exploration des données. 

Chargement des données

Dans cet exemple, nous allons charger les données relatives aux prêts à partir de DataLab à l'aide de la fonction read_csvde pandas. 

import pandas as pd


df = pd.read_csv('loan_data.csv')
df.head()

Exploration des données

Pour mieux comprendre l'ensemble de données, nous utiliserons .info().

• L'ensemble de données comprend 14 colonnes et 9 578 lignes.

• À l'exception de l'purpose, les colonnes sont soit des flottants, soit des entiers. 

• Notre colonne cible est not.fully.paid. 

df.info()

RangeIndex: 9578 entries, 0 to 9577
Data columns (total 14 columns):
#   Column             Non-Null Count  Dtype 
---  ------             --------------  ----- 
0   credit.policy      9578 non-null   int64 
1   purpose            9578 non-null   object
2   int.rate           9578 non-null   float64
3   installment        9578 non-null   float64
4   log.annual.inc     9578 non-null   float64
5   dti                9578 non-null   float64
6   fico               9578 non-null   int64 
7   days.with.cr.line  9578 non-null   float64
8   revol.bal          9578 non-null   int64 
9   revol.util         9578 non-null   float64
10  inq.last.6mths     9578 non-null   int64 
11  delinq.2yrs        9578 non-null   int64 
12  pub.rec            9578 non-null   int64 
13  not.fully.paid     9578 non-null   int64 
dtypes: float64(6), int64(7), object(1)
memory usage: 1.0+ MB

Dans cet exemple, nous allons développer un modèle permettant de prédire les clients qui n'ont pas entièrement remboursé leur prêt. Veuillez examiner la colonne « purpose » et « target » à l'aide du graphique countplot de seaborn. 

import seaborn as sns
import matplotlib.pyplot as plt

sns.countplot(data=df,x='purpose',hue='not.fully.paid')
plt.xticks(rotation=45, ha='right');

Notre ensemble de données présente un déséquilibre qui affectera les performances du modèle. Nous vous invitons à consulter le tutoriel Resample an Imbalanced Dataset (Rééchantillonner un ensemble de données déséquilibré) afin d'acquérir une expérience pratique dans le traitement des ensembles de données déséquilibrés.

Traitement des données 

Nous allons maintenant convertir la colonne « purpose » de type catégoriel en entier à l'aide de la fonction pandas « get_dummies() ».

pre_df = pd.get_dummies(df,columns=['purpose'],drop_first=True)
pre_df.head()

Ensuite, nous définirons les variables caractéristiques (X) et cibles (y), puis nous diviserons l'ensemble de données en ensembles d'apprentissage et de test. 

from sklearn.model_selection import train_test_split

X = pre_df.drop('not.fully.paid', axis=1)
y = pre_df['not.fully.paid']

X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.33, random_state=125
)

Modélisation et formation

La construction et la formation du modèle sont relativement simples. Nous allons entraîner un modèle sur un ensemble de données d'entraînement en utilisant les hyperparamètres par défaut. 

from sklearn.naive_bayes import GaussianNB

model = GaussianNB()

model.fit(X_train, y_train);

Évaluation du modèle

Nous utiliserons la précision et le score f1 pour évaluer les performances du modèle, et il semble que l'algorithme gaussien Naive Bayes ait obtenu de très bons résultats. 

from sklearn.metrics import (
    accuracy_score,
    confusion_matrix,
    ConfusionMatrixDisplay,
    f1_score,
    classification_report,
)

y_pred = model.predict(X_test)

accuray = accuracy_score(y_pred, y_test)
f1 = f1_score(y_pred, y_test, average="weighted")

print("Accuracy:", accuray)
print("F1 Score:", f1)

Accuracy: 0.8206263840556786
F1 Score: 0.8686606980013266

En raison de la nature déséquilibrée des données, nous pouvons constater que la matrice de confusion présente une situation différente. Concernant une cible minoritaire : not fully paid, nous avons davantage d'étiquettes erronées. 

labels = ["Fully Paid", "Not fully Paid"]
cm = confusion_matrix(y_test, y_pred)
disp = ConfusionMatrixDisplay(confusion_matrix=cm, display_labels=labels)
disp.plot();

Si vous rencontrez des difficultés lors de la formation ou de l'évaluation du modèle, vous pouvez consulter le tutoriel sur la classification naïve de Bayes à l'aide du classeur Scikit-learn DataLab. Il est fourni avec un ensemble de données, le code source et les résultats. 

Problème de probabilité nulle

Supposons qu'il n'y ait aucun tuple pour un prêt à risque dans l'ensemble de données ; dans ce scénario, la probabilité a posteriori sera nulle et le modèle ne sera pas en mesure de faire une prédiction. Ce problème est appelé « probabilité nulle » car la fréquence d'apparition de cette classe particulière est nulle.

La solution à ce problème est la correction laplacienne ou transformation de Laplace. La correction par Laplacien est l'une des techniques de lissage. Ici, on peut supposer que l'ensemble de données est suffisamment volumineux pour que l'ajout d'une ligne pour chaque classe n'ait pas d'incidence sur la probabilité estimée. Cela permettra de résoudre le problème des valeurs de probabilité égales à zéro.

Par exemple : Supposons que pour la classe « prêt risqué », il y ait 1 000 tuples d'entraînement dans la base de données. Dans cette base de données, la colonne « revenu » contient 0 tuple pour les faibles revenus, 990 tuples pour les revenus moyens et 10 tuples pour les revenus élevés. Les probabilités de ces événements, sans la correction de Laplace, sont de 0, 0,990 (sur 990/1000) et 0,010 (sur 10/1000).

Veuillez maintenant appliquer la correction laplacienne à l'ensemble de données fourni. Ajoutons un tuple supplémentaire pour chaque paire revenu-valeur. Les probabilités de ces événements :

Avantages de la méthode naïve de Bayes

• Il s'agit non seulement d'une approche simple, mais également d'une méthode rapide et précise pour établir des prévisions.
• Naive Bayes présente un coût de calcul très faible.
• Il est capable de traiter efficacement de grands ensembles de données.
• Il fonctionne bien dans le cas d'une variable de réponse discrète par rapport à une variable continue.
• Il peut être utilisé pour résoudre divers problèmes de prédiction de classes.
• Il est également performant dans le cadre de problèmes d'analyse de texte.
• Lorsque l'hypothèse d'indépendance est valable, un classificateur naïf bayésien est plus performant que d'autres modèles tels que la régression logistique.

Inconvénients de la méthode naïve de Bayes

• L'hypothèse des caractéristiques indépendantes. Dans la pratique, il est pratiquement impossible qu'un modèle obtienne un ensemble de prédicteurs qui soient entièrement indépendants.
• Si aucun tuple d'apprentissage n'existe pour une classe donnée, cela entraîne une probabilité a posteriori nulle. Dans ce cas, le modèle n'est pas en mesure de faire des prévisions. Ce problème est connu sous le nom de problème de probabilité/fréquence nulle.

Conclusion

Félicitations, vous avez terminé ce tutoriel.

Dans ce tutoriel, vous avez découvert l'algorithme Naive Bayes, son fonctionnement, ses hypothèses, ses enjeux, sa mise en œuvre, ses avantages et ses inconvénients. Au cours de votre parcours, vous avez également acquis des compétences en matière de construction et d'évaluation de modèles dans scikit-learn pour les classes binaires et multinomiales.

Naive Bayes est l'algorithme le plus simple et le plus puissant. Malgré les progrès significatifs réalisés dans le domaine de l'apprentissage automatique au cours des deux dernières années, celui-ci a démontré son utilité. Il a été déployé avec succès dans de nombreuses applications, de l'analyse de texte aux moteurs de recommandation.

Si vous souhaitez en savoir plus sur scikit-learn en Python, nous vous invitons à suivre notre cours « Apprentissage supervisé avec scikit-learn » et à consulter notre tutoriel Scikit-Learn « » : Analyse du baseball, partie 1.