Curso
Introdução ao Python
4 h
6.7M
Torne-se um cientista de ML
Domine as habilidades em Python para se tornar um cientista de aprendizado de máquina
O que é o classificador Naive Bayes?
Naive Bayes é uma técnica de classificação estatística baseada no Teorema de Bayes. É um dos algoritmos de aprendizagem supervisionada mais simples. O classificador Naive Bayes é um algoritmo rápido, preciso e confiável. Os classificadores Naive Bayes têm alta precisão e velocidade em grandes conjuntos de dados.
O classificador Naive Bayes assume que o efeito de uma característica específica em uma classe é independente de outras características. Por exemplo, um candidato a empréstimo é aceitável ou não dependendo de sua renda, histórico de empréstimos e transações anteriores, idade e localização. Mesmo que essas características sejam interdependentes, elas ainda são consideradas de forma independente. Essa suposição simplifica o cálculo, e é por isso que é considerada ingênua. Essa suposição é chamada de independência condicional de classe.
-
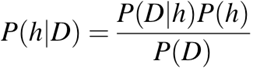
P(h): a chance de a hipótesehser verdadeira (não importa os dados). Isso é conhecido como probabilidade a priori deh. -
P(D): a probabilidade dos dados (sem importar a hipótese). Isso é conhecido como probabilidade a priori. -
P(h|D): a probabilidade da hipóteseh, considerando os dadosD. Isso é conhecido como probabilidade posterior. -
P(D|h): a probabilidade de dadosd, considerando que a hipótesehera verdadeira. Isso é conhecido como probabilidade posterior.
O fluxo de trabalho da classificação Naive Bayes
Sempre que você fizer uma classificação, o primeiro passo é entender o problema e identificar possíveis características e rótulos. Características são aquelas coisas que afetam os resultados da etiqueta. Por exemplo, quando alguém quer um empréstimo, os gerentes do banco olham a profissão, renda, idade, onde mora, histórico de empréstimos anteriores, histórico de transações e pontuação de crédito do cliente. Essas características são conhecidas como recursos que ajudam o modelo a classificar os clientes.
A classificação tem duas fases: uma fase de aprendizagem e uma fase de avaliação. Na fase de aprendizagem, o classificador treina seu modelo em um determinado conjunto de dados e, na fase de avaliação, testa o desempenho do classificador. O desempenho é avaliado com base em vários parâmetros, como exatidão, erro, precisão e recuperação.
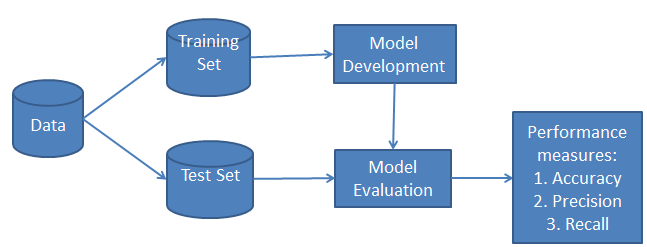
Como funciona o classificador Naive Bayes?
Vamos entender como funciona o Naive Bayes com um exemplo. Dando um exemplo de condições climáticas e prática de esportes. Você precisa calcular a probabilidade de praticar esportes. Agora, você precisa decidir se os jogadores vão jogar ou não, dependendo do tempo.
Primeira abordagem (no caso de uma única característica)
O classificador Naive Bayes calcula a probabilidade de um evento nas seguintes etapas:
- Passo 1: Calcule a probabilidade a priori para determinados rótulos de classe.
- Passo 2: Descubra a probabilidade de cada atributo para cada classe.
- Passo 3: Coloque esses valores na Fórmula de Bayes e calcule a probabilidade posterior.
- Passo 4: Veja qual classe tem maior probabilidade, já que a entrada pertence à classe de maior probabilidade.
Para simplificar o cálculo da probabilidade a priori e a posteriori, você pode usar as duas tabelas: tabela de frequência e tabela de verossimilhança. Essas duas tabelas vão te ajudar a calcular a probabilidade a priori e a posteriori. A tabela de frequência mostra quantas vezes cada rótulo aparece em todas as características. Existem duas tabelas de probabilidade. A Tabela de Probabilidade 1 mostra as probabilidades a priori dos rótulos e a Tabela de Probabilidade 2 mostra a probabilidade a posteriori.
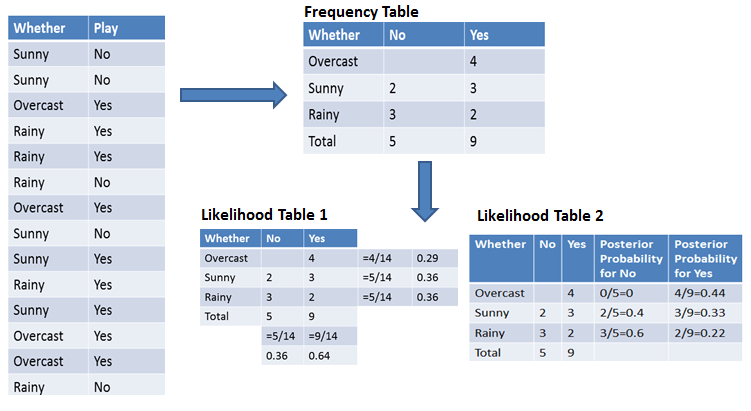
Agora, imagina que você quer calcular a probabilidade de jogar quando o tempo está nublado.
Probabilidade de jogar:
P(Sim | Nublado) = P(Nublado | Sim) × P(Sim) / P(Nublado)
Passo 1: Calcular probabilidades prévias
- P(Nublado) = 4/14 = 0,29
- P(Sim) = 9/14 = 0,64
Passo 2: Calcular a probabilidade posterior
- P(Nublado | Sim) = 4/9 = 0,44
Passo 3: Aplique a fórmula de Bayes
Aqui, colocamos as probabilidades a priori e a posteriori na primeira equação.
P(Sim | Nublado) = 0,44 × 0,64 / 0,29 = 0,98
Da mesma forma, você pode calcular a probabilidade de não jogar:
Probabilidade de não jogar:
P(Não | Nublado) = P(Nublado | Não) × P(Não) / P(Nublado)
Passo 1: Calcule as probabilidades a priori
- P(Nublado) = 4/14 = 0,29
- P(Não) = 5/14 = 0,36
Passo 2: Calcular a probabilidade
- P(Nublado | Não) = 0/5 = 0
Passo 3: Aplique a fórmula de Bayes
Aqui, colocamos as probabilidades a priori e de verossimilhança na equação para obter a probabilidade a posteriori.
P(Não | Nublado) = 0 × 0,36 / 0,29 = 0
A chance de uma resposta “Sim” é maior. Então, você pode ver aqui se o tempo está nublado, e aí os jogadores vão praticar o esporte.
Segunda abordagem (no caso de múltiplas características)
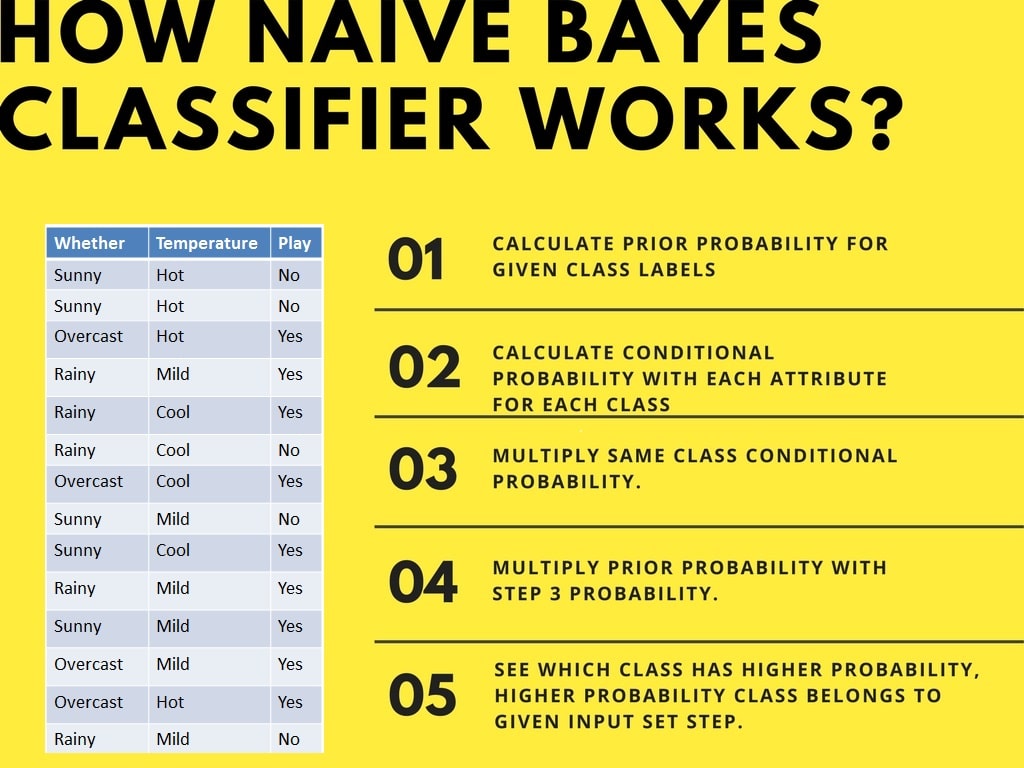
Agora, imagina que você quer calcular a probabilidade de jogar quando o tempo está nublado e a temperatura está amena.
Probabilidade de jogar:
P(Brincar = Sim | Clima = Nublado, Temperatura = Amena) = P(Clima = Nublado, Temperatura = Amena | Brincar = Sim) × P(Brincar = Sim)
Usando a suposição de independência do Naive Bayes:
P(Clima = Nublado, Temperatura = Amena | Brincar = Sim) = P(Nublado | Sim) × P(Amena | Sim)
Passo 1: Calcule a probabilidade a priori
- P(Sim) = 9/14 = 0,64
Passo 2: Calcular probabilidades
- P(Nublado | Sim) = 4/9 = 0,44
- P(Leve | Sim) = 4/9 = 0,44
Passo 3: Calcular a probabilidade combinada
P(Clima = Nublado, Temperatura = Amena | Brincar = Sim) = 0,44 × 0,44 = 0,1936
Passo 4: Aplique a fórmula de Bayes
P(Jogar = Sim | Clima = Nublado, Temperatura = Amena) = 0,1936 × 0,64 = 0,124
Da mesma forma, você pode calcular a probabilidade de não jogar:
Probabilidade de não jogar:
P(Brincar = Não | Clima = Nublado, Temperatura = Amena) = P(Clima = Nublado, Temperatura = Amena | Brincar = Não) × P(Brincar = Não)
Usando a suposição de independência do Naive Bayes:
P(Clima = Nublado, Temperatura = Amena | Brincar = Não) = P(Nublado | Não) × P(Amena | Não)
Passo 1: Calcule a probabilidade a priori
- P(Não) = 5/14 = 0,36
Passo 2: Calcular probabilidades
- P(Nublado | Não) = 0/5 = 0
- P(Leve | Não) = 2/5 = 0,4
Passo 3: Calcular a probabilidade combinada
P(Clima = Nublado, Temperatura = Amena | Brincar = Não) = 0 × 0,4 = 0
Passo 4: Aplique a fórmula de Bayes
P(Jogar = Não | Clima = Nublado, Temperatura = Amena) = 0 × 0,36 = 0
A probabilidade da classe “Sim” é maior (0,124 contra 0), então, se o tempo estiver nublado e a temperatura amena, os jogadores praticarão o esporte.
Criação de classificadores no Scikit-learn
Classificador Naive Bayes com um conjunto de dados sintéticos
No primeiro exemplo, vamos gerar dados sintéticos usando o scikit-learn e treinar e avaliar o algoritmo Gaussiano Naive Bayes.
Gerando o conjunto de dados
O Scikit-learn nos oferece um ecossistema de machine learning para que possamos gerar o conjunto de dados e avaliar vários algoritmos de machine learning.
No nosso caso, estamos criando um conjunto de dados com seis características, três classes e 800 amostras usando a função ` make_classification() `.
from sklearn.datasets import make_classification
X, y = make_classification(
n_features=6,
n_classes=3,
n_samples=800,
n_informative=2,
random_state=1,
n_clusters_per_class=1,
)Vamos usar a função scatter() do matplotlib.pyplotpara visualizar o conjunto de dados.
import matplotlib.pyplot as plt
plt.scatter(X[:, 0], X[:, 1], c=y, marker="*");Como dá pra ver, tem três tipos de rótulos de destino, e vamos treinar um modelo de classificação multiclasse.
Divisão do teste do trem
Antes de começarmos o processo de treinamento, precisamos dividir o conjunto de dados em treinamento e teste para avaliação do modelo.
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.33, random_state=125
)Construção e treinamento de modelos
Crie um modelo genérico Gaussiano Naive Bayes e treine-o em um conjunto de dados de treinamento. Depois disso, insira uma amostra de teste aleatória no modelo para obter um valor previsto.
from sklearn.naive_bayes import GaussianNB
# Build a Gaussian Classifier
model = GaussianNB()
# Model training
model.fit(X_train, y_train)
# Predict Output
predicted = model.predict([X_test[6]])
print("Actual Value:", y_test[6])
print("Predicted Value:", predicted[0])Os valores reais e os valores previstos são iguais.
Actual Value: 0
Predicted Value: 0Avaliação do modelo
Não vamos desenvolver o modelo em um conjunto de dados de teste não visto. Primeiro, vamos prever os valores para o conjunto de dados de teste e usá-los para calcular a precisão e a pontuação F1.
from sklearn.metrics import (
accuracy_score,
confusion_matrix,
ConfusionMatrixDisplay,
f1_score,
)
y_pred = model.predict(X_test)
accuray = accuracy_score(y_pred, y_test)
f1 = f1_score(y_pred, y_test, average="weighted")
print("Accuracy:", accuray)
print("F1 Score:", f1)Nosso modelo tem funcionado bem com os hiperparâmetros padrão.
Accuracy: 0.8484848484848485
F1 Score: 0.8491119695890328Para visualizar a matriz de confusão, vamos usar confusion_matrix para calcular os verdadeiros positivos e os verdadeiros negativos e ConfusionMatrixDisplaypara mostrar a matriz de confusão com os rótulos.
labels = [0,1,2]
cm = confusion_matrix(y_test, y_pred, labels=labels)
disp = ConfusionMatrixDisplay(confusion_matrix=cm, display_labels=labels)
disp.plot();Nosso modelo tem funcionado muito bem, e podemos melhorar o desempenho do modelo por meio de dimensionamento, pré-processamento de validações cruzadas e otimização de hiperparâmetros.
Classificador Naive Bayes com um conjunto de dados de empréstimos
Vamos treinar o Classificador Naive Bayes com o conjunto de dados reais. Vamos repetir a maioria das tarefas, exceto o pré-processamento e a exploração de dados.
Carregamento de dados
Neste exemplo, vamos carregar os dados de empréstimos do DataLab usando a função read_csvdo pandas.
import pandas as pd
df = pd.read_csv('loan_data.csv')
df.head()Exploração de dados
Para entender melhor o conjunto de dados, vamos usar .info().
-
O conjunto de dados tem 14 colunas e 9578 linhas.
-
Além de
purpose, as colunas são flutuantes ou inteiras. -
A nossa coluna alvo é
not.fully.paid.
df.info()RangeIndex: 9578 entries, 0 to 9577
Data columns (total 14 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 credit.policy 9578 non-null int64
1 purpose 9578 non-null object
2 int.rate 9578 non-null float64
3 installment 9578 non-null float64
4 log.annual.inc 9578 non-null float64
5 dti 9578 non-null float64
6 fico 9578 non-null int64
7 days.with.cr.line 9578 non-null float64
8 revol.bal 9578 non-null int64
9 revol.util 9578 non-null float64
10 inq.last.6mths 9578 non-null int64
11 delinq.2yrs 9578 non-null int64
12 pub.rec 9578 non-null int64
13 not.fully.paid 9578 non-null int64
dtypes: float64(6), int64(7), object(1)
memory usage: 1.0+ MBNeste exemplo, vamos desenvolver um modelo para prever quais clientes não pagaram totalmente o empréstimo. Vamos dar uma olhada na coluna de propósito e alvo usando o countplot do seaborn.
import seaborn as sns
import matplotlib.pyplot as plt
sns.countplot(data=df,x='purpose',hue='not.fully.paid')
plt.xticks(rotation=45, ha='right');Nosso conjunto de dados tem um desequilíbrio que vai afetar o desempenho do modelo. Você pode conferir o tutorial Reamostrar um conjunto de dados desequilibrado para ter uma experiência prática no manuseio de conjuntos de dados desequilibrados.
Processamento de dados
Agora vamos converter a coluna “ purpose ” de categórica para inteira usando a função “ get_dummies() ” do pandas.
pre_df = pd.get_dummies(df,columns=['purpose'],drop_first=True)
pre_df.head()Depois disso, vamos definir as variáveis de característica (X) e alvo (y) e dividir o conjunto de dados em conjuntos de treinamento e teste.
from sklearn.model_selection import train_test_split
X = pre_df.drop('not.fully.paid', axis=1)
y = pre_df['not.fully.paid']
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.33, random_state=125
)Construção e treinamento de modelos
A criação e o treinamento do modelo são bem simples. Vamos treinar um modelo em um conjunto de dados de treinamento usando hiperparâmetros padrão.
from sklearn.naive_bayes import GaussianNB
model = GaussianNB()
model.fit(X_train, y_train);Avaliação do modelo
Vamos usar a precisão e a pontuação f1 para ver como o modelo se saiu, e parece que o algoritmo Gaussiano Naive Bayes se saiu bem.
from sklearn.metrics import (
accuracy_score,
confusion_matrix,
ConfusionMatrixDisplay,
f1_score,
classification_report,
)
y_pred = model.predict(X_test)
accuray = accuracy_score(y_pred, y_test)
f1 = f1_score(y_pred, y_test, average="weighted")
print("Accuracy:", accuray)
print("F1 Score:", f1)Accuracy: 0.8206263840556786
F1 Score: 0.8686606980013266Por causa da natureza desequilibrada dos dados, dá pra ver que a matriz de confusão conta uma história diferente. Em um alvo minoritário: not fully paid, temos mais erros de rotulagem.
labels = ["Fully Paid", "Not fully Paid"]
cm = confusion_matrix(y_test, y_pred)
disp = ConfusionMatrixDisplay(confusion_matrix=cm, display_labels=labels)
disp.plot();Se você estiver enfrentando problemas durante o treinamento ou a avaliação do modelo, pode conferir o Tutorial de Classificação Naive Bayes usando a pasta de trabalho Scikit-learn DataLab. Ele vem com um conjunto de dados, código-fonte e resultados.
Problema de Probabilidade Zero
Digamos que não tem nenhum tuplo para um empréstimo arriscado no conjunto de dados; nesse caso, a probabilidade posterior vai ser zero, e o modelo não vai conseguir fazer uma previsão. Esse problema é conhecido como Probabilidade Zero porque a ocorrência dessa classe específica é zero.
A solução para esse problema é a correção laplaciana ou transformação de Laplace. A correção laplaciana é uma das técnicas de suavização. Aqui, você pode supor que o conjunto de dados é grande o suficiente para que adicionar uma linha de cada classe não faça diferença na probabilidade estimada. Isso vai resolver o problema dos valores de probabilidade para zero.
Por exemplo: Digamos que, para a classe empréstimo arriscado, tem 1000 tuplas de treinamento no banco de dados. Nesse banco de dados, a coluna de renda tem 0 tuplas para renda baixa, 990 tuplas para renda média e 10 tuplas para renda alta. As probabilidades desses eventos, sem a correção laplaciana, são 0, 0,990 (de 990/1000) e 0,010 (de 10/1000).
Agora, aplique a correção laplaciana no conjunto de dados fornecido. Vamos adicionar mais 1 tupla para cada par de valores de renda. As chances desses eventos acontecerem:
Vantagens do Naive Bayes
- Não é só uma abordagem simples, mas também um jeito rápido e preciso de fazer previsões.
- O Naive Bayes tem um custo de computação bem baixo.
- Ele consegue trabalhar bem com um monte de dados.
- Tem um bom desempenho no caso de variáveis de resposta discretas em comparação com variáveis contínuas.
- Pode ser usado com vários problemas de previsão de classe.
- Ele também funciona bem quando se trata de problemas de análise de texto.
- Quando a suposição de independência se mantém, um classificador Naive Bayes tem um desempenho melhor em comparação com outros modelos, como a regressão logística.
Desvantagens do Naive Bayes
- A ideia de características independentes. Na prática, é quase impossível que o modelo obtenha um conjunto de preditores que sejam totalmente independentes.
- Se não tiver um conjunto de dados de treino de uma determinada classe, isso vai causar uma probabilidade posterior zero. Nesse caso, o modelo não consegue fazer previsões. Esse problema é conhecido como Problema de Probabilidade/Frequência Zero.
Conclusão
Parabéns, você chegou ao fim deste tutorial!
Neste tutorial, você aprendeu sobre o algoritmo Naive Bayes, como ele funciona, as premissas do Naive Bayes, os problemas, a implementação, as vantagens e as desvantagens. Ao longo do caminho, você também aprendeu a construir e avaliar modelos no scikit-learn para classes binárias e multinomiais.
O Naive Bayes é o algoritmo mais simples e potente. Apesar dos avanços significativos no machine learning nos últimos anos, ele provou seu valor. Ele foi implementado com sucesso em várias aplicações, desde análise de texto até mecanismos de recomendação.
Se você quiser saber mais sobre o scikit-learn em Python, faça nosso curso Aprendizado supervisionado com scikit-learn e confira nosso Tutorial Scikit-Learn : Análise do beisebol, parte 1.
Tópicos
