Tutorial zur Naive-Bayes-Klassifizierung mit Scikit-learn

Was ist der Naive-Bayes-Klassifikator?

Naive Bayes ist eine statistische Klassifizierungstechnik, die auf dem Bayes-Theorem basiert. Es ist einer der einfachsten Algorithmen für überwachtes Lernen. Der Naive-Bayes-Klassifikator ist ein schneller, genauer und zuverlässiger Algorithmus. Naive Bayes-Klassifikatoren sind bei großen Datensätzen echt genau und schnell.

Der Naive-Bayes-Klassifikator geht davon aus, dass der Einfluss eines bestimmten Merkmals in einer Klasse unabhängig von anderen Merkmalen ist. Zum Beispiel hängt es von deinem Einkommen, früheren Krediten und Transaktionen, deinem Alter und deinem Wohnort ab, ob du für einen Kredit in Frage kommst oder nicht. Auch wenn diese Funktionen voneinander abhängen, werden sie trotzdem unabhängig voneinander betrachtet. Diese Annahme macht die Berechnung einfacher, und deshalb wird sie als naiv angesehen. Diese Annahme wird als klassenbedingte Unabhängigkeit bezeichnet.

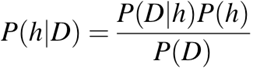
• P(h)Die Wahrscheinlichkeit, dass die Hypothese h stimmt (egal, was die Daten sagen). Das nennt man die A-priori-Wahrscheinlichkeit von h.

• P(D)Die Wahrscheinlichkeit der Daten (egal, was man denkt). Das nennt man die A-priori-Wahrscheinlichkeit.

• P(h|D)Die Wahrscheinlichkeit der Hypothese h, wenn man die Daten D hat. Das nennt man die A-posteriori-Wahrscheinlichkeit.

• P(D|h)Die Wahrscheinlichkeit, dass die Daten d, wenn die Hypothese h stimmt. Das nennt man die A-posteriori-Wahrscheinlichkeit.

Der Naive-Bayes-Klassifizierungs-Workflow

Wenn du eine Klassifizierung machst, musst du zuerst das Problem verstehen und mögliche Merkmale und Bezeichnungen herausfinden. Eigenschaften sind die Merkmale oder Attribute, die die Ergebnisse des Labels beeinflussen. Bei der Vergabe von Krediten checken Bankmanager zum Beispiel den Job, das Einkommen, das Alter, den Wohnort, die bisherigen Kredite, die Transaktionshistorie und die Bonität des Kunden. Diese Eigenschaften sind als Merkmale bekannt, die dem Modell helfen, Kunden zu klassifizieren.

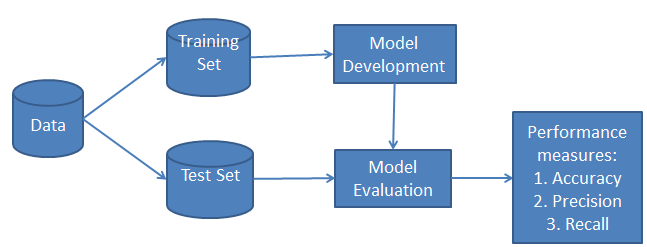
Die Klassifizierung hat zwei Phasen: eine Lernphase und eine Bewertungsphase. In der Lernphase trainiert der Klassifikator sein Modell anhand eines bestimmten Datensatzes, und in der Bewertungsphase testet er die Leistung des Klassifikators. Die Leistung wird anhand von verschiedenen Parametern wie Genauigkeit, Fehlerquote, Präzision und Wiederauffindbarkeit bewertet.

Wie funktioniert der Naive-Bayes-Klassifikator?

Schauen wir uns mal anhand eines Beispiels an, wie Naive Bayes funktioniert. Nimm mal das Beispiel Wetterbedingungen und Sport treiben. Du musst die Wahrscheinlichkeit berechnen, mit der du Sport treibst. Jetzt musst du anhand der Wetterbedingungen entscheiden, ob die Spieler spielen werden oder nicht.

Erster Ansatz (wenn es nur ein Merkmal gibt)

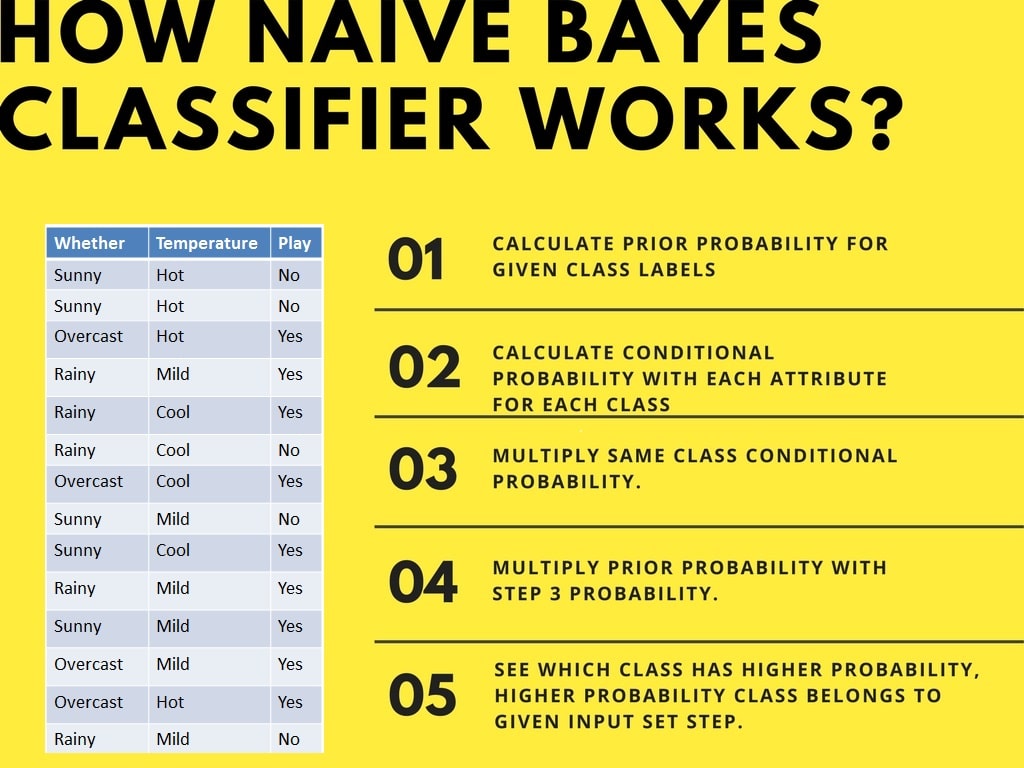
Der Naive-Bayes-Klassifikator berechnet die Wahrscheinlichkeit eines Ereignisses in folgenden Schritten:

• Schritt 1: Berechne die A-priori-Wahrscheinlichkeit für bestimmte Klassenbezeichnungen.
• Schritt 2: Finde die Wahrscheinlichkeit für jedes Attribut für jede Klasse.
• Schritt 3: Gib diese Werte in die Bayes-Formel ein und berechne die a-posteriori-Wahrscheinlichkeit.
• Schritt 4: Schau mal, welche Klasse eine höhere Wahrscheinlichkeit hat, wenn die Eingabe zur Klasse mit der höheren Wahrscheinlichkeit gehört.

Um die Berechnung der A-priori- und A-posteriori-Wahrscheinlichkeit zu vereinfachen, kannst du die beiden Tabellen Häufigkeitstabelle und Wahrscheinlichkeitstabelle nutzen. Beide Tabellen helfen dir dabei, die a-priori- und a-posteriori-Wahrscheinlichkeit zu berechnen. Die Häufigkeitstabelle zeigt, wie oft die Bezeichnungen für alle Merkmale vorkommen. Es gibt zwei Wahrscheinlichkeitstabellen. Die Wahrscheinlichkeitstabelle 1 zeigt die vorherigen Wahrscheinlichkeiten der Labels und die Wahrscheinlichkeitstabelle 2 zeigt die nachherigen Wahrscheinlichkeiten.

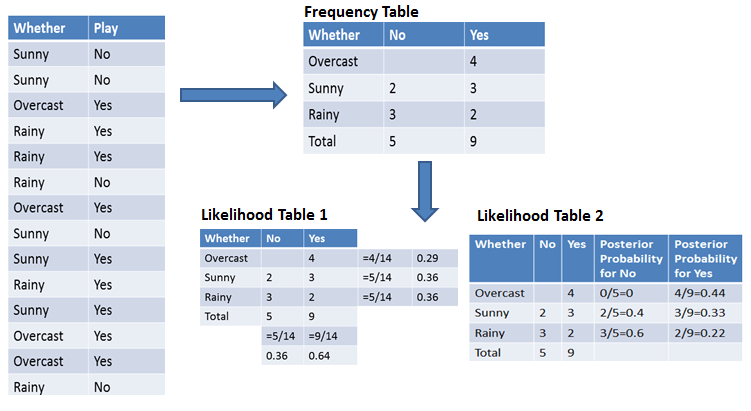
Angenommen, du willst die Wahrscheinlichkeit berechnen, mit der du bei bewölktem Wetter spielst.

Wahrscheinlichkeit, dass ich mitspiele:

P(Ja | Bewölkt) = P(Bewölkt | Ja) × P(Ja) / P(Bewölkt)

Schritt 1: Berechne die Vorherwahrscheinlichkeiten

• P(Bewölkt) = 4/14 = 0,29
• P(Ja) = 9/14 = 0,64

Schritt 2: Berechne die a-posteriori-Wahrscheinlichkeit.

• P(Bewölkt | Ja) = 4/9 = 0,44

Schritt 3: Wende die Bayes-Formel an. 

Hier setzen wir die A-priori- und A-posteriori-Wahrscheinlichkeiten in die erste Gleichung ein.

P(Ja | Bewölkt) = 0,44 × 0,64 / 0,29 = 0,98

Genauso kannst du die Wahrscheinlichkeit berechnen, nicht zu spielen:

Wahrscheinlichkeit, nicht zu spielen:

P(Nein | Bewölkt) = P(Bewölkt | Nein) × P(Nein) / P(Bewölkt)

Schritt 1: Berechne die A-priori-Wahrscheinlichkeiten.

• P(Bewölkt) = 4/14 = 0,29
• P(Nein) = 5/14 = 0,36

Schritt 2: Wahrscheinlichkeit berechnen

• P(Bewölkt | Nein) = 0/5 = 0

Schritt 3: Wende die Bayes-Formel an.

Hier setzen wir die A-priori- und Wahrscheinlichkeitswahrscheinlichkeiten in die Gleichung ein, um die A-posteriori-Wahrscheinlichkeit zu bekommen.

P(Nein | Bewölkt) = 0 × 0,36 / 0,29 = 0

Die Wahrscheinlichkeit für eine „Ja“-Klasse ist höher. Du kannst hier also festlegen, ob bei bewölktem Wetter die Spieler den Sport ausüben werden.

Zweiter Ansatz (wenn es mehrere Merkmale gibt)

Angenommen, du willst die Wahrscheinlichkeit berechnen, mit der du bei bewölktem Wetter und milden Temperaturen spielen gehst.

Wahrscheinlichkeit, dass ich mitspiele:

P(Spielen = Ja | Wetter = bewölkt, Temperatur = mild) = P(Wetter = bewölkt, Temperatur = mild | Spielen = Ja) × P(Spielen = Ja)

Mit der Naive-Bayes-Unabhängigkeitsannahme:

P(Wetter = bewölkt, Temperatur = mild | Spielen = Ja) = P(bewölkt | Ja) × P(mild | Ja)

Schritt 1: Berechne die A-priori-Wahrscheinlichkeit

• P(Ja) = 9/14 = 0,64

Schritt 2: Wahrscheinlichkeiten berechnen

• P(Bewölkt | Ja) = 4/9 = 0,44
• P(Mild | Ja) = 4/9 = 0,44

Schritt 3: Kombinierte Wahrscheinlichkeit berechnen

P(Wetter = bewölkt, Temperatur = mild | Spielen = Ja) = 0,44 × 0,44 = 0,1936

Schritt 4: Wende die Bayes-Formel an.

P(Spiel = Ja | Wetter = bewölkt, Temperatur = mild) = 0,1936 × 0,64 = 0,124

Genauso kannst du die Wahrscheinlichkeit berechnen, nicht zu spielen:

Wahrscheinlichkeit, nicht zu spielen:

P(Spielen = Nein | Wetter = Bewölkt, Temperatur = Mild) = P(Wetter = Bewölkt, Temperatur = Mild | Spielen = Nein) × P(Spielen = Nein)

Mit der Naive-Bayes-Unabhängigkeitsannahme:

P(Wetter = bewölkt, Temperatur = mild | Spielen = Nein) = P(bewölkt | Nein) × P(mild | Nein)

Schritt 1: Berechne die A-priori-Wahrscheinlichkeit

• P(Nein) = 5/14 = 0,36

Schritt 2: Wahrscheinlichkeiten berechnen

• P(Bewölkt | Nein) = 0/5 = 0
• P(leicht | nein) = 2/5 = 0,4

Schritt 3: Kombinierte Wahrscheinlichkeit berechnen

P(Wetter = bewölkt, Temperatur = mild | Spielen = nein) = 0 × 0,4 = 0

Schritt 4: Wende die Bayes-Formel an.

P(Spiel = Nein | Wetter = bewölkt, Temperatur = mild) = 0 × 0,36 = 0

Die Wahrscheinlichkeit für die Klasse „Ja“ ist höher (0,124 gegenüber 0), also wenn das Wetter bewölkt und die Temperatur mild ist, werden die Spieler den Sport ausüben.

Klassifikatorerstellung in Scikit-learn

Naiver Bayes-Klassifikator mit einem synthetischen Datensatz

Im ersten Beispiel machen wir künstliche Daten mit scikit-learn und trainieren und checken den Gaußschen Naive-Bayes-Algorithmus. 

Erstellen des Datensatzes

Scikit-learn gibt uns ein Machine-Learning-Ökosystem, mit dem wir den Datensatz erstellen und verschiedene Machine-Learning-Algorithmen ausprobieren können. 

In unserem Fall erstellen wir mit der Funktion „ make_classification() “ einen Datensatz mit sechs Merkmalen, drei Klassen und 800 Beispielen. 

from sklearn.datasets import make_classification

X, y = make_classification(
    n_features=6,
    n_classes=3,
    n_samples=800,
    n_informative=2,
    random_state=1,
    n_clusters_per_class=1,
)

Wir werden die Funktion „ scatter() ” von matplotlib.pyplotnutzen, um den Datensatz zu zeigen. 

import matplotlib.pyplot as plt

plt.scatter(X[:, 0], X[:, 1], c=y, marker="*");

Wie wir sehen können, gibt es drei Arten von Zielbezeichnungen, und wir werden ein Multiklassen-Klassifizierungsmodell trainieren. 

Zugtest-Aufteilung

Bevor wir mit dem Trainingsprozess anfangen, müssen wir den Datensatz für die Modellbewertung in Trainings- und Testdaten aufteilen. 

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.33, random_state=125
)

Modellbau und Training 

Mach ein generisches Gaußsches Naive-Bayes-Modell und trainiere es mit einem Trainingsdatensatz. Danach gibst du eine zufällige Testprobe ins Modell rein, um einen vorhergesagten Wert zu kriegen.

from sklearn.naive_bayes import GaussianNB

# Build a Gaussian Classifier
model = GaussianNB()

# Model training
model.fit(X_train, y_train)

# Predict Output
predicted = model.predict([X_test[6]])

print("Actual Value:", y_test[6])
print("Predicted Value:", predicted[0])

Die tatsächlichen und die vorhergesagten Werte sind gleich. 

Actual Value: 0
Predicted Value: 0

Modellbewertung

Wir werden das Modell nicht anhand eines unbekannten Testdatensatzes weiterentwickeln. Zuerst werden wir die Werte für den Testdatensatz vorhersagen und sie nutzen, um die Genauigkeit und den F1-Score zu berechnen. 

from sklearn.metrics import (
    accuracy_score,
    confusion_matrix,
    ConfusionMatrixDisplay,
    f1_score,
)

y_pred = model.predict(X_test)
accuray = accuracy_score(y_pred, y_test)
f1 = f1_score(y_pred, y_test, average="weighted")

print("Accuracy:", accuray)
print("F1 Score:", f1)

Unser Modell hat mit den Standard-Hyperparametern ziemlich gut funktioniert. 

Accuracy: 0.8484848484848485
F1 Score: 0.8491119695890328

Um die Verwechslungsmatrix zu zeigen, benutzen wir confusion_matrix, um die echten Positiven und echten Negativen zu berechnen, und ConfusionMatrixDisplay, um die Verwechslungsmatrix mit den Beschriftungen anzuzeigen.

labels = [0,1,2]
cm = confusion_matrix(y_test, y_pred, labels=labels)
disp = ConfusionMatrixDisplay(confusion_matrix=cm, display_labels=labels)
disp.plot();

Unser Modell hat echt gut funktioniert, und wir können die Leistung noch verbessern, indem wir es skalieren, Kreuzvalidierungen vorverarbeiten und die Hyperparameter optimieren. 

Naiver Bayes-Klassifikator mit einem Kredit-Datensatz

Lass uns den Naive-Bayes-Klassifikator mit dem echten Datensatz trainieren. Wir werden die meisten Aufgaben wiederholen, außer der Vorverarbeitung und der Datenauswertung. 

Daten laden

In diesem Beispiel laden wir Kreditdaten aus DataLab mit der Funktion „read_csv”von pandas. 

import pandas as pd


df = pd.read_csv('loan_data.csv')
df.head()

Datenauswertung

Um mehr über den Datensatz zu erfahren, schauen wir uns .info() an.

• Der Datensatz hat 14 Spalten und 9578 Zeilen.

• Außer „ purpose “ sind die Spalten entweder Fließkommazahlen oder Ganzzahlen. 

• Unsere Zielspalte ist „ not.fully.paid “. 

df.info()

RangeIndex: 9578 entries, 0 to 9577
Data columns (total 14 columns):
#   Column             Non-Null Count  Dtype 
---  ------             --------------  ----- 
0   credit.policy      9578 non-null   int64 
1   purpose            9578 non-null   object
2   int.rate           9578 non-null   float64
3   installment        9578 non-null   float64
4   log.annual.inc     9578 non-null   float64
5   dti                9578 non-null   float64
6   fico               9578 non-null   int64 
7   days.with.cr.line  9578 non-null   float64
8   revol.bal          9578 non-null   int64 
9   revol.util         9578 non-null   float64
10  inq.last.6mths     9578 non-null   int64 
11  delinq.2yrs        9578 non-null   int64 
12  pub.rec            9578 non-null   int64 
13  not.fully.paid     9578 non-null   int64 
dtypes: float64(6), int64(7), object(1)
memory usage: 1.0+ MB

In diesem Beispiel entwickeln wir ein Modell, um vorherzusagen, welche Kunden ihren Kredit nicht komplett zurückgezahlt haben. Schauen wir uns mal die Spalten „Zweck“ und „Zielgruppe“ mit dem Countplot von Seaborn an. 

import seaborn as sns
import matplotlib.pyplot as plt

sns.countplot(data=df,x='purpose',hue='not.fully.paid')
plt.xticks(rotation=45, ha='right');

Unser Datensatz ist unausgewogen, was die Leistung des Modells beeinträchtigen wird. Schau dir das Tutorial „Resample an Imbalanced Dataset” an, um praktische Erfahrungen im Umgang mit unausgewogenen Datensätzen zu sammeln.

Datenverarbeitung 

Jetzt wandeln wir die Spalte „ purpose ” mit der pandas-Funktion „ get_dummies() ” von einer kategorialen in eine ganzzahlige Spalte um.

pre_df = pd.get_dummies(df,columns=['purpose'],drop_first=True)
pre_df.head()

Danach legen wir die Merkmals- (X) und Zielvariablen (y) fest und teilen den Datensatz in Trainings- und Testdatensätze auf. 

from sklearn.model_selection import train_test_split

X = pre_df.drop('not.fully.paid', axis=1)
y = pre_df['not.fully.paid']

X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.33, random_state=125
)

Modellbau und Training

Das Erstellen und Trainieren von Modellen ist echt einfach. Wir trainieren ein Modell auf einem Trainingsdatensatz mit den Standard-Hyperparametern. 

from sklearn.naive_bayes import GaussianNB

model = GaussianNB()

model.fit(X_train, y_train);

Modellbewertung

Wir werden die Genauigkeit und den F1-Score nutzen, um die Modellleistung zu checken, und es sieht so aus, als hätte der Gaußsche Naive-Bayes-Algorithmus ziemlich gut abgeschnitten. 

from sklearn.metrics import (
    accuracy_score,
    confusion_matrix,
    ConfusionMatrixDisplay,
    f1_score,
    classification_report,
)

y_pred = model.predict(X_test)

accuray = accuracy_score(y_pred, y_test)
f1 = f1_score(y_pred, y_test, average="weighted")

print("Accuracy:", accuray)
print("F1 Score:", f1)

Accuracy: 0.8206263840556786
F1 Score: 0.8686606980013266

Weil die Daten unausgewogen sind, sehen wir, dass die Verwechslungsmatrix ein anderes Bild zeigt. Bei einem Minderheitenziel: not fully paid haben wir mehr falsche Beschriftungen. 

labels = ["Fully Paid", "Not fully Paid"]
cm = confusion_matrix(y_test, y_pred)
disp = ConfusionMatrixDisplay(confusion_matrix=cm, display_labels=labels)
disp.plot();

Wenn du beim Training oder bei der Modellbewertung Probleme hast, kannst du dir das Tutorial zur Naive-Bayes-Klassifizierung mit der Scikit-learn DataLab-Arbeitsmappe ansehen. Es kommt mit einem Datensatz, Quellcode und Ausgaben. 

Nullwahrscheinlichkeitsproblem

Angenommen, es gibt keinen Tupel für einen risikobehafteten Kredit im Datensatz; in diesem Fall ist die a-posteriori-Wahrscheinlichkeit gleich Null, und das Modell kann keine Vorhersage treffen. Dieses Problem wird als Nullwahrscheinlichkeit bezeichnet, weil das Auftreten der bestimmten Klasse gleich Null ist.

Die Lösung für so ein Problem ist die Laplace-Korrektur oder Laplace-Transformation. Die Laplace-Korrektur ist eine der Glättungstechniken. Hier kannst du davon ausgehen, dass der Datensatz groß genug ist, sodass das Hinzufügen einer Zeile pro Klasse keinen Unterschied bei der geschätzten Wahrscheinlichkeit macht. Damit wird das Problem der Wahrscheinlichkeitswerte von Null gelöst.

Zum Beispiel: Angenommen, für die Klasse „riskanter Kredit“ gibt es 1000 Trainingstupel in der Datenbank. In dieser Datenbank hat die Spalte „Einkommen“ 0 Tupel für niedriges Einkommen, 990 Tupel für mittleres Einkommen und 10 Tupel für hohes Einkommen. Die Wahrscheinlichkeiten für diese Ereignisse ohne Laplace-Korrektur sind 0, 0,990 (von 990/1000) und 0,010 (von 10/1000).

Jetzt mach die Laplace-Korrektur auf den gegebenen Datensatz. Fügen wir für jedes Einkommens-Wert-Paar noch ein weiteres Tupel hinzu. Die Wahrscheinlichkeiten dieser Ereignisse:

Vorteile von Naive Bayes

• Es ist nicht nur ein einfacher Ansatz, sondern auch eine schnelle und genaue Methode zur Vorhersage.
• Naive Bayes hat echt geringe Rechenkosten.
• Es kann große Datensätze echt gut verarbeiten.
• Es funktioniert gut bei diskreten Antwortvariablen im Vergleich zu kontinuierlichen Variablen.
• Es kann bei Problemen mit mehreren Klassenvorhersagen verwendet werden.
• Es funktioniert auch super bei Textanalyse-Problemen.
• Wenn die Annahme der Unabhängigkeit stimmt, ist ein Naive-Bayes-Klassifikator besser als andere Modelle wie die logistische Regression.

Nachteile von Naive Bayes

• Die Annahme unabhängiger Merkmale. In der Praxis ist es echt unwahrscheinlich, dass das Modell eine Reihe von Prädiktoren bekommt, die komplett unabhängig voneinander sind.
• Wenn es für eine bestimmte Klasse kein Trainingstupel gibt, führt das zu einer posterioren Wahrscheinlichkeit von Null. In diesem Fall kann das Modell keine Vorhersagen treffen. Dieses Problem wird als Nullwahrscheinlichkeits-/Nullhäufigkeitsproblem bezeichnet.

Fazit

Herzlichen Glückwunsch, du hast es bis zum Ende dieses Tutorials geschafft!

In diesem Tutorial hast du den Naive-Bayes-Algorithmus kennengelernt, wie er funktioniert, die Naive-Bayes-Annahme, Probleme, die Umsetzung, Vorteile und Nachteile. Unterwegs hast du auch gelernt, wie man in scikit-learn Modelle für binäre und multinomiale Klassen baut und bewertet.

Naive Bayes ist der einfachste und leistungsfähigste Algorithmus. Trotz der großen Fortschritte beim maschinellen Lernen in den letzten Jahren hat es sich echt bewährt. Es wurde schon in vielen Bereichen erfolgreich eingesetzt, von der Textanalyse bis hin zu Empfehlungssystemen.

Wenn du mehr über scikit-learn in Python erfahren möchtest, mach doch unseren Kurs „Supervised Learning with scikit-learn” und schau dir unser Tutorial „ ” an. Baseball-Analytik Teil 1.