Tutorial sobre clasificación bayesiana ingenua con Scikit-learn

¿Qué es el clasificador Naive Bayes?

Naive Bayes es una técnica de clasificación estadística basada en el teorema de Bayes. Es uno de los algoritmos de aprendizaje supervisado más sencillos. El clasificador Naive Bayes es un algoritmo rápido, preciso y fiable. Los clasificadores Naive Bayes tienen una gran precisión y velocidad en conjuntos de datos de gran tamaño.

El clasificador Naive Bayes asume que el efecto de una característica concreta en una clase es independiente de otras características. Por ejemplo, un solicitante de préstamo es deseable o no en función de tus ingresos, tu historial crediticio y de transacciones, tu edad y tu ubicación. Aunque estas características sean interdependientes, se siguen considerando de forma independiente. Esta suposición simplifica el cálculo, y por eso se considera ingenua. Esta suposición se denomina independencia condicional de clase.

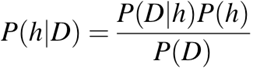
• P(h): la probabilidad de que la hipótesis h sea cierta (independientemente de los datos). Esto se conoce como probabilidad a priori de h.

• P(D): la probabilidad de los datos (independientemente de la hipótesis). Esto se conoce como probabilidad a priori.

• P(h|D): la probabilidad de la hipótesis h dados los datos D. Esto se conoce como probabilidad a posteriori.

• P(D|h): la probabilidad de que los datos d sean verdaderos, dado que la hipótesis h era cierta. Esto se conoce como probabilidad a posteriori.

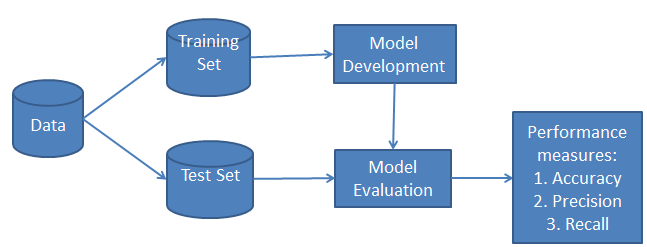
El flujo de trabajo de clasificación de Naive Bayes

Siempre que realices una clasificación, el primer paso es comprender el problema e identificar las características y etiquetas potenciales. Las características son aquellos atributos o rasgos que influyen en los resultados de la etiqueta. Por ejemplo, en el caso de la concesión de un préstamo, los directores de los bancos identifican la ocupación, los ingresos, la edad, la ubicación, el historial crediticio, el historial de transacciones y la puntuación crediticia del cliente. Estas características se conocen como rasgos que ayudan al modelo a clasificar a los clientes.

La clasificación tiene dos fases: una fase de aprendizaje y una fase de evaluación. En la fase de aprendizaje, el clasificador entrena su modelo con un conjunto de datos determinado y, en la fase de evaluación, comprueba su rendimiento. El rendimiento se evalúa en función de diversos parámetros, como la exactitud, el error, la precisión y la recuperación.

¿Cómo funciona el clasificador Naive Bayes?

Entendamos el funcionamiento de Naive Bayes mediante un ejemplo. Por ejemplo, las condiciones meteorológicas y la práctica de deportes. Debes calcular la probabilidad de practicar deporte. Ahora, debes clasificar si los jugadores jugarán o no, en función de las condiciones meteorológicas.

Primer enfoque (en caso de una sola característica)

El clasificador Naive Bayes calcula la probabilidad de un evento siguiendo estos pasos:

• Paso 1: Calcula la probabilidad a priori para las etiquetas de clase dadas.
• Paso 2: Encuentra la probabilidad de cada atributo para cada clase.
• Paso 3: Pon estos valores en la fórmula de Bayes y calcula la probabilidad a posteriori.
• Paso 4: Ver qué clase tiene una probabilidad más alta dado que la entrada pertenece a la clase de mayor probabilidad.

Para simplificar el cálculo de la probabilidad a priori y a posteriori, puedes utilizar las dos tablas: la tabla de frecuencias y la tabla de verosimilitudes. Ambas tablas te ayudarán a calcular la probabilidad a priori y a posteriori. La tabla de frecuencias contiene la aparición de etiquetas para todas las características. Hay dos tablas de probabilidades. La tabla de probabilidades 1 muestra las probabilidades a priori de las etiquetas y la tabla de probabilidades 2 muestra la probabilidad a posteriori.

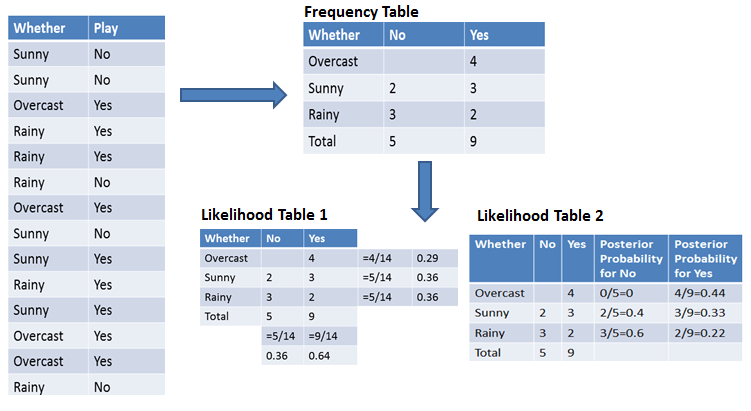
Ahora, supongamos que quieres calcular la probabilidad de jugar cuando el tiempo está nublado.

Probabilidad de jugar:

P(Sí | Nublado) = P(Nublado | Sí) × P(Sí) / P(Nublado)

Paso 1: Calcular probabilidades a priori

• P(Nublado) = 4/14 = 0,29
• P(Sí) = 9/14 = 0,64

Paso 2: Calcular la probabilidad a posteriori

• P(Nublado | Sí) = 4/9 = 0,44

Paso 3: Aplicar la fórmula de Bayes 

Aquí, ponemos las probabilidades a priori y a posteriori en la primera ecuación.

P(Sí | Nublado) = 0,44 × 0,64 / 0,29 = 0,98

Del mismo modo, puedes calcular la probabilidad de no jugar:

Probabilidad de no jugar:

P(No | Nublado) = P(Nublado | No) × P(No) / P(Nublado)

Paso 1: Calcular probabilidades a priori

• P(Nublado) = 4/14 = 0,29
• P(No) = 5/14 = 0.36

Paso 2: Calcular la probabilidad

• P(Nublado | No) = 0/5 = 0

Paso 3: Aplicar la fórmula de Bayes

Aquí, ponemos las probabilidades a priori y de verosimilitud en la ecuación para obtener la probabilidad a posteriori.

P(No | Nublado) = 0 × 0,36 / 0,29 = 0

La probabilidad de una clase «Sí» es mayor. Así que aquí puedes determinar si el tiempo está nublado, entonces los jugadores practicarán el deporte.

Segundo enfoque (en caso de múltiples características)

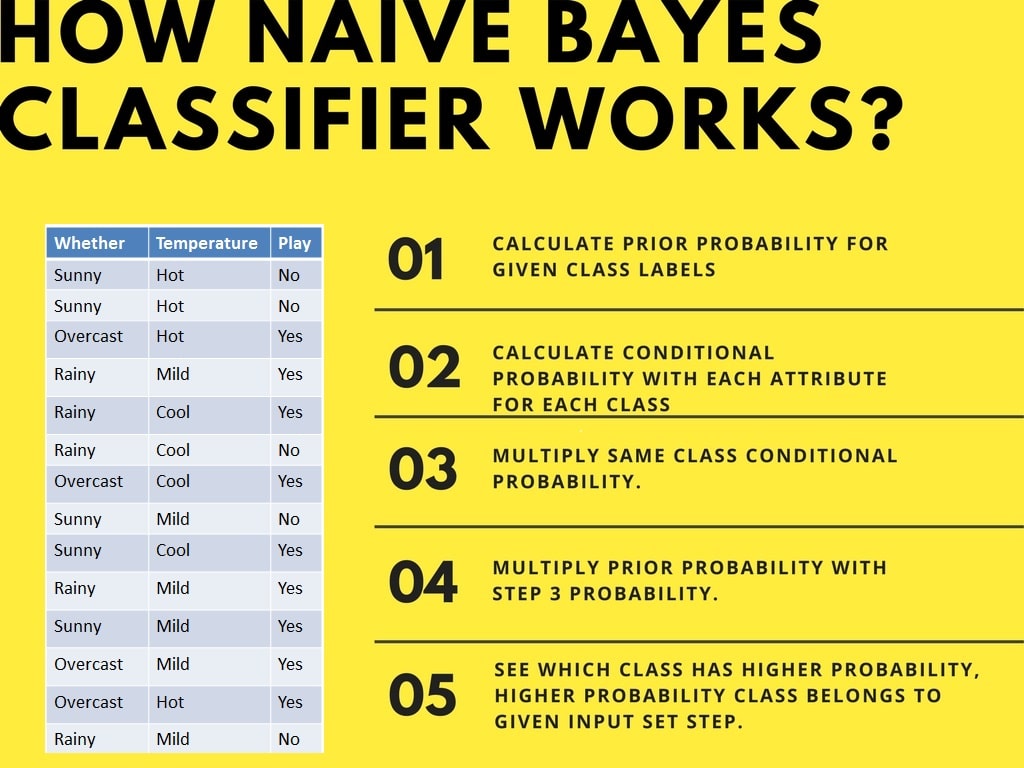
Ahora, supongamos que quieres calcular la probabilidad de jugar cuando el tiempo está nublado y la temperatura es suave.

Probabilidad de jugar:

P(Jugar = Sí | Tiempo = Nublado, Temperatura = Templada) = P(Tiempo = Nublado, Temperatura = Templada | Jugar = Sí) × P(Jugar = Sí)

Utilizando la suposición de independencia de Naive Bayes:

P(Tiempo = Nublado, Temperatura = Templada | Juego = Sí) = P(Nublado | Sí) × P(Templada | Sí)

Paso 1: Calcular la probabilidad a priori

• P(Sí) = 9/14 = 0,64

Paso 2: Calcular probabilidades

• P(Nublado | Sí) = 4/9 = 0,44
• P(Leve | Sí) = 4/9 = 0,44

Paso 3: Calcular la probabilidad combinada

P(Tiempo = Nublado, Temperatura = Templada | Juego = Sí) = 0,44 × 0,44 = 0,1936

Paso 4: Aplicar la fórmula de Bayes

P(Juego = Sí | Clima = Nublado, Temperatura = Templada) = 0,1936 × 0,64 = 0,124

Del mismo modo, puedes calcular la probabilidad de no jugar:

Probabilidad de no jugar:

P(Jugar = No | Tiempo = Nublado, Temperatura = Templada) = P(Tiempo = Nublado, Temperatura = Templada | Jugar = No) × P(Jugar = No)

Utilizando la suposición de independencia de Naive Bayes:

P(Tiempo = Nublado, Temperatura = Templada | Juego = No) = P(Nublado | No) × P(Templada | No)

Paso 1: Calcular la probabilidad a priori

• P(No) = 5/14 = 0.36

Paso 2: Calcular probabilidades

• P(Nublado | No) = 0/5 = 0
• P(Leve | No) = 2/5 = 0,4

Paso 3: Calcular la probabilidad combinada

P(Tiempo = Nublado, Temperatura = Templada | Juego = No) = 0 × 0,4 = 0

Paso 4: Aplicar la fórmula de Bayes

P(Juego = No | Clima = Nublado, Temperatura = Templada) = 0 × 0,36 = 0

La probabilidad de la clase «Sí» es mayor (0,124 frente a 0), por lo que si el tiempo está nublado y la temperatura es suave, los jugadores practicarán el deporte.

Creación de clasificadores en Scikit-learn

Clasificador Bayesiano Ingenuo con un conjunto de datos sintéticos

En el primer ejemplo, generaremos datos sintéticos utilizando scikit-learn y entrenaremos y evaluaremos el algoritmo gaussiano Naive Bayes. 

Generación del conjunto de datos

Scikit-learn nos proporciona un ecosistema de machine learning que nos permite generar el conjunto de datos y evaluar diversos algoritmos de machine learning. 

En nuestro caso, estamos creando un conjunto de datos con seis características, tres clases y 800 muestras utilizando la función « make_classification() ». 

from sklearn.datasets import make_classification

X, y = make_classification(
    n_features=6,
    n_classes=3,
    n_samples=800,
    n_informative=2,
    random_state=1,
    n_clusters_per_class=1,
)

Utilizaremos la función scatter() de matplotlib.pyplotpara visualizar el conjunto de datos. 

import matplotlib.pyplot as plt

plt.scatter(X[:, 0], X[:, 1], c=y, marker="*");

Como podemos observar, hay tres tipos de etiquetas objetivo, y entrenaremos un modelo de clasificación multiclase. 

División de pruebas de tren

Antes de comenzar el proceso de entrenamiento, necesitamos dividir el conjunto de datos en entrenamiento y prueba para la evaluación del modelo. 

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.33, random_state=125
)

Creación de modelos y formación 

Crea un modelo genérico Gaussiano Naive Bayes y entrénalo con un conjunto de datos de entrenamiento. A continuación, introduce una muestra aleatoria en el modelo para obtener un valor previsto.

from sklearn.naive_bayes import GaussianNB

# Build a Gaussian Classifier
model = GaussianNB()

# Model training
model.fit(X_train, y_train)

# Predict Output
predicted = model.predict([X_test[6]])

print("Actual Value:", y_test[6])
print("Predicted Value:", predicted[0])

Los valores reales y los valores previstos son iguales. 

Actual Value: 0
Predicted Value: 0

Evaluación del modelo

No desarrollaremos el modelo con un conjunto de datos de prueba no visto. En primer lugar, prediremos los valores para el conjunto de datos de prueba y los utilizaremos para calcular la precisión y la puntuación F1. 

from sklearn.metrics import (
    accuracy_score,
    confusion_matrix,
    ConfusionMatrixDisplay,
    f1_score,
)

y_pred = model.predict(X_test)
accuray = accuracy_score(y_pred, y_test)
f1 = f1_score(y_pred, y_test, average="weighted")

print("Accuracy:", accuray)
print("F1 Score:", f1)

Nuestro modelo ha funcionado bastante bien con los hiperparámetros predeterminados. 

Accuracy: 0.8484848484848485
F1 Score: 0.8491119695890328

Para visualizar la matriz de confusión, utilizaremos confusion_matrix para calcular los verdaderos positivos y los verdaderos negativos, y ConfusionMatrixDisplay para mostrar la matriz de confusión con las etiquetas.

labels = [0,1,2]
cm = confusion_matrix(y_test, y_pred, labels=labels)
disp = ConfusionMatrixDisplay(confusion_matrix=cm, display_labels=labels)
disp.plot();

Nuestro modelo ha funcionado bastante bien, y podemos mejorar su rendimiento mediante el escalado, el preprocesamiento de validaciones cruzadas y la optimización de hiperparámetros. 

Clasificador bayesiano ingenuo con un conjunto de datos de préstamos

Entrenemos el clasificador Naive Bayes con el conjunto de datos reales. Repetiremos la mayoría de las tareas, excepto el preprocesamiento y la exploración de datos. 

Carga de datos

En este ejemplo, cargaremos datos de préstamos desde DataLab utilizando la función read_csvde pandas. 

import pandas as pd


df = pd.read_csv('loan_data.csv')
df.head()

Exploración de datos

Para comprender mejor el conjunto de datos, utilizaremos .info().

• El conjunto de datos consta de 14 columnas y 9578 filas.

• Aparte de purpose, las columnas son flotantes o enteras. 

• Tu columna de destino es not.fully.paid. 

df.info()

RangeIndex: 9578 entries, 0 to 9577
Data columns (total 14 columns):
#   Column             Non-Null Count  Dtype 
---  ------             --------------  ----- 
0   credit.policy      9578 non-null   int64 
1   purpose            9578 non-null   object
2   int.rate           9578 non-null   float64
3   installment        9578 non-null   float64
4   log.annual.inc     9578 non-null   float64
5   dti                9578 non-null   float64
6   fico               9578 non-null   int64 
7   days.with.cr.line  9578 non-null   float64
8   revol.bal          9578 non-null   int64 
9   revol.util         9578 non-null   float64
10  inq.last.6mths     9578 non-null   int64 
11  delinq.2yrs        9578 non-null   int64 
12  pub.rec            9578 non-null   int64 
13  not.fully.paid     9578 non-null   int64 
dtypes: float64(6), int64(7), object(1)
memory usage: 1.0+ MB

En este ejemplo, desarrollaremos un modelo para predecir cuáles son los clientes que no han pagado íntegramente el préstamo. Exploremos la columna «purpose» y «target» utilizando el gráfico de recuento de Seaborn. 

import seaborn as sns
import matplotlib.pyplot as plt

sns.countplot(data=df,x='purpose',hue='not.fully.paid')
plt.xticks(rotation=45, ha='right');

Nuestro conjunto de datos presenta un desequilibrio que afectará al rendimiento del modelo. Puedes consultar el tutorial «Remuestrear un conjunto de datos desequilibrado» para adquirir experiencia práctica en el manejo de conjuntos de datos desequilibrados.

Procesamiento de datos 

Ahora convertiremos la columna « purpose » de categórica a entera utilizando la función « get_dummies() » de pandas.

pre_df = pd.get_dummies(df,columns=['purpose'],drop_first=True)
pre_df.head()

A continuación, definiremos las variables de característica (X) y objetivo (y), y dividiremos el conjunto de datos en conjuntos de entrenamiento y prueba. 

from sklearn.model_selection import train_test_split

X = pre_df.drop('not.fully.paid', axis=1)
y = pre_df['not.fully.paid']

X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.33, random_state=125
)

Creación de modelos y formación

La creación y el entrenamiento de modelos es bastante sencillo. Entrenaremos un modelo en un conjunto de datos de entrenamiento utilizando hiperparámetros predeterminados. 

from sklearn.naive_bayes import GaussianNB

model = GaussianNB()

model.fit(X_train, y_train);

Evaluación del modelo

Utilizaremos la precisión y la puntuación f1 para determinar el rendimiento del modelo, y parece que el algoritmo gaussiano Naive Bayes ha funcionado bastante bien. 

from sklearn.metrics import (
    accuracy_score,
    confusion_matrix,
    ConfusionMatrixDisplay,
    f1_score,
    classification_report,
)

y_pred = model.predict(X_test)

accuray = accuracy_score(y_pred, y_test)
f1 = f1_score(y_pred, y_test, average="weighted")

print("Accuracy:", accuray)
print("F1 Score:", f1)

Accuracy: 0.8206263840556786
F1 Score: 0.8686606980013266

Debido a la naturaleza desequilibrada de los datos, podemos ver que la matriz de confusión cuenta una historia diferente. En un objetivo minoritario: not fully paid, tenemos más etiquetas erróneas. 

labels = ["Fully Paid", "Not fully Paid"]
cm = confusion_matrix(y_test, y_pred)
disp = ConfusionMatrixDisplay(confusion_matrix=cm, display_labels=labels)
disp.plot();

Si tienes problemas durante el entrenamiento o la evaluación del modelo, puedes consultar el tutorial sobre clasificación Naive Bayes utilizando el cuaderno de trabajo Scikit-learn DataLab. Incluye un conjunto de datos, código fuente y resultados. 

Problema de probabilidad cero

Supongamos que no hay ninguna tupla para un préstamo de riesgo en el conjunto de datos; en este caso, la probabilidad a posteriori será cero y el modelo no podrá realizar una predicción. Este problema se conoce como probabilidad cero porque la ocurrencia de esa clase en particular es cero.

La solución para este problema es la corrección laplaciana o la transformación de Laplace. La corrección laplaciana es una de las técnicas de suavizado. Aquí, puedes suponer que el conjunto de datos es lo suficientemente grande como para que añadir una fila de cada clase no suponga ninguna diferencia en la probabilidad estimada. Esto resolverá el problema de los valores de probabilidad iguales a cero.

Por ejemplo: Supongamos que para la clase préstamo arriesgado, hay 1000 tuplas de entrenamiento en la base de datos. En esta base de datos, la columna de ingresos tiene 0 tuplas para ingresos bajos, 990 tuplas para ingresos medios y 10 tuplas para ingresos altos. Las probabilidades de que se produzcan estos eventos, sin la corrección laplaciana, son 0, 0,990 (de 990/1000) y 0,010 (de 10/1000).

Ahora, aplica la corrección laplaciana al conjunto de datos proporcionado. Añadamos una tupla más por cada par de valores de ingresos. Las probabilidades de que ocurran estos eventos:

Ventajas de Naive Bayes

• No solo es un enfoque sencillo, sino también un método rápido y preciso para realizar predicciones.
• Naive Bayes tiene un coste computacional muy bajo.
• Puede trabajar de manera eficiente con conjuntos de datos de gran tamaño.
• Funciona bien en el caso de variables de respuesta discretas en comparación con las variables continuas.
• Se puede utilizar con múltiples problemas de predicción de clases.
• También funciona bien en el caso de problemas de análisis de texto.
• Cuando se cumple la hipótesis de independencia, un clasificador Naive Bayes funciona mejor en comparación con otros modelos, como la regresión logística.

Desventajas del método Naive Bayes

• La suposición de características independientes. En la práctica, es casi imposible que el modelo obtenga un conjunto de predictores que sean totalmente independientes.
• Si no hay ninguna tupla de entrenamiento de una clase concreta, esto provoca una probabilidad a posteriori igual a cero. En este caso, el modelo no puede realizar predicciones. Este problema se conoce como problema de probabilidad/frecuencia cero.

Conclusión

¡Enhorabuena, has llegado al final de este tutorial!

En este tutorial, has aprendido sobre el algoritmo Naive Bayes, su funcionamiento, sus supuestos, sus problemas, su implementación, sus ventajas y sus desventajas. A lo largo del camino, también has aprendido a crear y evaluar modelos en scikit-learn para clases binarias y multinomiales.

Naive Bayes es el algoritmo más sencillo y potente. A pesar de los importantes avances en el machine learning en los últimos años, ha demostrado su valía. Se ha implementado con éxito en numerosas aplicaciones, desde el análisis de texto hasta los motores de recomendación.

Si deseas obtener más información sobre scikit-learn en Python, realiza nuestro curso «Aprendizaje supervisado con scikit-learn» y echa un vistazo a nuestro tutorial « » sobre Scikit-Learn: Análisis del béisbol, parte 1.