Cours
L'optimisation est un outil fondamental utilisé dans diverses industries et disciplines pour prendre les meilleures décisions possibles en fonction de contraintes données. Qu'il s'agisse de minimiser les coûts dans une chaîne d'approvisionnement, de maximiser l'efficacité des systèmes énergétiques ou de trouver les paramètres optimaux dans les modèles d'apprentissage automatique, les techniques d'optimisation sont essentielles.
Python, connu pour sa simplicité et sa polyvalence, offre de puissantes bibliothèques pour les problèmes d'optimisation. Parmi ceux-ci, Pyomo se distingue comme une bibliothèque complète et flexible qui permet aux utilisateurs de définir et de résoudre des modèles d'optimisation complexes de manière transparente.
Dans ce tutoriel, nous allons explorer Pyomo depuis le début. Nous couvrirons tout, de l'installation et de la configuration des solveurs à la formulation et à la résolution de différents problèmes d'optimisation !
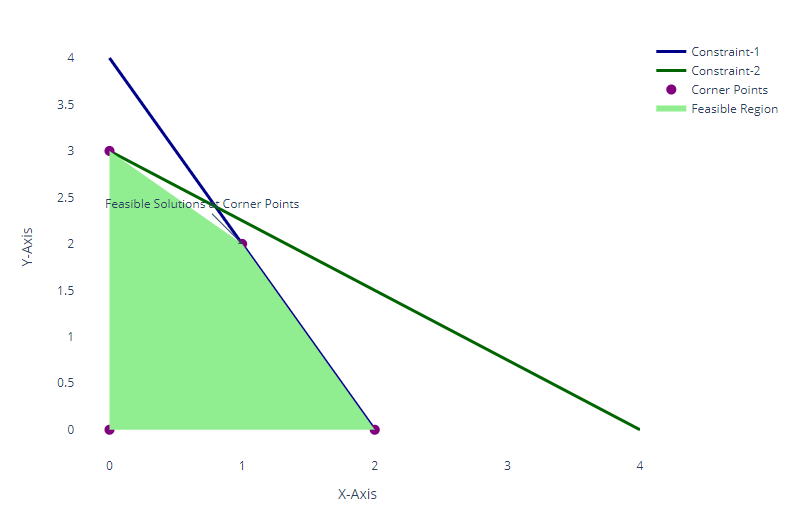
Exploration des solutions faisables dans la programmation linéaire. Image par l'auteur.
Qu'est-ce que Pyomo ?
Pyomo est une bibliothèque open-source permettant de construire et de résoudre des modèles d'optimisation à l'aide de Python. Il vous permet de définir des modèles d'optimisation d'une manière à la fois mathématiquement rigoureuse et syntaxiquement intuitive pour les programmeurs Python. Il prend en charge un large éventail de types de problèmes, notamment :
- Programmation linéaire (LP): LP implique l'optimisation d'une fonction objective linéaire soumise à des contraintes d'égalité et d'inégalité linéaires. Il est largement utilisé pour l'allocation des ressources, l'ordonnancement et les problèmes de planification financière.
- Programmation non linéaire (PNL): NLP traite de l'optimisation d'une fonction objective non linéaire avec des contraintes non linéaires. Il est souvent utilisé en ingénierie et en économie pour des systèmes plus complexes où les relations ne sont pas linéaires.
- Programmation en nombres entiers mixtes (MIP): MIP implique des problèmes d'optimisation où certaines variables sont restreintes à des nombres entiers tandis que d'autres peuvent être continues. Ceci est utile dans des scénarios tels que la conception de la chaîne d'approvisionnement ou la planification de projets, où les décisions peuvent être discrètes (par exemple, marche/arrêt).
- Programmation stochastique: La programmation stochastique aborde les problèmes d'optimisation où certains éléments sont incertains et modélisés comme des variables aléatoires. Elle est couramment appliquée dans les domaines de la finance et de la gestion de la chaîne d'approvisionnement afin d'optimiser les décisions en cas d'incertitude.
- Optimisation dynamique: L'optimisation dynamique fe concentre sur l'optimisation des variables de décision dans le temps, impliquant généralement des systèmes évoluant de manière dynamique. Il est utilisé dans des domaines tels que le contrôle des processus, la robotique et l'économie pour gérer les processus dépendant du temps.
Caractéristiques de Pyomo
Maintenant que nous comprenons mieux Pyomo, passons en revue quelques-unes de ses fonctionnalités les plus importantes.
Flexibilité et extensibilité
La flexibilité de Python vient de sa capacité à modéliser des relations complexes à l'aide de constructions Python standard. Il s'intègre à divers solveurs commerciaux et open-source, ce qui facilite la résolution de nombreux problèmes d'optimisation.
Syntaxe Python
Les modèles Pyomo sont construits sur Python et écrits en utilisant la syntaxe standard de Python. La courbe d'apprentissage est donc douce pour ceux qui connaissent Python et vous permet d'utiliser les vastes bibliothèques de Python dans vos modèles.
Une communauté et une documentation solides
Pyomo dispose d'une solide communauté d'utilisateurs et d'une documentation complète, qui comprend des exemples et des tutoriels pour aider les utilisateurs à tous les niveaux.
Cas d'utilisation de Pyomo
Pyomo a un large éventail d'applications dans le monde réel. En voici quelques-unes :
1. Optimisation de la chaîne d'approvisionnement
L'optimisation de la chaîne d'approvisionnement consiste à améliorer la logistique, à gérer les niveaux de stocks et à créer des calendriers de production efficaces.
Il peut s'agir de minimiser les coûts de transport, d'optimiser l'emplacement des entrepôts ou d'équilibrer l'offre et la demande.
Par exemple, une entreprise peut avoir besoin de répondre à la demande de ses clients dans plusieurs régions tout en minimisant les coûts d'expédition et en maintenant les niveaux de stock dans chaque centre de distribution.
2. Modélisation financière
Dans la modélisation financière, l'optimisation permet d'allouer des ressources, telles que le capital, afin de maximiser les rendements tout en minimisant les risques.
Il peut s'agir d'une optimisation de portefeuille, où les investisseurs équilibrent le risque et le rendement en sélectionnant une combinaison d'actifs sous réserve de contraintes telles que les limites budgétaires, les exigences réglementaires ou la tolérance au risque.
La modélisation financière permet de s'assurer que les stratégies financières s'alignent sur les objectifs à long terme tout en atténuant les risques potentiels.
3. Systèmes énergétiques
L'optimisation des systèmes énergétiques vise à maximiser l'efficacité de la production, de la distribution et de la consommation d'énergie.
Il peut s'agir de déterminer la combinaison optimale de sources d'énergie (par exemple, renouvelables ou non) tout en minimisant les coûts des combustibles, en respectant les limites d'émission et en s'adaptant à la fluctuation de la demande.
Ce type d'optimisation joue un rôle central dans la gestion du réseau, l'exploitation des centrales électriques et la réduction des impacts environnementaux.
4. Apprentissage automatique et science des données
L'optimisation est au cœur de nombreuses tâches d'apprentissage automatique et de science des données, telles que l'ajustement des hyperparamètres et la sélection des caractéristiques.
Dans l'ajustement des hyperparamètres, les algorithmes d'optimisation aident à trouver la meilleure configuration de modèle pour améliorer la performance prédictive.
La sélection des caractéristiques, autre tâche essentielle, consiste à identifier les caractéristiques les plus importantes qui contribuent à la précision d'un modèle, ce qui permet de réduire la complexité et d'améliorer l'efficacité.
Maintenant que le contexte est posé, passons à la pratique et commençons à appliquer Pyomo à quelques exemples de problèmes de modélisation !
Apprenez Python à partir de zéro
Configuration de Pyomo
Avant de nous plonger dans la modélisation, nous devons configurer notre environnement en installant Pyomo et en choisissant un solveur approprié.
1. Conditions préalables
Pour utiliser pyomo, vous devez disposer de Python 3.6 ou plus. Pyomo peut être installé via pip.
pip install pyomoCe tutoriel a été créé avec la version de pyomo 6.8.0.
import pyomo
print(pyomo.__version__)Sortie :
>>> 6.8.02. Choisir et installer le bon solveur
Dans le domaine de l'optimisation, les solveurs sont essentiels, car ce sont les algorithmes qui trouvent la solution optimale au problème que vous avez défini. Différents solveurs sont mieux adaptés en fonction du type de problème (par exemple, linéaire, non linéaire, entier). Pyomo est un outil de modélisation qui s'appuie sur des solveurs externes pour effectuer les calculs.
Passons en revue quelques-unes des solutions les plus courantes.
Solveurs libres
1. GLPK (Kit de programmation linéaire GNU)
GLPK est un outil populaire pour la résolution de problèmes de programmation linéaire (LP) et de programmation mixte en nombres entiers (MIP).
Il s'agit d'un excellent choix pour les tâches d'optimisation linéaire de base et il est largement utilisé dans les applications universitaires et industrielles.
Installation
- Fenêtres : Téléchargez et installez GLPK.
- macOS :
brew install glpk- Linux :
sudo apt-get install glpk-utils2. CBC (Coin-or Branch and Cut)
CBC est un solveur open-source pour les problèmes de programmation linéaire (LP) et de programmation mixte en nombres entiers (MIP).
Il offre des fonctionnalités avancées et de meilleures performances, dans certains cas, par rapport à GLPK, ce qui en fait une option solide pour les tâches d'optimisation plus complexes.
CBC peut être installé via le gestionnaire de paquets conda.
conda install -c conda-forge coincbc3. IPOPT (Interior Point OPTimizer)
IPOPT est un puissant solveur conçu pour les problèmes de problèmes de programmation non linéaire (NLP) à grande échelle.
Il est particulièrement bien adapté à la gestion de modèles complexes et non linéaires, ce qui en fait un excellent choix pour les problèmes dépassant l'optimisation linéaire.
IPOPT peut être installé via le gestionnaire de paquets conda.
!conda install -c conda-forge ipoptRésolveurs commerciaux
1. CPLEX
CPLEX est un solveur d'optimisation de pointe qui traite efficacement les problèmes de programmation linéaire (LP), de programmation mixte en nombres entiers (MIP) et de programmation quadratique (QP).
Il nécessite une licence d'IBM mais est disponible gratuitement pour les utilisateurs universitaires, ce qui en fait un excellent choix pour la recherche et l'enseignement.
2. Gurobi
Gurobi est un solveur commercial de premier plan, connu pour sa rapidité et son efficacité dans la résolution des problèmes de programmation non linéaire (NLP), LP, MIP et QP.
Comme CPLEX, il nécessite une licence mais offre un accès gratuit aux utilisateurs universitaires. Il s'agit donc d'un outil standard de l'industrie pour l'optimisation avancée.
Logiciels libres et logiciels commerciaux
Les solveurs open-source tels que GLPK et CBC sont gratuits et suffisent pour la plupart des besoins d'optimisation de base. Ce sont d'excellents choix pour les projets à petite échelle et à des fins éducatives.
Toutefois, les solveurs commerciaux tels que CPLEX et Gurobi offrent généralement des performances supérieures, en particulier pour les problèmes plus importants et plus complexes. Ces solveurs présentent des caractéristiques avancées, notamment une meilleure prise en charge de la programmation quadratique et non linéaire, et sont optimisés pour des applications industrielles à grande échelle.
Alors que les solveurs open-source peuvent gérer de nombreuses tâches d'optimisation de routine, les solveurs commerciaux sont souvent un meilleur choix lorsqu'il s'agit de répondre à des besoins plus complexes et plus performants.
Gardez à l'esprit que les solveurs commerciaux nécessitent une licence, bien qu'ils soient disponibles gratuitement pour les utilisateurs universitaires.
Voyons maintenant comment configurer un solveur dans Pyomo. J'utiliserai GLPK dans ce cas.
3. Configurer un solveur dans Pyomo
Tout d'abord, assurez-vous que l'exécutable du solveur se trouve dans le PATH de votre système après l'installation.
Ensuite, créez un script Python et ajoutez ce qui suit :
from pyomo.environ import SolverFactory
solver = SolverFactory('glpk')Pour confirmer que Pyomo et votre solveur sont correctement installés, résolvons un simple problème de test.
Problème de test : programme linéaire simple
Objectif: Minimiser Z=x+y
Objet:
- x + 2y ≥ 4
- x - y ≤ 1
- x ≥ 0
- y ≥ 0
Ce problème consiste à trouver la plus petite valeur possible de Z, qui est la somme de deux variables, x et y. Cependant, x et y doivent remplir certaines conditions .
Tout d'abord, lorsque vous additionnez x et deux fois y, le résultat doit être au moins égal à 4. Deuxièmement, x moins y doit être inférieur ou égal à 1. Enfin, les deux x et y doivent être nuls ou positifs (ils ne peuvent pas être négatifs).
L'objectif est de trouver les valeurs de x et de y qui satisfont à ces conditions tout en rendant Z aussi petit que possible.
Mise en œuvre à l'aide de Pyomo :
import pyomo.environ as pyo
# Create a model
model = pyo.ConcreteModel()
# Define variables
model.x = pyo.Var(within=pyo.NonNegativeReals)
model.y = pyo.Var(within=pyo.NonNegativeReals)
# Define objective
model.obj = pyo.Objective(expr=model.x + model.y, sense=pyo.minimize)
# Define constraints
model.con1 = pyo.Constraint(expr=model.x + 2 * model.y >= 4)
model.con2 = pyo.Constraint(expr=model.x - model.y <= 1)
# Select solver
solver = pyo.SolverFactory('glpk')
# Solve the problem
result = solver.solve(model)
# Display results
print('Status:', result.solver.status)
print('Termination Condition:', result.solver.termination_condition)
print('Optimal x:', pyo.value(model.x))
print('Optimal y:', pyo.value(model.y))
print('Optimal Objective:', pyo.value(model.obj))Si tout fonctionne correctement, le résultat attendu est le suivant :
Status: ok
Termination Condition: optimal
Optimal x: 0.0
Optimal y: 2.0
Optimal Objective: 2.0Examinons le code ci-dessus : Tout d'abord, il définit deux variables, x et y, qui ne peuvent prendre que des valeurs non négatives. L'objectif du modèle est de minimiser la somme des x et y (x + y). Le code définit le solveur comme glpk pour trouver les valeurs optimales de x et y qui satisfont ces contraintes tout en minimisant l'objectif.
Après avoir exécuté le code, nous constatons que les valeurs optimales des variables sont x = 0,0 et y = 2,0, ce qui minimise la fonction objective Z = x + y. Par conséquent, la valeur minimale de la fonction objective est 2.0, ce qui satisfait les contraintes données.
Les bases de la modélisation avec Pyomo
Comprendre comment définir les composants de base d'un modèle d'optimisation dans Pyomo est nécessaire pour mettre en place et résoudre des problèmes d'optimisation de manière efficace.
1. Définition des variables
Les variables représentent les décisions à prendre dans un problème d'optimisation. Dans Pyomo, les variables sont les quantités que le solveur ajustera pour optimiser la fonction objective tout en satisfaisant toutes les contraintes.
Variables scalaires
Une variable scalaire est une variable unique qui n'est pas indexée sur un ensemble. Pour définir une variable scalaire dans Pyomo, vous utilisez la classe Var du module pyomo.environ.
from pyomo.environ import Var
model.x = Var()Nous commençons par importer le fichier Var et créons une variable x à l'aide de Var(). Cette variable n'a pas de limites spécifiées, ce qui signifie qu'elle peut prendre n'importe quelle valeur réelle, sauf contrainte contraire dans le modèle.
Ajout de bornes
Vous pouvez restreindre les valeurs qu'une variable peut prendre en spécifiant des limites. Les limites sont définies comme un tuple (lower_bound, upper_bound) :
from pyomo.environ import Var
model.x = Var(bounds=(0, None))Spécifier les domaines
Pyomo fournit des domaines prédéfinis que vous pouvez utiliser pour spécifier le type de valeurs qu'une variable peut prendre, comme NonNegativeReals, Integers, ou Binary:
from pyomo.environ import Var, NonNegativeReals
model.x = Var(domain=NonNegativeReals)Variables indexées
Lorsque vous avez affaire à plusieurs variables de nature similaire, telles que des variables représentant des périodes ou des éléments différents, il est efficace d'utiliser des variables indexées. Les variables indexées sont des variables définies sur un ensemble.
import pyomo.environ as pyo
model.I = pyo.Set(initialize=[1, 2, 3])
model.y = pyo.Var(model.I, domain=pyo.NonNegativeReals)Supposons que vous modélisiez les quantités produites pour trois produits. Vous pouvez définir :
model.Products = pyo.Set(initialize=['A', 'B', 'C'])
model.production = pyo.Var(model.Products, domain=pyo.NonNegativeReals)Maintenant, model.production['A'], model.production['B'], et model.production['C'] représentent les quantités produites pour les produits A, B, et C, respectivement.
2. Définir les objectifs
La fonction objective est ce que nous essayons d'optimiser (minimiser ou maximiser). Elle définit l'objectif du modèle, comme la minimisation des coûts ou la maximisation des bénéfices, et est généralement exprimée sous la forme d'une équation mathématique impliquant les variables de décision.
Ils sont définis à l'aide de la classe Objective:
from pyomo.environ import ConcreteModel, Var, Objective, minimize, maximize, NonNegativeReals
# Create a model
model = ConcreteModel()
# Define variables
model.x = Var(within=NonNegativeReals)
model.y = Var(within=NonNegativeReals)
# Minimization (cost)
model.cost = Objective(expr=2 * model.x + 3 * model.y, sense=minimize)
# When Maximization profit - (can have one objective at a time)
# model.profit = Objective(expr=5 * model.x + 4 * model.y, sense=maximize)3. Ajouter des contraintes
Les contraintes définissent les limites ou les exigences du problème :
from pyomo.environ import Constraint
model.con1 = Constraint(expr=model.x + model.y >= 10)L'exemple ci-dessus définit une contrainte dans le modèle Pyomo à l'aide de la classe Constraint. La contrainte model.con1 précise que la somme des variables x et y doit être supérieure ou égale à 10.
4. Paramétrage des modèles
Les paramètres sont des valeurs fixes utilisées dans le modèle pour représenter des quantités connues ou des constantes qui ne changent pas au cours du processus d'optimisation.
Ils aident à définir les relations entre les variables et les contraintes, en structurant le modèle par l'intégration de données ou d'hypothèses du monde réel :
from pyomo.environ import Param
model.p = Param(initialize=5)Le code ci-dessus définit un paramètre p dans le modèle Pyomo en utilisant la classe Param et l'initialise avec une valeur fixe de 5. Le paramètre p peut maintenant être utilisé dans le modèle pour représenter une valeur constante qui ne change pas pendant le processus d'optimisation.
Travaillons maintenant sur un problème d'optimisation de bout en bout !
Exemple Pyomo de bout en bout
Voyons un exemple de bout en bout de la résolution d'un problème d'optimisation à l'aide de Pyomo. Nous modéliserons un scénario réel dans lequel une usine fabrique deux produits et dont l'objectif est de maximiser le profit tout en tenant compte des contraintes de temps des machines.
1. Énoncé du problème
Une usine fabrique deux produits, P1 et P2. Le bénéfice par unité est de :
- P1: $40
- P2: $50
Temps machine disponible :
- Machine A: 100 heures
- Machine B: 80 heures
- Machine C: 90 heures
Temps nécessaire par unité :
|
Produit |
Machine A (heures) |
Machine B (heures) |
Machine C (heures) |
|
P1 |
1 |
2 |
0 |
|
P2 |
2 |
1 |
3 |
Objectif : Maximiser les bénéfices.
Variables de décision:
- x₁ : Unités de P1 à produire.
- x₂ : Unités de P2 à produire.
2. Formulation mathématique
Fonction objective:
Maximiser Z = 40x₁ + 50x₂
Contraintes:
- Capacité de la machine A: 1x₁ + 2x₂ ≤ 100
- Capacité de la machine B : 2x₁ + 1x₂ ≤ 80
- Capacité de la machine C : 3x₂ ≤ 90
- Non-négativité : x₁, x₂ ≥ 0
3. Mise en œuvre
Sur la base de l'objectif et des contraintes du problème, voici le code Python pour le modéliser, toujours à l'aide de GLPK.
# Step 1: Import Libraries
import pyomo.environ as pyo
# Step 2: Create a Concrete Model
model = pyo.ConcreteModel()
# Step 3: Define Decision Variables (Units of P1 and P2 to produce)
model.x1 = pyo.Var(within=pyo.NonNegativeReals)
model.x2 = pyo.Var(within=pyo.NonNegativeReals)
# Step 4: Define the Objective Function (Maximize profit)
model.profit = pyo.Objective(expr=40 * model.x1 + 50 * model.x2, sense=pyo.maximize)
# Step 5: Define Constraints
# Machine A capacity constraint: 1x1 + 2x2 <= 100
model.machine_a = pyo.Constraint(expr=1 * model.x1 + 2 * model.x2 <= 100)
# Machine B capacity constraint: 2x1 + 1x2 <= 80
model.machine_b = pyo.Constraint(expr=2 * model.x1 + 1 * model.x2 <= 80)
# Machine C capacity constraint: 3x2 <= 90
model.machine_c = pyo.Constraint(expr=3 * model.x2 <= 90)
# Step 6: Solve the Model using GLPK solver
solver = pyo.SolverFactory('glpk')
result = solver.solve(model)
# Step 7: Analyze Results
# Display Solver Status and Termination Condition
print('Solver Status:', result.solver.status)
print('Termination Condition:', result.solver.termination_condition)
# Get and display the optimal values for x1, x2, and the maximum profit
x1_opt = pyo.value(model.x1)
x2_opt = pyo.value(model.x2)
profit_opt = pyo.value(model.profit)
print(f'Optimal production of P1 (x1): {x1_opt}')
print(f'Optimal production of P2 (x2): {x2_opt}')
print(f'Maximum Profit: ${profit_opt}')Sortie :
>>> Solver Status: ok
>>> Termination Condition: optimal
>>> Optimal production of P1 (x1): 25.0
>>> Optimal production of P2 (x2): 30.0
>>> Maximum Profit: $2500.0Dans le code ci-dessus, nous définissons un modèle d'optimisation linéaire afin de maximiser le bénéfice de la production de deux produits(P1 et P2). La fonction objective est fixée de manière à maximiser le profit, chaque unité de P1 contribuant à hauteur de 40 dollars et chaque unité de P2 contribuant à hauteur de 50 dollars.
Nous imposons trois contraintes représentant les limites de temps des machines A, B et C.
Enfin, nous utilisons le solveur GLPK pour résoudre le problème.
La réponse finale est la suivante produire 25 unités de P1 et 30 unités de P2, ce qui nous permettra de réaliser un bénéfice maximal de 2 500 $..
Fonctionnalités avancées de Pyomo
Dans la section précédente, nous avons vu à quel point il est facile d'implémenter un problème d'optimisation de bout en bout avec Pyomo. Cependant, la plupart des problèmes de la vie réelle ne sont pas simples à résoudre.
Dans cette section, je présente quelques fonctions avancées que vous pouvez utiliser pour résoudre des scénarios plus complexes.
1. Optimisation non linéaire
L'optimisation non linéaire minimise ou maximise une fonction objective non linéaire soumise à des contraintes non linéaires. Examinons un exemple dans lequel nous minimisons la somme des carrés des différences sous réserve d'une contrainte circulaire.
Énoncé du problème
Minimiser l'objectif : Z = (x - 1)² + (y - 2)²
Sous réserve de :
- x² + y² ≤ 4
- x, y ≥ 0
Dans Pyomo, nous pouvons définir les variables de décision x et y avec des limites de 0 pour garantir la non-négativité. La fonction objective s'écrit comme la somme des carrés des différences entre des points spécifiques, et la contrainte garantit que la solution se trouve à l'intérieur d'un cercle de rayon 2.
Dans ce cas, le solveur IPOPT convient pour sa capacité à résoudre des problèmes d'optimisation non linéaire :
import pyomo.environ as pyo
model = pyo.ConcreteModel()
# Define variables with lower bounds
model.x = pyo.Var(bounds=(0, None))
model.y = pyo.Var(bounds=(0, None))
# Objective function: minimize (x - 1)² + (y - 2)²
model.obj = pyo.Objective(expr=(model.x - 1)**2 + (model.y - 2)**2, sense=pyo.minimize)
# Constraint: x² + y² ≤ 4 (circle of radius 2)
model.circle = pyo.Constraint(expr=model.x**2 + model.y**2 <= 4)
solver = pyo.SolverFactory('ipopt')
result = solver.solve(model)
print('Optimal x:', pyo.value(model.x))
print('Optimal y:', pyo.value(model.y))
print('Minimum Z:', pyo.value(model.obj))2. Programmation en nombres entiers mixtes (MIP)
La programmation en nombres entiers mixtes est utilisée lorsque certaines variables de décision sont des nombres entiers (souvent binaires) tandis que d'autres sont continues. Elle est précieuse pour les problèmes de prise de décision tels que la localisation des installations et la planification de la production.
Énoncé du problème
Une entreprise doit décider d'ouvrir des entrepôts sur les sites A, B et C. L'objectif est de minimiser le coût total, qui comprend les coûts fixes d'ouverture des entrepôts et les coûts de transport.
Nous commençons par initialiser les données, y compris les coûts fixes d'ouverture des entrepôts, les coûts de transport, les limites de capacité et la demande totale :
locations = ['A', 'B', 'C']
FixedCost = {'A': 1000, 'B': 1200, 'C': 1500}
TransportCost = {'A': 5, 'B': 4, 'C': 6}
Capacity = {'A': 100, 'B': 80, 'C': 90}
Demand = 150
model = pyo.ConcreteModel()
# Binary variable: 1 if warehouse is open, 0 otherwise
model.y = pyo.Var(locations, domain=pyo.Binary)
# Continuous variable: amount of goods transported
model.x = pyo.Var(locations, domain=pyo.NonNegativeReals)
model.cost = pyo.Objective(
expr=sum(FixedCost[i] * model.y[i] + TransportCost[i] * model.x[i] for i in locations),
sense=pyo.minimize
)
# Demand constraint
model.demand = pyo.Constraint(expr=sum(model.x[i] for i in locations) >= Demand)
# Capacity constraints
def capacity_rule(model, i):
return model.x[i] <= Capacity[i] * model.y[i]
model.capacity = pyo.Constraint(locations, rule=capacity_rule)
solver = pyo.SolverFactory('cbc')
result = solver.solve(model)
for i in locations:
print(f"Warehouse {i}: Open={pyo.value(model.y[i])}, Transported={pyo.value(model.x[i])}")
print('Minimum Total Cost:', pyo.value(model.cost))Le modèle comprend deux types de variables de décision : une variable binaire y qui indique si un entrepôt est ouvert (1 si ouvert, 0 sinon), et une variable continue x qui représente la quantité de marchandises transportées à partir de chaque entrepôt.
La fonction objective additionne les coûts fixes et les coûts de transport de chaque entrepôt et minimise le total. Les contraintes garantissent que le total des marchandises transportées répond à la demande et que la capacité de chaque entrepôt n'est pas dépassée s'il est ouvert.
3. Traiter des objectifs multiples
Parfois, les problèmes d'optimisation impliquent des objectifs multiples qui peuvent entrer en conflit, par exemple maximiser le profit tout en minimisant l'impact sur l'environnement. Une approche courante est laméthode de la somme pondérée , où chaque objectif se voit attribuer un poids pour équilibrer son importance.
Énoncé du problème
Notre objectif est de maximiser les profits tout en minimisant l'impact sur l'environnement :
- Bénéfice : Z₁ = 3x + 5y
- Impact sur l'environnement : Z₂ = 2x + y
Nous pouvons combiner ces objectifs en utilisant les poids w1=0.6, w2=0.4, où l'objectif total devient une somme pondérée :
w1 = 0.6
w2 = 0.4
model.obj = pyo.Objective(
expr=w1 * (3 * model.x + 5 * model.y) - w2 * (2 * model.x + model.y),
sense=pyo.maximize
)Dans cet objectif combiné, nous maximisons le profit tout en minimisant l'impact sur l'environnement en ajustant les poids.
4. Utiliser des sources de données externes
Lorsque vous traitez de grands ensembles de données, il est souvent utile d'importer des données à partir de sources externes telles que des fichiers CSV. Pyomo fonctionne bien avec Pandas pour lire et utiliser des données externes.
Nous pouvons lire un fichier CSV à l'aide de Pandas et utiliser les données pour initialiser les ensembles et les paramètres de notre modèle :
import pandas as pd
data = pd.read_csv('parameters.csv')
# Define set from CSV data
model.I = pyo.Set(initialize=data['index'].unique())
# Define parameter initialized from CSV data
param_dict = data.set_index('index')['value'].to_dict()
model.param = pyo.Param(model.I, initialize=param_dict)Conseils et bonnes pratiques pour l'utilisation de Pyomo
Lorsque vous travaillez avec Pyomo, il est important que vos modèles soient efficaces, bien documentés et faciles à dépanner.
1. Débogage et dépannage
En construisant des modèles d'optimisation dans Pyomo, il est courant de rencontrer des problèmes tels que des solutions infaisables, des échecs du solveur, ou des résultats incorrects. Voici quelques bonnes pratiques en matière de débogage :
- Contrôler les contraintes : Revoyez vos contraintes si votre modèle ne produit pas de solution réalisable. Des contraintes strictes peuvent rendre un problème infaisable. Utilisez la méthode
.display()de Pyomo pour imprimer les valeurs des variables et des contraintes afin de vérifier qu'elles se comportent comme prévu. - Sortie du solveur : Activez les journaux détaillés du solveur en transmettant
tee=Truelorsque vous appelez la méthodesolve(). Cela permet de savoir où le solveur peut rencontrer des difficultés, par exemple en cas de variables non limitées ou d'infaisabilité. - Testez d'abord des modèles simples : Lorsqu'il s'agit de modèles complexes, testez une version simplifiée. Cela permet d'isoler les problèmes potentiels sans les frais généraux d'un modèle entièrement spécifié.
La résolution des problèmes est beaucoup plus facile si vous l'abordez de manière systématique, en analysant les contraintes, la fonction objective et le retour d'information du solveur.
2. Efficacité de la modélisation
Les problèmes d'optimisation peuvent devenir coûteux en termes de calcul lorsque la taille du modèle augmente. Pour garantir une modélisation efficace, tenez compte des conseils suivants :
- Utilisez l'éparpillement : Évitez de passer par des indices inutiles lorsque vous définissez des contraintes ou des objectifs. L'exploitation de la rareté dans votre problème permet de réduire le temps de calcul.
- Variables binaires ou continues : Dans la mesure du possible, réduisez le nombre de variables binaires ou entières. Les variables continues sont plus faciles à manipuler par les résolveurs, ce qui permet d'obtenir des solutions plus rapides.
- Formulation des contraintes : Les contraintes doivent être aussi simples que possible, tant au niveau de la forme mathématique que de la mise en œuvre. Évitez les non-linéarités inutiles et décomposez les contraintes complexes en contraintes plus petites et plus faciles à gérer.
Les modèles efficaces résolvent les problèmes plus rapidement et sont plus faciles à déboguer et à entretenir.
3. Documentation et maintenance
Maintenir des modèles Pyomo bien documentés est une bonne pratique pour une utilisation et une collaboration à long terme. Une bonne documentation facilite également la révision et la mise à jour des modèles au fil du temps :
- Utilisez des commentaires en ligne : Ajoutez toujours des commentaires pour expliquer l'utilité des variables, des contraintes et de la fonction objective. Ceci est particulièrement important dans les modèles d'optimisation où la logique n'est pas toujours évidente.
- Modularisez votre code : Décomposez votre modèle en sections logiques ou même en fonctions distinctes. Cette approche modulaire peut améliorer la lisibilité et faciliter le débogage et la modification de parties spécifiques du modèle.
- Cursus des modifications du modèle : Conservez un historique des versions de votre modèle, surtout s'il évolue. Utilisez des outils de contrôle de version tels que Git pour suivre les modifications et garantir la traçabilité de toute mise à jour ou amélioration.
Une documentation appropriée et un code structuré rendront vos modèles Pyomo plus accessibles aux futurs collaborateurs et plus faciles à adapter ou à modifier en fonction de l'évolution de vos besoins.
Conclusion
Pyomo est un outil puissant et flexible pour construire et résoudre des modèles d'optimisation en Python. Tout au long de ce tutoriel, nous avons exploré la manière dont Pyomo permet aux utilisateurs de modéliser divers problèmes d'optimisation, de la programmation linéaire à la programmation non linéaire et mixte.
Grâce à sa syntaxe conviviale et à son intégration avec des solveurs, Pyomo rend la formulation et la résolution de problèmes d'optimisation du monde réel accessibles aux débutants comme aux utilisateurs avancés.
Si vous souhaitez en savoir plus sur la résolution de problèmes du monde réel avec l'optimisation, consultez le cours gratuit Introduction à l'optimisation en Python sur DataCamp !
Devenez développeur Python
FAQ
À quoi sert Pyomo ?
Pyomo est une bibliothèque Python open-source utilisée pour définir et résoudre des problèmes d'optimisation complexes, notamment la programmation linéaire, non linéaire et mixte.
Comment installer Pyomo et ses solveurs ?
Vous pouvez installer Pyomo en utilisant pip install pyomo. Les solveurs tels que GLPK et CBC peuvent être installés via des gestionnaires de paquets tels que Homebrew, apt-get ou Conda.
Quels types de problèmes d'optimisation Pyomo peut-il résoudre ?
Pyomo prend en charge un large éventail de problèmes d'optimisation, y compris la programmation linéaire (LP), la programmation non linéaire (NLP), la programmation mixte (MIP) et la programmation stochastique.
Puis-je utiliser Pyomo pour des applications réelles telles que l'optimisation de la chaîne d'approvisionnement ?
Oui, Pyomo est largement utilisé pour des applications réelles telles que l'optimisation de la chaîne d'approvisionnement, la modélisation financière, l'optimisation des systèmes énergétiques et les tâches d'apprentissage automatique.
Quelle est la différence entre les solveurs open-source et commerciaux dans Pyomo ?
Les solveurs open-source tels que GLPK et CBC sont gratuits et suffisants pour de nombreux problèmes, tandis que les solveurs commerciaux tels que Gurobi et CPLEX offrent des performances accrues et des fonctionnalités avancées pour des tâches d'optimisation plus complexes et à plus grande échelle.
