Cours
Après avoir collecté des données et passé des heures à les nettoyer, vous pouvez enfin commencer à explorer ! Cette étape, souvent appelée analyse exploratoire des données (AED), est peut-être la plus importante d'un projet de données. Les connaissances acquises grâce à l'AED ont une incidence sur l'ensemble du processus.
Par exemple, l'une des étapes incontournables de l'AED consiste à vérifier la forme des distributions. L'identification correcte de la forme influe sur de nombreuses décisions prises ultérieurement dans le cadre du projet :
- Autres étapes de prétraitement
- Effectuer ou non la détection et éventuellement la suppression des valeurs aberrantes
- Transformation des caractéristiques ou étapes de mise à l'échelle
- Sélection des caractéristiques
- Sélection d'un algorithme
et ainsi de suite. Bien qu'il existe des illustrations, vous avez besoin de mesures plus fiables pour quantifier les différentes caractéristiques des distributions. Deux de ces mesures sont l'asymétrie et l'aplatissement. Vous pouvez les utiliser pour évaluer la ressemblance entre vos distributions et une distribution normale parfaite.
En terminant cet article, vous apprendrez en détail :
- Que sont l'asymétrie et l'aplatissement ?
- Les types d'asymétrie et d'aplatissement
- L'effet de l'asymétrie et de l'aplatissement sur les modèles d'apprentissage automatique
- Calculer l'asymétrie et le kurtosis en Python manuellement et avec des packages tiers.
- Visualisation des distributions pour vérifier les scores d'asymétrie et d'aplatissement (section complète et amusante)
Commençons !
Qu'est-ce que l'asymétrie ?
La distribution normale est omniprésente : mesures du corps humain, poids des objets, scores de QI, résultats de tests, ou même à la salle de sport :

En plus d'être la distribution préférée de la nature, elle est universellement appréciée par presque tous les algorithmes d'apprentissage automatique. Alors que certains veulent améliorer et stabiliser leurs performances, d'autres refusent catégoriquement de travailler avec autre chose qu'une distribution normale (je m'adresse à vous, modèles linéaires).
Ainsi, pour satisfaire le besoin de normalité des algorithmes, nous avons besoin d'un moyen de mesurer le degré de similitude ou de dissemblance de nos propres distributions par rapport à la courbe en forme de cloche parfaite.
Commençons par les queues. Dans une distribution normale parfaite, les queues sont de longueur égale. En revanche, lorsqu'il y a une asymétrie entre les queues, ce qui donne un aspect penché, écrasé d'un côté, on dit qu'il est de travers. Et vous l'avez deviné, nous mesurons l'ampleur de cette asymétrie avec l'asymétrie.
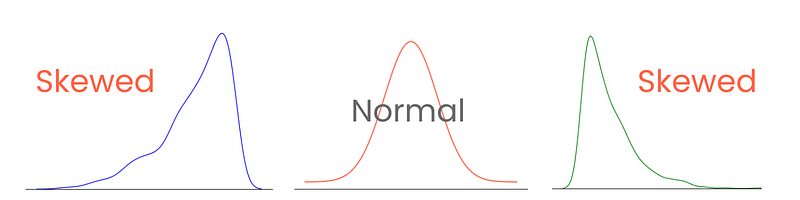
Une catégorisation et une mesure correctes de l'asymétrie permettent de comprendre comment les valeurs se répartissent autour de la moyenne et influencent le choix des techniques statistiques et des transformations de données. Par exemple, les distributions fortement asymétriques peuvent bénéficier de techniques de normalisation ou de mise à l'échelle pour les faire ressembler à une distribution normale. Cela contribuerait à la performance du modèle.
Types d'asymétrie
Il existe trois types d'asymétrie : l'asymétrie positive, l'asymétrie négative et l'asymétrie nulle.
Commençons par le dernier. Une distribution dont l'asymétrie est nulle présente les caractéristiques suivantes :
- Distribution symétrique avec des valeurs uniformément centrées autour de la moyenne.
- Il n'y a pas de biais, d'inclinaison ou de queue d'un côté ou de l'autre.
- La moyenne, la médiane et le mode se trouvent tous au point central.
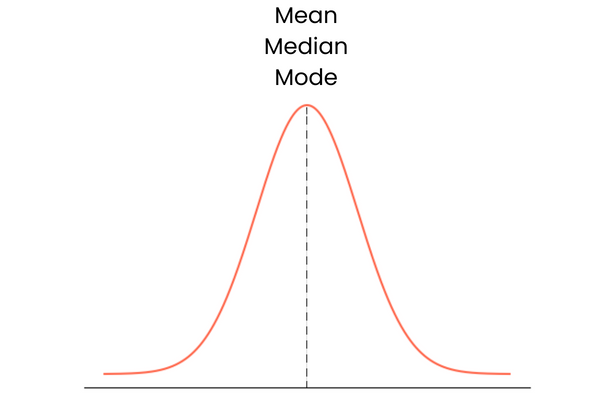
Dans la pratique, la moyenne, la médiane et le mode peuvent ne pas former une ligne droite se chevauchant parfaitement. Elles peuvent être légèrement éloignées l'une de l'autre, mais la différence est trop faible pour avoir de l'importance.
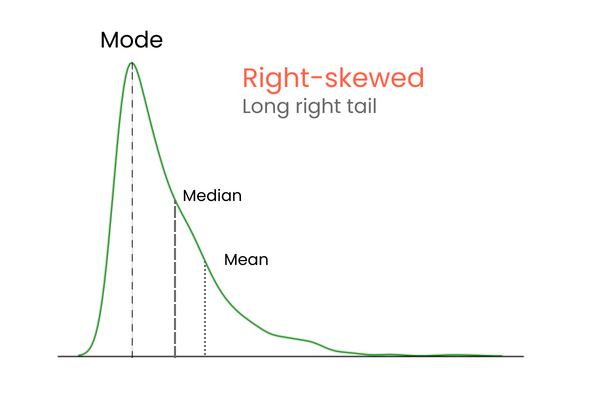
Dans une distribution à asymétrie positive (asymétrie droite) :
- La queue droite de la distribution est plus longue ou plus grosse que la queue gauche.
- La moyenne est supérieure à la médiane et le mode est inférieur à la moyenne et à la médiane.
- Les valeurs inférieures sont regroupées dans la "colline" de la distribution, tandis que les valeurs extrêmes se trouvent dans la longue queue droite.
- Elle est également connue sous le nom de distribution en dents de scie.
Dans une distribution à asymétrie négative (asymétrie gauche) :
- La queue gauche de la distribution est plus longue ou plus grosse que la queue droite.
- La moyenne est inférieure à la médiane et le mode est supérieur à la moyenne et à la médiane.
- Les valeurs les plus élevées sont regroupées dans la "colline" de la distribution, tandis que les valeurs extrêmes se trouvent dans la longue queue gauche.
- Elle est également connue sous le nom de distribution en dents de scie.
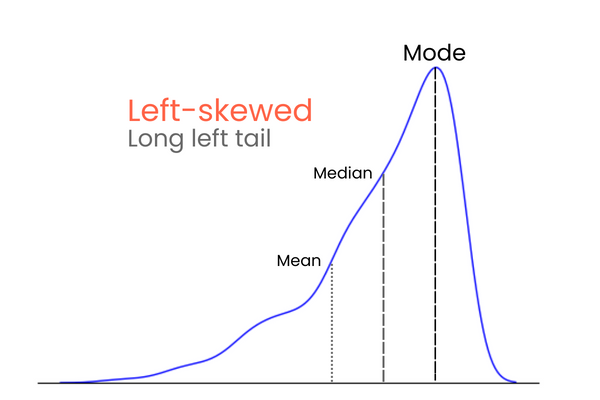
Pour vous rappeler les différences entre l'asymétrie positive et l'asymétrie négative, pensez-y de la manière suivante : si vous voulez augmenter la moyenne d'une distribution, vous devez ajouter des valeurs beaucoup plus élevées que la moyenne à la distribution. Pour abaisser la moyenne, vous devez faire l'inverse, c'est-à-dire introduire dans la distribution des valeurs nettement inférieures à la moyenne. Ainsi, si la majorité des valeurs extrêmes est supérieure à la moyenne, l'asymétrie sera positive car elles augmentent la moyenne. Si la majorité des valeurs extrêmes est inférieure à la moyenne, l'asymétrie est négative car elles diminuent la moyenne.
Comment calculer l'asymétrie (Skewness) en Python
Il existe de nombreuses façons de calculer l'asymétrie, mais la plus simple est le second coefficient d'asymétrie de Pearson, également connu sous le nom d'asymétrie médiane.
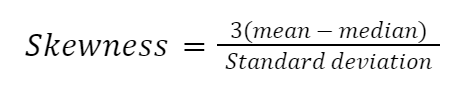
Implémentons la formule manuellement en Python :
import numpy as np
import pandas as pd
import seaborn as sns
# Example dataset
diamonds = sns.load_dataset("diamonds")
diamond_prices = diamonds["price"]
mean_price = diamond_prices.mean()
median_price = diamond_prices.median()
std = diamond_prices.std()
skewness = (3 * (mean_price - median_price)) / std
>>> print(
f"The Pierson's second skewness score of diamond prices distribution is {skewness:.5f}"
)
The Pierson's second skewness score of diamond prices distribution is 1.15189
Une autre formule fortement influencée par les travaux de Karl Pearson est la formule basée sur les moments pour estimer l'asymétrie. Elle est plus fiable et se présente comme suit :
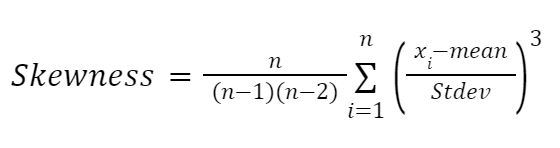
Ici :
- n représente le nombre de valeurs dans une distribution
- x_i denotes each data point
Mettons-le également en œuvre en Python :
def moment_based_skew(distribution):
n = len(distribution)
mean = np.mean(distribution)
std = np.std(distribution)
# Divide the formula into two parts
first_part = n / ((n - 1) * (n - 2))
second_part = np.sum(((distribution - mean) / std) ** 3)
skewness = first_part * second_part
return skewness
>>> moment_based_skew(diamond_prices)
1.618440289857168
Si vous ne voulez pas calculer l'asymétrie manuellement (comme moi), vous pouvez utiliser les méthodes intégrées de pandas ou scipy:
# Pandas version
diamond_prices.skew()
1.618395283383529
# SciPy version
from scipy.stats import skew
skew(diamond_prices)
1.6183502776053016
Bien que toutes les formules d'approximation de l'asymétrie donnent des résultats différents, les différences sont trop faibles pour être significatives ou pour modifier la catégorisation de l'asymétrie. Par exemple, toutes les méthodes que nous avons utilisées aujourd'hui utilisent des formules différentes sous le capot, mais les résultats sont très proches.
Une fois que vous avez calculé l'asymétrie, vous pouvez classer l'ampleur de l'asymétrie par catégorie :
- (-0,5, 0,5) - faible ou approximativement symétrique.
- (-1, -0,5) U (0,5, 1) - modérément asymétrique.
- Au-delà de -1 et 1 - Très asymétrique.
Devenez un scientifique ML
Qu'est-ce que le kurtosis et quels sont ses types ?
Alors que l'asymétrie se concentre sur la dispersion (queues) de la distribution normale, l'aplatissement se concentre davantage sur la hauteur. Elle nous indique à quel point notre distribution normale (ou de type normal) est plate ou en crête. Le terme, qui signifie courbé ou arqué en grec, a été inventé pour la première fois par le mathématicien britannique Karl Pearson (qui a passé sa vie à étudier les distributions de probabilités), ce qui n'est pas surprenant.
Un kurtosis élevé indique :
- Pic aigu au centre de la distribution.
- Plus de valeurs concentrées autour de la moyenne que dans une distribution normale.
- Queues plus lourdes en raison d'une plus grande concentration de valeurs extrêmes ou de valeurs aberrantes dans les queues.
- Probabilité accrue d'événements extrêmes.
D'autre part, un kurtosis faible indique :
- Pic plat.
- Moins de valeurs concentrées autour de la moyenne, mais toujours plus que la distribution normale.
- Queues plus légères.
- Diminution de la probabilité d'événements extrêmes.
Selon leur degré, les distributions présentent trois types d'aplatissement :
- Distribution mésokurtique (kurtosis = 3, excès de kurtosis = 0) : distribution normale parfaite ou très proche.
- Distribution leptokurtique (kurtosis > 3, excès de kurtosis > 0) : pic net, queues lourdes
- Distribution platykurtique (kurtosis < 3, excès de kurtosis < 0) : pic plat, queues légères
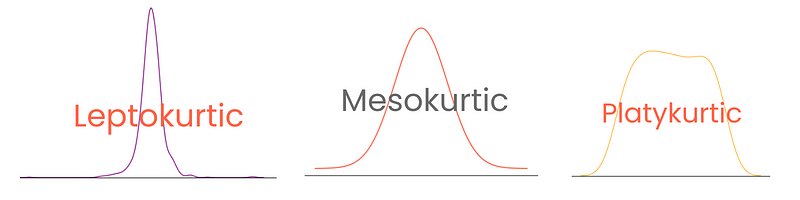
Notez qu'ici, l'excès d'aplatissement est défini comme l'aplatissement - 3, l'aplatissement de la distribution normale étant considéré comme 0. De cette manière, les scores de kurtosis sont plus faciles à interpréter.
Comment calculer le Kurtosis en Python
Vous pouvez calculer l'aplatissement en Python de la même manière que l'asymétrie en utilisant pandas ou SciPy :
from scipy.stats import kurtosis
kurtosis(diamond_prices)
2.177382669056634
Pandas propose deux fonctions pour le kurtosis : kurt et kurtosis. La première est exclusive aux séries Pandas, tandis que vous pouvez utiliser l'autre sur les DataFrame.
diamond_prices.kurt()
2.17769575924869
# Select numeric features and calculate kurtosis
diamonds.select_dtypes(include="number").kurtosis()
carat 1.256635
depth 5.739415
table 2.801857
price 2.177696
x -0.618161
y 91.214557
z 47.086619
dtype: float64
Encore une fois, les chiffres diffèrent pour la distribution car pandas et SciPy utilisent des formules différentes.
Si vous souhaitez calculer manuellement l'aplatissement, vous pouvez utiliser la formule suivante :
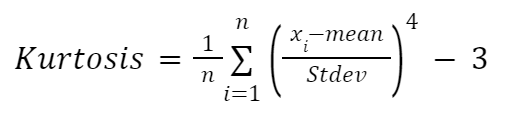
Ici :
- n représente le nombre d'observations dans l'ensemble de données
- x_i désigne chaque point de données individuel
Nous allons à nouveau appliquer la formule à l'intérieur d'une fonction :
def moment_based_kurtosis(distribution):
n = len(distribution)
mean = np.mean(distribution)
std = np.std(distribution)
kurtosis = (1 / n) * sum(((distribution - mean) / std) ** 4) - 3
return kurtosis
>>> moment_based_kurtosis(diamond_prices)
2.1773826690576463
Nous constatons que les prix des diamants ont un excès d'aplatissement de 2,18, ce qui signifie que si nous traçons la distribution, elle aura un pic plus marqué qu'une distribution normale.
C'est donc ce que nous allons faire !
Visualisation du Skewness et du Kurtosis en Python
Le graphique de l'estimation de la densité du noyau (KDE) est l'un des meilleurs moyens de visualiser la forme et, par conséquent, l'asymétrie et l'aplatissement des distributions. Vous pouvez l'utiliser par l'intermédiaire de Seaborn :
import matplotlib.pyplot as plt
sns.kdeplot(diamond_prices)
plt.title("KDE plot of diamond prices")
plt.xlabel("Price ($)")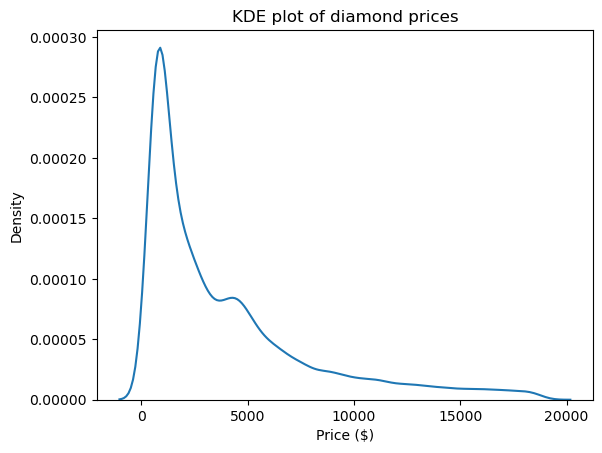
Ce graphique est conforme aux chiffres que nous avons vus jusqu'à présent : la distribution a une longue queue droite, ce qui indique une asymétrie positive, et elle présente un pic très net, ce qui correspond à une aplatissement élevé.
KDE n'est pas la seule parcelle à voir la forme. Nous pouvons également utiliser des histogrammes :
sns.histplot(diamonds["carat"])
plt.xlabel("Carat")
plt.title("A histogram of the carat of diamonds")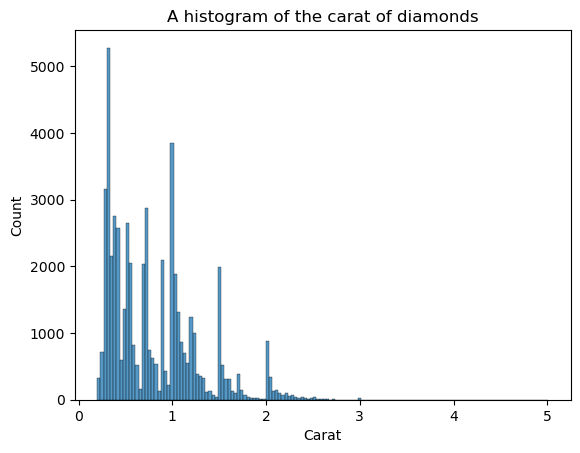
L'inconvénient des histogrammes est que vous devez choisir vous-même le nombre de bins (le nombre de barres). Ici, il y a trop de barres, ce qui crée du bruit dans le visuel - on ne peut pas définir clairement la forme. Diminuons donc le nombre de bacs :
sns.histplot(diamonds["carat"], bins=25)
plt.xlabel("Carat")
plt.title("A histogram of the carat of diamonds")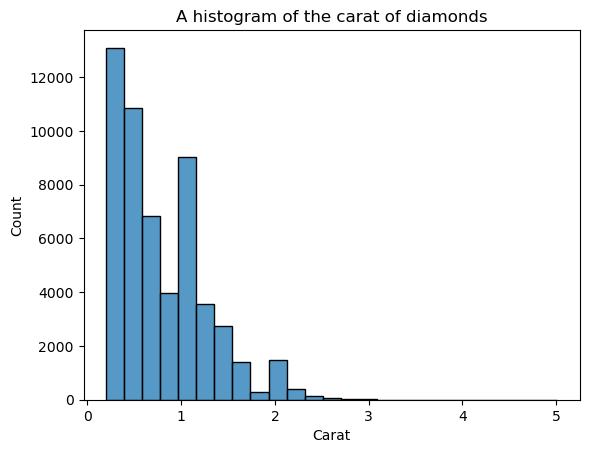
La forme est maintenant mieux définie, mais nous pouvons encore l'améliorer. En plaçant kde=True à l'intérieur de histplot, nous pouvons tracer un KDE de la distribution au-dessus des barres :
sns.histplot(diamonds["carat"], bins=25, kde=True)
plt.xlabel("Carat")
plt.title("A histogram of the carat of diamonds")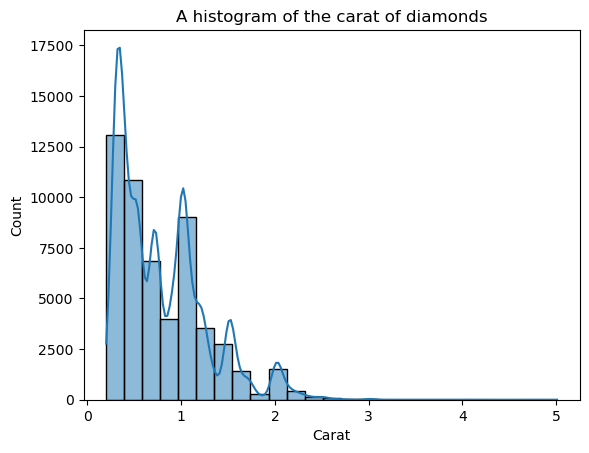
La ligne KDE superposée semble irrégulière, et non la courbe lisse qui nous permet de voir la forme générale. Cette irrégularité s'explique par le fait que la distribution des carats est naturellement irrégulière et éloignée de la distribution normale.
Cependant, nous pouvons réduire la sensibilité de l'EDK à ces fluctuations en ajustant la largeur de bande. Cela se fait à l'aide du paramètre bw_adjust, dont la valeur par défaut est 1 :
# Change the bandwidth from 1 to 3
sns.kdeplot(diamonds["carat"], bw_adjust=3, color="red")
plt.title("KDE of diamond carats");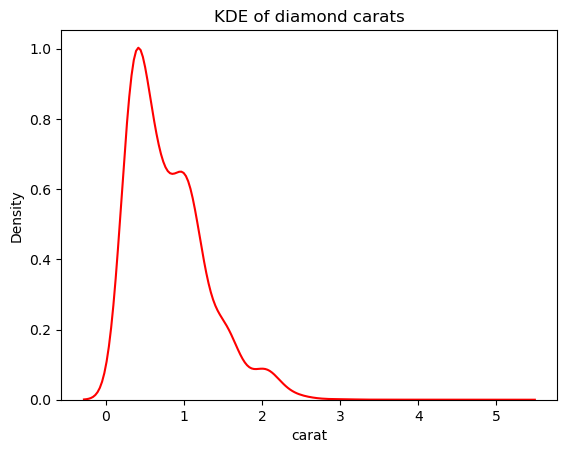
Cette version semble beaucoup moins hérissée que le tracé KDE superposé. Pour ajuster la largeur de bande de l'EDK lors de l'utilisation d'un histogramme superposé à un EDK, vous pouvez utiliser le paramètre kde_kws:
ax = sns.histplot(
diamonds["carat"],
kde=True,
kde_kws=dict(bw_adjust=3),
bins=25,
)
plt.title("An overlaid histogram of diamond carats");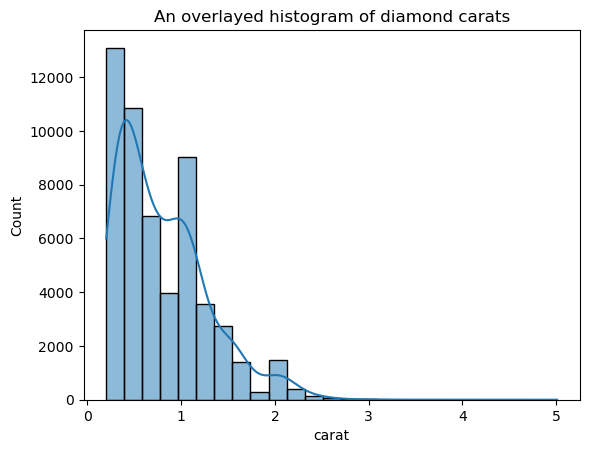
kde_kws accepte tout paramètre acceptable par la fonction kdeplot qui contrôle le calcul de l'EDK.
Une astuce que vous pouvez utiliser lorsque vous tracez des EDK est de supprimer tout ce qui n'est pas la ligne de l'EDK. Étant donné que l'objectif principal d'un EDK est de voir la forme de la distribution, d'autres détails du tracé, tels que les pointes d'axe, les épines et les étiquettes, sont parfois inutiles :
sns.kdeplot(diamond_prices, color="red")
# Remove the spine from three sides
sns.despine(top=True, right=True, left=True)
# Remove the ticks and ticklabels
plt.xticks([])
plt.yticks([])
plt.ylabel("")
plt.xlabel("")
# Set a title
plt.title("Diamond prices", fontdict=dict(fontsize=20));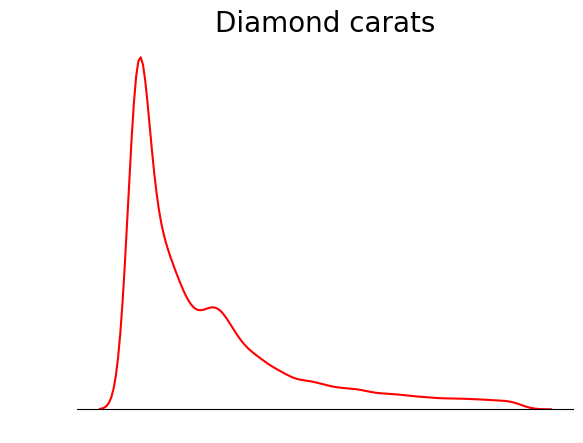
Cette parcelle est beaucoup plus ordonnée. Vous pouvez encore améliorer le graphique en ajoutant des lignes pour indiquer la position de la moyenne, de la médiane et du mode :
sns.kdeplot(diamond_prices, color="red")
sns.despine(top=True, right=True, left=True)
plt.xticks([])
plt.yticks([])
plt.ylabel("")
plt.xlabel("")
plt.title("Diamond prices", fontdict=dict(fontsize=20))
# Find the mean, median, mode
mean_price = diamonds["price"].mean()
median_price = diamonds["price"].median()
mode_price = diamonds["price"].mode().squeeze()
# Add vertical lines at the position of mean, median, mode
plt.axvline(mean_price, label="Mean")
plt.axvline(median_price, color="black", label="Median")
plt.axvline(mode_price, color="green", label="Mode")
plt.legend();
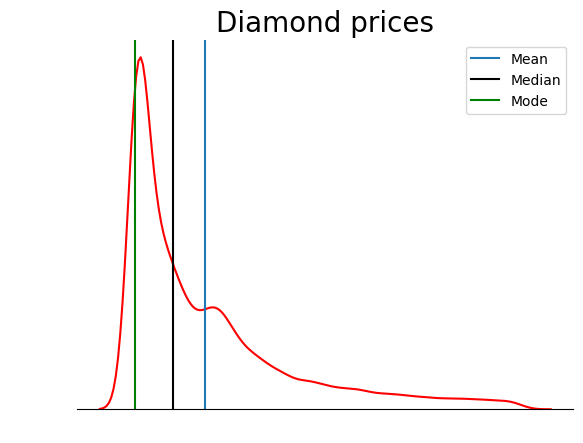
Ce graphique confirme ce que nous avons évoqué dans la section sur les types d'asymétrie : dans une distribution à asymétrie positive, la moyenne est supérieure à la médiane et le mode est inférieur à la moyenne et à la médiane.
Conclusion
L'asymétrie et l'aplatissement, souvent négligés dans l'analyse exploratoire des données, révèlent des informations importantes sur la nature des distributions.
L'asymétrie indique l'inclinaison des données, qu'elles penchent à gauche ou à droite, et révèle leur asymétrie (le cas échéant). Une asymétrie positive signifie que la queue s'étire vers la droite, tandis qu'une asymétrie négative s'oriente dans la direction opposée.
Le kurtosis est une question de pics et de queues. Un kurtosis élevé accentue les pics et alourdit les queues, tandis qu'un kurtosis faible étale les données et allège les queues.
Si vous souhaitez en savoir plus sur l'asymétrie et l'aplatissement, vous pouvez consulter ces excellents cours d'analyse quantitative dispensés par des experts du secteur sur DataCamp :

Je suis un créateur de contenu en science des données avec plus de 2 ans d'expérience et l'un des plus grands followings sur Medium. J'aime écrire des articles détaillés sur l'IA et la ML dans un style un peu sarcastıc, car il faut bien faire quelque chose pour les rendre un peu moins ennuyeux. J'ai produit plus de 130 articles et un cours DataCamp, et un autre est en cours d'élaboration. Mon contenu a été vu par plus de 5 millions de personnes, dont 20 000 sont devenues des adeptes sur Medium et LinkedIn.