Kurs
Nachdem du Daten gesammelt und Stunden damit verbracht hast, sie zu bereinigen, kannst du endlich mit der Erkundung beginnen! Diese Phase, die oft als explorative Datenanalyse (EDA) bezeichnet wird, ist vielleicht der wichtigste Schritt in einem Datenprojekt. Die aus der EDA gewonnenen Erkenntnisse wirken sich auf alle Bereiche aus.
Einer der obligatorischen Schritte in der EDA ist zum Beispiel die Überprüfung der Formen von Verteilungen. Die korrekte Bestimmung der Form beeinflusst viele Entscheidungen im weiteren Verlauf des Projekts, wie z.B:
- Weitere Vorverarbeitungsschritte
- Ob Ausreißer erkannt und eventuell entfernt werden sollen oder nicht
- Schritte zur Umwandlung oder Skalierung von Merkmalen
- Auswahl der Merkmale
- Auswahl des Algorithmus
und so weiter. Es gibt zwar visuelle Darstellungen für diese Aufgabe, aber du brauchst zuverlässigere Kennzahlen, um die verschiedenen Merkmale der Verteilungen zu quantifizieren. Zwei dieser Metriken sind Schiefe und Kurtosis. Du kannst sie verwenden, um die Ähnlichkeit deiner Verteilungen mit einer perfekten Normalverteilung zu beurteilen.
Wenn du diesen Artikel beendest, wirst du im Detail erfahren, wie das geht:
- Was sind Schiefe und Kurtosis?
- Die Arten von Schiefe und Kurtosis
- Der Einfluss von Schiefe und Kurtosis auf Modelle für maschinelles Lernen
- Berechnung von Schiefe und Kurtosis in Python manuell und mit Paketen von Drittanbietern
- Verteilungen visualisieren, um Schiefe und Wölbung zu überprüfen (umfassender und unterhaltsamer Teil)
Lass uns loslegen!
Was ist Schrägheit?
Wir sehen die Normalverteilung überall: bei menschlichen Körpermaßen, Gewichten von Gegenständen, IQ-Werten, Testergebnissen oder sogar im Fitnessstudio:

Sie ist nicht nur die Lieblingsverteilung der Natur, sondern wird auch von fast allen maschinellen Lernalgorithmen geliebt. Manche wollen damit ihre Leistung verbessern und stabilisieren, andere weigern sich regelrecht, mit etwas anderem als einer Normalverteilung zu arbeiten (ich spreche zu dir, lineare Modelle).
Um das Bedürfnis der Algorithmen nach Normalität zu befriedigen, brauchen wir also eine Möglichkeit zu messen, wie ähnlich oder (unähnlich) unsere eigenen Verteilungen der perfekten Glockenkurve sind.
Fangen wir mit den Schwänzen an. Bei einer perfekten Normalverteilung sind die Schwänze gleich lang. Wenn die Schwänze jedoch asymmetrisch sind, so dass sie schief und einseitig aussehen, sprechen wir von einer Schieflage. Und du hast es erraten, wir messen das Ausmaß dieser Asymmetrie mit der Schiefe.
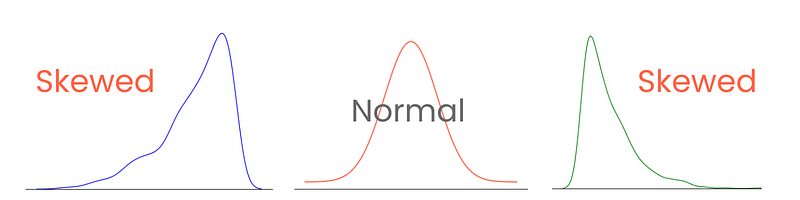
Die korrekte Kategorisierung und Messung der Schiefe gibt Aufschluss darüber, wie die Werte um den Mittelwert herum gestreut sind und beeinflusst die Wahl der statistischen Verfahren und Datentransformationen. Stark schiefe Verteilungen können zum Beispiel von Normalisierungs- oder Skalierungstechniken profitieren, damit sie einer Normalverteilung ähneln. Das würde die Leistung des Modells verbessern.
Arten von Schrägheit
Es gibt drei Arten von Schiefe: positive, negative und Null-Schiefe.
Fangen wir mit der letzten an. Eine Verteilung mit einer Schiefe von Null hat die folgenden Eigenschaften:
- Symmetrische Verteilung mit gleichmäßig um den Mittelwert zentrierten Werten.
- Keine Schräglage, Neigung oder Schwanz zu einer Seite.
- Der Mittelwert, der Median und der Modus liegen alle in der Mitte.
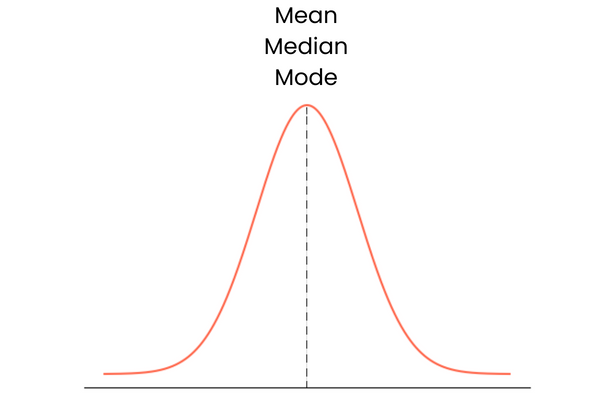
In der Praxis bilden Mittelwert, Median und Modus möglicherweise keine sich perfekt überschneidende gerade Linie. Sie können etwas voneinander entfernt sein, aber der Unterschied wäre zu gering, um eine Rolle zu spielen.
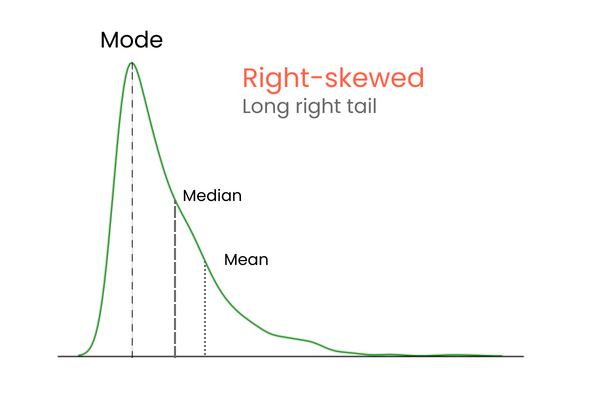
Bei einer Verteilung mit positiver Schiefe (rechtsschief):
- Der rechte Schwanz der Verteilung ist länger oder dicker als der linke.
- Der Mittelwert ist größer als der Median und der Modus ist kleiner als sowohl Mittelwert als auch Median.
- Niedrige Werte befinden sich im "Hügel" der Verteilung, während sich die Extremwerte im langen rechten Schwanz befinden.
- Sie ist auch als rechtsschiefe Verteilung bekannt.
Bei einer Verteilung mit negativer Schiefe (linksschief):
- Der linke Schwanz der Verteilung ist länger oder dicker als der rechte.
- Der Mittelwert ist kleiner als der Median und der Modus ist größer als sowohl Mittelwert als auch Median.
- Höhere Werte befinden sich im "Hügel" der Verteilung, während extreme Werte im langen linken Schwanz zu finden sind.
- Sie ist auch als linksschiefe Verteilung bekannt.
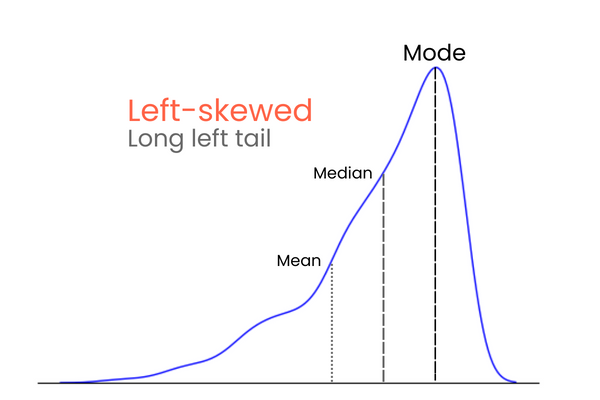
Um dir die Unterschiede zwischen positiver und negativer Schiefe zu merken, stell dir das so vor: Wenn du den Mittelwert einer Verteilung erhöhen willst, solltest du der Verteilung viel höhere Werte als den Mittelwert hinzufügen. Um den Mittelwert zu senken, solltest du das Gegenteil tun und viel niedrigere Werte als den Mittelwert in die Verteilung einführen. Wenn also die Mehrheit der Extremwerte höher ist als der Mittelwert, ist die Schiefe positiv, weil sie den Mittelwert erhöht. Wenn die Mehrheit der Extremwerte kleiner ist als der Mittelwert, ist die Schiefe negativ, weil sie den Mittelwert verringern.
Wie man die Schiefe in Python berechnet
Es gibt viele Möglichkeiten, die Schiefe zu berechnen, aber die einfachste ist der zweite Schiefekoeffizient von Pearson, auch bekannt als Medianschiefe.
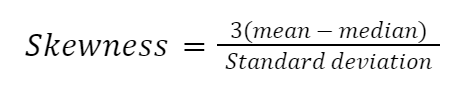
Lass uns die Formel manuell in Python implementieren:
import numpy as np
import pandas as pd
import seaborn as sns
# Example dataset
diamonds = sns.load_dataset("diamonds")
diamond_prices = diamonds["price"]
mean_price = diamond_prices.mean()
median_price = diamond_prices.median()
std = diamond_prices.std()
skewness = (3 * (mean_price - median_price)) / std
>>> print(
f"The Pierson's second skewness score of diamond prices distribution is {skewness:.5f}"
)
The Pierson's second skewness score of diamond prices distribution is 1.15189
Eine weitere Formel, die stark von den Arbeiten von Karl Pearson beeinflusst wurde, ist die momentbasierte Formel zur Annäherung an die Schiefe. Sie ist zuverlässiger und wird wie folgt angegeben:
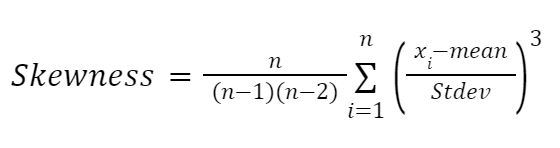
Hier:
- n steht für die Anzahl der Werte in einer Verteilung
- x_i steht für jeden Datenpunkt
Lass uns das auch in Python implementieren:
def moment_based_skew(distribution):
n = len(distribution)
mean = np.mean(distribution)
std = np.std(distribution)
# Divide the formula into two parts
first_part = n / ((n - 1) * (n - 2))
second_part = np.sum(((distribution - mean) / std) ** 3)
skewness = first_part * second_part
return skewness
>>> moment_based_skew(diamond_prices)
1.618440289857168
Wenn du die Schiefe nicht manuell berechnen willst (so wie ich), kannst du die integrierten Methoden von pandas oder scipy verwenden:
# Pandas version
diamond_prices.skew()
1.618395283383529
# SciPy version
from scipy.stats import skew
skew(diamond_prices)
1.6183502776053016
Alle Formeln zur Annäherung an die Schiefe liefern zwar unterschiedliche Werte, aber die Unterschiede sind zu gering, um signifikant zu sein oder die Einstufung der Schiefe zu verändern. Alle Methoden, die wir heute verwendet haben, nutzen unter der Haube unterschiedliche Formeln, aber die Ergebnisse sind sehr ähnlich.
Sobald du die Schiefe berechnest, kannst du das Ausmaß der Schieflage kategorisieren:
- (-0,5, 0,5) - niedrig oder annähernd symmetrisch.
- (-1, -0,5) U (0,5, 1) - mäßig schief.
- Jenseits von -1 und 1 - Stark verzerrt.
Werde ein ML-Wissenschaftler
Was ist Kurtosis und ihre Arten?
Während sich die Schiefe auf die Streuung (Schwänze) der Normalverteilung konzentriert, konzentriert sich die Kurtosis eher auf die Höhe. Sie sagt uns, wie spitz oder flach unsere Normalverteilung (oder normalähnliche Verteilung) ist. Der Begriff stammt aus dem Griechischen und bedeutet "gekrümmt" oder "gewölbt". Er wurde - wenig überraschend - von dem britischen Mathematiker Karl Pearson geprägt (er verbrachte sein Leben mit der Untersuchung von Wahrscheinlichkeitsverteilungen).
Eine hohe Kurtosis zeigt an:
- Scharfe Spitzen in der Mitte der Verteilung.
- Mehr Werte konzentrieren sich um den Mittelwert als bei der Normalverteilung.
- Schwerere Schwänze aufgrund einer höheren Konzentration von Extremwerten oder Ausreißern in den Schwänzen.
- Größere Wahrscheinlichkeit von Extremereignissen.
Andererseits zeigt eine niedrige Kurtosis an:
- Flache Spitze.
- Weniger Werte konzentrieren sich um den Mittelwert, aber immer noch mehr als bei der Normalverteilung.
- Leichtere Schwänze.
- Geringere Wahrscheinlichkeit von Extremereignissen.
Je nach Grad gibt es drei Arten von Kurtosis bei Verteilungen:
- Mesokurtische Verteilung (Kurtosis = 3, Excess Kurtosis = 0): perfekte Normalverteilung oder sehr nahe daran.
- Leptokurtische Verteilung (Kurtosis > 3, Exzess-Kurtosis > 0): scharfe Spitze, starke Schwänze
- Platykurtische Verteilung (Kurtosis < 3, Exzess-Kurtosis < 0): flache Spitze, leichte Schwänze
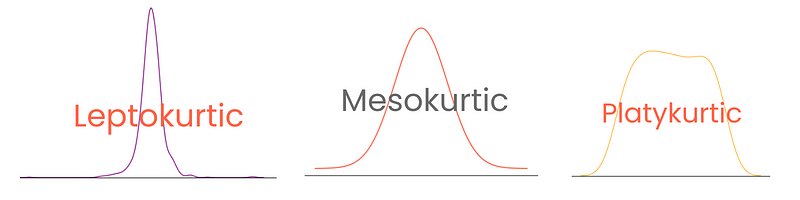
Beachte, dass der Wölbungsüberschuss hier als Wölbung - 3 definiert ist, während die Wölbung der Normalverteilung als 0 behandelt wird. Auf diese Weise sind die Kurtosis-Werte besser interpretierbar.
Wie man die Kurtosis in Python berechnet
Du kannst Kurtosis in Python auf die gleiche Weise wie Skewness mit Pandas oder SciPy berechnen:
from scipy.stats import kurtosis
kurtosis(diamond_prices)
2.177382669056634
Pandas bietet zwei Funktionen für Kurtosis: kurt und kurtosis. Die erste ist exklusiv für Pandas Series, während du die andere für DataFrames verwenden kannst.
diamond_prices.kurt()
2.17769575924869
# Select numeric features and calculate kurtosis
diamonds.select_dtypes(include="number").kurtosis()
carat 1.256635
depth 5.739415
table 2.801857
price 2.177696
x -0.618161
y 91.214557
z 47.086619
dtype: float64
Auch hier unterscheiden sich die Zahlen für die Verteilung, weil Pandas und SciPy unterschiedliche Formeln verwenden.
Wenn du die Kurtosis manuell berechnen möchtest, kannst du die folgende Formel verwenden:
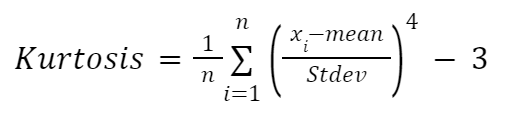
Hier:
- n steht für die Anzahl der Beobachtungen im Datensatz
- x_i steht für jeden einzelnen Datenpunkt
Wir werden die Formel wieder innerhalb einer Funktion implementieren:
def moment_based_kurtosis(distribution):
n = len(distribution)
mean = np.mean(distribution)
std = np.std(distribution)
kurtosis = (1 / n) * sum(((distribution - mean) / std) ** 4) - 3
return kurtosis
>>> moment_based_kurtosis(diamond_prices)
2.1773826690576463
Und wir finden heraus, dass die Diamantenpreise eine übermäßige Kurtosis von 2,18 haben, d.h. wenn wir die Verteilung aufzeichnen, hat sie eine schärfere Spitze als eine Normalverteilung.
Also, lass uns das tun!
Skewness und Kurtosis in Python visualisieren
Eine der besten Darstellungen, um die Form und damit die Schiefe und Kurtosis von Verteilungen zu erkennen, ist eine Kerndichteschätzung (KDE). Es kann über Seaborn genutzt werden:
import matplotlib.pyplot as plt
sns.kdeplot(diamond_prices)
plt.title("KDE plot of diamond prices")
plt.xlabel("Price ($)")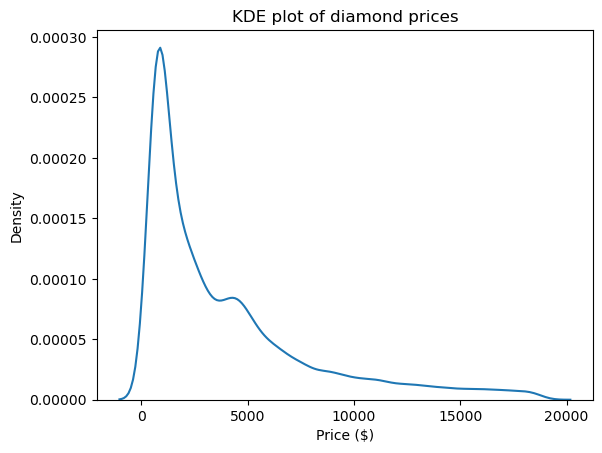
Diese Grafik stimmt mit den Zahlen überein, die wir bisher gesehen haben: Die Verteilung hat einen langen rechten Schwanz, was auf eine positive Schiefe hindeutet, und sie hat eine sehr scharfe Spitze, was einer hohen Kurtosis entspricht.
KDE ist nicht der einzige Plot, bei dem die Form zu sehen ist. Wir können auch Histogramme verwenden:
sns.histplot(diamonds["carat"])
plt.xlabel("Carat")
plt.title("A histogram of the carat of diamonds")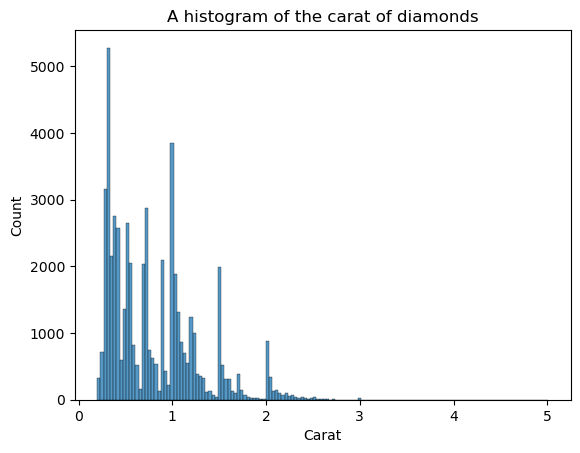
Der Nachteil von Histogrammen ist, dass du die Anzahl der Bins (die Anzahl der Balken) selbst bestimmen musst. Hier gibt es zu viele Balken, die das Bild stören - wir können die Form nicht klar erkennen. Verringern wir also die Anzahl der Bins:
sns.histplot(diamonds["carat"], bins=25)
plt.xlabel("Carat")
plt.title("A histogram of the carat of diamonds")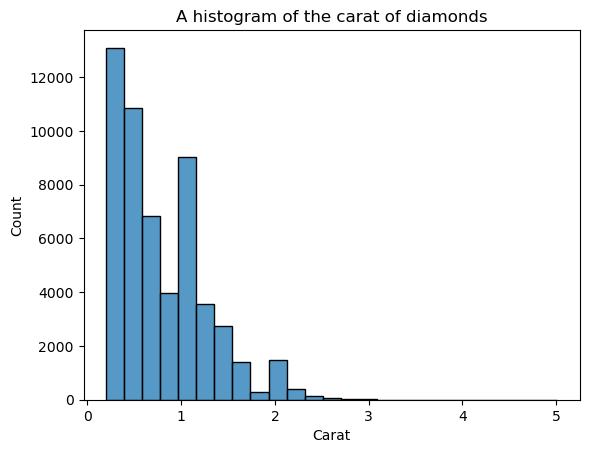
Jetzt ist die Form klarer definiert, aber wir können sie noch weiter verbessern. Wenn du kde=True in histplot einstellst, können wir eine KDE der Verteilung über den Balken zeichnen:
sns.histplot(diamonds["carat"], bins=25, kde=True)
plt.xlabel("Carat")
plt.title("A histogram of the carat of diamonds")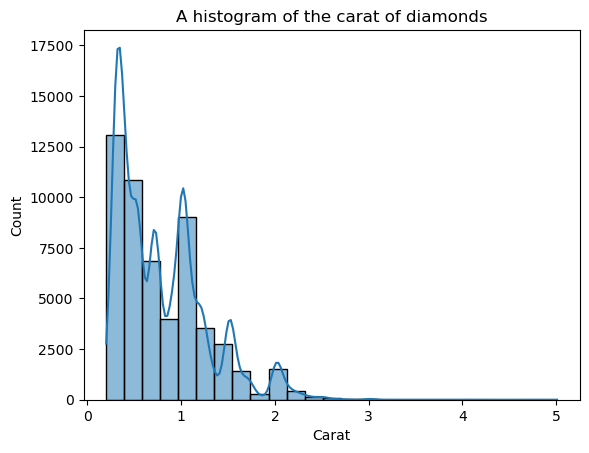
Die überlagerte KDE-Linie sieht zackig aus, nicht wie die glatte Kurve, die uns die allgemeine Form erkennen lässt. Der Grund für die Zerklüftung ist, dass die Karatverteilung von Natur aus spitz zuläuft und weit von der Normalverteilung entfernt ist.
Aber wir können die Empfindlichkeit der KDE gegenüber diesen Schwankungen verringern, indem wir die Bandbreite anpassen. Dies geschieht mit dem Parameter bw_adjust, der standardmäßig auf 1 gesetzt ist:
# Change the bandwidth from 1 to 3
sns.kdeplot(diamonds["carat"], bw_adjust=3, color="red")
plt.title("KDE of diamond carats");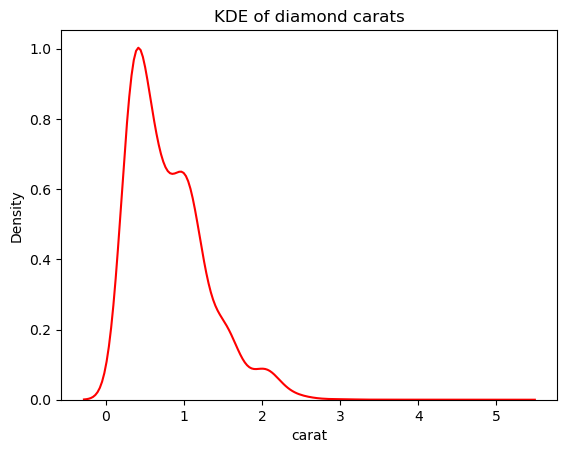
Diese Version sieht viel weniger stachelig aus als die überlagerte KDE-Darstellung. Um die KDE-Bandbreite bei der Verwendung eines Histogramms, das mit einer KDE überlagert ist, anzupassen, kannst du den Parameter kde_kws verwenden:
ax = sns.histplot(
diamonds["carat"],
kde=True,
kde_kws=dict(bw_adjust=3),
bins=25,
)
plt.title("An overlaid histogram of diamond carats");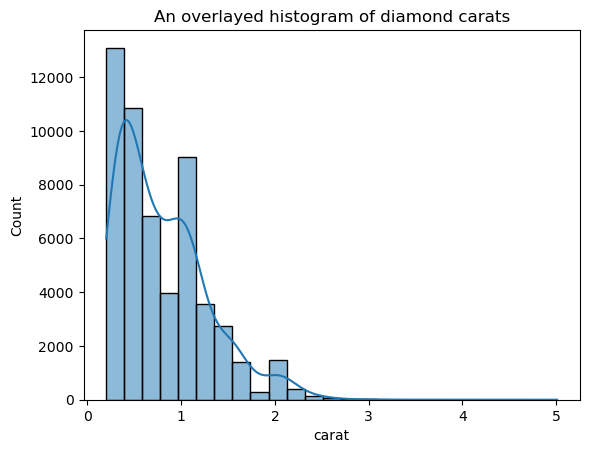
kde_kws akzeptiert jeden Parameter, der von der Funktion kdeplot akzeptiert wird, die die KDE-Berechnung steuert.
Ein Trick, den du beim Plotten von KDEs anwenden kannst, ist, alles außer der KDE-Linie zu entfernen. Da es bei einer KDE in erster Linie darum geht, die Form der Verteilung zu sehen, sind andere Details der Darstellung wie die Achsenkreuze, die Stacheln und die Beschriftungen manchmal unnötig:
sns.kdeplot(diamond_prices, color="red")
# Remove the spine from three sides
sns.despine(top=True, right=True, left=True)
# Remove the ticks and ticklabels
plt.xticks([])
plt.yticks([])
plt.ylabel("")
plt.xlabel("")
# Set a title
plt.title("Diamond prices", fontdict=dict(fontsize=20));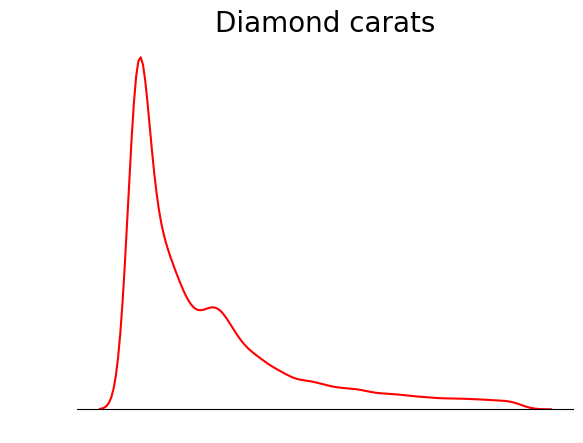
Dieses Grundstück ist viel aufgeräumter. Du kannst die Darstellung weiter verbessern, indem du Linien hinzufügst, die die Position von Mittelwert, Median und Modus kennzeichnen:
sns.kdeplot(diamond_prices, color="red")
sns.despine(top=True, right=True, left=True)
plt.xticks([])
plt.yticks([])
plt.ylabel("")
plt.xlabel("")
plt.title("Diamond prices", fontdict=dict(fontsize=20))
# Find the mean, median, mode
mean_price = diamonds["price"].mean()
median_price = diamonds["price"].median()
mode_price = diamonds["price"].mode().squeeze()
# Add vertical lines at the position of mean, median, mode
plt.axvline(mean_price, label="Mean")
plt.axvline(median_price, color="black", label="Median")
plt.axvline(mode_price, color="green", label="Mode")
plt.legend();
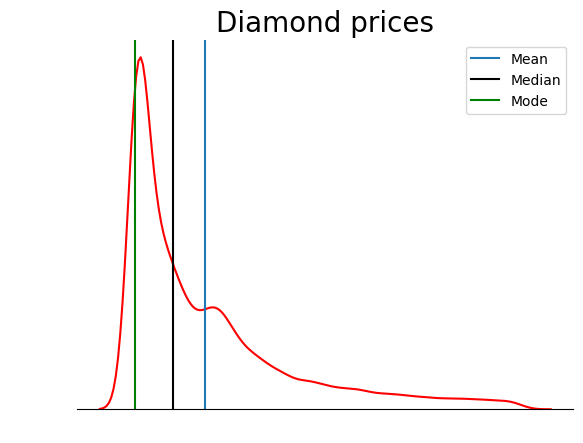
Diese Grafik bestätigt, was wir im Abschnitt über die Arten der Schiefe besprochen haben: Bei einer positiv schiefen Verteilung ist der Mittelwert höher als der Median und der Modus ist niedriger als Mittelwert und Median.
Fazit
Schiefe und Wölbung, die bei der explorativen Datenanalyse oft übersehen werden, geben wichtige Einblicke in die Natur von Verteilungen.
Die Schiefe gibt Aufschluss über die Neigung der Daten, ob sie nun nach links oder rechts tendieren, und zeigt ihre Asymmetrie (falls vorhanden). Ein positiver Schräglauf bedeutet, dass sich der Schwanz nach rechts streckt, während ein negativer Schräglauf in die entgegengesetzte Richtung führt.
Bei der Kurtosis geht es um Spitzen und Schwänze. Eine hohe Kurtosis verstärkt die Spitzen und beschwert die Schwänze, während eine niedrige Kurtosis die Daten streut und die Schwänze aufhellt.
Wenn du mehr über Schiefe und Kurtosis erfahren möchtest, kannst du dir diese hervorragenden Kurse zur quantitativen Analyse ansehen, die von Branchenexperten auf DataCamp angeboten werden:

Ich bin ein Data Science Content Creator mit über 2 Jahren Erfahrung und einem der größten Follower auf Medium. Ich schreibe gerne ausführliche Artikel über KI und ML mit einem etwas sarkastischen Stil, denn man muss etwas tun, damit sie nicht so langweilig sind. Ich habe mehr als 130 Artikel verfasst und einen DataCamp-Kurs gemacht, ein weiterer ist in Vorbereitung. Meine Inhalte wurden von über 5 Millionen Augenpaaren gesehen, von denen 20.000 zu Followern auf Medium und LinkedIn wurden.