Depois de coletar dados e passar horas limpando-os, você pode finalmente começar a explorar! Esse estágio, geralmente chamado de Análise Exploratória de Dados (EDA), talvez seja a etapa mais importante em um projeto de dados. As percepções obtidas com a EDA afetam tudo no futuro.

Por exemplo, uma das etapas obrigatórias na EDA é verificar as formas das distribuições. A identificação correta da forma influencia muitas decisões posteriores no projeto, tais como

• Outras etapas de pré-processamento
• Realizar ou não a detecção e, talvez, a remoção de outliers
• Etapas de transformação ou dimensionamento de recursos
• Seleção de recursos
• Seleção do algoritmo

e assim por diante. Embora existam recursos visuais para realizar a tarefa, você precisa de métricas mais confiáveis para quantificar várias características das distribuições. Duas dessas métricas são a assimetria e a curtose. Você pode usá-las para avaliar a semelhança entre suas distribuições e uma distribuição normal perfeita.

Ao terminar este artigo, você aprenderá em detalhes:

• O que são a assimetria e a curtose
• Os tipos de assimetria e curtose
• O efeito da assimetria e da curtose nos modelos de aprendizado de máquina
• Cálculo da assimetria e da curtose em Python manualmente e com pacotes de terceiros
• Visualização de distribuições para verificar as pontuações de assimetria e curtose (seção abrangente e divertida)

Vamos começar!

O que é Skewness?

Vemos a distribuição normal em todos os lugares: medidas do corpo humano, pesos de objetos, pontuações de QI, resultados de testes ou até mesmo na academia:

Fonte

Além de ser a distribuição favorita da natureza, ela é universalmente apreciada por quase todos os algoritmos de aprendizado de máquina. Enquanto alguns querem que ele melhore e estabilize seu desempenho, outros se recusam terminantemente a trabalhar bem com qualquer coisa que não seja uma distribuição normal (estou falando com vocês, modelos lineares).

Portanto, para satisfazer a necessidade de normalidade dos algoritmos, precisamos de uma maneira de medir a semelhança (ou dissemelhança) de nossas próprias distribuições em relação à curva perfeita em forma de sino.

Vamos começar com as caudas. Em uma distribuição normal perfeita, as caudas são iguais em comprimento. No entanto, quando há assimetria entre as caudas, dando a ela uma aparência inclinada e esmagada para um lado, dizemos que ela está inclinada. E você adivinhou, medimos a extensão dessa assimetria com a assimetria.

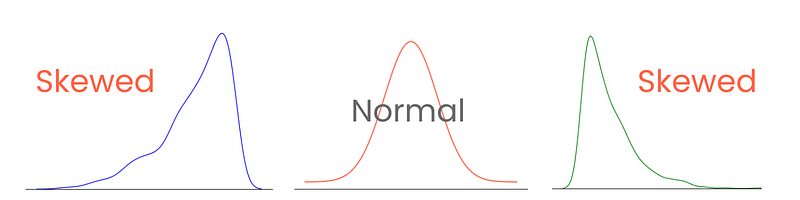
A categorização e a medição corretas da assimetria fornecem percepções sobre como os valores são distribuídos em torno da média e influenciam as escolhas de técnicas estatísticas e transformações de dados. Por exemplo, as distribuições altamente distorcidas podem se beneficiar de técnicas de normalização ou dimensionamento para que se assemelhem à distribuição normal. Isso ajudaria no desempenho do modelo.

Tipos de assimetria

Há três tipos de assimetria: assimetria positiva, negativa e zero.

Vamos começar com a última. Uma distribuição com skewness zero tem as seguintes características:

• Distribuição simétrica com valores uniformemente centralizados em torno da média.
• Não há inclinação, inclinação ou cauda para nenhum dos lados.
• A média, a mediana e a moda estão todas no ponto central.

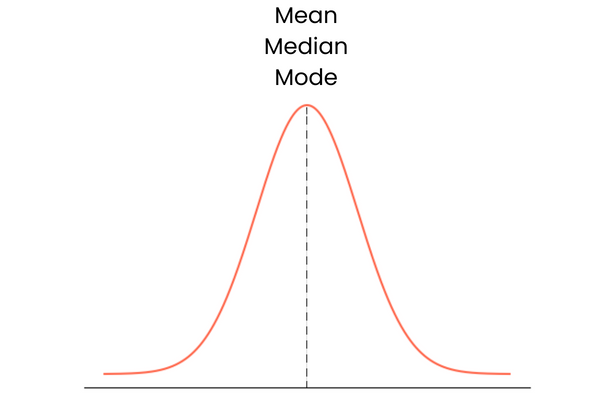
Na prática, a média, a mediana e a moda podem não formar uma linha reta sobreposta perfeita. Eles podem estar um pouco distantes um do outro, mas a diferença seria muito pequena para ter importância.

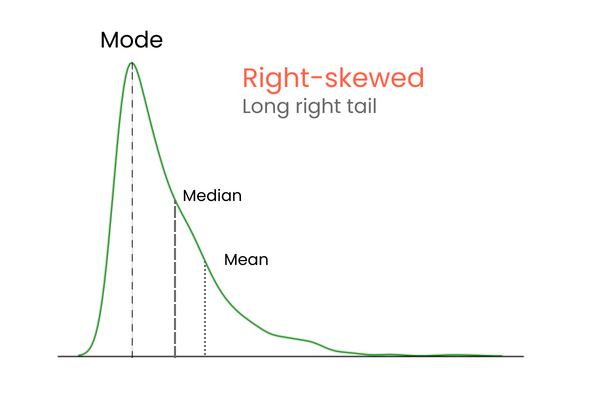
Em uma distribuição com distorção positiva (distorção à direita):

• A cauda direita da distribuição é mais longa ou mais gorda do que a esquerda.
• A média é maior que a mediana, e a moda é menor que a média e a mediana.
• Os valores mais baixos estão agrupados na "colina" da distribuição, enquanto os valores extremos estão na longa cauda direita.
• Também é conhecida como distribuição enviesada à direita.

Em uma distribuição com distorção negativa (distorção à esquerda):

• A cauda esquerda da distribuição é mais longa ou mais gorda do que a direita.
• A média é menor que a mediana, e a moda é maior que a média e a mediana.
• Os valores mais altos estão agrupados na "colina" da distribuição, enquanto os valores extremos estão na longa cauda esquerda.
• Ela também é conhecida como distribuição enviesada à esquerda.

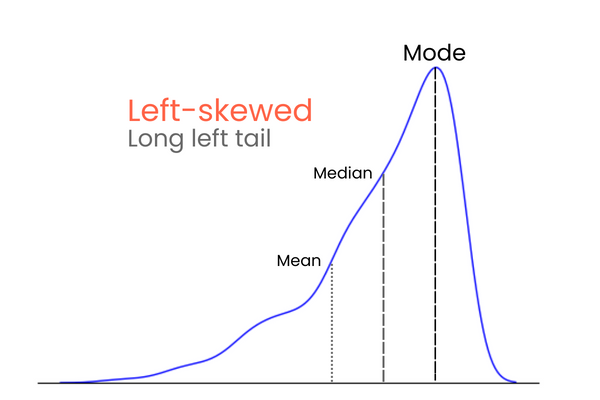
Para lembrar as diferenças entre a assimetria positiva e negativa, pense da seguinte forma: se quiser aumentar a média de uma distribuição, você deve adicionar valores muito mais altos do que a média à distribuição. Para diminuir a média, você deve fazer o oposto: introduzir valores muito mais baixos do que a média na distribuição. Portanto, se a maioria dos valores extremos for maior que a média, a assimetria será positiva porque eles aumentam a média. Se a maioria dos valores extremos for menor do que a média, a assimetria é negativa porque eles diminuem a média.

Como calcular a assimetria em Python

Há muitas maneiras de calcular a assimetria, mas a mais simples é o segundo coeficiente de assimetria de Pearson, também conhecido como assimetria mediana.

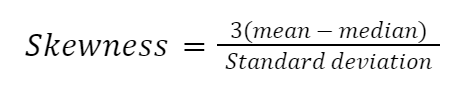
Vamos implementar a fórmula manualmente em Python:

import numpy as np
import pandas as pd
import seaborn as sns

# Example dataset
diamonds = sns.load_dataset("diamonds")
diamond_prices = diamonds["price"]

mean_price = diamond_prices.mean()
median_price = diamond_prices.median()
std = diamond_prices.std()

skewness = (3 * (mean_price - median_price)) / std

>>> print(
   f"The Pierson's second skewness score of diamond prices distribution is {skewness:.5f}"
)

The Pierson's second skewness score of diamond prices distribution is 1.15189

Outra fórmula altamente influenciada pelos trabalhos de Karl Pearson é a fórmula baseada em momentos para aproximar a assimetria. Ele é mais confiável e é dado da seguinte forma:

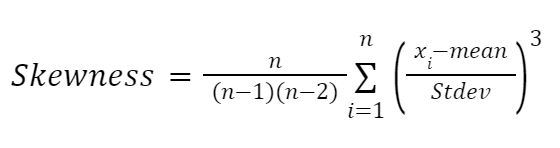
Aqui:

• n representa o número de valores em uma distribuição
• x_i representa cada ponto de dados

Vamos implementá-lo em Python também:

def moment_based_skew(distribution):
   n = len(distribution)
   mean = np.mean(distribution)
   std = np.std(distribution)

   # Divide the formula into two parts
   first_part = n / ((n - 1) * (n - 2))
   second_part = np.sum(((distribution - mean) / std) ** 3)

   skewness = first_part * second_part

   return skewness

>>> moment_based_skew(diamond_prices)
1.618440289857168

Se você não quiser calcular a assimetria manualmente (como eu), poderá usar os métodos incorporados de pandas ou scipy:

# Pandas version
diamond_prices.skew()
1.618395283383529

# SciPy version
from scipy.stats import skew

skew(diamond_prices)
1.6183502776053016

Embora todas as fórmulas para aproximar a assimetria retornem pontuações diferentes, suas diferenças são muito pequenas para serem significativas ou alterar a categorização da assimetria. Por exemplo, todos os métodos que usamos hoje utilizam fórmulas diferentes, mas os resultados são muito próximos.

Depois de calcular a assimetria, você pode categorizar a extensão da assimetria:

• (-0,5, 0,5) - baixa ou aproximadamente simétrica.
• (-1, -0,5) U (0,5, 1) - moderadamente inclinado.
• Além de -1 e 1 - altamente distorcido.

O que é curtose e seus tipos?

Enquanto a assimetria se concentra na dispersão (caudas) da distribuição normal, a curtose se concentra mais na altura. Ele nos diz o quanto nossa distribuição normal (ou semelhante à normal) é plana ou com picos. O termo, que significa curvo ou arqueado em grego, foi cunhado pela primeira vez, sem surpresa, pelo matemático britânico Karl Pearson (ele passou a vida estudando distribuições de probabilidade).

Curtose alta indica:

• Pico acentuado no centro da distribuição.
• Mais valores concentrados em torno da média do que a distribuição normal.
• Caudas mais pesadas devido a uma maior concentração de valores extremos ou discrepantes nas caudas.
• Maior probabilidade de eventos extremos.

Por outro lado, a baixa curtose indica:

• Pico plano.
• Menos valores concentrados em torno da média, mas ainda assim mais do que a distribuição normal.
• Caudas mais leves.
• Menor probabilidade de eventos extremos.

Dependendo do grau, as distribuições têm três tipos de curtose:

1. Distribuição mesocúrtica (curtose = 3, excesso de curtose = 0): distribuição normal perfeita ou muito próxima disso.
2. Distribuição leptocúrtica (curtose > 3, excesso de curtose > 0): pico acentuado, caudas pesadas
3. Distribuição platicúrtica (curtose < 3, excesso de curtose < 0): pico plano, caudas leves

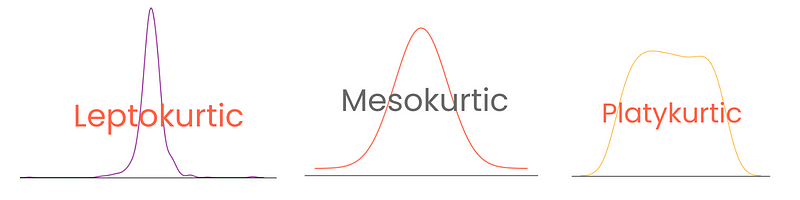
Observe que, aqui, a curtose excessiva é definida como curtose - 3, tratando a curtose da distribuição normal como 0. Dessa forma, os escores de curtose são mais interpretáveis.

Como calcular a curtose em Python

Você pode calcular a curtose em Python da mesma forma que a assimetria usando pandas ou SciPy:

from scipy.stats import kurtosis

kurtosis(diamond_prices)
2.177382669056634

O Pandas oferece duas funções para curtose: kurt e kurtosis. O primeiro é exclusivo para Pandas Series, enquanto o outro pode ser usado em DataFrames.

diamond_prices.kurt()
2.17769575924869

# Select numeric features and calculate kurtosis
diamonds.select_dtypes(include="number").kurtosis()
carat     1.256635
depth     5.739415
table     2.801857
price     2.177696
x        -0.618161
y        91.214557
z        47.086619
dtype: float64

Novamente, os números diferem para a distribuição porque o pandas e o SciPy usam fórmulas diferentes.

Se quiser fazer um cálculo manual da curtose, você pode usar a seguinte fórmula:

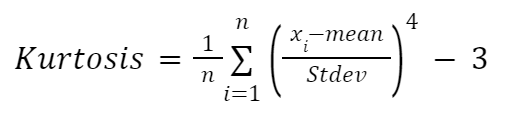
Aqui:

• n representa o número de observações no conjunto de dados
• x_i representa cada ponto de dados individual

Implementaremos a fórmula dentro de uma função novamente:

def moment_based_kurtosis(distribution):
   n = len(distribution)
   mean = np.mean(distribution)
   std = np.std(distribution)

   kurtosis = (1 / n) * sum(((distribution - mean) / std) ** 4) - 3

   return kurtosis

>>> moment_based_kurtosis(diamond_prices)
2.1773826690576463

E descobrimos que os preços dos diamantes têm uma curtose excessiva de 2,18, o que significa que, se traçarmos a distribuição, ela terá um pico mais acentuado do que uma distribuição normal.

Então, vamos fazer isso!

Visualizando a assimetria e a curtose em Python

Um dos melhores recursos visuais para ver a forma e, portanto, a assimetria e a curtose das distribuições é um gráfico de estimativa de densidade de kernel (KDE). Ele está disponível para uso por meio da Seaborn:

import matplotlib.pyplot as plt

sns.kdeplot(diamond_prices)

plt.title("KDE plot of diamond prices")
plt.xlabel("Price ($)")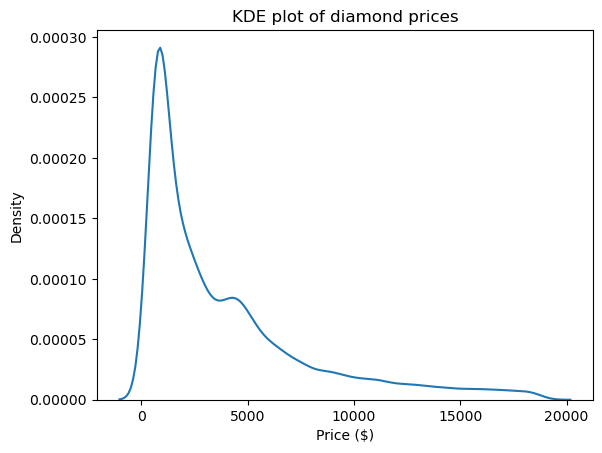

Esse gráfico está de acordo com os números que vimos até este ponto: a distribuição tem uma longa cauda direita, indicando uma assimetria positiva, e tem um pico muito acentuado, que corresponde a uma curtose alta.

O KDE não é o único gráfico a ver a forma. Também podemos usar histogramas:

sns.histplot(diamonds["carat"])

plt.xlabel("Carat")
plt.title("A histogram of the carat of diamonds")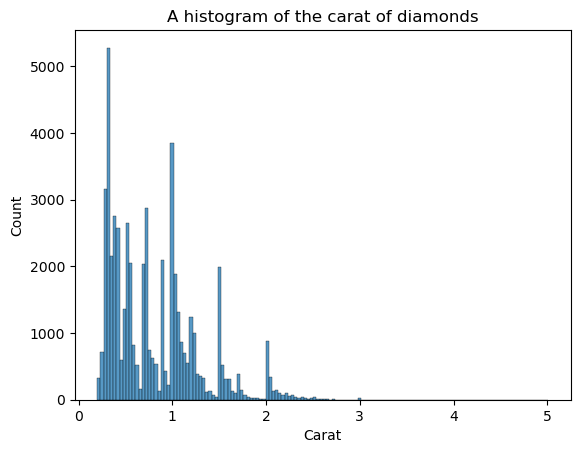

A desvantagem dos histogramas é que você mesmo precisa escolher o número de compartimentos (a contagem de barras). Aqui, há muitas barras que criam ruído no visual - não é possível definir claramente a forma. Então, vamos diminuir o número de compartimentos:

sns.histplot(diamonds["carat"], bins=25)

plt.xlabel("Carat")
plt.title("A histogram of the carat of diamonds")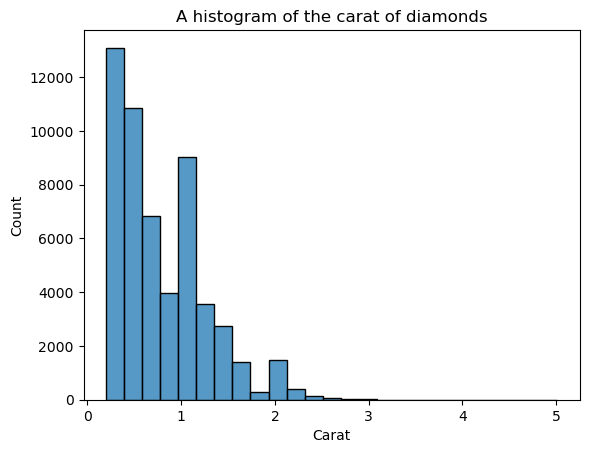

Agora, a forma está mais bem definida, mas podemos aprimorá-la ainda mais. Ao definir kde=True dentro de histplot, podemos traçar um KDE da distribuição na parte superior das barras:

sns.histplot(diamonds["carat"], bins=25, kde=True)

plt.xlabel("Carat")
plt.title("A histogram of the carat of diamonds")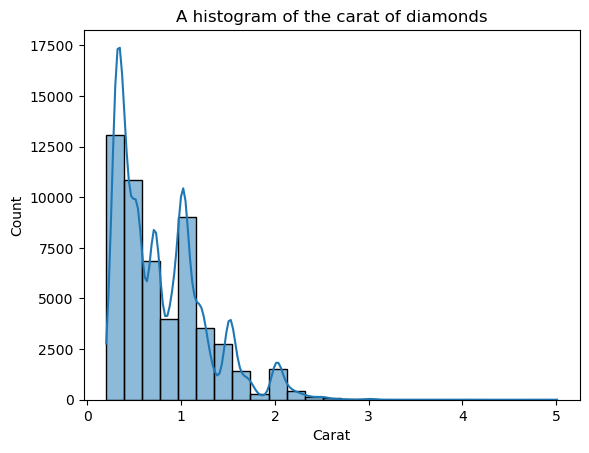

A linha do KDE sobreposta parece irregular, e não a curva suave que nos permite ver a forma geral. O motivo da irregularidade é o fato de a distribuição de quilates ser naturalmente pontiaguda e distante da distribuição normal.

Porém, podemos diminuir a sensibilidade do KDE a essas flutuações ajustando a largura de banda. Isso é feito usando o parâmetro bw_adjust, cujo padrão é 1:

# Change the bandwidth from 1 to 3
sns.kdeplot(diamonds["carat"], bw_adjust=3, color="red")

plt.title("KDE of diamond carats");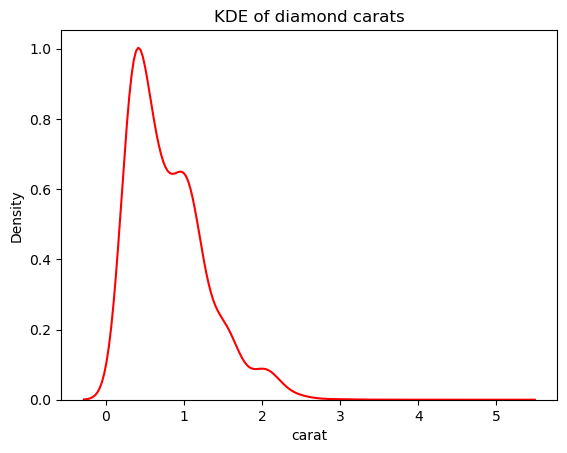

Essa versão parece muito menos espinhosa do que o gráfico do KDE sobreposto. Para ajustar a largura de banda do KDE ao usar um histograma sobreposto a um KDE, você pode usar o parâmetro kde_kws:

ax = sns.histplot(
   diamonds["carat"],
   kde=True,
   kde_kws=dict(bw_adjust=3),
   bins=25,
)

plt.title("An overlaid histogram of diamond carats");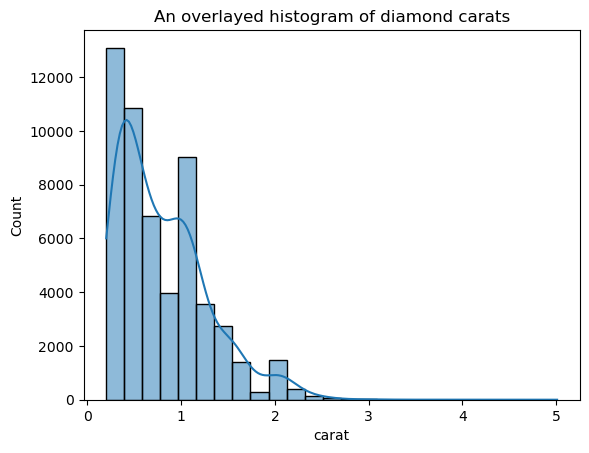

kde_kws aceita qualquer parâmetro que seja aceitável pela função kdeplot que controla o cálculo do KDE.

Um truque que você pode usar ao plotar KDEs é remover tudo, exceto a linha do KDE. Como o objetivo principal de um KDE é ver a forma da distribuição, outros detalhes do gráfico, como os ticks dos eixos, as espinhas e os rótulos, às vezes são desnecessários:

sns.kdeplot(diamond_prices, color="red")

# Remove the spine from three sides
sns.despine(top=True, right=True, left=True)

# Remove the ticks and ticklabels
plt.xticks([])
plt.yticks([])
plt.ylabel("")
plt.xlabel("")

# Set a title
plt.title("Diamond prices", fontdict=dict(fontsize=20));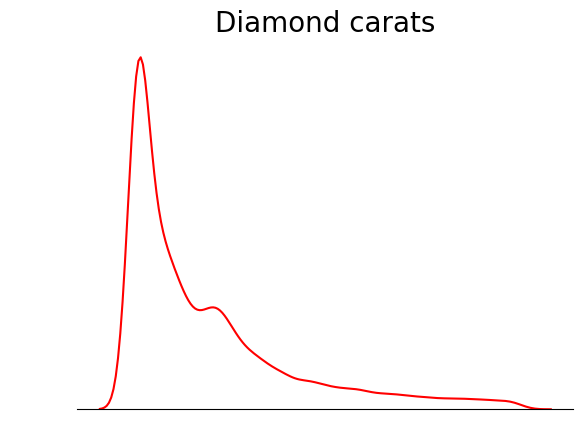

Essa trama é muito mais organizada. Você pode melhorar ainda mais o gráfico adicionando linhas para indicar a posição da média, mediana e moda:

sns.kdeplot(diamond_prices, color="red")

sns.despine(top=True, right=True, left=True)
plt.xticks([])
plt.yticks([])
plt.ylabel("")
plt.xlabel("")
plt.title("Diamond prices", fontdict=dict(fontsize=20))

# Find the mean, median, mode
mean_price = diamonds["price"].mean()
median_price = diamonds["price"].median()
mode_price = diamonds["price"].mode().squeeze()

# Add vertical lines at the position of mean, median, mode
plt.axvline(mean_price, label="Mean")
plt.axvline(median_price, color="black", label="Median")
plt.axvline(mode_price, color="green", label="Mode")

plt.legend();

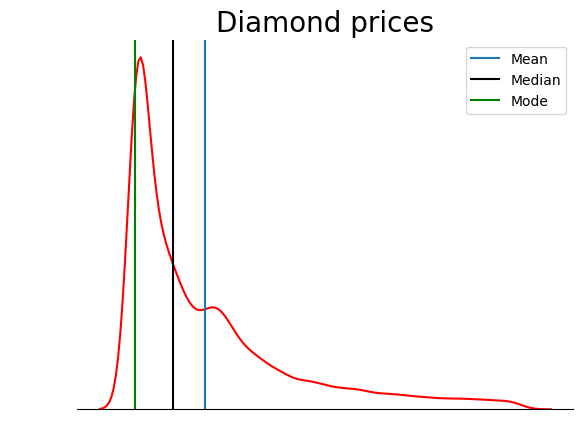
Esse gráfico confirma o que discutimos na seção sobre tipos de assimetria: em uma distribuição com assimetria positiva, a média é maior que a mediana e a moda é menor que a média e a mediana.

Conclusão

A assimetria e a curtose, muitas vezes negligenciadas na Análise Exploratória de Dados, revelam percepções significativas sobre a natureza das distribuições.

A assimetria indica a inclinação dos dados, seja para a esquerda ou para a direita, revelando sua assimetria (se houver). A inclinação positiva significa uma cauda que se estende para a direita, enquanto a inclinação negativa se inclina na direção oposta.

A curtose tem tudo a ver com picos e caudas. A curtose alta acentua os picos e reduz as caudas, enquanto a curtose baixa espalha os dados, aliviando as caudas.

Se quiser saber mais sobre assimetria e curtose, confira estes excelentes cursos de análise quantitativa ministrados por especialistas do setor no DataCamp:

• Gerenciamento de risco de portfólio em Python
• Introdução à análise de portfólio em Python