Curso
As técnicas de classificação são uma parte essencial dos aplicativos de aprendizado de máquina e mineração de dados. Aproximadamente 70% dos problemas em ciência de dados são problemas de classificação. Há muitos problemas de classificação disponíveis, mas a regressão logística é comum e é um método de regressão útil para resolver o problema de classificação binária. Outra categoria de classificação é a classificação multinomial, que lida com os problemas em que várias classes estão presentes na variável de destino. Por exemplo, o conjunto de dados IRIS é um exemplo muito famoso de classificação multiclasse. Outros exemplos são a classificação de categorias de artigos/blogs/documentos.
A regressão logística pode ser usada para vários problemas de classificação, como a detecção de spam. Previsão de diabetes, se um determinado cliente comprará um produto específico ou se irá procurar outro concorrente, se o usuário clicará em um determinado link de anúncio ou não, e muitos outros exemplos.
A regressão logística é um dos algoritmos de aprendizado de máquina mais simples e comumente usados para classificação de duas classes. Ele é fácil de implementar e pode ser usado como linha de base para qualquer problema de classificação binária. Seus conceitos básicos fundamentais também são construtivos na aprendizagem profunda. A regressão logística descreve e estima a relação entre uma variável binária dependente e as variáveis independentes.
Pratique Regressão Logística em Python com este exercício prático.
O que é regressão logística?
A regressão logística é um método estatístico para prever classes binárias. A variável de resultado ou alvo é dicotômica por natureza. Dicotômico significa que há apenas duas classes possíveis. Por exemplo, ele pode ser usado para problemas de detecção de câncer. Ele calcula a probabilidade de ocorrência de um evento.
É um caso especial de regressão linear em que a variável-alvo é de natureza categórica. Ele usa um log de probabilidades como variável dependente. A regressão logística prevê a probabilidade de ocorrência de um evento binário utilizando uma função logit.
Equação de regressão linear:

Onde y é uma variável dependente e x1, x2 ... e Xn são variáveis explicativas.
Função sigmoide:
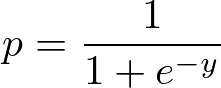
Aplique a função Sigmoid na regressão linear:
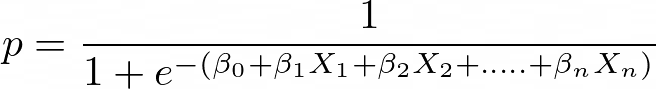
Propriedades da regressão logística:
- A variável dependente na regressão logística segue a distribuição de Bernoulli.
- A estimativa é feita por meio da máxima verossimilhança.
- Sem R Square, a adequação do modelo é calculada por meio de Concordância, KS-Statistics.
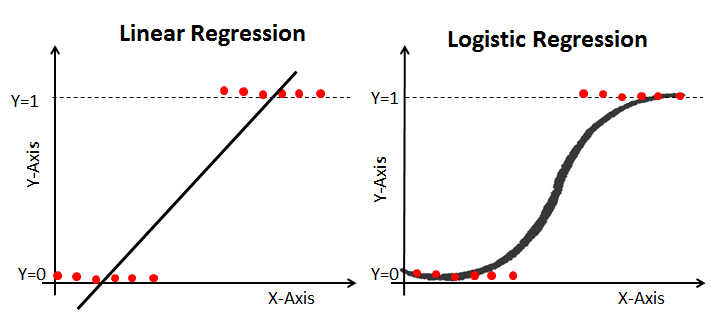
Regressão linear versus regressão linear. Regressão logística
A regressão linear fornece um resultado contínuo, mas a regressão logística fornece um resultado constante. Um exemplo de saída contínua é o preço da casa e o preço das ações. Exemplos de resultados discretos são: prever se um paciente tem câncer ou não, prever se o cliente vai se desligar. A regressão linear é estimada com o uso de mínimos quadrados ordinários (OLS), enquanto a regressão logística é estimada com a abordagem de estimativa de máxima verossimilhança (MLE).
Estimativa de máxima verossimilhança versus estimativa de máxima verossimilhança. Método dos mínimos quadrados
O MLE é um método de maximização da "probabilidade", enquanto o OLS é um método de aproximação com minimização de distância. A maximização da função de verossimilhança determina os parâmetros que têm maior probabilidade de produzir os dados observados. Do ponto de vista estatístico, o MLE define a média e a variação como parâmetros para determinar os valores paramétricos específicos de um determinado modelo. Esse conjunto de parâmetros pode ser usado para prever os dados necessários em uma distribuição normal.
As estimativas de mínimos quadrados ordinários são calculadas ajustando-se uma linha de regressão em determinados pontos de dados que tenham a soma mínima dos desvios quadrados (erro de mínimos quadrados). Ambos são usados para estimar os parâmetros de um modelo de regressão linear. O MLE pressupõe uma função de massa de probabilidade conjunta, enquanto o OLS não exige nenhuma suposição estocástica para minimizar a distância.
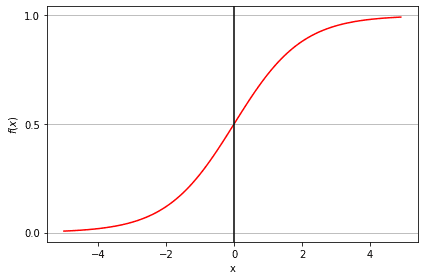
Função sigmoide
A função sigmoide, também chamada de função logística, fornece uma curva em forma de "S" que pode pegar qualquer número de valor real e mapeá-lo em um valor entre 0 e 1. Se a curva for para o infinito positivo, y previsto se tornará 1, e se a curva for para o infinito negativo, y previsto se tornará 0. Se a saída da função sigmoide for maior que 0,5, podemos classificar o resultado como 1 ou SIM, e se for menor que 0,5, podemos classificá-lo como 0 ou NÃO. A saída não pode, por exemplo: Se o resultado for 0,75, podemos dizer em termos de probabilidade que: Há uma chance de 75% de que um paciente sofra de câncer.

Tipos de regressão logística
Tipos de regressão logística:
- Regressão logística binária: A variável-alvo tem apenas dois resultados possíveis, como Spam ou Não Spam, Câncer ou Não Câncer.
- Regressão logística multinomial: A variável-alvo tem três ou mais categorias nominais, como a previsão do tipo de vinho.
- Regressão logística ordinal: a variável-alvo tem três ou mais categorias ordinais, como a classificação de um restaurante ou produto de 1 a 5.
Execute e edite o código deste tutorial online
Executar códigoCriação de modelos no Scikit-learn
Vamos criar o modelo de previsão de diabetes.
Aqui, você vai prever o diabetes usando o Classificador de Regressão Logística.
Primeiro, vamos carregar o conjunto de dados necessário do Pima Indian Diabetes usando a função CSV de leitura do pandas. Você pode fazer o download dos dados no seguinte link: https://www.kaggle.com/uciml/pima-indians-diabetes-database ou selecionar um conjunto de dados no DataCamp: https://www.datacamp.com/workspace/datasets. O conjunto de dados pronto para uso oferece a opção de treinar o modelo no DataCamp's Workspace, que é um notebook Jupyter gratuito na nuvem.
Carregando dados
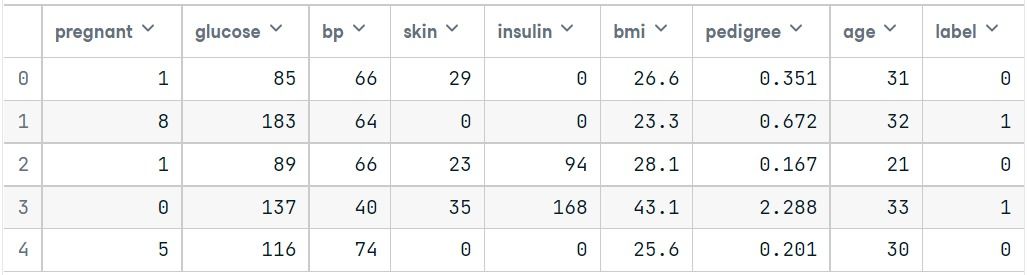
Simplificaremos as colunas fornecendo col_names à função read_csv() do pandas.
#import pandas
import pandas as pd
col_names = ['pregnant', 'glucose', 'bp', 'skin', 'insulin', 'bmi', 'pedigree', 'age', 'label']
# load dataset
pima = pd.read_csv("pima-indians-diabetes.csv", header=None, names=col_names)pima.head()Seleção de recurso
Aqui, você precisa dividir as colunas fornecidas em dois tipos de variáveis: dependente (ou variável-alvo) e independente (ou variáveis de recursos).
#split dataset in features and target variable
feature_cols = ['pregnant', 'insulin', 'bmi', 'age','glucose','bp','pedigree']
X = pima[feature_cols] # Features
y = pima.label # Target variableDivisão de dados
Para entender o desempenho do modelo, dividir o conjunto de dados em um conjunto de treinamento e um conjunto de teste é uma boa estratégia.
Vamos dividir o conjunto de dados usando a função train_test_split(). Você precisa passar 3 parâmetros: recursos, alvo e tamanho do conjunto de teste. Além disso, é possível usar random_state para selecionar registros aleatoriamente.
# split X and y into training and testing sets
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=16)Aqui, o conjunto de dados é dividido em duas partes em uma proporção de 75:25. Isso significa que 75% dos dados serão usados para o treinamento do modelo e 25% para o teste do modelo.
Desenvolvimento e previsão de modelos
Primeiro, importe o módulo Logistic Regression e crie um objeto classificador de Logistic Regression usando a função LogisticRegression() com random_state para reprodutibilidade.
Em seguida, ajuste seu modelo no conjunto de treinamento usando fit() e faça a previsão no conjunto de teste usando predict().
# import the class
from sklearn.linear_model import LogisticRegression
# instantiate the model (using the default parameters)
logreg = LogisticRegression(random_state=16)
# fit the model with data
logreg.fit(X_train, y_train)
y_pred = logreg.predict(X_test)Avaliação do modelo usando a matriz de confusão
Uma matriz de confusão é uma tabela usada para avaliar o desempenho de um modelo de classificação. Você também pode visualizar o desempenho de um algoritmo. O fundamental de uma matriz de confusão é o número de previsões corretas e incorretas somadas por classe.
# import the metrics class
from sklearn import metrics
cnf_matrix = metrics.confusion_matrix(y_test, y_pred)
cnf_matrixarray([[115, 8],
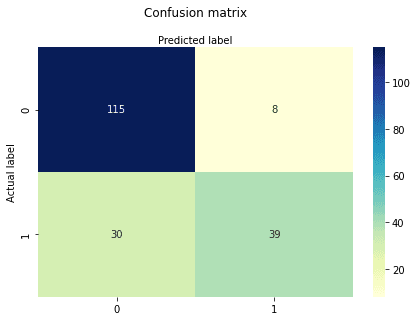
[ 30, 39]])Aqui, você pode ver a matriz de confusão na forma de um objeto de matriz. A dimensão dessa matriz é 2*2 porque esse modelo é de classificação binária. Você tem duas classes 0 e 1. Os valores diagonais representam previsões precisas, enquanto os elementos não diagonais são previsões imprecisas. No resultado, 115 e 39 são previsões reais, e 30 e 8 são previsões incorretas.
Visualização da matriz de confusão usando o mapa de calor
Vamos visualizar os resultados do modelo na forma de uma matriz de confusão usando matplotlib e seaborn.
Aqui, você visualizará a matriz de confusão usando o Heatmap.
# import required modules
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
class_names=[0,1] # name of classes
fig, ax = plt.subplots()
tick_marks = np.arange(len(class_names))
plt.xticks(tick_marks, class_names)
plt.yticks(tick_marks, class_names)
# create heatmap
sns.heatmap(pd.DataFrame(cnf_matrix), annot=True, cmap="YlGnBu" ,fmt='g')
ax.xaxis.set_label_position("top")
plt.tight_layout()
plt.title('Confusion matrix', y=1.1)
plt.ylabel('Actual label')
plt.xlabel('Predicted label')
Text(0.5,257.44,'Predicted label');Métricas de avaliação da matriz de confusão
Vamos avaliar o modelo usando o classification_report para obter exatidão, precisão e recuperação.
from sklearn.metrics import classification_report
target_names = ['without diabetes', 'with diabetes']
print(classification_report(y_test, y_pred, target_names=target_names)) precision recall f1-score support
without diabetes 0.79 0.93 0.86 123
with diabetes 0.83 0.57 0.67 69
accuracy 0.80 192
macro avg 0.81 0.75 0.77 192
weighted avg 0.81 0.80 0.79 192Bem, você obteve uma taxa de classificação de 80%, considerada uma boa precisão.
Precisão: A precisão tem a ver com ser preciso, ou seja, com a exatidão de seu modelo. Em outras palavras, você pode dizer, quando um modelo faz uma previsão, com que frequência ele está correto. No seu caso de previsão, quando o modelo de regressão logística previu que os pacientes sofreriam de diabetes, os pacientes tiveram 73% das vezes.
Recall: Se houver pacientes com diabetes no conjunto de testes e seu modelo de regressão logística puder identificá-lo em 57% das vezes.
Curva ROC
A curva ROC (Receiver Operating Characteristic, característica operacional do receptor) é um gráfico da taxa de verdadeiros positivos em relação à taxa de falsos positivos. Ele mostra a troca entre sensibilidade e especificidade.
y_pred_proba = logreg.predict_proba(X_test)[::,1]
fpr, tpr, _ = metrics.roc_curve(y_test, y_pred_proba)
auc = metrics.roc_auc_score(y_test, y_pred_proba)
plt.plot(fpr,tpr,label="data 1, auc="+str(auc))
plt.legend(loc=4)
plt.show()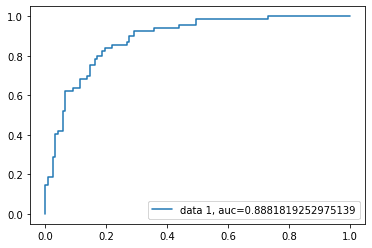
A pontuação AUC para o caso é de 0,88. A pontuação AUC 1 representa um classificador perfeito, e 0,5 representa um classificador inútil.
O código-fonte está disponível no Workspace: Understanding Logistic Regression in Python (Entendendo a regressão logística em Python).
Vantagens
Devido à sua natureza eficiente e direta, ele não exige alta capacidade de computação, é fácil de implementar, facilmente interpretável e amplamente utilizado por analistas de dados e cientistas. Além disso, não requer dimensionamento de recursos. A regressão logística fornece uma pontuação de probabilidade para as observações.
Disadvantages
A regressão logística não é capaz de lidar com um grande número de características/variáveis categóricas. Ele é vulnerável ao ajuste excessivo. Além disso, não é possível resolver o problema não linear com a regressão logística, e é por isso que ela exige uma transformação de recursos não lineares. A regressão logística não terá um bom desempenho com variáveis independentes que não estejam correlacionadas à variável-alvo e que sejam muito semelhantes ou correlacionadas entre si.
Conclusão
Neste tutorial, você abordou muitos detalhes sobre a regressão logística. Você aprendeu o que é regressão logística, como criar os respectivos modelos, como visualizar os resultados e algumas das informações teóricas básicas. Além disso, você abordou alguns conceitos básicos, como a função sigmoide, a máxima verossimilhança, a matriz de confusão e a curva ROC.
Esperamos que agora você possa utilizar a técnica de regressão logística para analisar seus próprios conjuntos de dados. Obrigado por ler este tutorial!
Se você quiser saber mais sobre regressão logística, faça o curso Aprendizado de máquina com scikit-learn do DataCamp. Você também pode começar sua jornada para se tornar um engenheiro de aprendizado de máquina inscrevendo-se na carreira de Cientista de aprendizado de máquina com Python.