Excel Zinseszinsformel: Ein umfassender Leitfaden

Das Verständnis des Zinseszinses ist für die Finanzanalyse von entscheidender Bedeutung, denn er spielt eine wichtige Rolle bei persönlichen Finanzen, Investitionsstrategien und unternehmerischen Entscheidungen. Excel hilft dabei, diese Berechnungen zu vereinfachen und macht es einfacher, zukünftige Ersparnisse zu prognostizieren, Investitionsrenditen zu bewerten und Kreditrückzahlungen zu planen.

Dieser Leitfaden führt dich durch verschiedene Methoden zur Berechnung von Zinseszinsen in Excel, von grundlegenden Formeln bis hin zu fortgeschrittenen Techniken. Unser Finanzmodellierung in Excel baut auf den Techniken und Strategien auf, die in diesem Lernprogramm besprochen werden. Wenn du diese Konzepte beherrschst, kannst du deine Fähigkeiten zur Finanzanalyse deutlich verbessern.

Was ist Zinseszins?

Der Zinseszins steht für das exponentielle Wachstum von Geld im Laufe der Zeit. Im Gegensatz zu einfachen Zinsen, die linear wachsen, beschleunigt sich der Zinseszins, da die in jeder Periode erwirtschafteten Zinsen Teil des Kapitals der nächsten Periode werden.

Die Macht des Zinseszinses wird deutlich, wenn du dir langfristige Investitionen vorstellst. Angenommen, ein kleiner Unterschied bei den Zinssätzen (z. B. 6 % gegenüber 8 %) kann über Jahrzehnte hinweg zu dramatisch unterschiedlichen Ergebnissen führen, die den Unterschied zwischen einem komfortablen Ruhestand und finanziellen Schwierigkeiten ausmachen können.

Die Zinseszinsformel

Der Zinseszins wird mit der Formel berechnet:

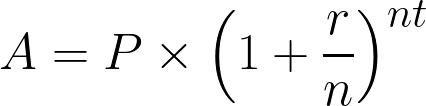
Zinseszinsformel. Bild vom Autor.

Wo:

• A = Endbetrag nach Zinsen
• P = Kapital (Anfangsinvestition)
• r = Jährlicher Zinssatz (in dezimaler Form)
• n = Anzahl der Zinseszinszahlungen pro Jahr
• t = Anzahl der Jahre

Nachdem wir nun das Konzept und die mathematische Formel verstanden haben, wollen wir sie in Excel implementieren.

Berechnung von Zinseszinsen in Excel

Um diese Formel in Excel umzusetzen, erstellst du eine einfache Tabellenstruktur mit deutlich beschrifteten Zellen für jede Variable.

Gliedere dein Arbeitsblatt zunächst mit den folgenden Bezeichnungen:

• Cell A1: "Schulleiter"
• Cell A2: "Jährlicher Zinssatz"
• Zelle A3: "Compounding Perioden pro Jahr"
• Zelle A4: "Zeit (Jahre)"
• Zelle A5: "Endbetrag"

Als nächstes trägst du deine Werte in Spalte B ein:

• Cell B1: Gib deinen Hauptbetrag ein (z. B. 1000)

• Zelle B2: Gib deinen Zinssatz als Dezimalzahl ein (z. B. 0.05 für 5%)

• Cell B3: Gib die Anzahl der Aufzinsungsperioden pro Jahr an (z. B. 12 für monatlich)

• Zelle B4: Gib die Zeit in Jahren ein (z.B. 5)

Nach dem Einrichten der Daten sollte deine Excel-Tabelle wie folgt aussehen:

Einrichten der Excel-Tabelle. Bild vom Autor.

Schließlich gibst du in Zelle B5 die Zinseszinsformel ein:

=B1*(1+B2/B3)^(B3*B4)

Zinseszinsformel in Excel. Bild vom Autor.

Diese Formel wendet die obige mathematische Gleichung direkt an und berechnet den Endbetrag nach Zinseszins.

Berechne den Zinseszins. Bild vom Autor.

Verwendung der Funktion FV()

Auch wenn die manuelle Formel gut funktioniert, bietet Excel integrierte Finanzfunktionen, die die Zinseszinsberechnung vereinfachen. Die Funktion FV() (Zukunftswert) ist besonders nützlich für die Berechnung von Zinseszinsen bei regelmäßigen Zahlungen oder Investitionen.

Die Syntax für die Funktion FV() lautet:

=FV(rate, nper, pmt, [pv], [type])

Wo:

• rate = Zinssatz pro Periode

• nper = Gesamtzahl der Zahlungsperioden

• pmt = Zahlung pro Periode (0 eingeben, wenn keine)

• pv = Barwert (anfängliches Kapital), sollte als negative Zahl eingegeben werden

• type = Wann die Zahlungen fällig sind (0 für Ende der Periode, 1 für Anfang)

Ändern wir unser Tabellenblatt, um die Funktion FV() zu verwenden:

• Zelle A6: "Die Funktion FV() verwenden"

Gib das Folgende in Zelle B6 ein:

=FV(B2/B3, B3*B4, 0, -B1)

Zinseszinsberechnung mit FV(). Bild vom Autor.

Beachte, dass wir den jährlichen Zinssatz durch die Anzahl der Zinseszinsperioden teilen, um den Zinssatz pro Periode zu erhalten, und dass wir das Kapital als negative Zahl eingeben, wie es die Funktion verlangt.

Du solltest den berechneten Zinseszins wie unten dargestellt sehen können:

Zinseszinsen mit FV(). Bild vom Autor.

Verwendung der Funktion PMT()

Die Funktion PMT() berechnet die Zahlung für ein Darlehen auf der Grundlage konstanter Zahlungen und eines konstanten Zinssatzes. Es ist zwar in erster Linie für Darlehenszahlungen gedacht, kann aber auch für Zinseszinsszenarien angepasst werden, bei denen du regelmäßige Beitragsbeträge festlegen willst, um eine Zielsumme zu erreichen.

Die Syntax für die Funktion PMT() lautet:

=PMT(rate, nper, pv, [fv], [type])

Wo:

• rate = Zinssatz pro Periode

• nper = Gesamtzahl der Zahlungsperioden

• pv = Barwert (ursprüngliches Kapital)

• fv = Zukünftiger Wert (der Zielbetrag, den du erreichen willst)

• type = Wann die Zahlungen fällig sind (0 für Ende der Periode, 1 für Anfang)

Fügen wir dies zu unserer Tabelle hinzu:

• Zelle A7: "Zielbetrag"

• Zelle B7: Gib deinen Zielbetrag ein (z. B. 5000)

• Zelle A8: "Erforderliche monatliche Zahlung"

Gib Folgendes in Zelle B8 ein:

=PMT(B2/12, B4*12, -B1, B7)

Zinseszinsberechnung mit PMT(). Bild vom Autor.

Diese Formel berechnet, wie viel du monatlich einzahlen musst, um deinen Zielbetrag zu erreichen, wenn du dein Anfangskapital und den Zinssatz berücksichtigst.

Die berechnete monatliche Zahlung ist unten zu sehen:

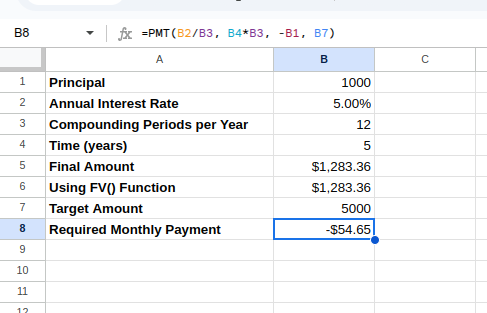
Zinseszinsen mit PMT(). Bild vom Autor.

Die Funktion PMT() in Excel liefert standardmäßig einen negativen Wert, da sie aus der Perspektive des Cashflows entwickelt wurde:

• Negative Werte stehen für Geld, das du auszahlst (Mittelabfluss)
• Positive Werte stehen für Geld, das du erhältst (Geldzufluss)

Excel Zinseszins in Aktion

Die Zinseszinsformel in Excel hat zahlreiche reale Anwendungen in der Finanzwelt und im Geschäftsleben. Lass uns einige dieser praktischen Szenarien untersuchen.

Ersparnisse und Investitionen

Eine der häufigsten Anwendungen von Zinseszinsberechnungen ist die Vorausberechnung des Wachstums von Spar- oder Anlagekonten. Zu verstehen, wie Geld im Laufe der Zeit wächst, kann uns helfen, fundierte Entscheidungen zu treffen.

Lass uns in einem neuen Abschnitt unseres Tabellenblatts ein Modell für die Altersvorsorge erstellen. Nachdem du in Zelle D1 "Rentensparprognose" eingegeben hast, kannst du deine Parameter in den Zellen D2 bis D6 einstellen:

• Cell D2: "Erstinvestition" mit E2: 10000

• Cell D3: "Monatlicher Beitrag" mit E3: 500

• Zelle D4: "Jährlicher Zinssatz" mit E4: 0.07

• Zelle D5: "Zeithorizont (Jahre)" mit E5: 30

• Zelle D6: "Compounding Frequency" mit E6: "Monatlich"

Nachdem du in Zelle D7 den "Voraussichtlichen Zukunftswert" eingegeben hast, gibst du in E7 die folgende Gleichung ein:

=FV(E4/12, E5*12, -E3, -E2)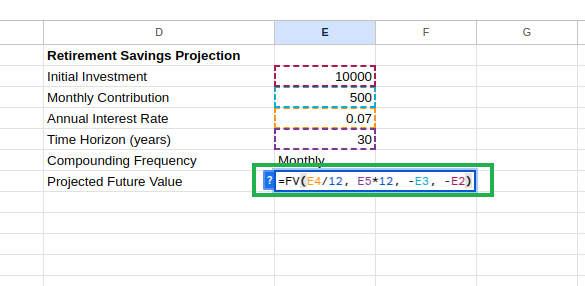

Berechnung des prognostizierten Zukunftswerts. Bild vom Autor.

Diese Formel projiziert deine Rentenersparnisse und berücksichtigt dabei sowohl deine Anfangsinvestition als auch deine regelmäßigen Beiträge. Du kannst den zukünftigen Wert wie unten dargestellt sehen:

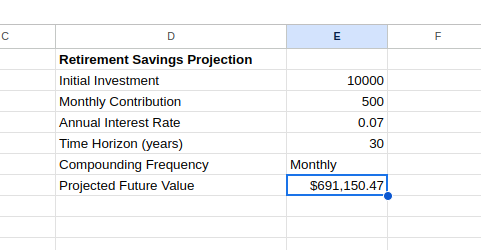
Prognostizierter Zukunftswert mit FV(). Bild vom Autor.

Wir können dieses Modell erweitern, indem wir eine Tabelle für jedes Jahr erstellen:

• Gib in Zelle D9 "Jahr-für-Jahr-Projektion" ein.

• In Zelle D10 gibst du "Jahr" und in Zelle E10 "Saldo" ein.

• In Zelle D11 gibst du 0 (Anfangsjahr) ein.

• In Zelle E11 gibst du deine Anfangsinvestition ein: =E2

• In Zelle D12 gibst du ein 1

• Berechne in Zelle E12 den Saldo nach dem Jahr 1:

=FV($E$4/12, 1*12, -$E$3, -E11)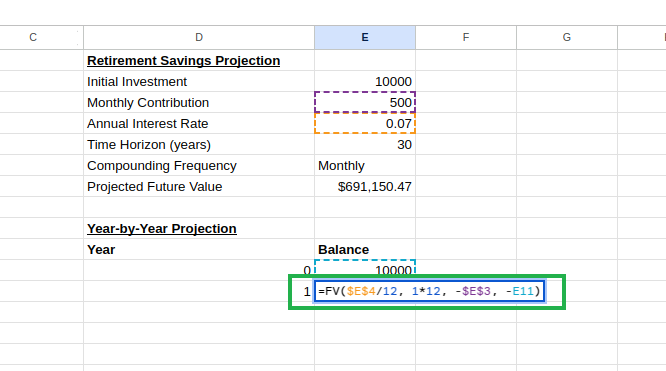

Erstellen einer Tabelle für die Jahresprojektion. Bild vom Autor.

• Wähle die Zellen D11 und D12 aus, dann klicke und ziehe den Füllgriff (kleines Quadrat in der rechten unteren Ecke) nach unten in die Zeile 41, um die Jahre 0 bis 30 zu erstellen
• Wähle die Zelle E12 aus, klicke und ziehe dann den Füllgriff nach unten in die Zeile 41

Excel passt die Zellbezüge in jeder Zeile automatisch an und erstellt eine Reihe von Berechnungen, bei denen jedes Jahr auf dem Saldo des Vorjahres aufbaut.

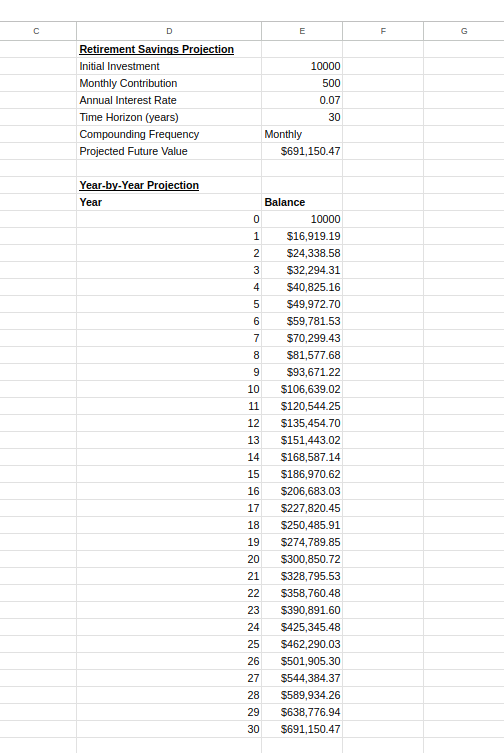
Tabelle mit Jahresprojektionen. Bild vom Autor.

Dieses Diagramm kann dir helfen zu verstehen, wie deine Ersparnisse im Laufe der Zeit wachsen und kann dich motivieren, konsequent zu investieren, indem es das für den Zinseszins typische beschleunigte Wachstumsmuster veranschaulicht.

Darlehensberechnungen

Zinseszins gilt auch für Kredite, bei denen die Zinsen auf den verbleibenden Saldo anfallen. Die Excel-Funktionen können dir helfen, verschiedene Aspekte von Krediten zu verstehen, von den monatlichen Zahlungen bis zu den gezahlten Zinsen.

Um einen Tilgungsplan zu erstellen, stellst du die Parameter deines Kredits wie unten gezeigt ein:

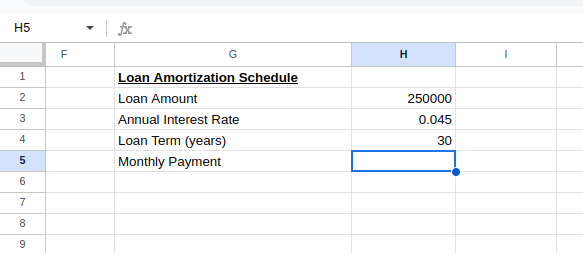Berechne die monatliche Rate für das Darlehen. Bild vom Autor.

Gib in Zelle H3 Folgendes ein, um die monatliche Zahlung zu berechnen:

=PMT(H3/12, H4*12, H2)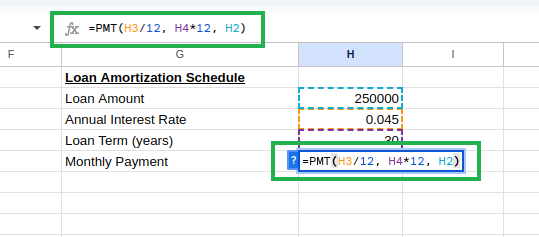

Berechnung der monatlichen Kreditrate mit PMT(). Bild vom Autor.

Du würdest die monatliche Zahlung sehen als:

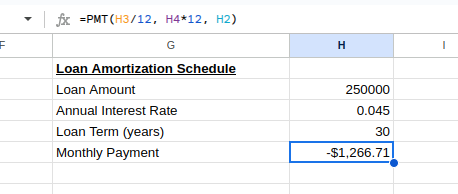
Monatliche Zahlung des Kredits. Bild vom Autor.

Richte als Nächstes die Tabelle für den Tilgungsplan mit einer Kopfzeile ein, wie unten gezeigt:

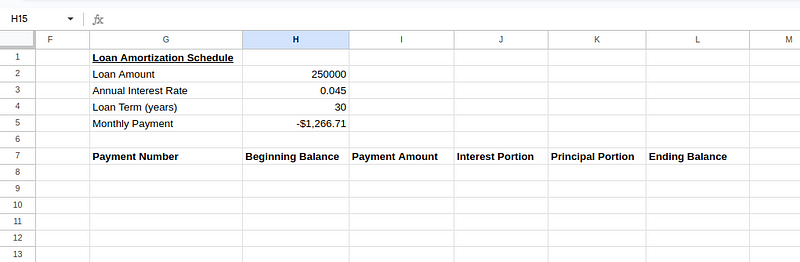Erstellen einer Tabelle mit Tilgungsplänen. Bild vom Autor.

Gib die Anfangswerte für die erste Zahlung ein (Zeile 8):

• Zelle G8: 1 (erste Zahlung)

• Zelle H8: =H2 (ursprünglicher Kreditbetrag)

• Zelle I8: =ABS(H5) (Zahlungsbetrag, unter Verwendung von ABS(), um das negative Ergebnis von PMT() in ein positives umzuwandeln)

• Zelle J8: =H8*($H$3/12) (Zinsanteil: Anfangssaldo × monatliche Rate)

• Zelle K8: =I8-J8 (Hauptteil: Zahlungsbetrag - Zinsanteil)

• Zelle L8: =H8-K8 (Endsaldo: Anfangssaldo - Hauptteil)

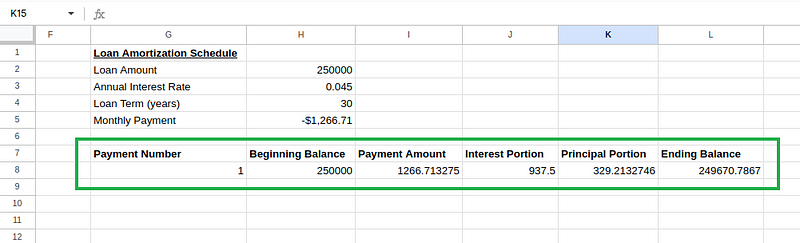Amortisationsplan Tabelle Berechnungen. Bild vom Autor.

Für die zweite Zahlung (Zeile 9) erstellst du die folgenden Formeln:

• Zelle G9: 2 (zweite Zahlung)

• Zelle H9: =L8 (Anfangssaldo ist gleich dem Endsaldo der vorherigen Zahlung)

• Zelle I9: =I8 (der Zahlungsbetrag bleibt gleich)

• Zelle J9: =H9*($H$3/12) (Zinsanteil basierend auf dem neuen Anfangssaldo)

• Zelle K9: =I9-J9 (Hauptteil)

• Zelle L9: =H9-K9 (Endsaldo)

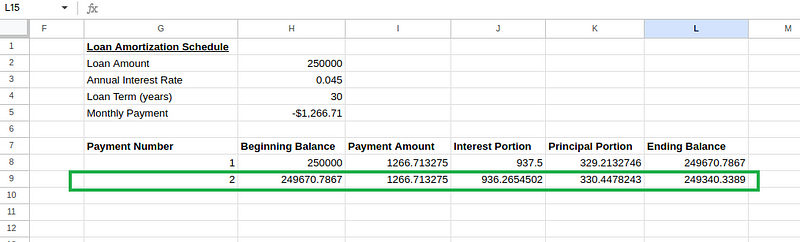Berechnungen von Amortisationstabellen. Bild vom Autor.

Wähle dann die Zellen H9 bis L9 aus und ziehe sie nach unten in die Zeile 367 (für alle 360 Zahlungen).

In Zelle H6 können wir die gesamten gezahlten Zinsen berechnen: 

=SUM(J8:J367)

Der endgültige Zeitplan sollte wie folgt aussehen:

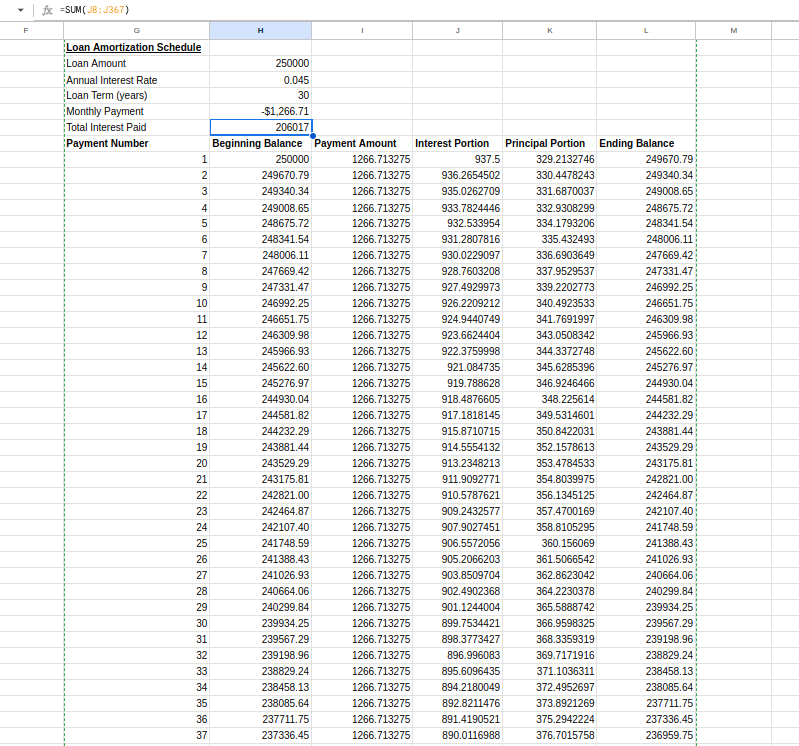Tabelle der Tilgungspläne. Bild vom Autor.

Dieser Tilgungsplan zeigt dir, wie sich jede Zahlung auf deinen Kreditsaldo und die Höhe der Zinsen auswirkt, die du während der Laufzeit deines Kredits zahlst. Frühe Zahlungen decken vor allem die Zinsen ab, während spätere Zahlungen vor allem das Kapital reduzieren - eine wichtige Erkenntnis für das Verständnis von Hypothekendarlehen.

Fortgeschrittene Zinseszins-Techniken

Wir wollen nun Szenarien untersuchen, in denen einige fortgeschrittene Techniken zum Einsatz kommen, z. B. der Umgang mit unregelmäßigen Aufzinsungsperioden und unterschiedlichen Zinssätzen.

Variable Zinssätze

In der realen Welt gibt es oft variable Zinssätze, z. B. bei Hypotheken mit variablem Zinssatz oder bei marktabhängigen Anlagen. Excel kann diese komplexen Szenarien mit einigen zusätzlichen Einstellungen bewältigen.

Wir können ein Modell mit unterschiedlichen Zinssätzen für verschiedene Zeiträume erstellen. Erstellen wir eine Tabelle mit variablen Zinssätzen unter der Annahme, dass die Zinssätze alle 5 Jahre um 0,5 % steigen:

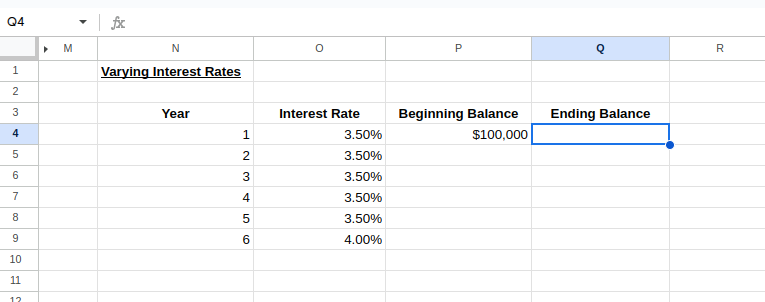Erstelle eine Tabelle für unterschiedliche Zinssätze. Bild vom Autor.

Um den Endsaldo von Jahr 1 und den Anfangssaldo von Jahr 2 zu berechnen, gib Folgendes ein:

• Zelle Q4: =P4*(1+O4)

• Zelle P5: =Q4

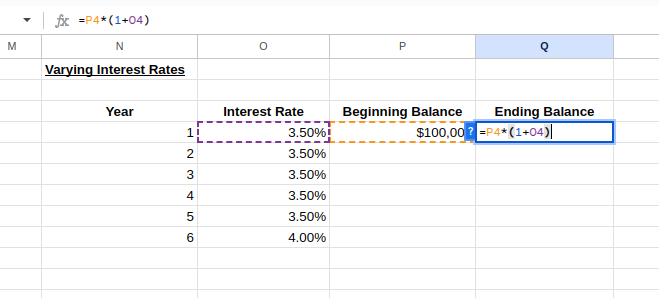Berechnung der variablen Zinssätze. Bild vom Autor.

Wir können nun die Zeilen der Jahre 1-2 markieren und nach unten ziehen, um die Tabelle auf die gewünschte Anzahl von Jahren zu erweitern und die Zinssätze nach Bedarf zu ändern, wie in der folgenden Abbildung zu sehen ist:

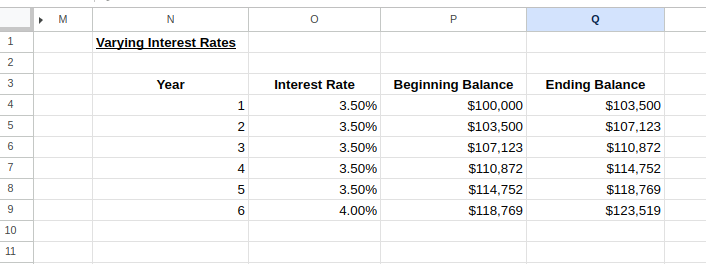Variabler Zinssatz-Rechner. Bild vom Autor.

Mit diesem Modell kannst du dir vorstellen, wie sich veränderte Zinssätze im Laufe der Zeit auf deine Investition oder dein Darlehen auswirken. 

Häufigkeit der Aufstockung

In der realen Welt gibt es bei Finanzprodukten oft nicht standardisierte Zinseszinsperioden. Manche Anlagen werden vierteljährlich aufgezinst, andere monatlich und manche sogar täglich. Diese Unterschiede in der Aufzinsungshäufigkeit können deine Rendite im Laufe der Zeit erheblich beeinflussen.

Um diese Abweichungen in Excel zu berücksichtigen, kannst du die Zinseszinsformel entsprechend anpassen. Angenommen, du berechnest eine Investition von 10.000 $ mit 6 % Zinsen pro Jahr und täglichem Zinseszins für 5 Jahre nach dieser Formel:

=10000*(1+0.06/365)^(365*5)

Ein Beispiel für einen unregelmäßigen Compounding-Rechner sieht so aus:

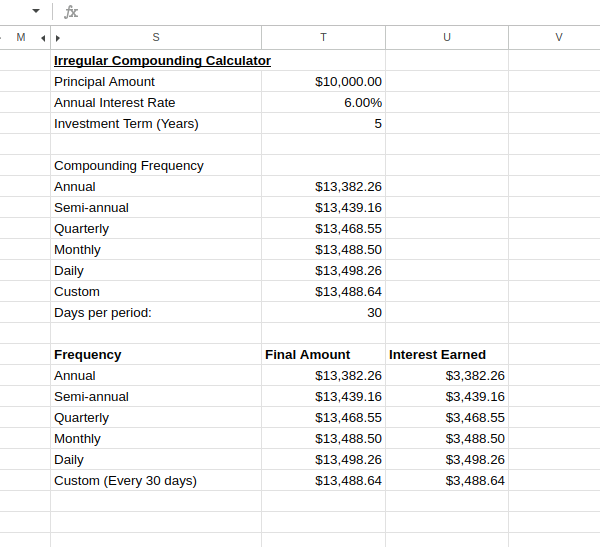Rechner für unregelmäßige Aufzinsung. Bild vom Autor.

Dieser Vergleich zeigt deutlich, wie sich der Zinseszinseffekt auf deine Rendite auswirkt.

Wie du siehst, führt häufigerer Zinseszins zu höheren Erträgen, obwohl der zusätzliche Nutzen mit zunehmender Häufigkeit abnimmt. Diese Erkenntnis ist besonders wertvoll, wenn du Finanzprodukte bewertest, die mit unterschiedlichen Aufzinsungsmethoden werben.

Fazit

In diesem Leitfaden haben wir uns mit verschiedenen praktischen Anwendungen der Zinseszinsformeln von Excel beschäftigt. Vom Verständnis der grundlegenden mathematischen Formeln bis hin zur Implementierung der Excel-Finanzfunktionen wie FV() und PMT() haben wir nun das nötige Rüstzeug, um aussagekräftige Finanzberechnungen durchzuführen.

Wenn du deine Excel-Kenntnisse über dieses Lernprogramm hinaus vertiefen möchtest, solltest du dich für unseren Kurs Finanzmodellierung in Excel Kurs. Dieser Kurs baut auf den im Tutorium besprochenen grundlegenden Konzepten mit fortgeschrittenen Finanzmodellierungstechniken auf.