Fórmula del interés compuesto en Excel: Guía completa

Comprender el interés compuesto es crucial para el análisis financiero, ya que desempeña un papel importante en las finanzas personales, las estrategias de inversión y la toma de decisiones empresariales. Excel ayuda a simplificar estos cálculos, facilitando la previsión de ahorros futuros, la evaluación del rendimiento de las inversiones y la planificación de la amortización de préstamos.

Esta guía te guiará a través de diferentes métodos para calcular el interés compuesto en Excel, desde fórmulas básicas hasta técnicas avanzadas. Nuestra Modelización financiera en Excel se basa en las técnicas y estrategias tratadas en este tutorial. Dominar estos conceptos puede mejorar significativamente tu capacidad de análisis financiero.

¿Qué es el interés compuesto?

El interés compuesto representa el crecimiento exponencial del dinero a lo largo del tiempo. A diferencia del interés simple, que crece linealmente, el interés compuesto se acelera a medida que los intereses devengados en cada periodo pasan a formar parte del capital del periodo siguiente.

El poder del interés compuesto se hace evidente al visualizar las inversiones a largo plazo. Supongamos que una ligera diferencia en los tipos de interés (como un 6% frente a un 8%) puede dar lugar a resultados radicalmente distintos durante décadas, lo que podría significar la diferencia entre una jubilación cómoda y una lucha financiera.

La fórmula del interés compuesto

El interés compuesto se calcula mediante la fórmula

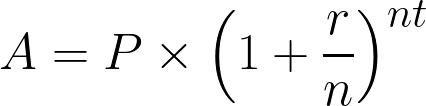
Fórmula del interés compuesto. Imagen del autor.

Dónde:

• A = Importe final después de intereses
• P = Principal (inversión inicial)
• r = Tipo de interés anual (en forma decimal)
• n = Número de veces que se capitalizan los intereses al año
• t = Número de años

Ahora que hemos comprendido el concepto y la fórmula matemática, vamos a aplicarla en Excel.

Cómo calcular el interés compuesto en Excel

Para aplicar esta fórmula en Excel, crea una estructura básica de hoja de cálculo con celdas claramente etiquetadas para cada variable.

Primero, organiza tu hoja de cálculo con las siguientes etiquetas:

• Celda A1: "Director"
• Celda A2: "Tipo de interés anual"
• Celda A3: "Períodos compuestos por año"
• Celda A4: "Tiempo (años)"
• Celda A5: "Importe final"

A continuación, introduce tus valores en la columna B:

• Celda B1: Introduce tu importe principal (por ejemplo, 1000)

• Celda B2: Introduce tu tipo de interés como decimal (por ejemplo, 0.05 para 5%)

• Celda B3: Introduce el número de periodos de capitalización al año (por ejemplo, 12 para mensual)

• Celda B4: Introduce el tiempo en años (por ejemplo, 5)

Después de configurar los datos, tu hoja de Excel debería tener el siguiente aspecto:

Configurar la tabla de Excel. Imagen del autor.

Por último, en la celda B5, introduce la fórmula del interés compuesto:

=B1*(1+B2/B3)^(B3*B4)

Fórmula de interés compuesto en Excel. Imagen del autor.

Esta fórmula aplica directamente la ecuación matemática anterior, calculando el importe final después del interés compuesto.

Cálculo del interés compuesto. Imagen del autor.

Utilizar la función FV()

Aunque la fórmula manual funciona bien, Excel proporciona funciones financieras incorporadas que simplifican el cálculo del interés compuesto. La función FV() (Valor Futuro) es especialmente útil para calcular el interés compuesto cuando se realizan pagos periódicos o inversiones.

La sintaxis de la función FV() es:

=FV(rate, nper, pmt, [pv], [type])

Dónde:

• rate = Tipo de interés por período

• nper = Número total de periodos de pago

• pmt = Pago realizado cada periodo (introduce 0 si no hay ninguno)

• pv = Valor actual (capital inicial), debe introducirse como número negativo

• type = Cuándo vencen los pagos (0 para final de periodo, 1 para principio)

Vamos a modificar nuestra hoja de cálculo para utilizar la función FV():

• Celda A6: "Uso de la función FV()"

Escribe lo siguiente en la celda B6:

=FV(B2/B3, B3*B4, 0, -B1)

Calcular el interés compuesto utilizando FV(). Imagen del autor.

Ten en cuenta que dividimos el tipo de interés anual por el número de periodos de capitalización para obtener el tipo por periodo, e introducimos el capital como un número negativo, tal y como exige la función.

Deberías poder ver el interés compuesto calculado como se indica a continuación:

Interés compuesto utilizando FV(). Imagen del autor.

Utilizar la función PMT()

La función PMT() calcula el pago de un préstamo basándose en pagos constantes y un tipo de interés constante. Aunque está diseñado principalmente para el pago de préstamos, puede adaptarse a situaciones de interés compuesto en las que quieras determinar cantidades de aportación periódicas para alcanzar una suma objetivo.

La sintaxis de la función PMT() es:

=PMT(rate, nper, pv, [fv], [type])

Dónde:

• rate = Tipo de interés por período

• nper = Número total de periodos de pago

• pv = Valor actual (capital inicial)

• fv = Valor futuro (la cantidad objetivo que quieres alcanzar)

• type = Cuándo vencen los pagos (0 para final de periodo, 1 para principio)

Añadámoslo a nuestra hoja de cálculo:

• Celda A7: "Importe objetivo"

• Célula B7: Introduce tu importe objetivo (por ejemplo, 5000)

• Celda A8: "Pago mensual requerido"

Escribe lo siguiente en la celda B8:

=PMT(B2/12, B4*12, -B1, B7)

del interés compuesto mediante PMT()Cálculo del interés compuesto mediante PMT(). Imagen del autor.

Esta fórmula calcula cuánto tienes que aportar mensualmente para alcanzar tu importe objetivo, teniendo en cuenta tu capital inicial y el tipo de interés.

La cuota mensual calculada puede verse como sigue:

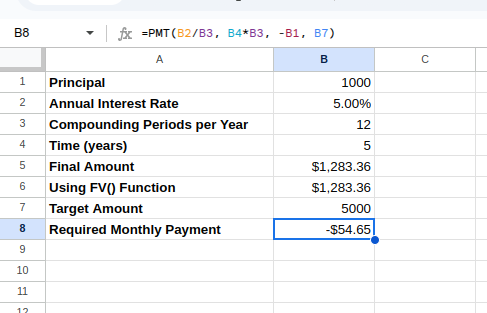
Interés compuesto utilizando PMT(). Imagen del autor.

La función PMT() de Excel devuelve por defecto un valor negativo porque está diseñada desde la perspectiva del flujo de caja:

• Los valores negativos representan dinero que pagas (salida de efectivo)
• Los valores positivos representan el dinero que recibes (entrada de efectivo)

El interés compuesto de Excel en acción

La fórmula del interés compuesto en Excel tiene numerosas aplicaciones en el mundo real en contextos de finanzas personales y empresariales. Exploremos algunos de estos supuestos prácticos.

Ahorros e inversiones

Una de las aplicaciones más habituales del cálculo del interés compuesto es proyectar el crecimiento de las cuentas de ahorro o inversión. Comprender cómo crece el dinero con el tiempo puede ayudarnos a tomar decisiones con conocimiento de causa.

Vamos a crear un modelo de proyección de ahorro para la jubilación en una nueva sección de nuestra hoja de cálculo. Tras introducir "Proyección de ahorro para la jubilación" en la celda D1, puedes configurar tus parámetros en las celdas D2 a D6:

• Célula D2: "Inversión inicial" con E2: 10000

• Célula D3: "Contribución mensual" con E3: 500

• Celda D4: "Tipo de interés anual" con E4: 0.07

• Celda D5: "Horizonte temporal (años)" con E5: 30

• Celda D6: "Frecuencia de Compuesto" con E6: "Mensual"

Tras introducir "Valor Futuro Proyectado" en la celda D7, escribe la siguiente ecuación en E7:

=FV(E4/12, E5*12, -E3, -E2)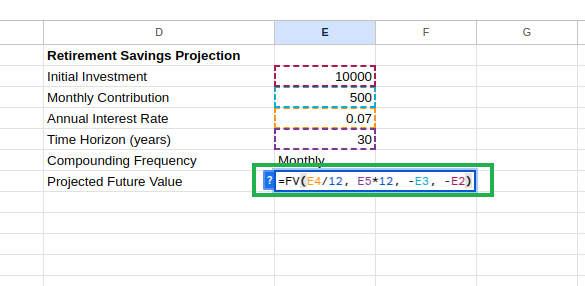

Cálculo del valor futuro proyectado. Imagen del autor.

Esta fórmula proyecta tus ahorros para la jubilación, teniendo en cuenta tanto tu inversión inicial como las aportaciones periódicas. Puedes ver el valor futuro como se indica a continuación:

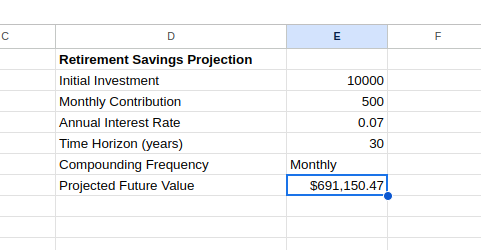
Valor futuro proyectado utilizando FV(). Imagen del autor.

Podemos mejorar este modelo creando una tabla de proyección año por año:

• En la celda D9, introduce "Proyección anual".

• En la celda D10, introduce "Año" y en la celda E10, introduce "Saldo".

• En la celda D11, introduce 0 (año de inicio)

• En la celda E11, introduce tu inversión inicial: =E2

• En la celda D12, introduce 1

• En la celda E12, calcula el saldo después del año 1:

=FV($E$4/12, 1*12, -$E$3, -E11)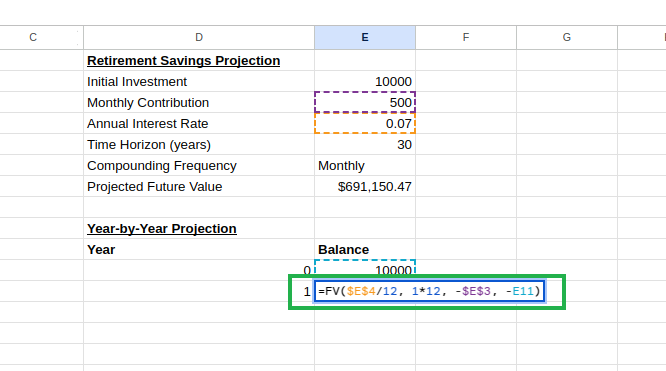

Crear una tabla de proyección año por Crear una tabla de proyección año por año. Imagen del autor.

• Selecciona las celdas D11 y D12, luego haz clic y arrastra el tirador de relleno (pequeño cuadrado en la esquina inferior derecha) hasta la fila 41 para crear los años 0 a 30
• Selecciona la celda E12, luego haz clic y arrastra el tirador de relleno hasta la fila 41

Excel ajustará automáticamente las referencias de las celdas de cada fila, creando una secuencia de cálculos en la que cada año se basa en el saldo del año anterior.

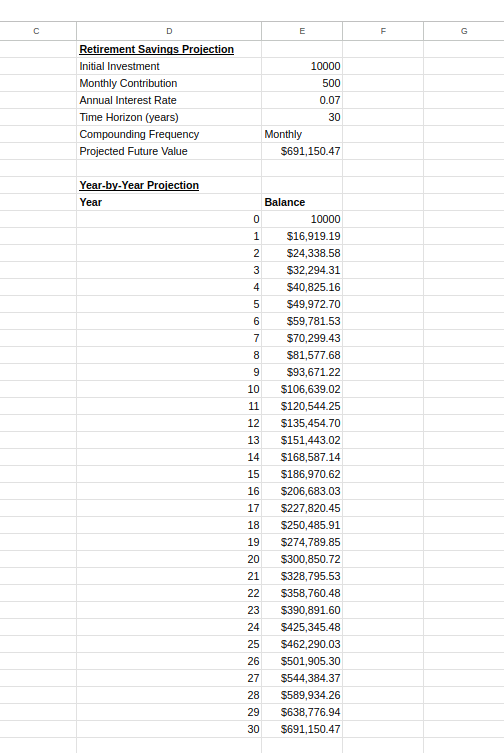
Tabla de proyección año por año. Imagen del autor.

Este gráfico puede ayudarte a comprender cómo crecen tus ahorros a lo largo del tiempo y puede motivar la inversión constante al ilustrar el patrón de crecimiento acelerado típico del interés compuesto.

Cálculo de préstamos

El interés compuesto también se aplica a los préstamos, en los que el interés se acumula sobre el saldo restante. Las funciones de Excel pueden ayudarte a comprender diversos aspectos de los préstamos, desde los pagos mensuales hasta el total de intereses pagados.

Para crear un plan de amortización de préstamo, configura los parámetros de tu préstamo como se muestra a continuación:

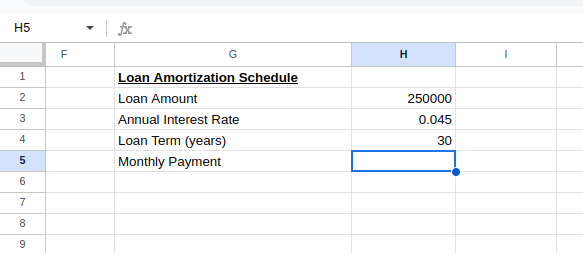Cálculo de la cuota mensual del préstamoCálculo de la cuota mensual del préstamo. Imagen del autor.

En la celda H3, escribe lo siguiente para calcular el pago mensual:

=PMT(H3/12, H4*12, H2)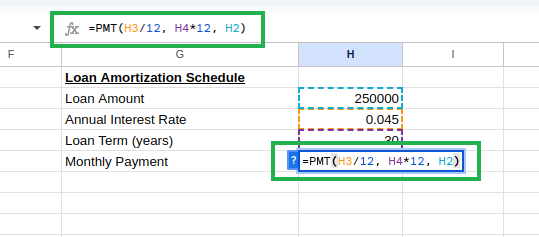

Cálculo de la cuota mensual del préstamo mediante PMT()Cálculo de la cuota mensual del préstamo mediante PMT(). Imagen del autor.

Verías el pago mensual como

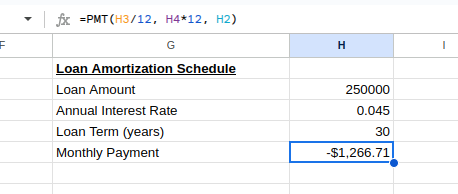
Cuota mensual del préstamo. Imagen del autor.

A continuación, configura la tabla del plan de amortización con una cabecera como la que aparece a continuación:

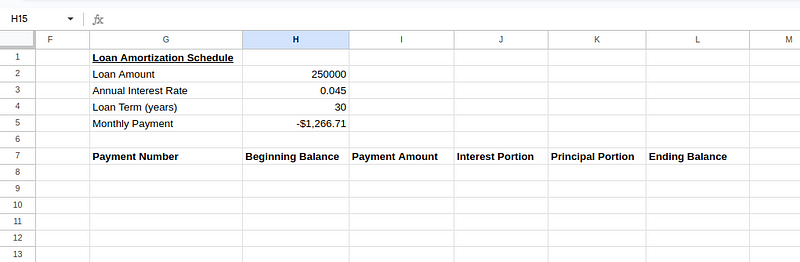Crear tabla de plan de amortizaciónCrear tabla de plan de amortización. Imagen del autor.

Introduce los valores iniciales del primer pago (fila 8):

• Móvil G8: 1 (primer pago)

• Celda H8: =H2 (importe inicial del préstamo)

• Celda I8: =ABS(H5) (importe del pago, utilizando ABS() para convertir el resultado negativo de PMT() en positivo)

• Celda J8: =H8*($H$3/12) (parte de intereses: saldo inicial × tipo mensual)

• Celda K8: =I8-J8 (parte del principal: importe del pago - parte de los intereses)

• Celda L8: =H8-K8 (saldo final: saldo inicial - parte principal)

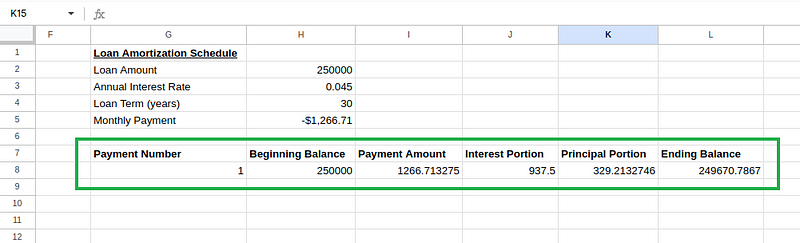Cálculos de tablas de amortización. Imagen del autor.

Para el segundo pago (fila 9), crea las siguientes fórmulas:

• Móvil G9: 2 (segundo pago)

• Celda H9: =L8 (el saldo inicial es igual al saldo final del pago anterior)

• Celda I9: =I8 (el importe del pago no varía)

• Celda J9: =H9*($H$3/12) (parte de intereses basada en el nuevo saldo inicial)

• Célula K9: =I9-J9 (parte principal)

• Celda L9: =H9-K9 (saldo final)

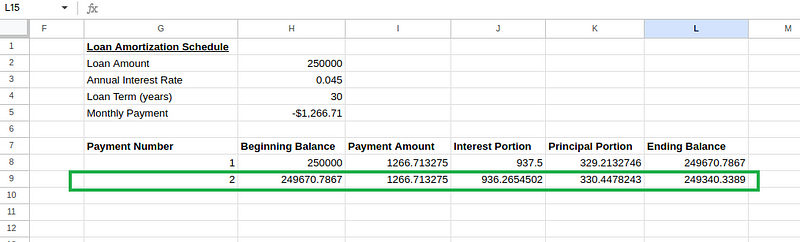Cálculos de la tabla de amortizaciónCálculos de la tabla de amortización. Imagen del autor.

A continuación, selecciona las celdas H9 a L9 y arrástralas hasta la fila 367 (para los 360 pagos).

En la celda H6, podemos calcular el total de intereses pagados: 

=SUM(J8:J367)

El horario final debería ser el siguiente

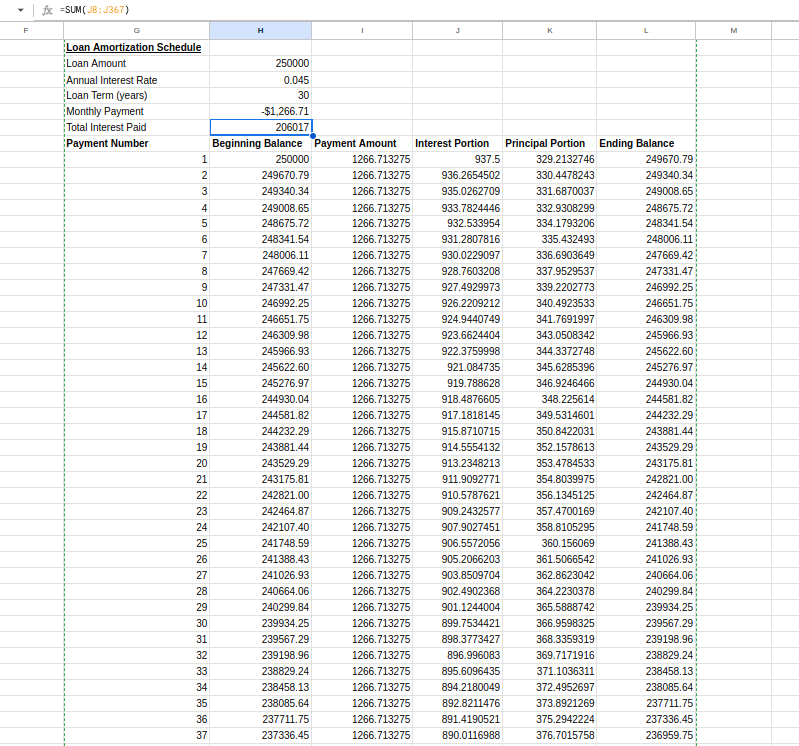Tabla del plan de amortizaciónTabla del plan de amortización. Imagen del autor.

Este plan de amortización revela cómo afecta cada pago al saldo de tu préstamo y a la importante cantidad de intereses pagados a lo largo de la vida del préstamo. Los pagos anticipados cubren principalmente los intereses, mientras que los pagos posteriores reducen sobre todo el capital: una idea importante para entender los préstamos hipotecarios.

Técnicas avanzadas de interés compuesto

Exploremos escenarios en los que se utilizan algunas técnicas avanzadas, como el manejo de periodos de capitalización irregulares y tipos de interés variables.

Tipos de interés variables

Los escenarios del mundo real suelen implicar tipos de interés variables, como las hipotecas de tipo variable o las inversiones vinculadas al mercado. Excel puede manejar estos escenarios complejos con alguna configuración adicional.

Podemos crear un modelo con distintos tipos de interés para distintos periodos de tiempo. Vamos a establecer una tabla de tipos de interés variable suponiendo que los tipos de interés van a aumentar un 0,5% cada 5 años:

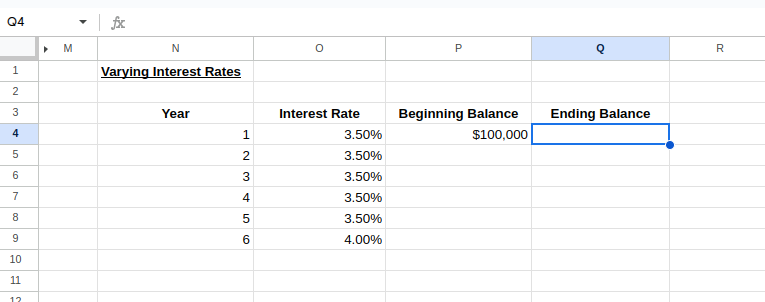Configurar una tabla para tipos de interés variables. Imagen del autor.

Para calcular el saldo final del Año 1 y el saldo inicial del Año 2, escribe lo siguiente:

• Célula Q4: =P4*(1+O4)

• Célula P5: =Q4

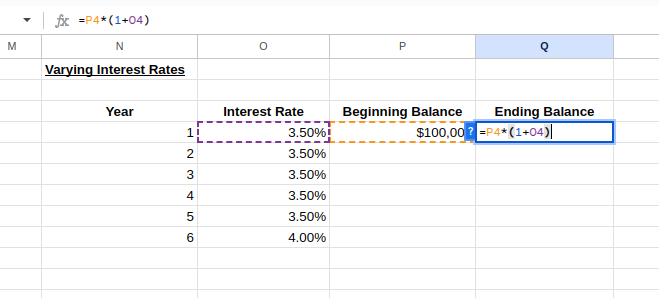Cálculos de tipos de interés variables. Imagen del autor.

Ahora podemos seleccionar las filas de Años 1-2 y arrastrar hacia abajo para ampliar la tabla hasta el número de años que deseemos, modificando los tipos de interés según sea necesario, como se muestra en la imagen siguiente:

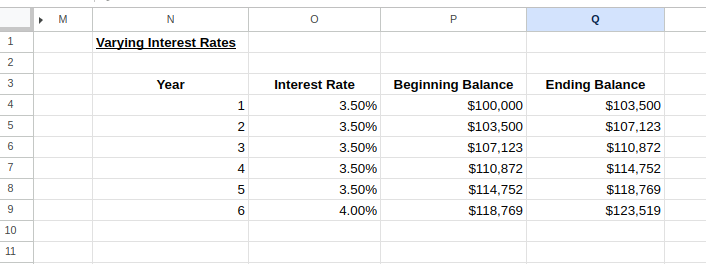Calculadora de tipos de interés variables. Imagen del autor.

Este modelo te permite visualizar cómo afectan los cambios en los tipos de interés a tu inversión o préstamo a lo largo del tiempo. 

Frecuencia de composición

Los productos financieros del mundo real suelen utilizar periodos de capitalización no estándar. Algunas inversiones se componen trimestralmente, otras mensualmente y algunas incluso diariamente. Estas diferencias en la frecuencia de capitalización pueden afectar significativamente a tus rendimientos a lo largo del tiempo.

Para acomodar estas variaciones en Excel, puedes ajustar la fórmula del interés compuesto en consecuencia. Supongamos que para calcular una inversión de 10.000 $ al 6% de interés anual con capitalización diaria durante 5 años se utilizara esta fórmula:

=10000*(1+0.06/365)^(365*5)

Un ejemplo de calculadora de capitalización irregular tendrá el siguiente aspecto:

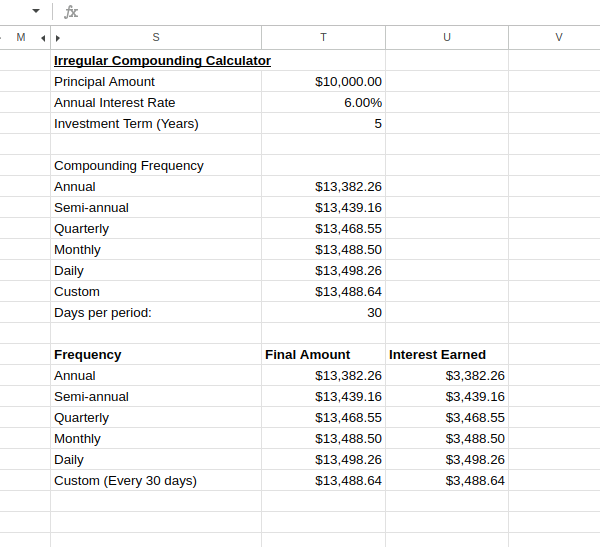Calculadora de capitalización irregular. Imagen del autor.

Esta comparación demuestra claramente cómo afecta la frecuencia compuesta a los rendimientos de tu inversión.

Como puedes ver, la capitalización más frecuente produce mayores rendimientos, aunque el beneficio incremental disminuye a medida que aumenta la frecuencia. Este conocimiento es especialmente valioso a la hora de evaluar productos financieros que anuncian diferentes métodos de capitalización.

Conclusión

A lo largo de esta guía, hemos explorado diversas aplicaciones prácticas de las fórmulas de interés compuesto de Excel. Desde la comprensión de la fórmula matemática fundamental hasta la aplicación de las funciones financieras de Excel como FV() y PMT(), ahora disponemos de las herramientas esenciales para realizar cálculos financieros significativos.

Para profundizar tus conocimientos de Excel más allá de este tutorial, considera la posibilidad de inscribirte en nuestro curso de Modelización financiera en Excel en Excel. Este curso se basa en los conceptos fundamentales tratados en el tutorial con técnicas avanzadas de modelización financiera.