PyTorch Tutorial: Ein einfaches neuronales Netz von Grund auf aufbauen

In diesem PyTorch-Tutorial werden wir die Kernfunktionen neuronaler Netze kennenlernen und unsere eigenen Netze von Grund auf neu aufbauen. Das Hauptziel dieses Artikels ist es, die Grundlagen von PyTorch, einer optimierten Deep-Learning-Tensor-Bibliothek, zu demonstrieren und dir gleichzeitig einen detaillierten Einblick in die Funktionsweise neuronaler Netze zu geben. 

Hinweis: Schau dir den DataCamp-Arbeitsbereich an, um den Code in diesem Artikel nachzuvollziehen.

Was sind neuronale Netze? 

Neuronale Netze werden auch künstliche neuronale Netze (ANNs) genannt. Diese Architektur bildet die Grundlage für Deep Learning, eine Untergruppe des maschinellen Lernens, die sich mit Algorithmen beschäftigt, die sich an der Struktur und Funktion des menschlichen Gehirns orientieren.  Vereinfacht gesagt, bilden neuronale Netze die Grundlage für Architekturen, die nachahmen, wie biologische Neuronen sich gegenseitig Signale geben. 

Deshalb findest du oft Ressourcen, die die ersten fünf Minuten damit verbringen, die neuronale Struktur des menschlichen Gehirns darzustellen, um dir zu zeigen, wie ein neuronales Netzwerk visuell funktioniert. Wenn du aber keine fünf Minuten mehr Zeit hast, ist es einfacher, ein neuronales Netzwerk als eine Funktion zu definieren, die Eingaben auf gewünschte Ausgaben abbildet. 

Die generische Architektur des neuronalen Netzes besteht aus folgenden Elementen:

• Eingabeschicht: Die Daten werden über die Eingabeschicht in das Netz eingespeist. Die Anzahl der Neuronen in der Eingabeschicht entspricht der Anzahl der Merkmale in den Daten. Die Eingabeschicht wird technisch gesehen nicht zu den Schichten des Netzes gezählt, da an dieser Stelle keine Berechnungen stattfinden. 
• Verdeckte Schicht: Die Schichten zwischen der Eingabe- und der Ausgabeschicht werden als versteckte Schichten bezeichnet. Ein Netz kann eine beliebige Anzahl von versteckten Schichten haben - je mehr versteckte Schichten es gibt, desto komplexer ist das Netz. 
• Ausgangsschicht: Die Ausgabeschicht wird verwendet, um eine Vorhersage zu treffen. 
• Neuronen: Jede Schicht besteht aus einer Sammlung von Neuronen, die mit Neuronen in anderen Schichten interagieren. 
• Aktivierungsfunktion: Führt nicht-lineare Transformationen durch, damit das Modell komplexe Muster aus den Daten lernen kann. 

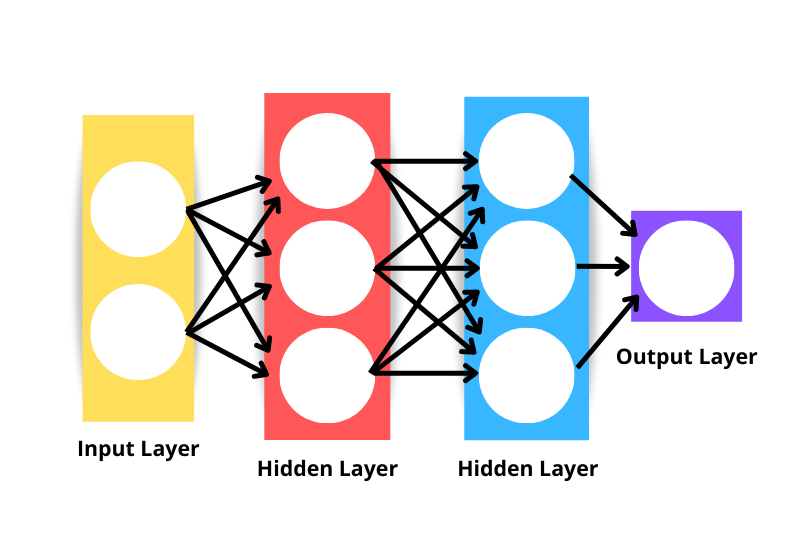
Beachte, dass das neuronale Netzwerk in der obigen Abbildung als dreischichtiges neuronales Netzwerk angesehen wird und nicht als vierschichtiges - das liegt daran, dass wir die Eingabeschicht nicht als Schicht zählen. Die Anzahl der Schichten in einem Netz ist also die Anzahl der versteckten Schichten plus der Ausgabeschicht.

Wie funktionieren neuronale Netze? 

Zerlegen wir den Algorithmus in kleinere Komponenten, um besser zu verstehen, wie neuronale Netze funktionieren.

Gewicht Initialisierung

Die Initialisierung der Gewichte ist die erste Komponente in der Architektur des neuronalen Netzes. Die anfänglichen Gewichte legen wir fest, um den Startpunkt für den Optimierungsprozess des neuronalen Netzmodells zu definieren. 

Wie wir unsere Gewichte setzen, ist wichtig, vor allem wenn wir tiefe Netze aufbauen. Das liegt daran, dass tiefe Netze eher unter dem explodierenden oder verschwindenden Gradientenproblem leiden. Das verschwindende und das explodierende Gradientenproblem sind zwei Konzepte, die über den Rahmen dieses Artikels hinausgehen, aber beide beschreiben ein Szenario, in dem der Algorithmus nicht lernen kann. 

Auch wenn die Gewichtsinitialisierung das Problem des verschwindenden oder explodierenden Gradienten nicht vollständig löst, so trägt sie doch dazu bei, es zu verhindern. 

Hier sind ein paar gängige Ansätze für die Gewichtsinitialisierung: 

Null-Initialisierung

Null-Initialisierung bedeutet, dass die Gewichte mit Null initialisiert werden. Das ist keine gute Lösung, denn unser neuronales Netz würde die Symmetrie nicht brechen - es würde nicht lernen. 

Wenn die Gewichte eines neuronalen Netzes mit einem konstanten Wert initialisiert werden, können wir davon ausgehen, dass es schlecht abschneidet, da alle Schichten das Gleiche lernen. Wenn alle Ausgänge der versteckten Einheiten denselben Einfluss auf die Kosten haben, sind die Gradienten identisch. 

Zufällige Initialisierung

Die zufällige Initialisierung bricht die Symmetrie, was bedeutet, dass sie besser ist als eine Null-Initialisierung, aber einige Faktoren können die Gesamtqualität des Modells bestimmen. 

Wenn die Gewichte zum Beispiel zufällig mit großen Werten initialisiert werden, können wir davon ausgehen, dass jede Matrixmultiplikation zu einem deutlich größeren Wert führt. Wenn in solchen Szenarien eine Sigmoid-Aktivierungsfunktion angewendet wird, ist das Ergebnis ein Wert nahe eins, was die Lernrate verlangsamt.

Ein weiteres Szenario, in dem die zufällige Initialisierung zu Problemen führen kann, ist, wenn die Gewichte zufällig auf kleine Werte initialisiert werden. In diesem Fall ergibt jede Matrixmultiplikation deutlich kleinere Werte, und die Anwendung einer Sigmoidfunktion ergibt einen Wert, der näher bei Null liegt, was die Lerngeschwindigkeit ebenfalls verlangsamt. 

Xavier/Glorot-Initialisierung 

Die Xavier- oder Glorot-Initialisierung - beide Namen sind gebräuchlich - ist ein heuristischer Ansatz zur Initialisierung von Gewichten. Dieser Initialisierungsansatz ist üblich, wenn eine tanh- oder sigmoide Aktivierungsfunktion auf den gewichteten Durchschnitt angewendet wird. Der Ansatz wurde erstmals 2010 in einer Forschungsarbeit mit dem Titel Understanding the difficulty of training deep feedforward neural networks von Xavier Glorot und Yoshua Bengio vorgeschlagen. Diese Initialisierungstechnik zielt darauf ab, die Varianz im gesamten Netzwerk gleich zu halten, damit die Gradienten nicht explodieren oder verschwinden. 

He/Kaiming Initialisierung 

Die He- oder Kaiming-Initialisierung ist ein weiterer heuristischer Ansatz. Der Unterschied zur He- und Xavier-Heuristik besteht darin, dass die He-Initialisierung einen anderen Skalierungsfaktor für die Gewichte verwendet, der die Nichtlinearität der Aktivierungsfunktionen berücksichtigt. 

Wenn also die ReLU-Aktivierungsfunktion in den Schichten verwendet wird, ist die He-Initialisierung der empfohlene Ansatz. Mehr über diesen Ansatz erfährst du unter Vertiefung von Gleichrichtern: Übertreffen der menschlichen Leistung bei der ImageNet-Klassifizierung von He et al.

Vorwärtsausbreitung

Neuronale Netze funktionieren, indem sie einen gewichteten Durchschnitt plus einen Bias-Term bilden und eine Aktivierungsfunktion anwenden, um eine nichtlineare Transformation hinzuzufügen. Beim gewichteten Durchschnitt bestimmt jedes Gewicht die Wichtigkeit jedes Merkmals (d.h. wie viel es zur Vorhersage des Ergebnisses beiträgt).

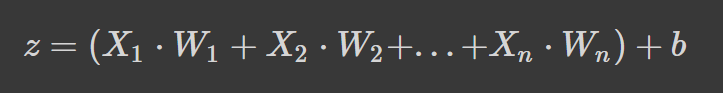
Die obige Formel ist der gewogene Durchschnitt plus ein Verzerrungsterm, wobei, 

• z ist die gewichtete Summe der Eingaben eines Neurons
• Wn bezeichnet die Gewichte
• Xn steht für die unabhängigen Variablen und
• b ist der Bias-Term.

Wenn dir die Formel bekannt vorkommt, liegt das daran, dass es sich um eine lineare Regression handelt. Ohne die Einführung von Nichtlinearität in die Neuronen hätten wir eine lineare Regression, die ein einfaches Modell ist. Die nicht-lineare Transformation ermöglicht es unserem neuronalen Netz, komplexe Muster zu lernen. 

Aktivierungsfunktionen

Wir haben bereits im Abschnitt über die Initialisierung der Gewichte auf einige Aktivierungsfunktionen angespielt, aber jetzt weißt du, wie wichtig sie in einer neuronalen Netzwerkarchitektur sind.

Wir wollen uns einige gängige Aktivierungsfunktionen genauer ansehen, die du wahrscheinlich siehst, wenn du Forschungsarbeiten und den Code anderer Leute liest.  

Sigmoid

Die Sigmoidfunktion ist durch eine S-förmige Kurve gekennzeichnet, die zwischen den Werten Null und Eins begrenzt ist. Sie ist eine differenzierbare Funktion, d.h. die Steigung der Kurve kann an zwei beliebigen Punkten gefunden werden, und sie ist monoton, d.h. sie ist weder vollständig steigend noch fallend. Für binäre Klassifizierungsprobleme würdest du normalerweise die Sigmoid-Aktivierungsfunktion verwenden.

Hier erfährst du, wie du deine eigene Sigmoid-Funktion mit Python visualisieren kannst: 

# Sigmoid function in Python
import matplotlib.pyplot as plt
import numpy as np

x = np.linspace(-5, 5, 50)
z = 1/(1 + np.exp(-x))

plt.subplots(figsize=(8, 5))
plt.plot(x, z)
plt.grid()
plt.show()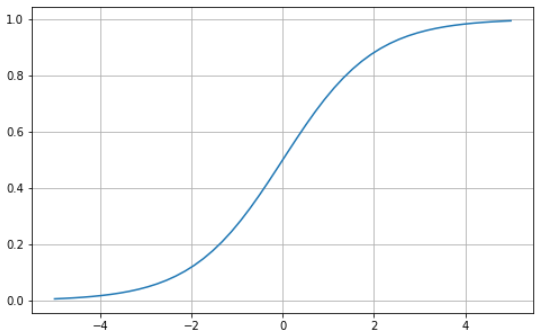

Tanh

Der hyperbolische Tangens (tanh) hat die gleiche "S"-förmige Kurve wie die Sigmoidfunktion, nur dass die Werte zwischen -1 und 1 begrenzt sind. So werden kleine Eingaben näher an -1 und größere Eingaben näher an 1 abgebildet.

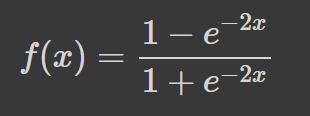
Hier ist ein Beispiel für eine tanh-Funktion, die mit Python visualisiert wird: 

# tanh function in Python
import matplotlib.pyplot as plt
import numpy as np

x = np.linspace(-5, 5, 50)
z = np.tanh(x)

plt.subplots(figsize=(8, 5))
plt.plot(x, z)
plt.grid()
plt.show()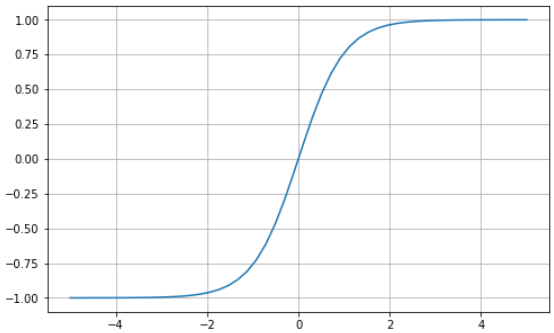

Softmax

Die Softmax-Funktion wird in der Regel als Aktivierungsfunktion in der Ausgabeschicht verwendet. Es ist eine Verallgemeinerung der Sigmoidfunktion auf mehrere Dimensionen. Daher wird es in neuronalen Netzen verwendet, um die Klassenzugehörigkeit bei mehr als zwei Labels vorherzusagen. 

Rektifizierte Lineareinheit (ReLU)

Die Verwendung der Sigmoid- oder Tanh-Funktion zum Aufbau tiefer neuronaler Netze ist riskant, da sie eher unter dem Problem des verschwindenden Gradienten leiden. Die Aktivierungsfunktion ReLU (rectified linear unit) wurde als Lösung für dieses Problem entwickelt und ist häufig die Standardaktivierungsfunktion für verschiedene neuronale Netze. 

Hier ist ein visuelles Beispiel für die ReLU-Funktion in Python: 

# ReLU in Python
import matplotlib.pyplot as plt
import numpy as np

x = np.linspace(-5, 5, 50)
z = [max(0, i) for i in x]

plt.subplots(figsize=(8, 5))
plt.plot(x, z)
plt.grid()
plt.show()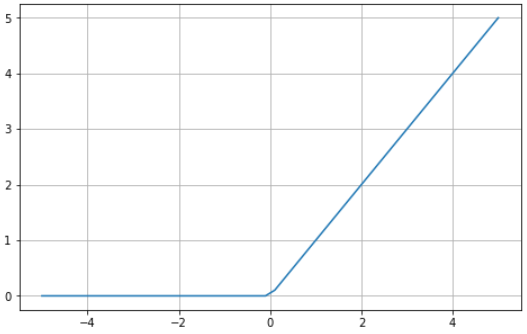

ReLU ist zwischen Null und Unendlich begrenzt: Beachte, dass die Funktion bei Eingabewerten kleiner oder gleich Null Null zurückgibt und bei Werten über Null den angegebenen Eingabewert zurückgibt (d.h. wenn du zwei eingibst, wird zwei zurückgegeben). Letztendlich verhält sich die ReLU-Funktion sehr ähnlich wie eine lineare Funktion, wodurch sie viel einfacher zu optimieren und umzusetzen ist. 

Der Prozess von der Eingabe- zur Ausgabeschicht wird als Forward Pass oder Forward Propagation bezeichnet. In dieser Phase werden die vom Modell erzeugten Ausgaben zur Berechnung einer Kostenfunktion verwendet, um zu ermitteln, wie das neuronale Netz nach jeder Iteration abschneidet. Diese Informationen werden dann an das Modell zurückgegeben, um die Gewichte zu korrigieren, so dass das Modell bessere Vorhersagen machen kann - ein Prozess, der als Backpropagation bekannt ist. 

Backpropagation

Am Ende des ersten Vorwärtsdurchgangs macht das Netz Vorhersagen mit den initialisierten Gewichten, die nicht angepasst werden. Es ist also sehr wahrscheinlich, dass die Vorhersagen des Modells nicht zutreffen werden. Mit Hilfe des Verlustes, der durch die Vorwärtspropagation berechnet wurde, leiten wir Informationen zurück durch das Netzwerk, um die Gewichte in einem Prozess, der als Backpropagation bekannt ist, fein abzustimmen. 

Letztlich nutzen wir die Optimierungsfunktion, um die Gewichte zu ermitteln, die die Fehlerquote reduzieren, das Modell zuverlässiger machen und seine Fähigkeit zur Generalisierung auf neue Fälle erhöhen. Wie das mathematisch funktioniert, würde den Rahmen dieses Artikels sprengen, aber interessierte Leser/innen können in unserem Kurs Einführung in Deep Learning in Python mehr über Backpropagation erfahren.

PyTorch Tutorial: Eine Schritt-für-Schritt-Anleitung zum Aufbau eines neuronalen Netzwerks von Grund auf

In diesem Artikel werden wir ein einfaches künstliches neuronales Netzwerkmodell mit der PyTorch-Bibliothek erstellen. Schau dir diesen DataCamp-Arbeitsbereich an, um dem Code zu folgen

PyTorch ist eine der beliebtesten Bibliotheken für Deep Learning. Es bietet ein viel direkteres Debugging-Erlebnis als TensorFlow. Es hat noch weitere Vorteile wie verteilte Schulungen, ein robustes Ökosystem, Cloud-Unterstützung, die Möglichkeit, produktionsreifen Code zu schreiben, usw. Mehr über PyTorch erfährst du im Lernpfad Einführung in Deep Learning mit PyTorch. 

Los geht's mit dem Lernprogramm. 

Datendefinition und -aufbereitung 

Der Datensatz, den wir in unserem Tutorial verwenden, ist make_circles von scikit-learn - siehe die Dokumentation. Es ist ein Spielzeugdatensatz, der einen großen Kreis mit einem kleineren Kreis in einer zweidimensionalen Ebene und zwei Merkmale enthält. Für unsere Demonstration haben wir 10.000 Stichproben verwendet und den Daten eine Standardabweichung von 0,05 Gaußschen Rauschen hinzugefügt. 

Bevor wir unser neuronales Netzwerk aufbauen, sollten wir unsere Daten in Trainings- und Testdatensätze aufteilen, damit wir die Leistung des Modells bei ungesehenen Daten bewerten können.

import matplotlib.pyplot as plt
from sklearn.datasets import make_circles
from sklearn.model_selection import train_test_split

# Create a dataset with 10,000 samples.
X, y = make_circles(n_samples = 10000,
                    noise= 0.05,
                    random_state=26)

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=.33, random_state=26)

# Visualize the data.
fig, (train_ax, test_ax) = plt.subplots(ncols=2, sharex=True, sharey=True, figsize=(10, 5))
train_ax.scatter(X_train[:, 0], X_train[:, 1], c=y_train, cmap=plt.cm.Spectral)
train_ax.set_title("Training Data")
train_ax.set_xlabel("Feature #0")
train_ax.set_ylabel("Feature #1")

test_ax.scatter(X_test[:, 0], X_test[:, 1], c=y_test)
test_ax.set_xlabel("Feature #0")
test_ax.set_title("Testing data")
plt.show()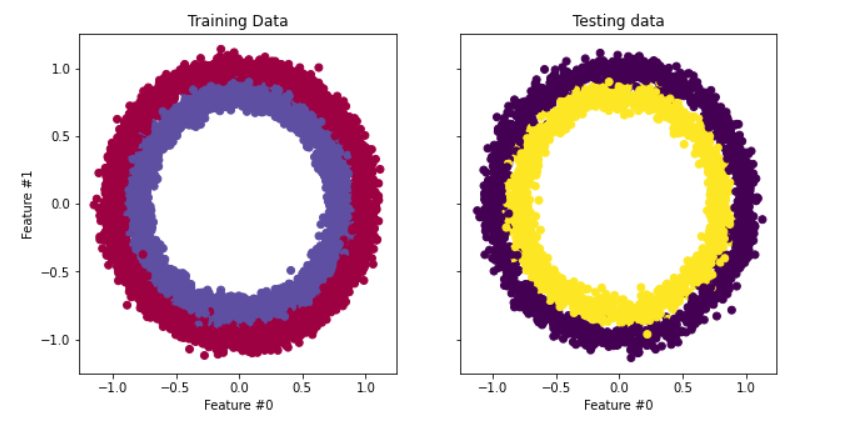

Der nächste Schritt ist die Umwandlung der Trainings- und Testdaten von NumPy-Arrays in PyTorch-Tensoren. Dazu erstellen wir einen eigenen Datensatz für unsere Trainings- und Testdateien. Wir werden auch das Dataloader-Modul von PyTorch nutzen, damit wir unsere Daten in Stapeln trainieren können. Hier ist der Code: 

import warnings
warnings.filterwarnings("ignore")

!pip install torch -q

import torch
import numpy as np
from torch.utils.data import Dataset, DataLoader

# Convert data to torch tensors
class Data(Dataset):
    def __init__(self, X, y):
        self.X = torch.from_numpy(X.astype(np.float32))
        self.y = torch.from_numpy(y.astype(np.float32))
        self.len = self.X.shape[0]
       
    def __getitem__(self, index):
        return self.X[index], self.y[index]
   
    def __len__(self):
        return self.len
   
batch_size = 64

# Instantiate training and test data
train_data = Data(X_train, y_train)
train_dataloader = DataLoader(dataset=train_data, batch_size=batch_size, shuffle=True)

test_data = Data(X_test, y_test)
test_dataloader = DataLoader(dataset=test_data, batch_size=batch_size, shuffle=True)

# Check it's working
for batch, (X, y) in enumerate(train_dataloader):
    print(f"Batch: {batch+1}")
    print(f"X shape: {X.shape}")
    print(f"y shape: {y.shape}")
    break


"""
Batch: 1
X shape: torch.Size([64, 2])
y shape: torch.Size([64])
"""

Nun wollen wir unser neuronales Netz implementieren und trainieren. 

Implementierung eines neuronalen Netzwerks & Modelltraining

Wir werden ein einfaches zweischichtiges neuronales Netz implementieren, das die Aktivierungsfunktion ReLU (torch.nn.functional.relu) verwendet. Dazu erstellen wir eine Klasse namens NeuralNetwork, die von nn.Module erbt. nn.Module ist die Basisklasse für alle in PyTorch erstellten neuronalen Netzwerkmodule. 

Hier ist der Code: 

import torch
from torch import nn
from torch import optim

input_dim = 2
hidden_dim = 10
output_dim = 1

class NeuralNetwork(nn.Module):
    def __init__(self, input_dim, hidden_dim, output_dim):
        super(NeuralNetwork, self).__init__()
        self.layer_1 = nn.Linear(input_dim, hidden_dim)
        nn.init.kaiming_uniform_(self.layer_1.weight, nonlinearity="relu")
        self.layer_2 = nn.Linear(hidden_dim, output_dim)
       
    def forward(self, x):
        x = torch.nn.functional.relu(self.layer_1(x))
        x = torch.nn.functional.sigmoid(self.layer_2(x))

        return x
       
model = NeuralNetwork(input_dim, hidden_dim, output_dim)
print(model)


"""
NeuralNetwork(
  (layer_1): Linear(in_features=2, out_features=10, bias=True)
  (layer_2): Linear(in_features=10, out_features=1, bias=True)
)
"""

Und das ist alles. 

Um das Modell zu trainieren, müssen wir eine Verlustfunktion für die Berechnung der Gradienten und einen Optimierer für die Aktualisierung der Parameter definieren. Für unsere Demonstration werden wir die binäre Kreuzentropie und den stochastischen Gradientenabstieg mit einer Lernrate von 0,1 verwenden. 

learning_rate = 0.1

loss_fn = nn.BCELoss()

optimizer = torch.optim.SGD(model.parameters(), lr=lea

Lass uns unser Modell trainieren

num_epochs = 100
loss_values = []


for epoch in range(num_epochs):
    for X, y in train_dataloader:
        # zero the parameter gradients
        optimizer.zero_grad()
       
        # forward + backward + optimize
        pred = model(X)
        loss = loss_fn(pred, y.unsqueeze(-1))
        loss_values.append(loss.item())
        loss.backward()
        optimizer.step()

print("Training Complete")

"""
Training Complete
"""

Da wir die Lernpfade nachverfolgt haben, können wir den Verlust des Modells im Laufe der Zeit sichtbar machen. 

step = range(len(loss_values))

fig, ax = plt.subplots(figsize=(8,5))
plt.plot(step, np.array(loss_values))
plt.title("Step-wise Loss")
plt.xlabel("Epochs")
plt.ylabel("Loss")
plt.show()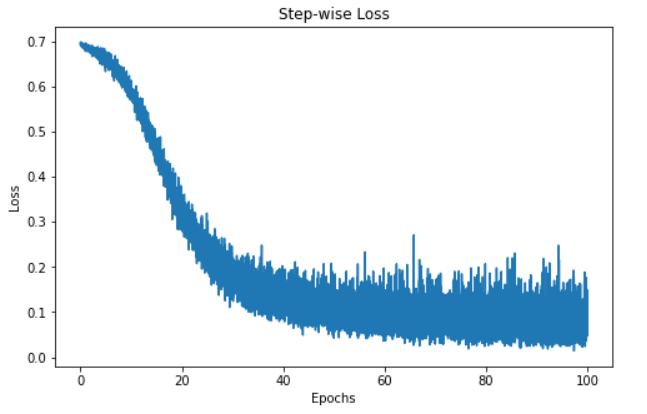

Die Visualisierung oben zeigt den Verlust unseres Modells über 100 Epochen. Zu Beginn liegt der Verlust bei 0,7 und nimmt dann allmählich ab - das zeigt uns, dass unser Modell seine Vorhersagen im Laufe der Zeit verbessert hat. Allerdings scheint das Modell um die 60-Epochen-Marke herum zu stagnieren, was verschiedene Gründe haben kann, z. B. dass sich das Modell in der Region eines lokalen oder globalen Minimums der Verlustfunktion befindet. 

Nichtsdestotrotz wurde das Modell trainiert und ist bereit, Vorhersagen für neue Fälle zu treffen - wie das geht, sehen wir uns im nächsten Abschnitt an.

Vorhersagen & Modellbewertung

Das Erstellen von Vorhersagen mit unserem neuronalen Netzwerk PyTorch ist ganz einfach. 

import itertools  # Import this at the top of your script

# Initialize required variables
y_pred = []
y_test = []
correct = 0
total = 0

"""
We're not training so we don't need to calculate the gradients for our outputs
"""
with torch.no_grad():
    for X, y in test_dataloader:
        outputs = model(X)  # Get model outputs
        predicted = np.where(outputs.numpy() < 0.5, 0, 1)  # Convert to NumPy and apply threshold
        predicted = list(itertools.chain(*predicted))  # Flatten predictions
        y_pred.append(predicted)  # Append predictions
        y_test.append(y.numpy())  # Append true labels as NumPy
        total += y.size(0)  # Increment total count
        correct += (predicted == y.numpy()).sum().item()  # Count correct predictions

print(f'Accuracy of the network on the 3300 test instances: {100 * correct // total}%')

"""
Accuracy of the network on the 3300 test instances: 97%
"""

Hinweis: Jeder Durchlauf des Codes würde eine andere Ausgabe erzeugen, sodass du möglicherweise nicht die gleichen Ergebnisse erhältst. 

Der obige Code durchläuft die Teststapel, die in der Variable test_dataloader gespeichert sind, ohne die Gradienten zu berechnen. Dann sagen wir die Instanzen im Stapel voraus und speichern die Ergebnisse in einer Variablen namens Outputs. Als Nächstes setzen wir alle Werte, die kleiner als 0,5 sind, auf 0 und alle, die gleich oder größer als 0,5 sind, auf 1. Diese Werte werden dann an eine Liste für unsere Vorhersagen angehängt.

Danach addieren wir die tatsächlichen Vorhersagen der Instanzen im Batch zu einer Variablen namens total. Dann berechnen wir die Anzahl der richtigen Vorhersagen, indem wir die Anzahl der Vorhersagen ermitteln, die den tatsächlichen Klassen entsprechen, und diese zusammenzählen. Die Gesamtzahl der korrekten Vorhersagen für jeden Stapel wird erhöht und in unserer Variable "korrekt" gespeichert.

Um die Genauigkeit des Gesamtmodells zu berechnen, multiplizieren wir die Anzahl der richtigen Vorhersagen mit 100 (um einen Prozentsatz zu erhalten) und teilen sie dann durch die Anzahl der Instanzen in unserem Testsatz. Unser Modell hatte eine Genauigkeit von 97%. Wir verwenden die Konfusionsmatrix und scikit-learns classification_report, um ein besseres Verständnis für die Leistung unseres Modells zu bekommen.

from sklearn.metrics import classification_report
from sklearn.metrics import confusion_matrix

import seaborn as sns

y_pred = list(itertools.chain(*y_pred))
y_test = list(itertools.chain(*y_test))

print(classification_report(y_test, y_pred))

"""
              precision    recall  f1-score   support

        0.0       0.98      0.97      0.98      1635
        1.0       0.98      0.98      0.98      1665

    accuracy                           0.98      3300
  macro avg       0.98      0.98      0.98      3300
weighted avg       0.98      0.98      0.98      3300

"""

cf_matrix = confusion_matrix(y_test, y_pred)

plt.subplots(figsize=(8, 5))

sns.heatmap(cf_matrix, annot=True, cbar=False, fmt="g")

plt.show()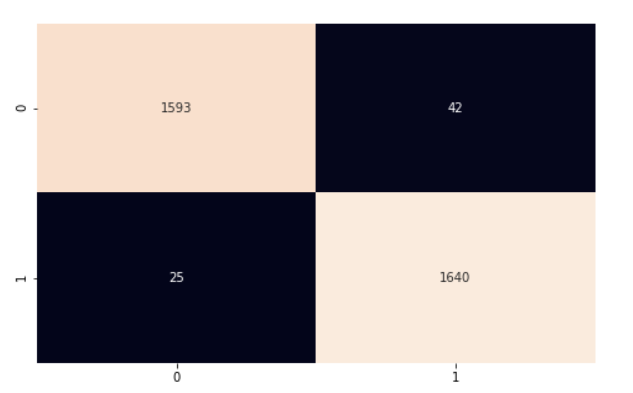

Unser Modell funktioniert ziemlich gut. Ich möchte dich ermutigen, den Code zu erforschen und einige Änderungen vorzunehmen, damit das, was wir in diesem Artikel behandelt haben, auch wirklich funktioniert.  

In diesem PyTorch-Tutorial haben wir die Grundlagen neuronaler Netze behandelt und PyTorch, eine Python-Bibliothek für Deep Learning, zur Implementierung unseres Netzwerks verwendet. Wir haben den Datensatz des Kreises aus scikit-learn verwendet, um ein zweischichtiges neuronales Netz für die Klassifizierung zu trainieren. Dann haben wir Vorhersagen für die Daten gemacht und unsere Ergebnisse anhand der Genauigkeitsmetrik bewertet.