Curso

Neste tutorial de PyTorch, vamos abordar as principais funções que alimentam as redes neurais e criar as nossas próprias redes do zero. O principal objetivo deste artigo é demonstrar os conceitos básicos de PyTorch, uma biblioteca de tensores de aprendido profundo otimizada, ao mesmo tempo em que apresenta a você um histórico detalhado de como funcionam as redes neurais.
Observação: confira este espaço de trabalho do DataCamp para acompanhar os códigos escritos neste artigo.
O que são redes neurais?
As redes neurais também são chamadas de redes neurais artificiais (ANNs, Artificial Neural Networks). A arquitetura forma a base do aprendizado profundo, que é apenas um subconjunto do aprendizado automático que trata de algoritmos inspirados na estrutura e no funcionamento do cérebro humano. Simplificando, as redes neurais formam a base de arquiteturas que imitam a forma como os neurônios biológicos transmitem sinais entre si.
Consequentemente, você encontrará com frequência recursos que passam os primeiros cinco minutos descrevendo a estrutura neural do cérebro humano para ajudá-lo a visualizar como funciona uma rede neural. Mas quando você não tem cinco minutos sobrando, é mais fácil definir uma rede neural como uma função que associa entradas a saídas desejadas.
A arquitetura genérica de uma rede neural consiste no seguinte:
- Camada de entrada: Os dados são inseridos na rede por meio da camada de entrada. O número de neurônios na camada de entrada é equivalente ao número de variáveis independentes nos dados. Tecnicamente, a camada de entrada não é considerada uma das camadas da rede porque não ocorre nenhum tipo de computação nesse ponto.
- Camada oculta: As camadas que ficam entre as camadas de entrada e saída são chamadas de camadas ocultas. Uma rede pode ter um número arbitrário de camadas ocultas. Quanto mais camadas ocultas houver, mais complexa será a rede.
- Camada de saída: A camada de saída é usada para fazer uma previsão.
- Neurônios: Cada camada tem um conjunto de neurônios que interagem com os neurônios de outras camadas.
- Função de ativação: Realiza transformações não lineares para ajudar o modelo a aprender padrões complexos a partir dos dados.
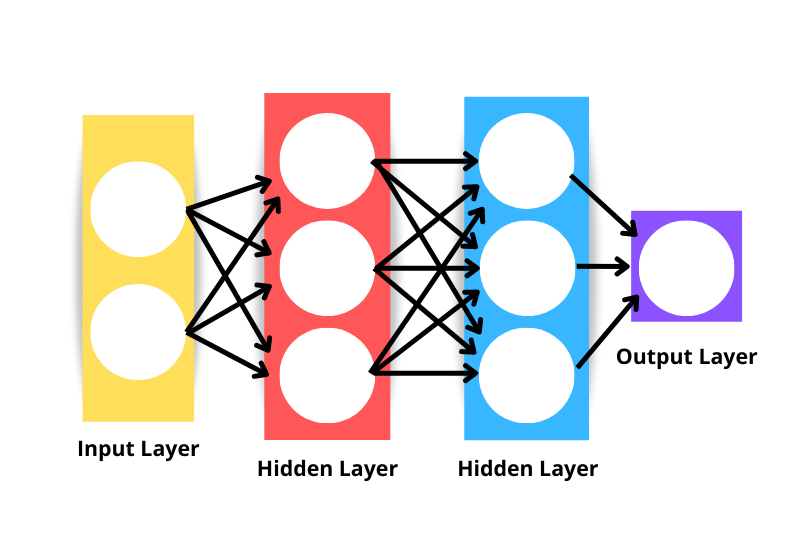
Observe que a rede neural exibida na imagem acima seria considerada uma rede neural de três camadas, e não de quatro – isso porque não a camada de entrada não foi considerada. Portanto, o número de camadas de uma rede é o número de camadas ocultas mais a camada de saída.
Como funcionam as redes neurais?
Vamos desmembrar o algoritmo em componentes menores para que você entenda melhor como funcionam as redes neurais.
Inicialização dos pesos
A inicialização dos pesos é o primeiro componente da arquitetura da rede neural. Os pesos iniciais que configuramos definem o ponto de partida do processo de otimização do modelo de rede neural.
A forma como definimos os pesos é importante, sobretudo ao criar redes profundas. Isso ocorre porque as redes profundas são mais propensas a sofrer com o problema de gradiente explosivo ou dissipação do gradiente. Os problemas de gradiente explosivo e dissipação do gradiente são dois conceitos que vão além do escopo deste artigo, mas ambos descrevem uma situação em que o algoritmo não consegue aprender.
Embora a inicialização dos pesos não resolva completamente o problema do gradiente explosivo ou da dissipação do gradiente, certamente contribui para sua prevenção.
Aqui vão algumas abordagens comuns de inicialização dos pesos:
Inicialização zero
A inicialização zero significa que os pesos são inicializados como zero. Não é uma boa solução, pois a rede neural não conseguiria quebrar a simetria – ela não aprenderia.
Sempre que um valor constante é usado para inicializar os pesos de uma rede neural, podemos esperar que ela tenha um desempenho ruim, pois todas as camadas aprenderão a mesma coisa. Se todas as saídas das unidades ocultas tiverem a mesma influência sobre o custo, então os gradientes serão idênticos.
Inicialização aleatória
A inicialização aleatória quebra a simetria, o que significa que é melhor do que a inicialização zero, mas alguns fatores podem ditar a qualidade geral do modelo.
Por exemplo: se os pesos forem inicializados aleatoriamente com valores altos, podemos esperar que cada multiplicação de matrizes resulte em um valor significativamente maior. Quando uma função de ativação sigmoide é aplicada nessas situações, o resultado é um valor próximo a um, o que diminui a taxa de aprendizado.
Outra situação em que a inicialização aleatória pode causar problemas é quando os pesos são inicializados aleatoriamente com valores pequenos. Nesse caso, cada multiplicação de matrizes gera valores significativamente menores, e a aplicação de uma função sigmoide produz um valor mais próximo de zero, o que também diminui a taxa de aprendizado.
Inicialização de Xavier/Glorot
Uma inicialização de Xavier, também conhecida como inicialização de Glorot, é uma abordagem heurística usada para inicializar pesos. É comum ver essa abordagem de inicialização sempre que uma função de ativação tanh ou sigmoide é aplicada à média ponderada. A abordagem foi proposta pela primeira vez em 2010, em um artigo de pesquisa intitulado Understanding the difficulty of training deep feedforward neural networks (Entendendo a dificuldade de treinar redes neurais profundas feedforward), de Xavier Glorot e Yoshua Bengio. Essa técnica de inicialização visa manter a variância igual em toda a rede para evitar que os gradientes explodam ou desapareçam.
Inicialização de He/Kaiming
A inicialização de He ou Kaiming é outra abordagem heurística. A diferença entre as heurísticas de He e de Xavier é que a inicialização de He usa um fator de escala diferente para os pesos considerando a não linearidade das funções de ativação.
Assim, quando a função de ativação ReLU é usada nas camadas, a inicialização de He é a abordagem recomendada. Para saber mais sobre essa abordagem, acesse . Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification, de He et al.
Propagação direta
As redes neurais funcionam calculando uma média ponderada mais um termo de viés (bias) e aplicam uma função de ativação para adicionar uma transformação não linear. Na formulação da média ponderada, cada peso determina a importância de cada variável independente ou feature (ou seja, o quanto ela contribui para prever o resultado).
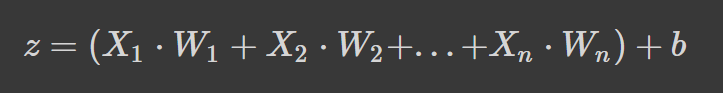
A fórmula acima é a média ponderada somada a um termo de viés, onde
- z é a soma ponderada da entrada de um neurônio
- Wn denota os pesos
- Xn denota as variáveis independentes e
- b é o termo de viés.
Se a fórmula lhe parece familiar, é porque se trata de um regressão linear. Sem introduzir a não linearidade nos neurônios, teríamos uma regressão linear, que é um modelo simples. A transformação não linear permite que a rede neural aprenda padrões complexos.
Funções de ativação
Já fizemos alusão a algumas funções de ativação na seção de inicialização de pesos, mas agora você sabe a importância delas na arquitetura de uma rede neural.
Vamos analisar melhor algumas funções de ativação comuns que você deve encontrar ao ler artigos de pesquisa e códigos de outras pessoas.
Sigmoide
A função sigmoide é caracterizada por uma curva em forma de "S" que assume apenas valores entre zero e um. É uma função diferenciável, ou seja, é possível encontrar a inclinação da curva em dois pontos quaisquer, e monotônica, o que significa que não é nem totalmente crescente nem decrescente. Normalmente, a função de ativação sigmoide é usada em problemas de classificação binária.
Veja como você pode visualizar sua própria função sigmoide usando Python:
# Sigmoid function in Python
import matplotlib.pyplot as plt
import numpy as np
x = np.linspace(-5, 5, 50)
z = 1/(1 + np.exp(-x))
plt.subplots(figsize=(8, 5))
plt.plot(x, z)
plt.grid()
plt.show()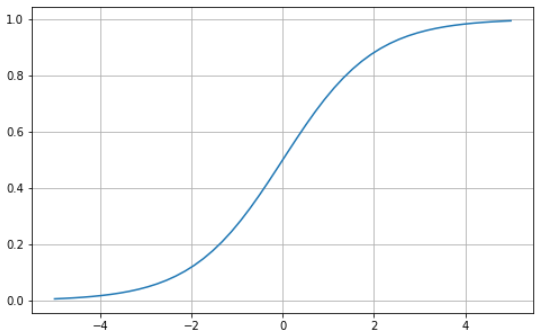
Tanh
A tangente hiperbólica (tanh) tem a mesma curva em forma de "S" que a função sigmoide, mas os valores ficam entre -1 e 1. Assim, entradas pequenas são mapeadas mais próximas de -1, e entradas maiores são mapeadas mais próximas de 1.
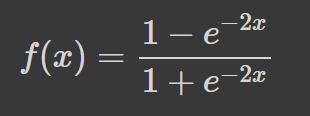
Aqui vai um exemplo da função tanh visualizada usando Python:
# tanh function in Python
import matplotlib.pyplot as plt
import numpy as np
x = np.linspace(-5, 5, 50)
z = np.tanh(x)
plt.subplots(figsize=(8, 5))
plt.plot(x, z)
plt.grid()
plt.show()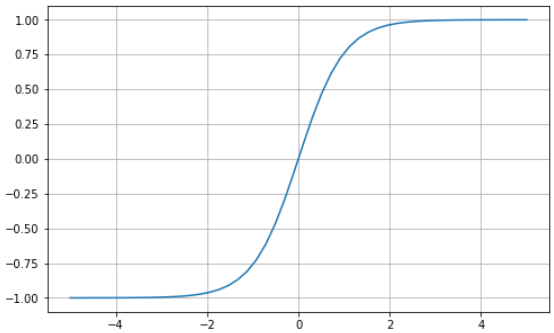
Softmax
A função softmax costuma ser usada como função de ativação na camada de saída. É uma generalização da função sigmoide para várias dimensões. Assim, é usada em redes neurais para prever a qual classe um elemento pertence com base em mais de dois rótulos.
Unidade linear retificada (ReLU)
O uso da função sigmoide ou tanh para criar redes neurais profundas é arriscado, pois é mais provável que sofram com o problema da dissipação do gradiente. A unidade linear retificada (ReLU, Rectified Linear Unit) é uma função de ativação criada como solução para esse problema e costuma ser a função de ativação padrão em várias redes neurais.
Aqui vai um exemplo visual da função ReLU usando Python:
# ReLU in Python
import matplotlib.pyplot as plt
import numpy as np
x = np.linspace(-5, 5, 50)
z = [max(0, i) for i in x]
plt.subplots(figsize=(8, 5))
plt.plot(x, z)
plt.grid()
plt.show()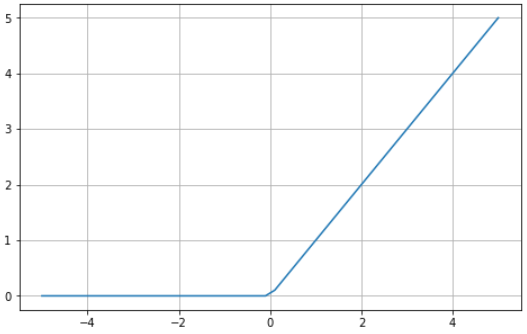
A ReLU assume valores entre zero e infinito. Observe que, para valores de entrada menores ou iguais a zero, a função retorna zero e, para valores acima de zero, a função retorna o valor de entrada fornecido (ou seja, se você inserir 2, será retornado 2). A função ReLU acaba se comportando de forma extremamente semelhante a uma função linear, o que a torna muito mais fácil de otimizar e implementar.
O processo da camada de entrada até a camada de saída é conhecido como passagem para frente ou propagação para frente. Durante essa fase, as saídas geradas pelo modelo são usadas para calcular uma função de custo a fim de identificar o desempenho da rede neural após cada iteração. Essas informações são então repassadas ao modelo para corrigir os pesos, de modo que o modelo possa fazer previsões melhores em um processo conhecido como retropropagação.
Retropropagação
No final da primeira passagem para frente, a rede faz previsões usando os pesos inicializados, que não foram ajustados. Portanto, é muito provável que as previsões feitas pelo modelo não sejam precisas. Usando a perda calculada na propagação para frente, passamos informações de volta pela rede a fim de ajustar os pesos em um processo conhecido como retropropagação.
Por fim, usamos a função de otimização para ajudar a identificar os pesos que podem reduzir a taxa de erro, tornando o modelo mais confiável e aumentando sua capacidade de generalização para novas instâncias. A matemática de como isso funciona está além do escopo deste artigo, mas o leitor interessado pode aprender mais sobre retropropagação em nosso curso Introdução ao Aprendizado Profundo em Python.
Tutorial de PyTorch: explicação passo a passo de como criar uma rede neural desde o início
Nesta seção do artigo, vamos criar um modelo simples de rede neural artificial usando a biblioteca PyTorch. Confira este espaço de trabalho do DataCamp para acompanhar o código
O PyTorch é uma das bibliotecas mais conhecidas para aprendizado profundo. Ele oferece uma experiência de depuração muito mais direta do que o TensorFlow. O PyTorch tem várias outras vantagens, como treinamento distribuído, um ecossistema robusto, suporte à nuvem, permitindo que você escreva códigos prontos para produção, etc. Para saber mais sobre o PyTorch, confira o programa de habilidades Introdução ao aprendizado profundo com o PyTorch.
Vamos começar o tutorial.
Definição e preparação dos dados
O conjunto de dados que usaremos em nosso tutorial é o make_circles, do scikit-learn. Consulte a documentação. Trata-se de um conjunto de dados sobre brinquedos que contém um círculo grande com um círculo menor em um plano bidimensional e duas variáveis independentes. Em nossa demonstração, usamos 10.000 amostras e adicionamos um ruído gaussiano com desvio-padrão de 0,05 aos dados.
Antes de criarmos a rede neural, é uma boa prática dividir os dados em conjuntos de treinamento e teste para poder avaliar o desempenho do modelo em dados não vistos.
import matplotlib.pyplot as plt
from sklearn.datasets import make_circles
from sklearn.model_selection import train_test_split
# Create a dataset with 10,000 samples.
X, y = make_circles(n_samples = 10000,
noise= 0.05,
random_state=26)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=.33, random_state=26)
# Visualize the data.
fig, (train_ax, test_ax) = plt.subplots(ncols=2, sharex=True, sharey=True, figsize=(10, 5))
train_ax.scatter(X_train[:, 0], X_train[:, 1], c=y_train, cmap=plt.cm.Spectral)
train_ax.set_title("Training Data")
train_ax.set_xlabel("Feature #0")
train_ax.set_ylabel("Feature #1")
test_ax.scatter(X_test[:, 0], X_test[:, 1], c=y_test)
test_ax.set_xlabel("Feature #0")
test_ax.set_title("Testing data")
plt.show()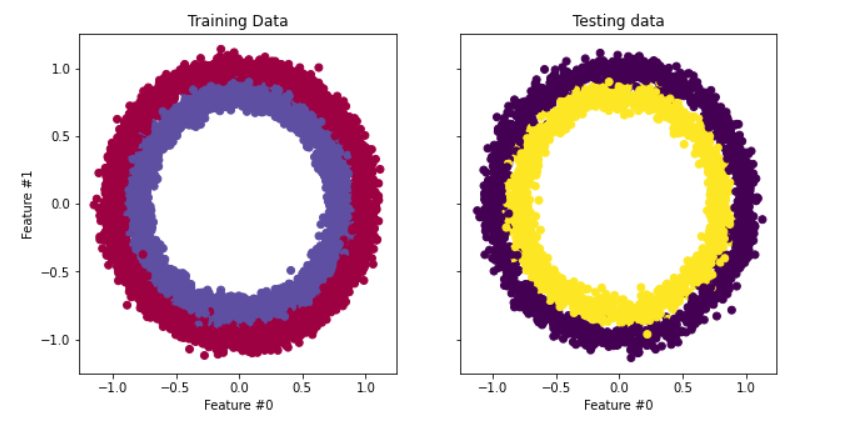
A próxima etapa é converter os dados de treinamento e teste de matrizes NumPy em tensores PyTorch. Para isso, vamos criar um conjunto de dados personalizado para nossos arquivos de treinamento e teste. Também vamos utilizar o módulo Dataloader do PyTorch para poder treinar os dados em lotes. Aqui está o código:
import warnings
warnings.filterwarnings("ignore")
!pip install torch -q
import torch
import numpy as np
from torch.utils.data import Dataset, DataLoader
# Convert data to torch tensors
class Data(Dataset):
def __init__(self, X, y):
self.X = torch.from_numpy(X.astype(np.float32))
self.y = torch.from_numpy(y.astype(np.float32))
self.len = self.X.shape[0]
def __getitem__(self, index):
return self.X[index], self.y[index]
def __len__(self):
return self.len
batch_size = 64
# Instantiate training and test data
train_data = Data(X_train, y_train)
train_dataloader = DataLoader(dataset=train_data, batch_size=batch_size, shuffle=True)
test_data = Data(X_test, y_test)
test_dataloader = DataLoader(dataset=test_data, batch_size=batch_size, shuffle=True)
# Check it's working
for batch, (X, y) in enumerate(train_dataloader):
print(f"Batch: {batch+1}")
print(f"X shape: {X.shape}")
print(f"y shape: {y.shape}")
break
"""
Batch: 1
X shape: torch.Size([64, 2])
y shape: torch.Size([64])
"""Agora vamos implementar e treinar a rede neural.
Implementação da rede neural e treinamento do modelo
Vamos implementar uma rede neural simples de duas camadas que usa a função de ativação ReLU (torch.nn.functional.relu). Para isso, vamos criar uma classe chamada NeuralNetwork que herda as propriedades de nn.Module, a classe base para todos os módulos de rede neural criados no PyTorch.
Aqui está o código:
import torch
from torch import nn
from torch import optim
input_dim = 2
hidden_dim = 10
output_dim = 1
class NeuralNetwork(nn.Module):
def __init__(self, input_dim, hidden_dim, output_dim):
super(NeuralNetwork, self).__init__()
self.layer_1 = nn.Linear(input_dim, hidden_dim)
nn.init.kaiming_uniform_(self.layer_1.weight, nonlinearity="relu")
self.layer_2 = nn.Linear(hidden_dim, output_dim)
def forward(self, x):
x = torch.nn.functional.relu(self.layer_1(x))
x = torch.nn.functional.sigmoid(self.layer_2(x))
return x
model = NeuralNetwork(input_dim, hidden_dim, output_dim)
print(model)
"""
NeuralNetwork(
(layer_1): Linear(in_features=2, out_features=10, bias=True)
(layer_2): Linear(in_features=10, out_features=1, bias=True)
)
"""Isso é tudo.
Para treinar o modelo, precisamos definir uma função de perda a ser usada para calcular os gradientes e um otimizador para atualizar os parâmetros. Em nossa demonstração, usaremos a entropia cruzada binária e um gradiente descendente estocástico com taxa de aprendizado de 0,1.
learning_rate = 0.1
loss_fn = nn.BCELoss()
optimizer = torch.optim.SGD(model.parameters(), lr=leaVamos treinar o modelo
num_epochs = 100
loss_values = []
for epoch in range(num_epochs):
for X, y in train_dataloader:
# zero the parameter gradients
optimizer.zero_grad()
# forward + backward + optimize
pred = model(X)
loss = loss_fn(pred, y.unsqueeze(-1))
loss_values.append(loss.item())
loss.backward()
optimizer.step()
print("Training Complete")
"""
Training Complete
"""Como monitoramos os valores de perda, podemos visualizar a perda do modelo ao longo do tempo.
step = np.linspace(0, 100, 10500)
fig, ax = plt.subplots(figsize=(8,5))
plt.plot(step, np.array(loss_values))
plt.title("Step-wise Loss")
plt.xlabel("Epochs")
plt.ylabel("Loss")
plt.show()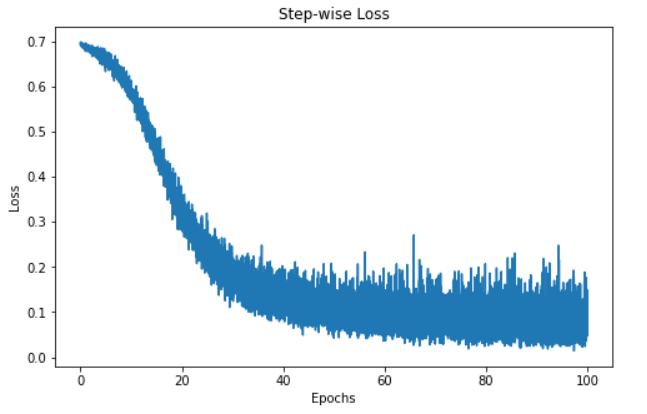
A visualização acima mostra a perda do modelo em 100 épocas. Inicialmente, a perda começa em 0,7 e diminui gradualmente. Isso indica que o modelo está melhorando as previsões ao longo do tempo. No entanto, o modelo parece atingir um patamar em torno da marca de 60 épocas, o que pode ter uma série de motivos, como o fato de o modelo estar na região de um mínimo local ou global da função de perda.
Contudo, o modelo foi treinado e está pronto para fazer previsões sobre novas instâncias – vamos ver como fazer isso na próxima seção.
Previsões e avaliação do modelo
Fazer previsões com nossa rede neural PyTorch é bem simples.
"""
We're not training so we don't need to calculate the gradients for our outputs
"""
with torch.no_grad():
for X, y in test_dataloader:
outputs = model(X)
predicted = np.where(outputs < 0.5, 0, 1)
predicted = list(itertools.chain(*predicted))
y_pred.append(predicted)
y_test.append(y)
total += y.size(0)
correct += (predicted == y.numpy()).sum().item()
print(f'Accuracy of the network on the 3300 test instances: {100 * correct // total}%')
"""
Accuracy of the network on the 3300 test instances: 97%
"""Observação: cada execução do código gera uma saída diferente, portanto talvez você não obtenha os mesmos resultados.
O código acima faz um loop pelos lotes de teste, que são armazenados na variável test_dataloader, sem calcular os gradientes. Em seguida, prevemos as instâncias no lote e armazenamos os resultados em uma variável chamada outputs. Depois disso, definimos todos os valores menores que 0,5 como 0 e aqueles iguais ou maiores que 0,5 como 1. Em seguida, esses valores são anexados a uma lista para nossas previsões.
Depois disso, adicionamos as previsões reais das instâncias no lote a uma variável chamada total. Na sequência, calculamos o número de previsões corretas identificando o número de previsões iguais às classes reais e totalizando-as. O número total de previsões corretas para cada lote é incrementado e armazenado em nossa variável correct.
Para calcular a precisão do modelo como um todo, multiplicamos o número de previsões corretas por 100 (para obter uma porcentagem) e, em seguida, dividimos pelo número de instâncias em nosso conjunto de teste. Nosso modelo teve 97% de precisão. Continuamos a análise usando a matriz de confusão e o classification_report do scikit-learn para entender melhor o desempenho do modelo.
from sklearn.metrics import classification_report
from sklearn.metrics import confusion_matrix
import seaborn as sns
y_pred = list(itertools.chain(*y_pred))
y_test = list(itertools.chain(*y_test))
print(classification_report(y_test, y_pred))
"""
precision recall f1-score support
0.0 0.98 0.97 0.98 1635
1.0 0.98 0.98 0.98 1665
accuracy 0.98 3300
macro avg 0.98 0.98 0.98 3300
weighted avg 0.98 0.98 0.98 3300
"""
cf_matrix = confusion_matrix(y_test, y_pred)
plt.subplots(figsize=(8, 5))
sns.heatmap(cf_matrix, annot=True, cbar=False, fmt="g")
plt.show()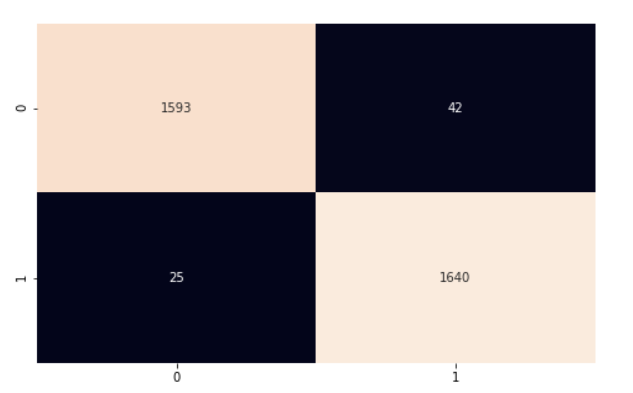
Nosso modelo está funcionando muito bem. Incentivo você a analisar o código e fazer algumas alterações para assimilar o que foi abordado neste artigo.
Neste tutorial do PyTorch, abordamos os fundamentos básicos das redes neurais e usamos o PyTorch, uma biblioteca Python para aprendizado profundo, na implementação de nossa rede. Usamos o conjunto de dados do circles do scikit-learn para treinar uma rede neural de duas camadas para classificação. Em seguida, fizemos previsões sobre os dados e avaliamos os resultados usando a métrica de precisão.