Tutorial de Redes Neuronales Convolucionales (CNN) con TensorFlow

Imagina que estás en un zoo intentando reconocer si un determinado animal es un guepardo o un leopardo. Como humano, tu cerebro puede analizar sin esfuerzo los rasgos corporales y faciales para llegar a una conclusión válida. Del mismo modo, las Redes Neuronales Convolucionales (CNN) pueden entrenarse para realizar la misma tarea de reconocimiento, independientemente de la complejidad de los patrones. Esto las hace potentes en el campo de la visión por ordenador. 

Este tutorial conceptual sobre las CNN comenzará proporcionando una visión general de lo que son las CNN y de su importancia en el aprendizaje automático. A continuación, te guiará paso a paso en la implementación de CNN en TensorFlow Framework 2.

¿Qué es una CNN?

Una Red Neuronal Convolucional (CNN o ConvNet) es un algoritmo de aprendizaje profundo diseñado específicamente para cualquier tarea en la que el reconocimiento de objetos sea crucial, como la clasificación, detección y segmentación de imágenes.  Muchas aplicaciones de la vida real, como los coches autoconducidos, las cámaras de vigilancia, etc., utilizan CNN. 

La importancia de las CNN

Hay varias razones por las que las CNN son importantes, como se destaca a continuación:

• A diferencia de los modelos tradicionales de aprendizaje automático, como SVM y los árboles de decisión, que requieren extracciones manuales de características, las CNN pueden realizar extracciones automáticas de características a escala, lo que las hace eficientes. 
• Las capas de convoluciones hacen que las CNN sean invariantes a la traslación, lo que significa que pueden reconocer patrones de los datos y extraer características independientemente de su posición, tanto si la imagen está girada, escalada o desplazada.
• Se ha demostrado que múltiples modelos CNN preentrenados, como VGG-16, ResNet50, Inceptionv3 y EfficientNet, han alcanzado resultados de vanguardia y pueden ajustarse en tareas de noticias utilizando una cantidad relativamente pequeña de datos. 
• Las CNN también pueden utilizarse para problemas de clasificación que no sean de imágenes y no se limitan al procesamiento del lenguaje natural, el análisis de series temporales y el reconocimiento del habla.

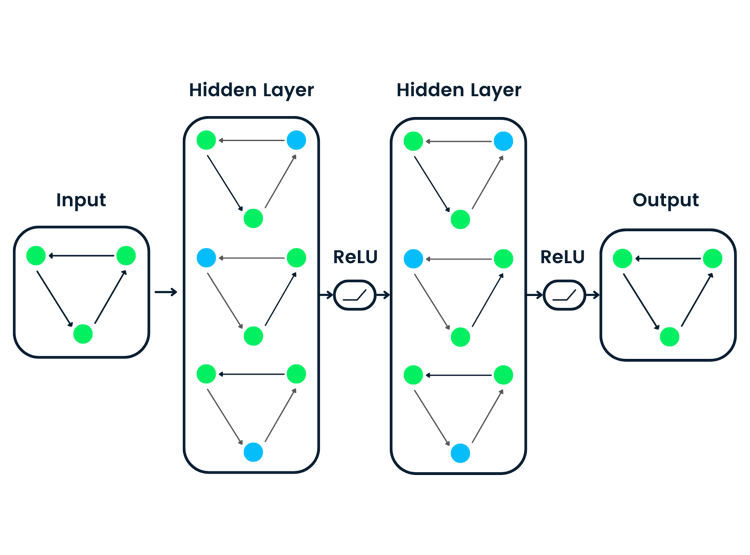
Arquitectura de una CNN

La arquitectura de las CNN intenta imitar la estructura de las neuronas del sistema visual humano, compuestas por múltiples capas, en las que cada una es responsable de detectar una característica específica en los datos.  Como se ilustra en la imagen siguiente, la CNN típica está formada por una combinación de cuatro capas principales: 

• Capas convolucionales
• Unidad lineal rectificada (abreviado ReLU)
• Puesta en común de capas
• Capas totalmente conectadas 

Comprendamos cómo funciona cada una de estas capas utilizando el siguiente ejemplo de clasificación del dígito manuscrito.

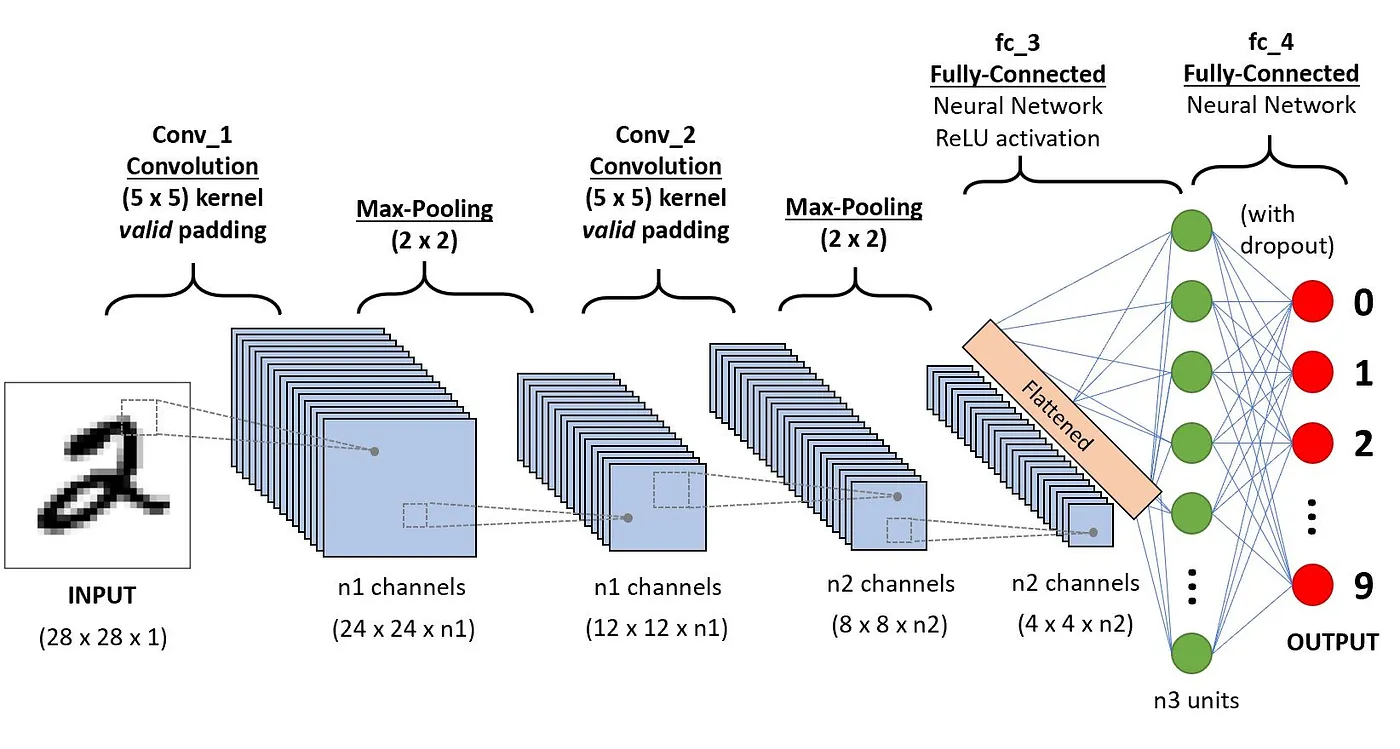
Capas de convolución

Este es el primer bloque de construcción de una CNN. Como su nombre indica, la principal tarea matemática que se realiza se llama convolución, que es la aplicación de una función de ventana deslizante a una matriz de píxeles que representa una imagen. La función de deslizamiento aplicada a la matriz se denomina núcleo o filtro, y ambos pueden utilizarse indistintamente. 

En la capa de convolución, se aplican varios filtros de igual tamaño, y cada filtro se utiliza para reconocer un patrón específico de la imagen, como la curvatura de los dígitos, los bordes, la forma completa de los dígitos, etc. 

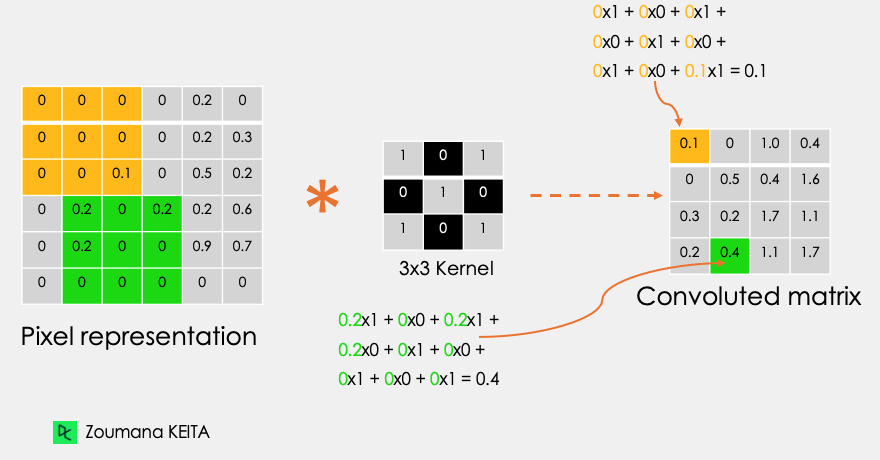
Consideremos esta imagen en escala de grises de 32x32 de un dígito manuscrito. Los valores de la matriz se dan a título ilustrativo.

Además, consideremos el núcleo utilizado para la convolución. Es una matriz de dimensión 3x3. Los pesos de cada elemento del núcleo se representan en la cuadrícula. Los pesos cero se representan en las cuadrículas negras y los unos en la cuadrícula blanca. 

¿Tenemos que encontrar manualmente estos pesos? 

En la vida real, los pesos de los núcleos se determinan durante el proceso de entrenamiento de la red neuronal. 

Utilizando estas dos matrices, podemos realizar la operación de convolución tomando aplicando el producto punto, y trabajar de la siguiente manera: 

1. Aplica la matriz del núcleo desde la esquina superior izquierda hacia la derecha.
2. Realiza la multiplicación por elementos.  
3. Suma los valores de los productos.
4. El valor resultante corresponde al primer valor (esquina superior izquierda) de la matriz convolucionada.
5. Desplaza el núcleo hacia abajo con respecto al tamaño de la ventana deslizante.
6. Repite del paso 1 al 5 hasta que la matriz de imagen esté totalmente cubierta.

La dimensión de la matriz convoluta depende del tamaño de la ventana deslizante. Cuanto mayor sea la ventana deslizante, menor será la dimensión.

Otro nombre asociado al núcleo en la literatura es detector de rasgos, porque los pesos pueden ajustarse con precisión para detectar rasgos específicos en la imagen de entrada. 

Por ejemplo: 

• El núcleo de píxeles vecinos promediados puede utilizarse para difuminar la imagen de entrada.
• La sustracción del núcleo vecino se utiliza para realizar la detección de bordes.

Cuantas más capas de convolución tenga la red, mejor será la capa para detectar rasgos más abstractos. 

Función de activación

Se aplica una función de activación ReLU después de cada operación de convolución. Esta función ayuda a la red a aprender relaciones no lineales entre las características de la imagen, lo que la hace más robusta para identificar distintos patrones. También ayuda a mitigar los problemas de gradiente evanescente. 

Capa de agrupamiento

El objetivo de la capa de agrupación es extraer los rasgos más significativos de la matriz convoluta. Esto se hace aplicando algunas operaciones de agregación, que reducen la dimensión del mapa de características (matriz convoluta), reduciendo así la memoria utilizada durante el entrenamiento de la red.  La agrupación también es relevante para mitigar el sobreajuste.

Las funciones de agregación más comunes que pueden aplicarse son: 

• Max pooling que es el valor máximo del mapa de características
• La agrupación de sumas corresponde a la suma de todos los valores del mapa de características
• La agrupación media es la media de todos los valores. 

A continuación se ilustra cada uno de los ejemplos anteriores: 

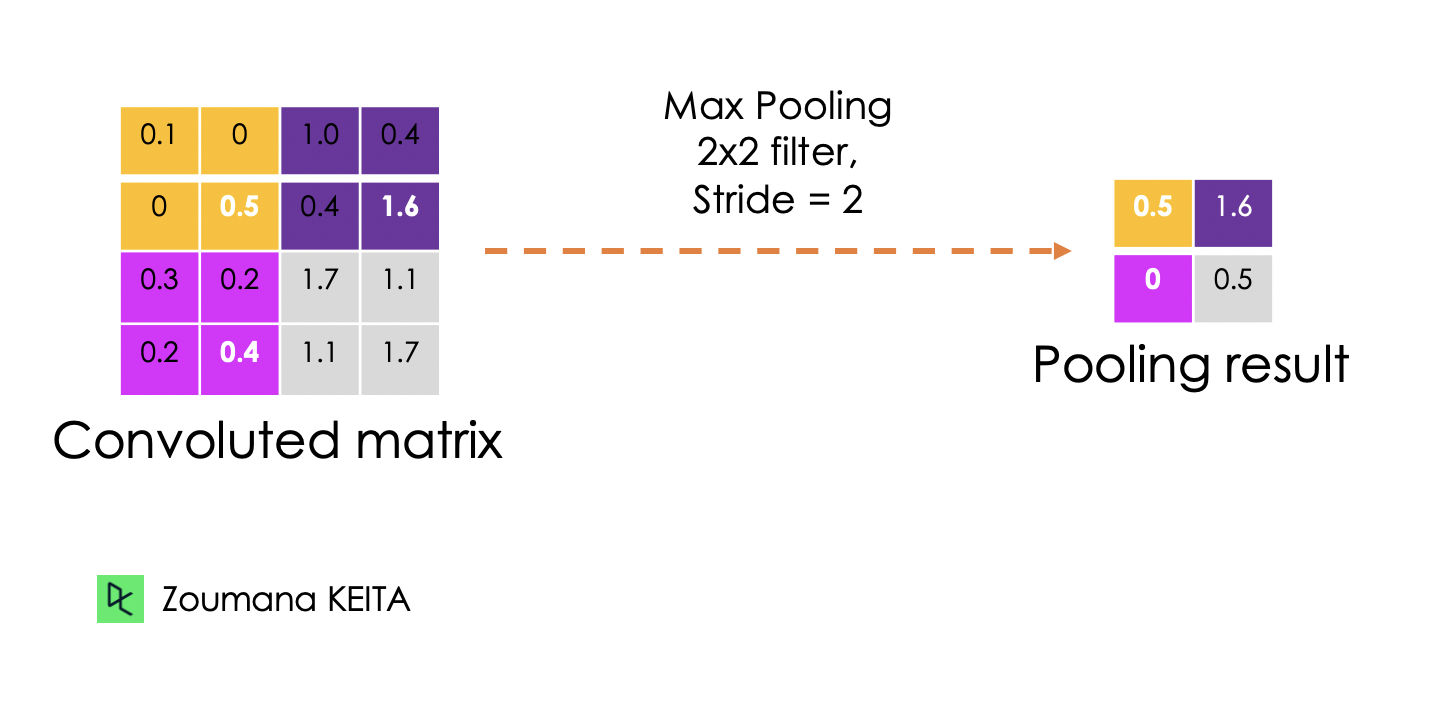
Además, la dimensión del mapa de características se reduce a medida que se aplica la función de sondeo. 

La última capa de agrupación aplana su mapa de características para que pueda ser procesado por la capa totalmente conectada. 

Capas totalmente conectadas

Estas capas están en la última capa de la red neuronal convolucional, y sus entradas corresponden a la matriz unidimensional aplanada generada por la última capa de agrupamiento. Se les aplican funciones de activación ReLU para la no linealidad. 

Por último, se utiliza una capa de predicción softmax para generar valores de probabilidad para cada una de las posibles etiquetas de salida, y la etiqueta final predicha es la que tiene la puntuación de probabilidad más alta. 

Abandono 

El Dropout es una técnica de regularización que se aplica para mejorar la capacidad de generalización de las redes neuronales con un gran número de parámetros. Consiste en descartar aleatoriamente algunas neuronas durante el proceso de entrenamiento, lo que obliga a las neuronas restantes a aprender nuevas características a partir de los datos de entrada.  

Dado que la implementación técnica se realizará utilizando TensorFlow 2, la siguiente sección tiene como objetivo proporcionar una visión completa de los diferentes componentes de este marco para construir eficientemente modelos de aprendizaje profundo. 

¿Qué es el marco TensorFlow?

Google desarrolló TensorFlow en noviembre de 2015. Lo definen como un marco de aprendizaje automático de código abierto para todos por varias razones. 

• Código abierto: publicado bajo la licencia Apache 2.0 de código abierto. Esto permite a investigadores, organizaciones y desarrolladores hacer su contribución a la biblioteca construyendo sobre ella sin ninguna restricción. 
• Marco de aprendizaje automático: lo que significa que dispone de un conjunto de bibliotecas y herramientas que apoyan el proceso de construcción de modelos de aprendizaje automático.
• Para todos: El uso de TensorFlow facilita la implementación de modelos de aprendizaje automático mediante lenguajes de programación comunes como Python. Además, bibliotecas integradas como Keras facilitan aún más la creación de modelos sólidos de aprendizaje profundo. 

Todas estas funcionalidades hacen de Tensorflow un buen candidato para construir redes neuronales. 

Además, la instalación de Tensorflow 2 es sencilla y puede realizarse de la siguiente manera utilizando el gestor de paquetes de Python pip como se explica en la documentación oficial.

Tras la instalación, podemos ver que la versión utilizada es la 2.9.1

import tensorflow as tf
print("TensorFlow version:", tf.__version__)

Ahora, vamos a explorar más a fondo los componentes principales para crear esas redes. 

¿Qué son los Tensores?

Cuando construimos modelos de aprendizaje automático y aprendizaje profundo, nos enfrentamos principalmente a datos de alta dimensión. Los tensores son matrices multidimensionales con un tipo uniforme que se utilizan para representar distintas características de los datos. 

A continuación se muestra la representación gráfica de los distintos tipos de dimensiones de los tensores. 

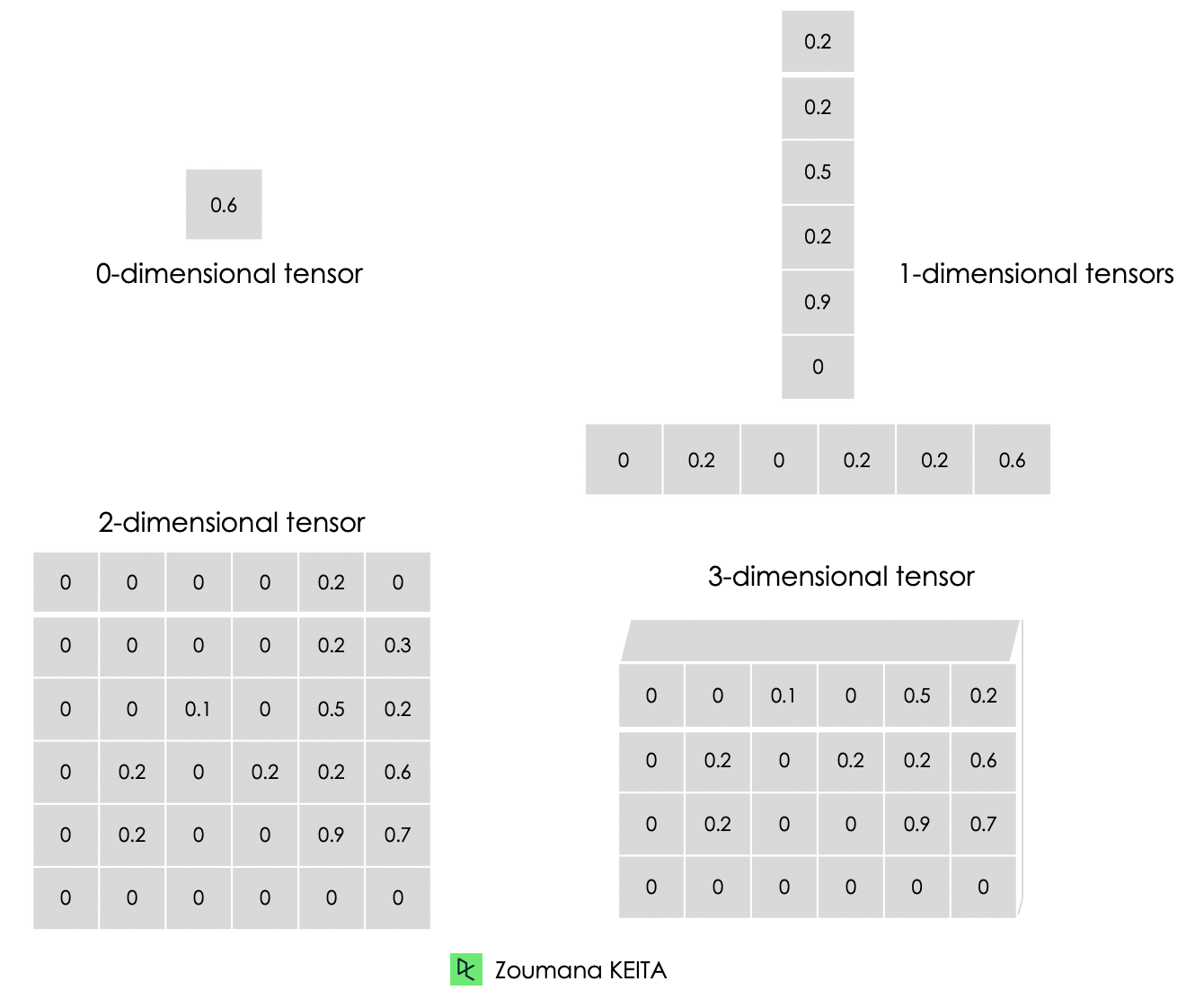
• Un tensor de 0 dimensiones contiene un único valor.
• Un tensor unidimensional, también conocido como tensor de "rango 1", es una lista de valores. 
• Un tensor bidimensional es un tensor de "rango 2".
• Por último, podemos tener un tensor de N dimensiones, donde N representa el número de dimensiones dentro del tensor. En los casos anteriores, N es respectivamente 0, 1 y 2.

A continuación se muestra una ilustración de un cero a un tensor tridimensional. Cada tensor se crea utilizando la función constant() de TensorFlow. 

# Zero dimensional tensor
zero_dim_tensor = tf.constant(20)
print(zero_dim_tensor)

# One dimensional tensor
one_dim_tensor = tf.constant([12, 20, 53, 26, 11, 56])
print(one_dim_tensor)

# Two dimensional tensor
two_dim_array = [[3, 6, 7, 5],
             	[9, 2, 3, 4],
             	[7, 1, 10,6],
             	[0, 8, 11,2]]

two_dim_tensor = tf.constant(two_dim_array)
print(two_dim_tensor)

Una ejecución correcta del código anterior debería generar los resultados que aparecen a continuación, y podemos observar la palabra clave "tf.Tensor" para significar que el resultado es un tensor. Tiene tres parámetros:

•  El valor real del tensor.
• La función forma() del tensor, que es 0, 6 por 1 y 4 por 4, respectivamente para el primer, segundo y tercer tensores.
• El tipo de datos representado por dtype y todos los tensores son int32.

Nuestro Tutorial de Tensorflow para principiantes proporciona una visión completa de TensorFlow y enseña a construir y entrenar modelos.

Tensores frente a matrices: Diferencias

Mucha gente confunde los tensores con las matrices. Aunque estos dos objetos se parecen, tienen propiedades completamente distintas. Esta sección permite comprender mejor la diferencia entre matrices y tensores.

• Podemos pensar en una matriz como un tensor de sólo dos dimensiones. 
• Los Tensores, en cambio, son un formato más general que puede tener cualquier número de dimensiones.

A diferencia de las matrices, los tensores son más adecuados para los problemas de aprendizaje profundo por las siguientes razones: 

• Pueden tratar cualquier número de dimensiones, por lo que se adaptan mejor a los datos multidimensionales.
• La capacidad de los tensores de ser compatibles con una amplia gama de tipos de datos, formas y dimensiones los hace más versátiles que las matrices.
• Tensorflow ofrece compatibilidad con GPU y TPU para acelerar los cálculos. Utilizando tensores, los ingenieros de aprendizaje automático pueden aprovechar automáticamente estas ventajas.
• Los tensores admiten de forma nativa la difusión, que consiste en realizar operaciones aritméticas entre tensores de formas diferentes, lo que no siempre es posible cuando se trata de matrices.  

TensorFlow: Constantes, variables y marcadores de posición

Las constantes no son los únicos tipos de tensores. También hay variables y marcadores de posición, que son los componentes básicos de un grafo computacional. 

Un grafo computacional es básicamente y una representación de una secuencia de operaciones y del flujo de datos entre ellas. 

Ahora, entendamos la diferencia entre estos tipos de tensores.

Constantes

Las constantes son tensores cuyos valores no cambian durante la ejecución del gráfico de cálculo. Se crean utilizando la función tf.constant() y se utilizan principalmente para almacenar parámetros fijos que no requieren ningún cambio durante el entrenamiento del modelo.

Variables

Las variables son tensores cuyo valor puede modificarse durante la ejecución del gráfico de cálculo y se crean mediante la funcióntf.Variable(). Por ejemplo, en el caso de las redes neuronales, los pesos y los sesgos pueden definirse como variables, ya que deben actualizarse durante el proceso de entrenamiento. 

Marcadores de posición

Se utilizaron en la primera versión de Tensorflow como contenedores vacíos que no tienen valores específicos. Sólo se utilizan para invertir un lugar para los datos que se utilizarán en el futuro. Esto da a los usuarios la libertad de utilizar diferentes conjuntos de datos y tamaños de lote durante el entrenamiento y la validación del modelo.

En la versión 2 de Tensorflow, los marcadores de posición se han sustituido por la función tf.function() que es un enfoque más pitónico y dinámico para introducir datos en el grafo computacional.

Implementación paso a paso de la CNN

Pongamos en práctica todo lo que hemos aprendido anteriormente. Esta sección ilustrará la implementación de extremo a extremo de una red neuronal convolucional en TensorFlow aplicada al conjunto de datos CIFAR-10, que es un conjunto de datos incorporado con las siguientes propiedades: 

• Contiene 60.000 imágenes en color de 32 por 32
• El conjunto de datos tiene 10 clases diferentes
• Cada clase tiene 6000 imágenes
• En total hay 50.000 imágenes de entrenamiento 
• Y en total 10.000 imágenes de prueba

El código fuente del artículo está disponible en el espacio de trabajo de DataCamp

Arquitectura de la red

Antes de entrar en la implementación técnica, entendamos primero la arquitectura general de la red que se está implementando. 

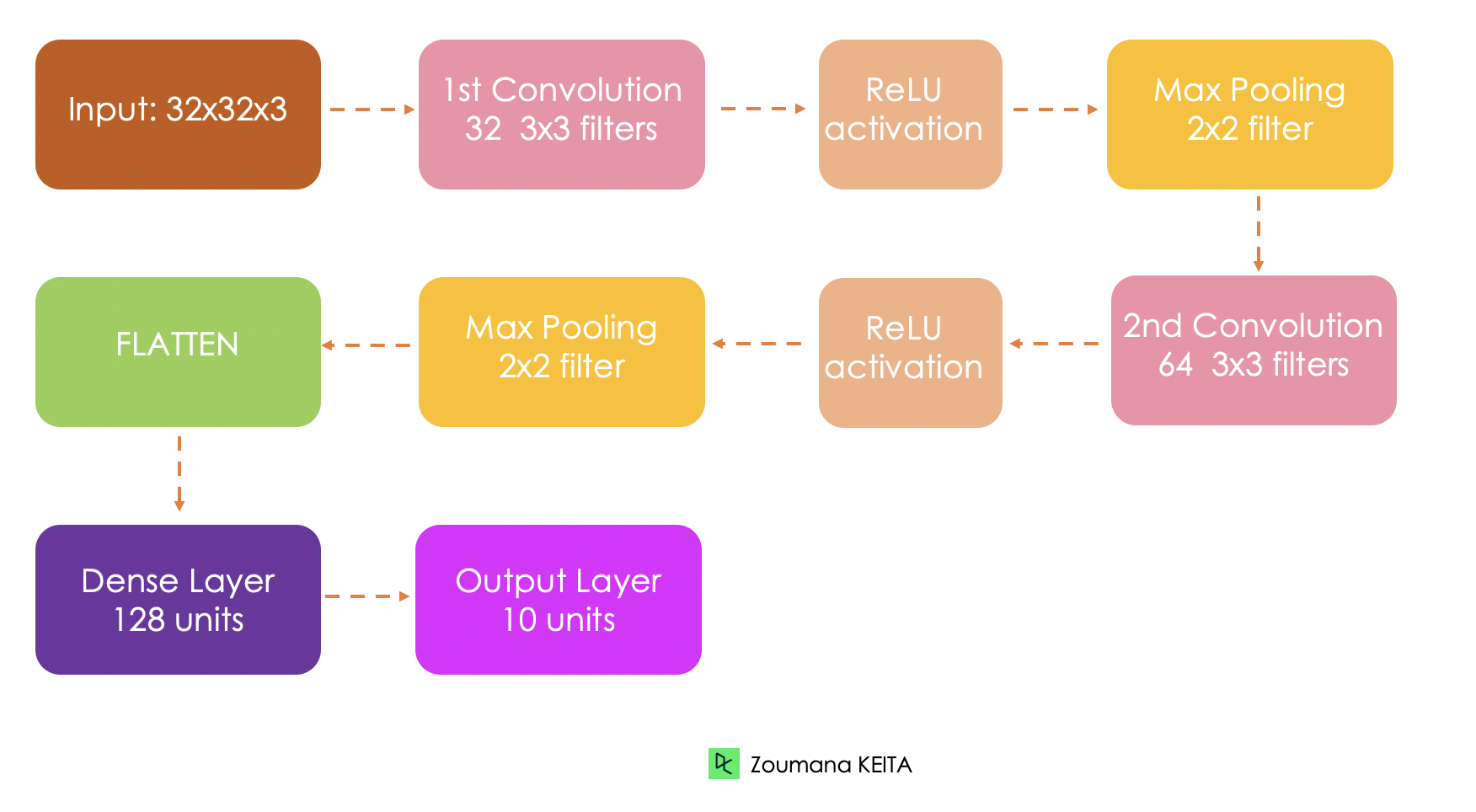
• La entrada del modelo es un tensor de 32x32x3, respectivamente, para la anchura, la altura y los canales. 
• Tendremos dos capas convolucionales. La primera capa aplica 32 filtros de tamaño 3x3 cada uno y una función de activación ReLU. Y la segunda aplica 64 filtros de tamaño 3x3
• La primera capa de agrupación aplicará una agrupación máxima de 2x2
• La segunda capa de agrupación también aplicará una agrupación máxima de 2x2
• La capa totalmente conectada tendrá 128 unidades y una función de activación ReLU
• Por último, la salida serán 10 unidades correspondientes a las 10 clases, y la función de activación es una softmax para generar las distribuciones de probabilidad.

Cargar conjunto de datos

El conjunto de datos incorporado se carga desde keras.datasets() del siguiente modo 

(train_images, train_labels), (test_images, test_labels) = cf10.load_data()

Análisis Exploratorio de Datos

En esta sección, nos centraremos únicamente en mostrar algunas imágenes de muestra, puesto que ya conocemos la proporción de cada clase tanto en los datos de entrenamiento como en los de prueba. 

La función de ayuda show_images() muestra por defecto un total de 12 imágenes y toma tres parámetros principales: 

• Las imágenes de entrenamiento
• Los nombres de las clases
• Y las etiquetas de formación.

import matplotlib.pyplot as plt

def show_images(train_images,
            	class_names,
            	train_labels,
            	nb_samples = 12, nb_row = 4):
    
	plt.figure(figsize=(12, 12))
	for i in range(nb_samples):
    	plt.subplot(nb_row, nb_row, i + 1)
    	plt.xticks([])
    	plt.yticks([])
    	plt.grid(False)
    	plt.imshow(train_images[i], cmap=plt.cm.binary)
    	plt.xlabel(class_names[train_labels[i][0]])
	plt.show()

Ahora, podemos llamar a la función con los parámetros necesarios. 

class_names = ['airplane', 'automobile', 'bird', 'cat', 'deer',
           	'dog', 'frog', 'horse', 'ship', 'truck']

show_images(train_images, class_names, train_labels)

Una ejecución correcta del código anterior genera las imágenes siguientes. 

Preprocesamiento de datos

Antes de entrenar el modelo, tenemos que normalizar los valores de los píxeles de los datos en el mismo rango (por ejemplo, de 0 a 1). Se trata de un paso de preprocesamiento habitual cuando se trabaja con imágenes, para garantizar la invariabilidad de escala y una convergencia más rápida durante el entrenamiento. 

max_pixel_value = 255

train_images = train_images / max_pixel_value
test_images = test_images / max_pixel_value

Además, observamos que las etiquetas se representan en un formato categórico como gato, caballo, pájaro, etc. Necesitamos convertirlos a un formato numérico para que puedan ser procesados fácilmente por la red neuronal.

from tensorflow.keras.utils import to_categorical
train_labels = to_categorical(train_labels, len(class_names))
test_labels = to_categorical(test_labels, len(class_names))

Implementación de la arquitectura modelo

El siguiente paso es poner en práctica la arquitectura de la red basándonos en la descripción anterior. 

En primer lugar, definimos el modelo utilizando la función Secuencial() y cada capa se añade al modelo con la función añadir() .

from tensorflow.keras import Sequential
from tensorflow.keras.layers import Conv2D, MaxPooling2D, Flatten, Dense

# Variables
INPUT_SHAPE = (32, 32, 3)
FILTER1_SIZE = 32
FILTER2_SIZE = 64
FILTER_SHAPE = (3, 3)
POOL_SHAPE = (2, 2)
FULLY_CONNECT_NUM = 128
NUM_CLASSES = len(class_names)

# Model architecture implementation
model = Sequential()
model.add(Conv2D(FILTER1_SIZE, FILTER_SHAPE, activation='relu', input_shape=INPUT_SHAPE))
model.add(MaxPooling2D(POOL_SHAPE))
model.add(Conv2D(FILTER2_SIZE, FILTER_SHAPE, activation='relu'))
model.add(MaxPooling2D(POOL_SHAPE))
model.add(Flatten())
model.add(Dense(FULLY_CONNECT_NUM, activation='relu'))
model.add(Dense(NUM_CLASSES, activation='softmax'))

Tras aplicar la función summary() al modelo, obtenemos un resumen completo de la arquitectura del modelo con información sobre cada capa, su tipo, la forma de salida y el número total de parámetros entrenables. 

Formación de modelos

Todos los recursos están finalmente disponibles para configurar y activar el entrenamiento del modelo. Esto se hace, respectivamente, con las funciones compile() y fit(), que toman los siguientes parámetros :

• El Optimizador se encarga de actualizar los pesos y sesgos del modelo. En nuestro caso, utilizamos el optimizador Adam. 
• La función de pérdida se utiliza para medir los errores de clasificación, y nosotros utilizamos la Crosentropía().
• Por último, la métrica se utiliza para medir el rendimiento del modelo, y la exactitud, la precisión y el recuerdo se mostrarán en nuestro caso práctico.

from tensorflow.keras.metrics import Precision, Recall

BATCH_SIZE = 32
EPOCHS = 30

METRICS = metrics=['accuracy',
               	Precision(name='precision'),
               	Recall(name='recall')]

model.compile(optimizer='adam',
          	loss='categorical_crossentropy',
          	metrics = METRICS)

# Train the model
training_history = model.fit(train_images, train_labels,
                	epochs=EPOCHS, batch_size=BATCH_SIZE,
                	validation_data=(test_images, test_labels))

Evaluación del modelo

Tras el entrenamiento del modelo, podemos comparar su rendimiento en los conjuntos de datos de entrenamiento y de prueba trazando las métricas anteriores mediante la función mostrar_curva_de_rendimiento() en dos dimensiones.

• El eje horizontal (x) es el número de épocas
• La vertical (y) es el rendimiento subyacente del modelo. 
• La curva representa el valor de las métricas en una época concreta.

Para una mejor visualización, se traza una línea roja vertical a través de la intersección de los valores de rendimiento de entrenamiento y validación, junto con el valor óptimo.

def show_performance_curve(training_result, metric, metric_label):
    
	train_perf = training_result.history[str(metric)]
	validation_perf = training_result.history['val_'+str(metric)]
	intersection_idx = np.argwhere(np.isclose(train_perf,
                                            	validation_perf, atol=1e-2)).flatten()[0]
	intersection_value = train_perf[intersection_idx]
    
	plt.plot(train_perf, label=metric_label)
	plt.plot(validation_perf, label = 'val_'+str(metric))
	plt.axvline(x=intersection_idx, color='r', linestyle='--', label='Intersection')
    
	plt.annotate(f'Optimal Value: {intersection_value:.4f}',
         	xy=(intersection_idx, intersection_value),
         	xycoords='data',
         	fontsize=10,
         	color='green')
            	 
	plt.xlabel('Epoch')
	plt.ylabel(metric_label)
	plt.legend(loc='lower right')

A continuación, se aplica la función tanto para la exactitud como para la precisión del modelo.

show_performance_curve(training_history, 'accuracy', 'accuracy')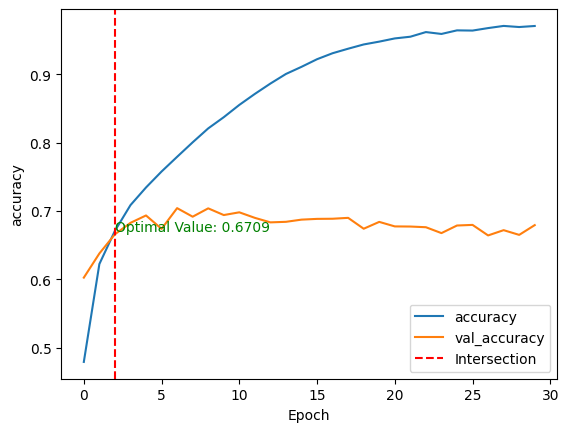

show_performance_curve(training_history, 'precision', 'precision')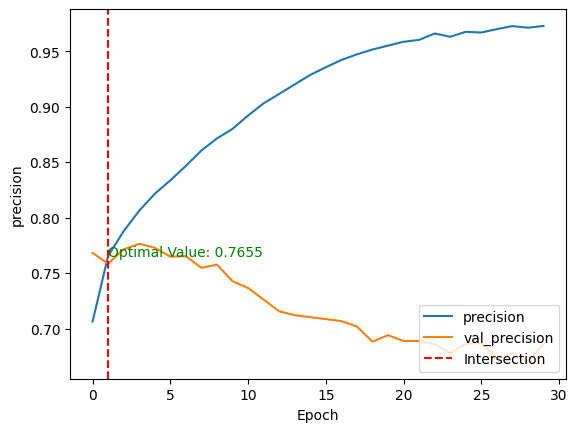

Tras entrenar el modelo sin ningún ajuste fino ni preprocesamiento, obtenemos:  

• Una puntuación de precisión del 67,09%, lo que significa que el modelo clasifica correctamente el 67% de las muestras de cada 100 muestras. 
• Y, una precisión del 76,55%, lo que significa que de cada 100 predicciones positivas, casi 77 de ellas son verdaderos positivos, y las 23 restantes son falsos positivos. 
• Estas puntuaciones se obtienen respectivamente en la tercera y segunda épocas para la exactitud y la precisión.

Estas dos métricas proporcionan una comprensión global del comportamiento del modelo. 

¿Y si queremos saber, para cada clase, cuáles son las que el modelo predice bien y aquellas con las que tiene dificultades?

Esto se puede conseguir a partir de la matriz de confusión, que muestra para cada clase el número de predicciones correctas y erróneas. La puesta en práctica se indica a continuación. Empezamos haciendo predicciones sobre los datos de prueba, luego calculamos la matriz de confusión y mostramos el resultado final.

from sklearn.metrics import confusion_matrix, ConfusionMatrixDisplay

test_predictions = model.predict(test_images)

test_predicted_labels = np.argmax(test_predictions, axis=1)

test_true_labels = np.argmax(test_labels, axis=1)

cm = confusion_matrix(test_true_labels, test_predicted_labels)

cmd = ConfusionMatrixDisplay(confusion_matrix=cm)

cmd.plot(include_values=True, cmap='viridis', ax=None, xticks_rotation='horizontal')
plt.show()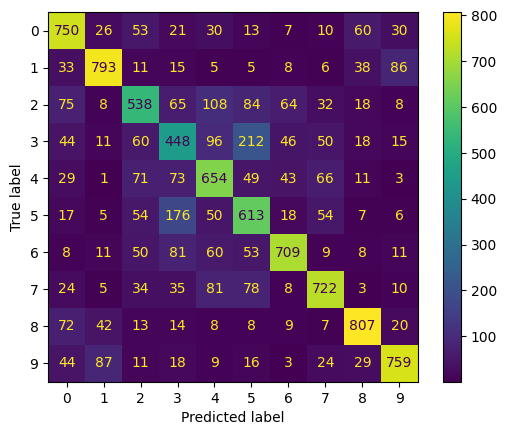

• Las clases 0, 1, 6, 7, 8, 9, respectivamente, para avión, automóvil, rana, caballo, barco y camión tienen los valores más altos en la diagonal. Esto significa que el modelo predice mejor esas clases. 
• Por otro lado, parece tener dificultades con las clases restantes:  
• Las clases con los valores fuera de diagonal más altos son aquellas con las que el modelo confunde las clases buenas. Por ejemplo, confunde pájaros (clase 2) con un avión, y automóviles con camiones (clase 9).

Aprende más sobre la matriz de confusión en nuestro tutorial Comprender la matriz de confusión en Rque toma material del curso Machine Learning toolbox de DataCamp.

Este modelo puede mejorarse con tareas adicionales como:  

• Aumento de la imagen
• Aprendizaje por transferencia utilizando modelos preentrenados como ResNet, MobileNet o VGG. Nuestra Tutorial de aprendizaje por transferencia explica qué es el aprendizaje por transferencia y algunas de sus aplicaciones en la vida real.
• Aplicando diferentes técnicas de regularización, como L1, L2 o abandono.  
• Ajuste fino de distintos hiperparámetros, como la velocidad de aprendizaje, el tamaño del lote o el número de capas de la red. 

Conclusión

Este artículo ha cubierto una visión completa de las CNN en TensorFlow, proporcionando detalles sobre cada capa de la arquitectura de las CNN. Además, hizo una breve introducción a TensorFlow y cómo ayuda a los ingenieros e investigadores de aprendizaje automático a construir redes neuronales sofisticadas. 

Aplicamos todos estos conjuntos de habilidades a un escenario del mundo real relacionado con una tarea de clasificación multiclase.  

Nuestra guía para principiantes sobre la detección de objetos puede ser un gran paso para avanzar en tu aprendizaje de la visión por ordenador. Explora los componentes clave en la detección de objetos y explica cómo implementarlos en SSD y Faster RCNN disponibles en Tensorflow.