Creación de modelos de redes neuronales (NN) en R

Introducción a las redes neuronales

Las redes neuronales o redes neuronales simuladas son un subconjunto del aprendizaje automático que se inspira en el cerebro humano. Imitan cómo las neuronas biológicas se comunican entre sí para tomar una decisión. 

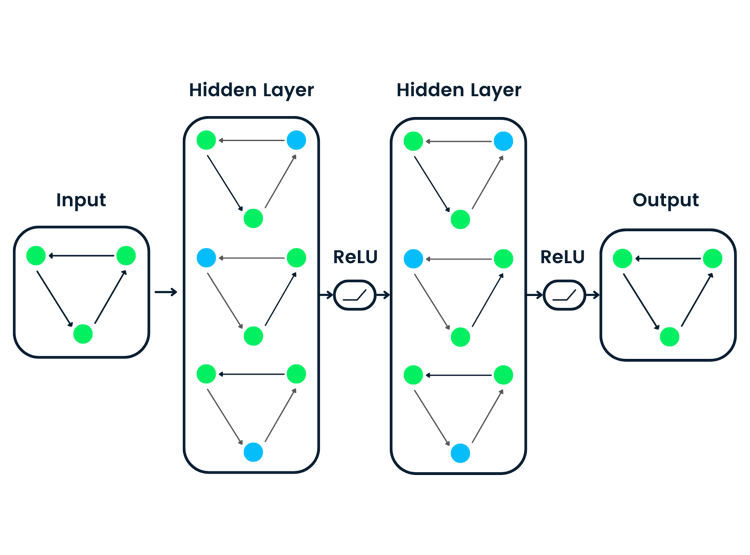
Una red neuronal consta de una capa de entrada, una capa oculta y una capa de salida. La primera capa recibe la entrada bruta, la procesan varias capas ocultas y la última produce el resultado. 

En el ejemplo siguiente, hemos simulado el proceso de entrenamiento de redes neuronales para clasificar datos tabulares. Tenemos parámetros X1 y X2 que pasan a través de 2 capas ocultas de 4 y 2 neuronas para producir la salida. Con múltiples iteraciones, el modelo mejora en la clasificación de los objetivos. 

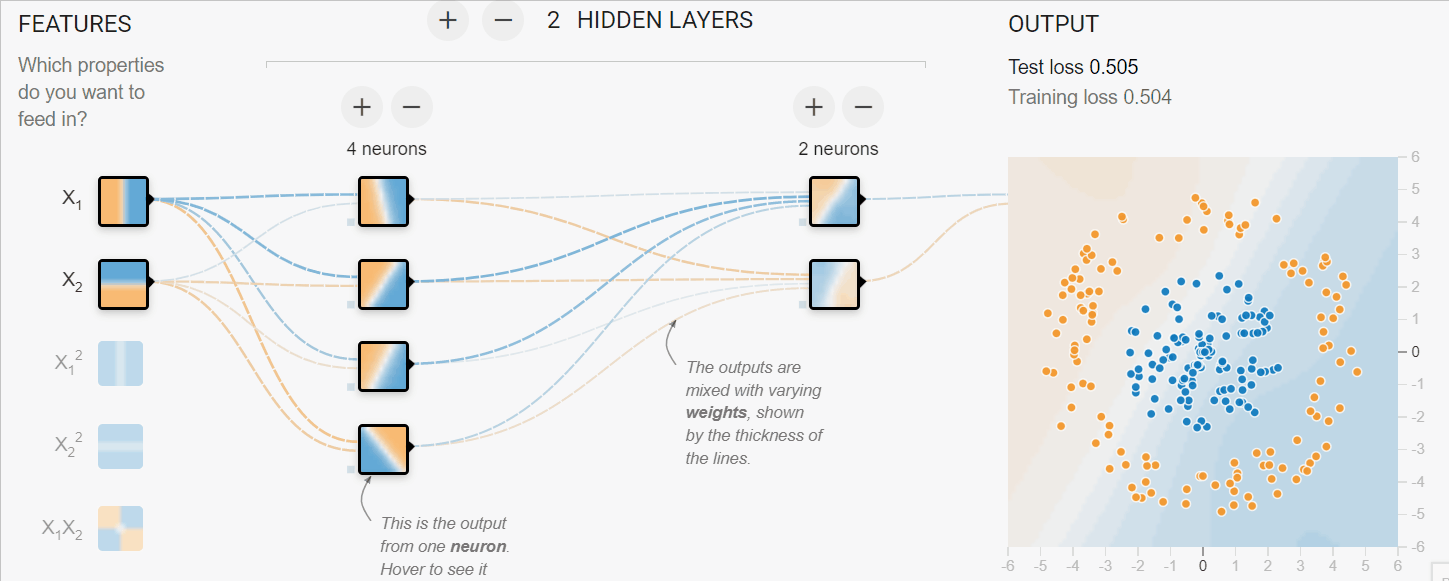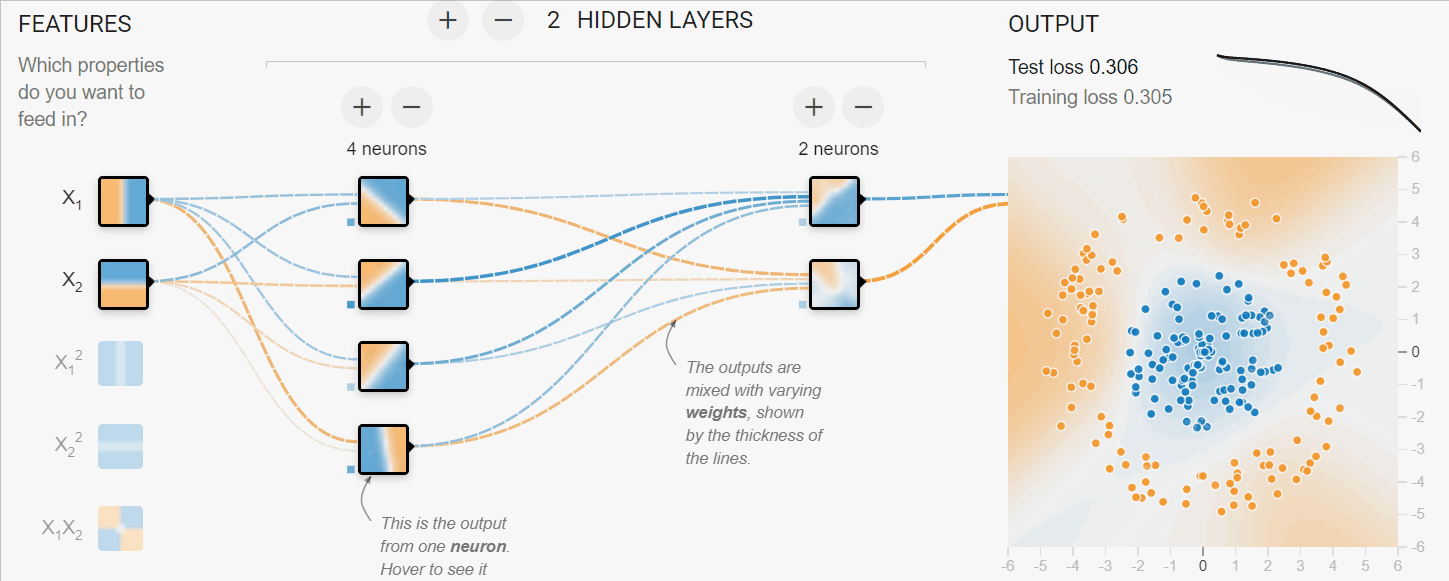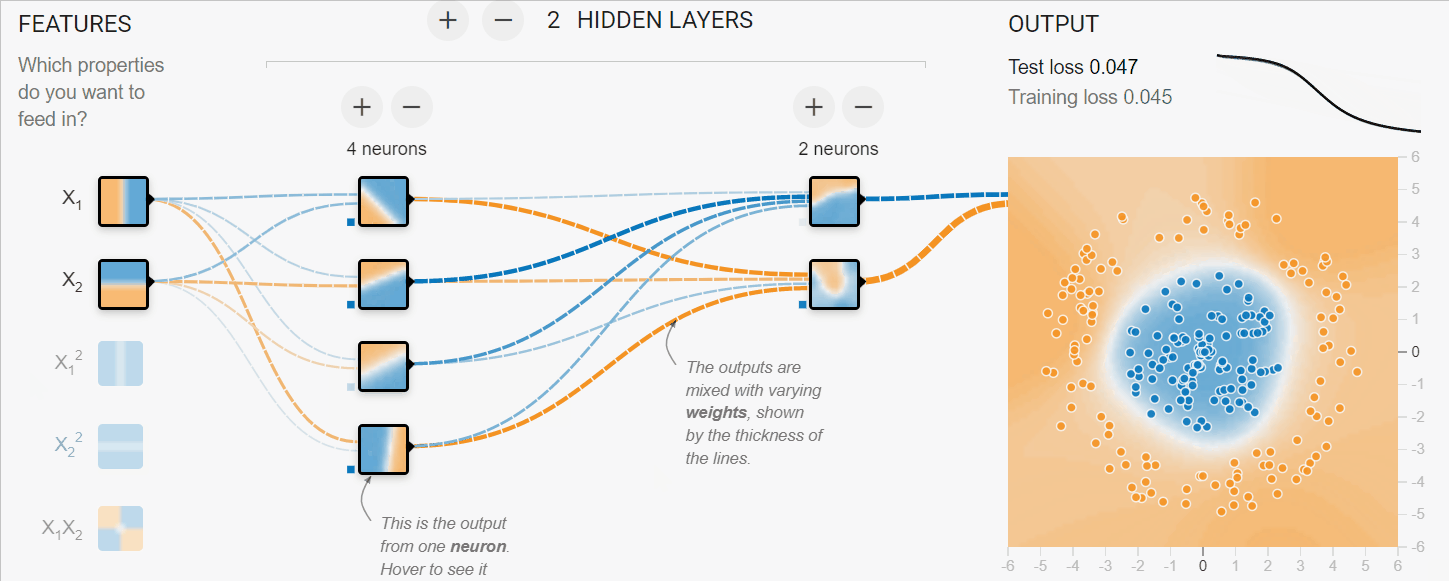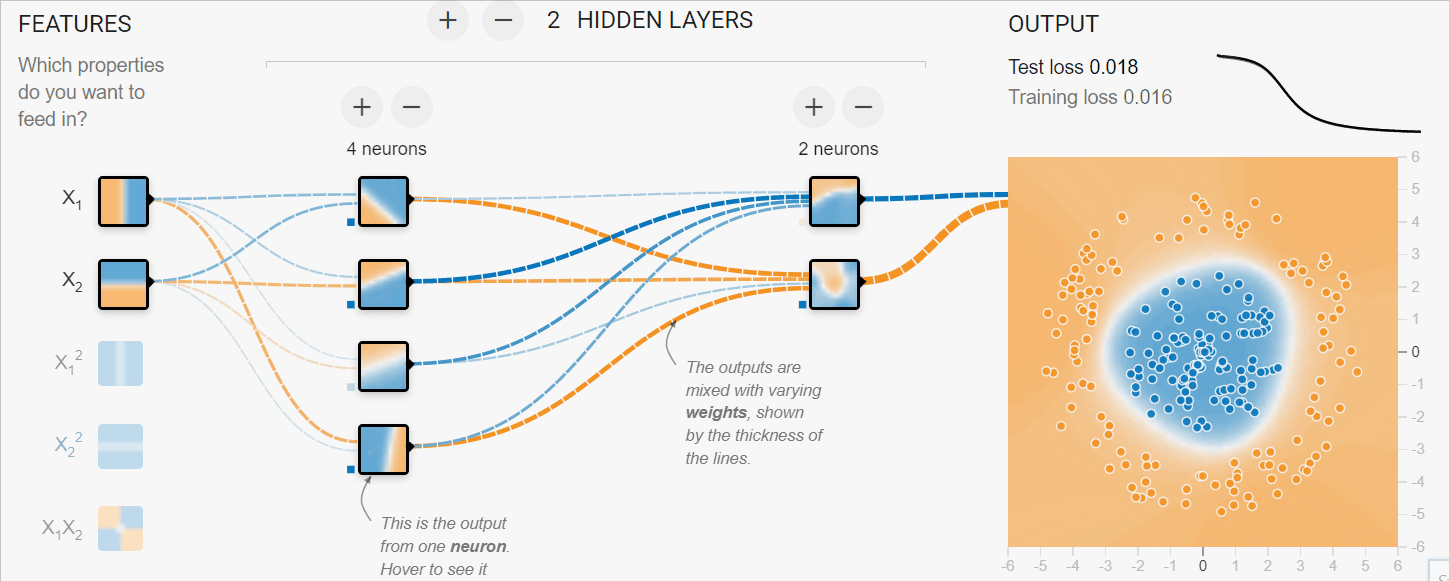
Imagen creada con TF Playground

Los algoritmos de aprendizaje profundo o redes neuronales profundas constan de múltiples capas y nodos ocultos. Por "profunda" se entiende la profundidad de las redes neuronales. Generalmente se utilizan para resolver problemas complejos como la clasificación de imágenes, el reconocimiento de voz y la generación de textos.

Aprende más sobre redes neuronales leyendo nuestro tutorial de aprendizaje profundo. Aprenderá cómo funcionan la función de activación, la función de pérdida y la retropropagación para producir resultados precisos. 

Tipos de redes neuronales

En las aplicaciones avanzadas de aprendizaje automático se utilizan múltiples tipos de redes neuronales. No tenemos un modelo de arquitectura que sirva para todos. El tipo más antiguo de red neuronal es el denominado perceptrón, creado por Frank Rosenblatt en 1958. 

En esta sección trataremos los 5 tipos de redes neuronales más utilizados en la industria tecnológica. 

Redes neuronales

Las redes neuronales feedforward constan de una capa de entrada, capas ocultas y una capa de salida. Se llama feedforward porque los datos fluyen en la dirección hacia adelante, y no hay retropropagación. Se utiliza sobre todo en clasificación, reconocimiento de voz, reconocimiento facial y reconocimiento de patrones.

Perceptrón multicapa

Los perceptrones multicapa (MLP) resuelven las deficiencias de las redes neuronales feedforward al no poder aprender mediante retropropagación. Es bidireccional y consta de múltiples capas ocultas y funciones de activación. Los MLP utilizan la propagación hacia delante para las entradas y la retropropagación para actualizar los pesos. Son redes neuronales básicas que han sentado las bases de la visión por ordenador, la tecnología del lenguaje y otras redes neuronales. 

Nota: Los MLP están formados por neuronas sigmoidales, no por perceptrones, porque los problemas del mundo real no son lineales.

Redes neuronales convolucionales (CNN)

Las redes neuronales de convolución (CNN) se utilizan generalmente en visión por ordenador, reconocimiento de imágenes y reconocimiento de patrones. Se utiliza para extraer características importantes de la imagen mediante múltiples capas convolucionales. La capa convolucional de la CNN utiliza una matriz (filtro) personalizada para convolucionar sobre las imágenes y crear un mapa. 

En general, las redes neuronales de convolución constan de una capa de entrada, una capa de convolución, una capa de agrupación, una capa totalmente conectada y una capa de salida. Lee nuestro tutorial sobre Redes Neuronales Convolucionales (CNN) en Python con TensorFlow para aprender más sobre cómo funcionan las CNN. 

Redes neuronales recurrentes (RNN)

Las redes neuronales recurrentes (RNN) se utilizan habitualmente para datos secuenciales como textos, secuencias de imágenes y series temporales. Son similares a las redes feed-forward, salvo que obtienen las entradas de secuencias anteriores mediante un bucle de realimentación. Las RNN se utilizan en PNL, predicciones de ventas y previsiones meteorológicas. 

Las RNN presentan problemas de gradiente evanescente, que se resuelven mediante versiones avanzadas de las RNN denominadas redes de memoria a corto plazo (LSTM) y redes de unidades recurrentes controladas (GRU). Lea el tutorial sobre redes neuronales recurrentes (RNN ) para obtener más información sobre las LSTM y las GRU. 

Implementación de redes neuronales en R

Aprenderemos a crear redes neuronales con los populares paquetes de R neuralnet y Keras. 

En el primer ejemplo, crearemos una red neuronal sencilla con el mínimo esfuerzo, y en el segundo, abordaremos un problema más avanzado utilizando el paquete Keras. 

Vamos a configurar el entorno R descargando las bibliotecas y dependencias esenciales. 

install.packages(c('neuralnet','keras','tensorflow'),dependencies = T)

Implementación sencilla de una red neuronal en R

En este primer ejemplo, utilizaremos los datos incorporados en R iris y resolveremos problemas de clasificación múltiple con una red neuronal sencilla. 

Empezaremos importando paquetes R esenciales para la manipulación de datos y la formación de modelos. 

library(tidyverse)
library(neuralnet)

Análisis de datos

Puede acceder a los datos escribiendo `iris` y ejecutándolo en la consola de R. Antes de entrenar los datos, tenemos que convertir los tipos de columnas de caracteres en factores.

Nota: estamos utilizando el espacio de trabajo DataCamp R para ejecutar los ejemplos. 

iris <- iris %>% mutate_if(is.character, as.factor)

La función `summary` se utiliza para el análisis estadístico y la distribución de datos. 

summary(iris)

Como vemos, tenemos datos equilibrados. Las tres clases objetivo tienen 50 muestras. 

Sepal.Length    Sepal.Width     Petal.Length    Petal.Width  
Min.   :4.300   Min.   :2.000   Min.   :1.000   Min.   :0.100 
1st Qu.:5.100   1st Qu.:2.800   1st Qu.:1.600   1st Qu.:0.300 
Median :5.800   Median :3.000   Median :4.350   Median :1.300 
Mean   :5.843   Mean   :3.057   Mean   :3.758   Mean   :1.199 
3rd Qu.:6.400   3rd Qu.:3.300   3rd Qu.:5.100   3rd Qu.:1.800 
Max.   :7.900   Max.   :4.400   Max.   :6.900   Max.   :2.500 
      Species 
setosa    :50 
versicolor:50 
virginica :50 

Formar y probar la división

Estableceremos semillas para la reproducibilidad y dividiremos los datos en conjuntos de datos de entrenamiento y de prueba para el entrenamiento y la evaluación del modelo. Lo dividiremos en 80:20. 

set.seed(245)
data_rows <- floor(0.80 * nrow(iris))
train_indices <- sample(c(1:nrow(iris)), data_rows)
train_data <- iris[train_indices,]
test_data <- iris[-train_indices,]

Entrenamiento de la red neuronal

El paquete neuralnet está anticuado, pero sigue siendo popular entre la comunidad R. 

La función `neuralnet` es sencilla. No nos ofrece la libertad de crear una arquitectura de modelos totalmente personalizable. 

En nuestro caso, le proporcionamos una fórmula de aprendizaje automático y datos, al igual que GLM. La fórmula consta de variables objetivo y características. 

Después, creamos dos capas ocultas, la primera capa con cuatro neuronas y la segunda con dos neuronas. 

model = neuralnet(
    Species~Sepal.Length+Sepal.Width+Petal.Length+Petal.Width,
data=train_data,
hidden=c(4,2),
linear.output = FALSE
)

Para visualizar la arquitectura de nuestro modelo, utilizaremos la función `plot`. Requiere un objeto modelo y el argumento `rep`. 

plot(model,rep = "best")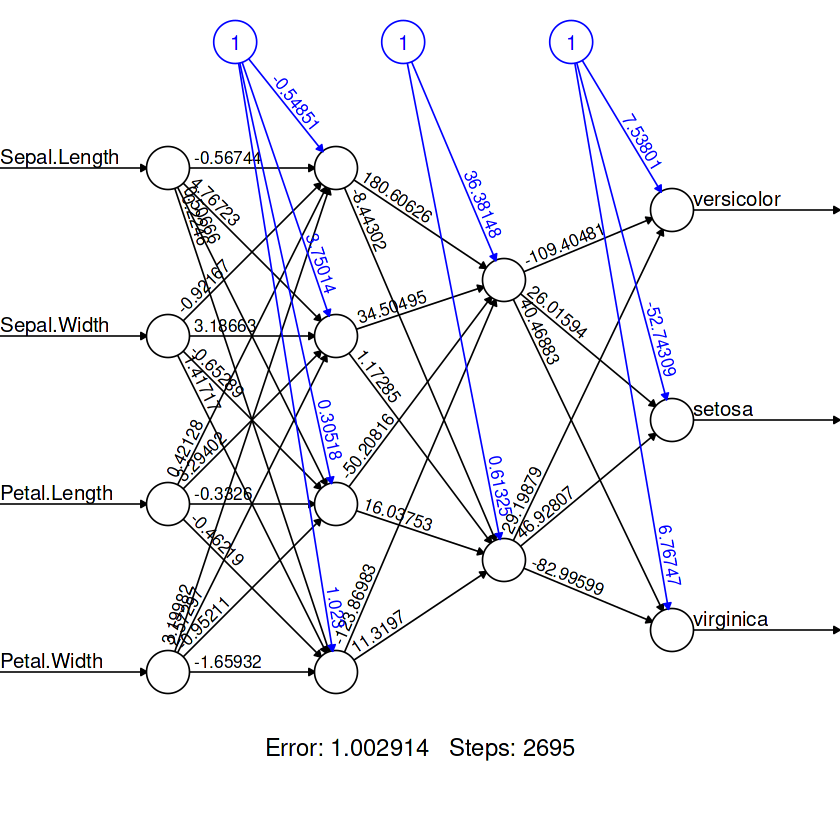

Evaluación de modelos

Para la matriz de confusión:

1. Predeciremos las categorías utilizando un conjunto de datos de prueba. 
2. Crear una lista de nombres de categorías.
3. Cree un marco de datos de predicción y sustituya las salidas numéricas por etiquetas. 
4. Utiliza tablas para mostrar los valores "reales" y "previstos" uno al lado del otro. 

pred <- predict(model, test_data)
labels <- c("setosa", "versicolor", "virginca")
prediction_label <- data.frame(max.col(pred)) %>%     
mutate(pred=labels[max.col.pred.]) %>%
select(2) %>%
unlist()

table(test_data$Species, prediction_label)

Obtuvimos resultados casi perfectos. Parece que nuestro modelo ha predicho erróneamente tres muestras. Podemos mejorar el resultado añadiendo más neuronas en cada capa. 

           prediction_label
            setosa versicolor virginica
  setosa          8          0        0
  versicolor      0         13        0
  virginica       0          3        6 

Para comprobar la precisión, primero tenemos que convertir los valores categóricos reales en numéricos y compararlos con los valores predichos. Como resultado, recibiremos una lista de valores booleanos. 

Podemos utilizar la función `sum` para hallar el número de valores `TRUE` y dividirlo por el número total de muestras para obtener la precisión. 

check = as.numeric(test_data$Species) == max.col(pred)
accuracy = (sum(check)/nrow(test_data))*100
print(accuracy)

El modelo ha predicho valores con una precisión del 90%. 

90

Nota: el código fuente de este ejemplo está disponible en el espacio de trabajo de R: Creación de modelos de redes neuronales (NN) en R.

Red neuronal convolucional en R con Keras

En este ejemplo, utilizaremos Keras y TensorFlow para construir y entrenar un modelo de Red Neuronal Convolucional para la tarea de clasificación de imágenes. Para ello, utilizaremos el conjunto de datos de imágenes cifar10, compuesto por 60.000 imágenes en color de 32x32 etiquetadas en diez categorías.

Imagen de CIFAR-10

Importar paquetes esenciales de R. 

library(keras)
library(tensorflow)

Preparación de los datos

Importaremos el conjunto de datos incorporado en Keras y lo dividiremos en conjuntos de entrenamiento y de prueba. 

c(c(x_train, y_train), c(x_test, y_test)) %<-% dataset_cifar10()

Divida las características de entrenamiento y prueba por 255 para normalizar los datos. 

x_train <- x_train / 255
x_test <-  x_test / 255

Construir el modelo

La API de Keras nos proporciona la flexibilidad necesaria para construir arquitecturas de redes neuronales complejas totalmente personalizables. 

En nuestro caso, crearemos varias capas de convolución, seguidas de la capa de agrupación máxima, la capa de abandono, la capa densa y la capa de salida. 

Estamos utilizando 'Leaky ReLU' como función de activación para todas las capas excepto la capa de salida. Para ello, utilizamos "softmax". 

Debemos ajustar la forma de entrada de la primera capa convolucional 2D a la forma de la imagen (32,32,3) del conjunto de datos de entrenamiento. 

model <- keras_model_sequential()%>%
  # Start with a hidden 2D convolutional layer
  layer_conv_2d(
    filter = 16, kernel_size = c(3,3), padding = "same",
    input_shape = c(32, 32, 3), activation = 'leaky_relu'
  ) %>%

  # 2nd hidden layer
  layer_conv_2d(filter = 32, kernel_size = c(3,3), activation = 'leaky_relu') %>%
 

  # Use max pooling
  layer_max_pooling_2d(pool_size = c(2,2)) %>%
  layer_dropout(0.25) %>%

  # 3rd and 4th hidden 2D convolutional layers
  layer_conv_2d(filter = 32, kernel_size = c(3,3), padding = "same", activation = 'leaky_relu') %>%

  layer_conv_2d(filter = 64, kernel_size = c(3,3), activation = 'leaky_relu') %>%

  # Use max pooling
  layer_max_pooling_2d(pool_size = c(2,2)) %>%
  layer_dropout(0.25) %>%
 
  # Flatten max filtered output into feature vector
  # and feed into dense layer
  layer_flatten() %>%
  layer_dense(256, activation = 'leaky_relu') %>%
  layer_dropout(0.5) %>%

  # Outputs from dense layer
  layer_dense(10, activation = 'softmax')

Para ver la arquitectura del modelo, utilizaremos la función `summary`. 

summary(model)

Tenemos dos capas convolucionales seguidas de una capa de agrupamiento máximo, dos capas convolucionales más, una capa de agrupamiento máximo, una capa aplanada para filtrar al máximo la salida en vectores y, a continuación, dos capas densas. 

Model: "sequential"
________________________________________________________________________________
Layer (type)                        Output Shape                    Param #    
================================================================================
conv2d_3 (Conv2D)                   (None, 32, 32, 16)              448        
________________________________________________________________________________
conv2d_2 (Conv2D)                   (None, 30, 30, 32)              4640       
________________________________________________________________________________
max_pooling2d_1 (MaxPooling2D)      (None, 15, 15, 32)              0          
________________________________________________________________________________
dropout_2 (Dropout)                 (None, 15, 15, 32)              0          
________________________________________________________________________________
conv2d_1 (Conv2D)                   (None, 15, 15, 32)              9248       
________________________________________________________________________________
conv2d (Conv2D)                     (None, 13, 13, 64)              18496      
________________________________________________________________________________
max_pooling2d (MaxPooling2D)        (None, 6, 6, 64)                0          
________________________________________________________________________________
dropout_1 (Dropout)                 (None, 6, 6, 64)                0          
________________________________________________________________________________
flatten (Flatten)                   (None, 2304)                    0          
________________________________________________________________________________
dense_1 (Dense)                     (None, 256)                     590080     
________________________________________________________________________________
dropout (Dropout)                   (None, 256)                     0          
________________________________________________________________________________
dense (Dense)                       (None, 10)                      2570       
================================================================================
Total params: 625,482
Trainable params: 625,482
Non-trainable params: 0
________________________________________________________________________________

Compilación del modelo

1. Estableceremos la tasa de aprendizaje utilizando la función de decaimiento exponencial programada. Reduce la tasa de aprendizaje después de 1500 pasos en 0,98.
2. Introduzca el objeto de tasa de aprendizaje en el optimizador Adamax.
3. Nuestra función de pérdida será la entropía cruzada categórica dispersa.
4. Compilar el modelo utilizando la función de pérdida y optimizador, y la métrica de rendimiento.

learning_rate <- learning_rate_schedule_exponential_decay(
  initial_learning_rate = 5e-3,
  decay_rate = 0.96,
  decay_steps = 1500,
  staircase = TRUE
)
opt <- optimizer_adamax(learning_rate = learning_rate)

loss <- loss_sparse_categorical_crossentropy(from_logits = TRUE)


model %>% compile(
  loss = loss,
  optimizer = opt,
  metrics = "accuracy"
)

Entrenamiento del modelo

Ajustaremos nuestro modelo y almacenaremos la métrica de evaluación en `history`. 

• Vamos a entrenar un modelo para 10 épocas y establecer el tamaño del lote a 32. 
• Añadir conjunto de datos de prueba para la validación.
• El argumento `shuffle` barajará los datos de entrenamiento al comienzo de cada época. 

history <- model %>% fit(
  x_train, y_train,
  batch_size = 32,
  epochs = 10,
  validation_data = list(x_test, y_test),
  shuffle = TRUE
)

Evaluación del modelo

Puede evaluar el modelo en un conjunto de datos de prueba mediante la función `evaluate`, que devolverá la pérdida final y la precisión. 

model %>% evaluate(x_test, y_test)

El reentrenamiento del modelo en 50 épocas mejorará la precisión del modelo. 

Loss 0.648191571235657 Accuracy 0.776799976825714

Para trazar gráficos de líneas de pérdida y precisión para cada época, utilizaremos la función `plot`. 

plot(history)

Si miramos el gráfico, podemos observar que la línea aún no se ha aplanado. Esto significa que con épocas más altas, podemos mejorar las métricas del modelo. 

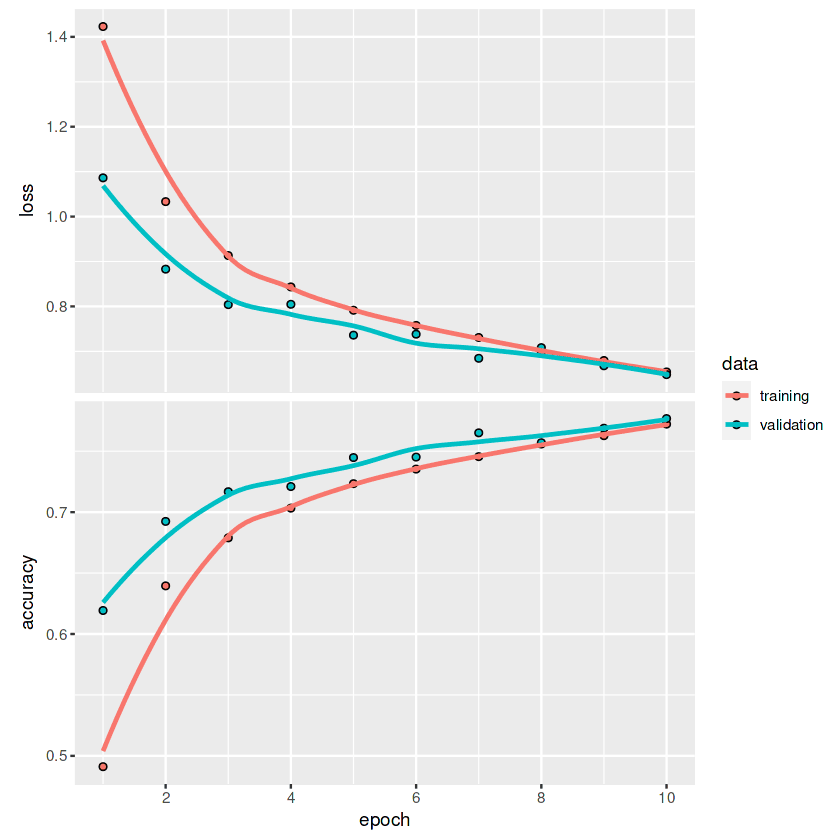
Si estás interesado en aprender más sobre la API Keras y cómo puedes utilizarla para construir redes neuronales profundas, consulta keras: Tutorial de aprendizaje profundo en R. 

Aplicaciones de las redes neuronales

Podemos encontrar ejemplos reales de redes neuronales en todas partes, desde aplicaciones móviles hasta ingeniería. Debido al reciente auge del lenguaje y los grandes modelos visuales, cada vez más empresas se interesan por implementar redes neuronales profundas para aumentar los beneficios y la satisfacción de los clientes. 

En esta sección, conoceremos las 10 principales aplicaciones de las redes neuronales que están dando forma al mundo moderno. 

1. Predicción tabular

Las redes neuronales simples son bastante eficaces con datos tabulares de gran tamaño. Podemos utilizarlos para problemas de clasificación, agrupación y regresión. 

2. Previsión del precio de las acciones

Muchas empresas utilizan LSTM, GRU y RNN para previsiones financieras. Les permite tomar mejores decisiones. 

3. Imagen médica

La detección del cáncer de mama, la detección de anomalías y la segmentación de imágenes son algunas de las aplicaciones de las redes neuronales convolucionales. Gracias a los transformadores preentrenados, hemos asistido a investigaciones avanzadas en materia de prevención de enfermedades y detección precoz de enfermedades mortales.  

4. E-commerce

Las recomendaciones de productos, las experiencias personalizadas y los chatbots son algunas de las aplicaciones de las redes neuronales utilizadas en el comercio electrónico. Estos modelos se utilizan principalmente para la agrupación, el procesamiento del lenguaje natural y la visión por ordenador con el fin de mejorar la experiencia de los clientes en la plataforma. 

5. Imagen generativa

Gracias a la popularidad de DALL-E 2 y a su difusión estable, este espacio se ha convertido en mainstream. Empresas como Canva y Adobe ya han implementado la capacidad de generar imágenes para aumentar el número de usuarios. Aparte del bombo y platillo, las imágenes generativas se utilizan en todos los sectores para crear datos sintéticos con el fin de mejorar el rendimiento, la estabilidad y los sesgos del modelo. 

6. Texto generativo

ChatGPT, GPT-3 y GPT-NEO son los modelos de redes neuronales profundas que dominan el espacio. Estos modelos se utilizan para ayuda a la programación, chatbots, traducción, preguntas/respuestas, etc. Está en todas partes y a las empresas les resulta fácil integrarla en sus sistemas actuales.

7. Bot de chat de atención al cliente

DailoGPT y Blenderbot son modelos conversacionales populares que mejoran tu experiencia de chatbot. Son adaptables y pueden ajustarse para un fin específico. En el futuro, no veremos largos tiempos de espera; estos chatbots serán capaces de entender sus problemas y ofrecer soluciones en tiempo real. 

8. Robótica

El aprendizaje por refuerzo y los modelos de redes neuronales de visión por ordenador están desempeñando un papel fundamental en las industrias de transferencia. Por ejemplo, gestión totalmente automatizada de almacenes, fábricas y experiencia de compra. 

9. Reconocimiento de voz

Los modelos de redes neuronales de reconocimiento del habla, conversión de texto a voz y detección de actividad de audio se utilizan para aplicaciones de asistencia al habla, transcripción automática y comunicaciones mejoradas. 

10. Multimodal

Text to Image (DALLE-2), Image Text, Visual Question Answering y extracciones de características son algunas de las aplicaciones utilizadas en las redes neuronales multimodales. En el futuro, verás texto a vídeo con audio. Podrás crear una película completa proporcionando el guión.

Conclusión

Los paquetes Keras y TensorFlow R nos proporcionan una gama completa de herramientas para crear una arquitectura de modelos compleja para tareas específicas. Puede cargar el conjunto de datos, realizar el preprocesamiento, construir y optimizar el modelo, y evaluar el modelo utilizando unas pocas líneas de código. Además, con Tensorflow, puedes monitorizar tus experimentos, configurar GPUs e implementar el modelo en producción. 

En este tutorial, hemos aprendido los fundamentos de las redes neuronales, el tipo de arquitectura del modelo y la aplicación. Además, hemos aprendido a entrenar una red neuronal simple con `neuralnet` y una red neuronal convolucional con `keras`. El tutorial abarca la construcción, compilación, entrenamiento y evaluación del modelo. 

Aprende más sobre Tensorflow y Keras API tomando el curso Introducción a TensorFlow en R. Aprenderá sobre tensorboard y otras API de TensorFlow, construirá redes neuronales profundas y mejorará el rendimiento del modelo utilizando regularización, abandono y optimización de hiperparámetros.