Guía completa para utilizar ANOVA en Excel

El análisis estadístico es fundamental para la toma de decisiones basada en datos en diversos campos, como la empresa, la sanidad, la educación y la investigación científica. Un método estadístico muy utilizado en entornos académicos y empresariales es el Análisis de la Varianza, o ANOVA.

Microsoft Excel proporciona una plataforma potente y fácil de usar para realizar ANOVA. Su interfaz intuitiva beneficia a los principiantes, eliminando la necesidad de software estadístico especializado como SPSS o SAS.

Esta guía simplificará el proceso de realizar ANOVA en Excel, proporcionando instrucciones claras y paso a paso que te ayudarán a realizar e interpretar con confianza las pruebas ANOVA. Tanto si eres estudiante, investigador o profesional que busca mejorar sus habilidades analíticas, esta guía te ayudará a aprender a aprovechar Excel para alguna de tus necesidades estadísticas habituales.

¿Qué es el ANOVA?

El ANOVA es un método estadístico utilizado para determinar si existen diferencias significativas entre las medias de tres o más grupos independientes. Son similares a otra prueba estadística llamada prueba t, que se utiliza para determinar si existe una diferencia significativa entre las medias de dos grupos. El ANOVA y las pruebas t representan dos de las muchas técnicas estadísticas que se tratan en nuestro completo curso de Análisis de Datos en Excel, que merece la pena visitar si te tomas en serio lo de llegar a dominar la estadística.

El ANOVA funciona comparando la varianza dentro de cada grupo con la varianza entre los grupos para evaluar si las medias de los grupos son iguales. Si la varianza entre grupos es significativamente mayor que la varianza dentro de los grupos, sugiere que al menos la media de un grupo difiere de las demás.

En términos generales, existen dos tipos de ANOVA:

• ANOVA unidireccional: Un ANOVA unidireccional examina el efecto de una única variable independiente sobre una variable dependiente comparando las medias de tres o más grupos.
• ANOVA de dos vías: Un ANOVA de dos vías evalúa el impacto de dos variables independientes simultáneamente y examina su interacción. 

Los investigadores académicos utilizan estas pruebas para analizar los resultados tras realizar un estudio controlado. Por ejemplo, los investigadores podrían utilizar el ANOVA para comparar la eficacia de distintos tratamientos o fármacos en varios grupos de pacientes. Las empresas con ánimo de lucro podrían utilizar el ANOVA para tomar decisiones basadas en datos, como comparar las puntuaciones de satisfacción de los clientes entre varios centros de servicio, o el rendimiento de las campañas publicitarias.

Por qué Microsoft Excel es bueno para el ANOVA

He aquí los pasos ordenados necesarios para realizar el ANOVA manualmente. Como referencia, el cociente f es el estadístico de prueba utilizado en el ANOVA para determinar si existen diferencias significativas entre las medias de los grupos. Implica múltiples cálculos para llegar a la estadística. 

1. Calcula la media global: Halla la media de todos los puntos de datos combinados.
2. Calcula las medias de grupo: Determina la media de cada grupo individual.
3. Calcula la Suma Total de Cuadrados: Mide la variación total de los datos sumando las diferencias al cuadrado entre cada punto de datos y la media general.
4. Calcula la suma de cuadrados entre grupos: Mide la variación entre las medias de los grupos y la media global.
5. Calcula la suma de cuadrados dentro de los grupos: Mide la variación dentro de cada grupo sumando las diferencias al cuadrado entre cada punto de datos y su media de grupo.
6. Calcula el cuadrado medio entre grupos: Divide la suma de cuadrados entre grupos por los grados de libertad entre grupos.
7. Calcula el cuadrado medio intragrupos: Divide la suma de cuadrados dentro de los grupos por los grados de libertad dentro de los grupos, donde los grados de libertad dentro de los grupos son el número total de observaciones menos el número de grupos.
8. Calcula el cociente F: Divide el cuadrado medio entre grupos por el cuadrado medio dentro de grupos para determinar el cociente f.

Como puedes ver, calcular el ANOVA manualmente es un poco complicado. Por esta razón, el software es el camino a seguir, y Microsoft Excel destaca por su amplio uso en la mayoría de las empresas y entornos académicos. 

Ten en cuenta también que, por lo general, los cálculos ANOVA forman parte de proyectos analíticos más amplios. Además de la potencia estadística de Excel, la disponibilidad de otras funciones, como las visualizaciones de beatuiful en Excel, añade peso al argumento de que Microsoft Excel es una gran herramienta para el ANOVA. 

Cómo activar el paquete de herramientas de análisis de datos en Excel

Los complementos en Excel son programas o funciones complementarias que pueden instalarse e integrarse con Excel para mejorar su funcionalidad. El ToolPak de Análisis de Datos es uno de esos complementos que ayuda con la mayoría de los requisitos de análisis de datos.

El complemento ToolPak de Análisis de Datos no está activado por defecto, por lo que tendrás que comprobar si ves el icono de Análisis de Datos en la esquina superior derecha, debajo de la pestaña Datos, como se muestra a continuación.

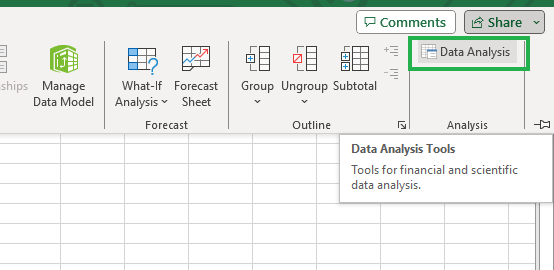
Paquete de herramientas de análisis de datos en Excel

Si no ves el Paquete de Herramientas de Análisis de Datos, puede significar que no está activado. Para activarlo, haz clic en Archivo en el menú y selecciona Opciones.

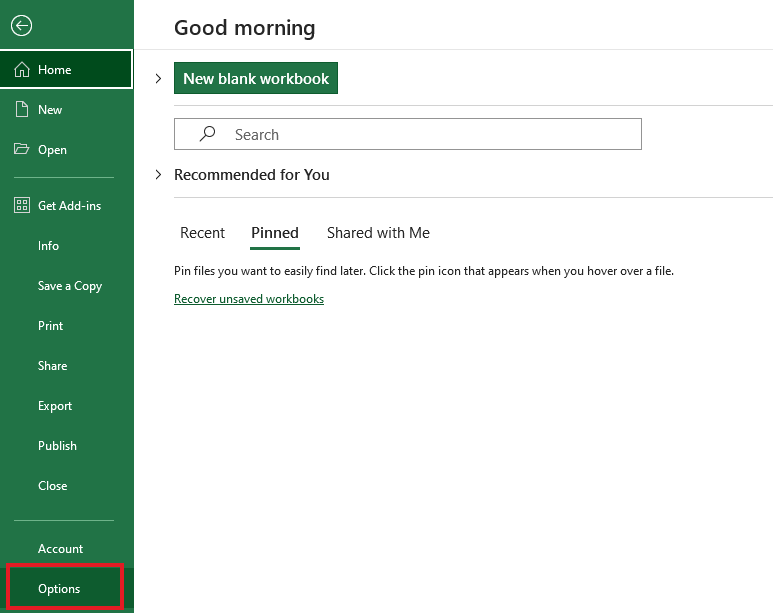Seleccionar opciones de la pestaña ArchivoSeleccionar opciones de la pestaña Archivo

Una vez abierto el cuadro de diálogo Opciones de Excel, selecciona Complementos.

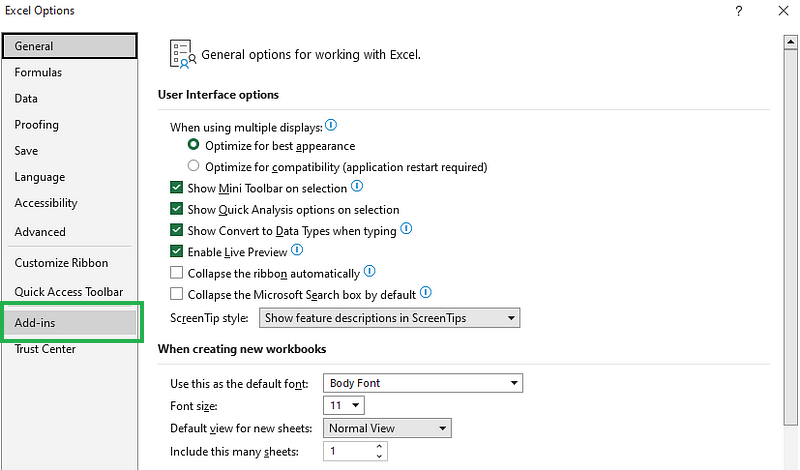el cuadro de diálogo Opciones de Excel.Selecciona Complementos en el cuadro de diálogo Opciones de Excel

A continuación, en el cuadro Gestionar de la parte inferior, selecciona Complementos de Excel y haz clic en Ir.

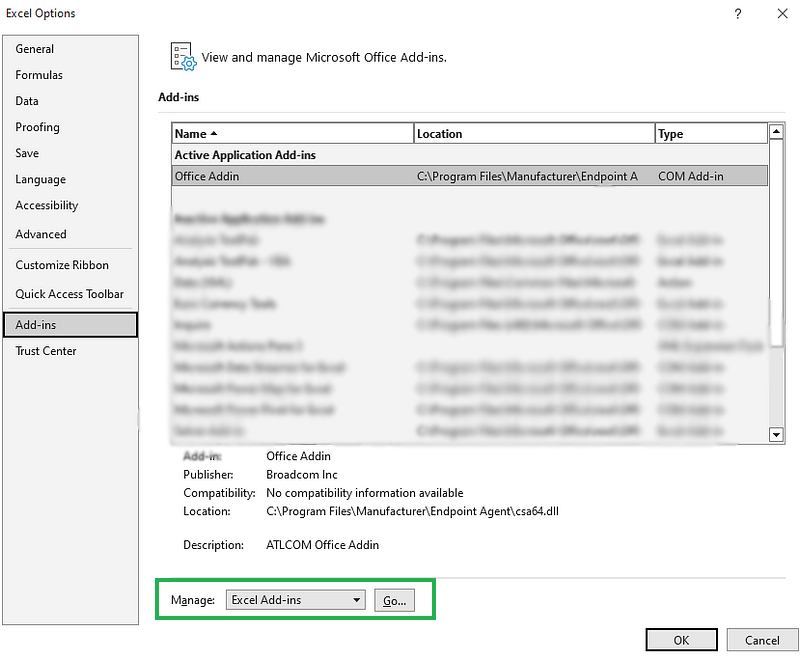Gestión de los complementos de ExcelGestión de los complementos de Excel

En el cuadro Complementos, marca Data Analysis ToolPak y haz clic en Aceptar.

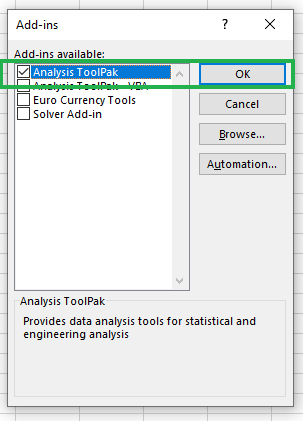
Habilitación del paquete de herramientas de análisis de datos

Ahora, cuando vuelvas a comprobarlo en la pestaña Datos, verás el nuevo icono Análisis de Datos. Ahora estamos preparados para aplicar el ANOVA en Excel utilizando algunos ejemplos.

ANOVA unidireccional en Excel: Un ejemplo práctico

Imagina que eres un analista de datos en una agencia de marketing al que se le ha encargado analizar el rendimiento de tres estrategias de marketing (A, B y C) sobre los ingresos por ventas.

Tu empresa quiere determinar si existe una diferencia significativa en los ingresos medios por ventas generados por estas estrategias. También has recopilado datos sobre los ingresos por ventas de cinco empresas diferentes de escala similar en la región A, donde se aplicó cada estrategia.

Los datos recogidos se han tabulado en la tabla siguiente:

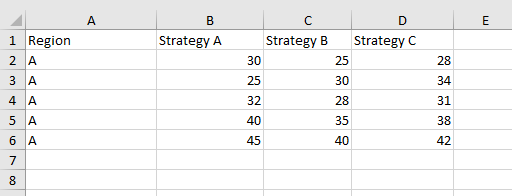
Datos para el ANOVA unidireccional

Utilicemos ahora el ANOVA para ver si hay una diferencia significativa entre las ventas medias de cada estrategia.

Como primer paso, selecciona las columnas B, C y D, incluida la primera fila como se muestra a continuación, y haz clic en el icono Análisis de Datos para abrir el complemento Toolpak de Análisis de Datos.

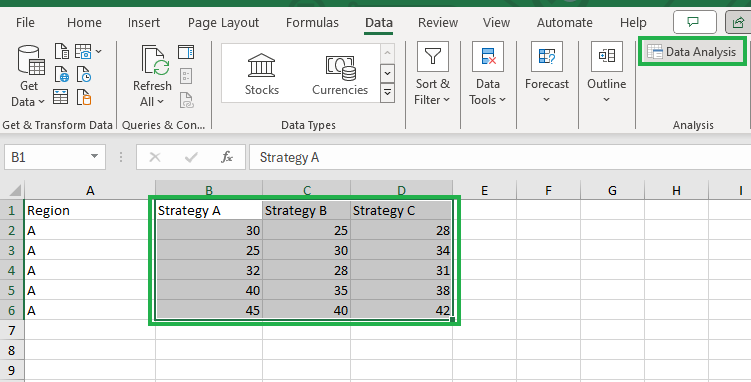Invocar el complemento ToolpakInvocar el complemento Data Analysis Toolpak

A continuación, selecciona Anova: Factor Único del cuadro de diálogo y haz clic en Aceptar.

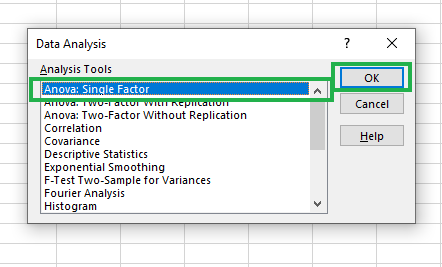
Seleccionar Anova: Opción de Factor Único

Aparecerá un cuadro de diálogo, como el que se muestra a continuación.

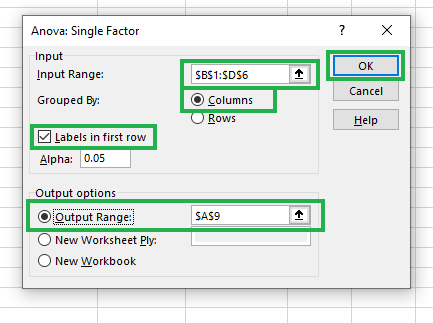
Detalles de relleno para Anova: Factor único

El Rango de entrada se rellena previamente, puesto que ya lo habíamos seleccionado antes de invocar el complemento. Selecciona Columnas para la opción Agrupado por, marca la casilla Etiquetas en la primera fila y deja los valores por defecto como están. Para el Rango de Salida, seleccionamos una celda de la misma hoja, digamos $A$9, o una nueva hoja de cálculo, como desees.

Haz clic en Aceptar y verás los resultados calculados en la misma hoja de Excel.

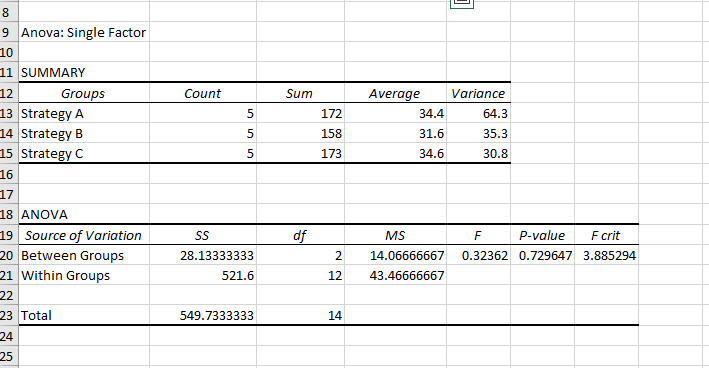Resultados del de una vía.Resultados del ANOVA de una vía

¡Has realizado con éxito un ANOVA unidireccional en tu conjunto de datos en un abrir y cerrar de ojos!

Prueba de hipótesis y ANOVA

Para comprender mejor los resultados, tenemos que profundizar en las pruebas de hipótesis y su conexión con el ANOVA. Las pruebas de hipótesis se tratan en detalle en nuestro curso de Introducción a la Estadística.

En las pruebas de hipótesis estadísticas, la hipótesis nula (H0) es una afirmación general que afirma que no existe relación entre dos fenómenos medidos. No postula ningún efecto ni ninguna diferencia. La hipótesis alternativa (H1 o Ha), en cambio, sugiere que las observaciones de la muestra están influidas por alguna causa no aleatoria, contradiciendo la hipótesis nula.

En nuestro ejemplo, para una prueba ANOVA unidireccional, las hipótesis serían:

• Hipótesis nula (H0): No hay diferencias en los ingresos medios por ventas generados por las tres estrategias.
• Hipótesis alternativa (Ha): Al menos una estrategia tiene una media de ingresos por ventas diferente.

El objetivo de la prueba ANOVA es comprobar estas hipótesis. Si el valor p es inferior al nivel de significación (normalmente 0,05), rechazamos la hipótesis nula a favor de la hipótesis alternativa.

Interpretación de los resultados del ANOVA unidireccional

Al leer la tabla ANOVA, vemos tres filas de resultados:

• Entre Grupos: Esta fila representa la variación entre las distintas estrategias de marketing y sus cálculos correspondientes.
• Dentro de los Grupos: Esta fila representa la variación dentro de cada estrategia de marketing y sus cálculos correspondientes.
• Total: Esta fila representa la variación total de los datos y los resultados relacionados.

El valor P es 0,73. Al ser mayor que el nivel de significación típico de 0,05, no rechazamos la hipótesis nula. En otras palabras, no hay pruebas suficientes para afirmar que exista una diferencia significativa entre las medias de las tres estrategias de marketing.

El valor del hematocrito F es 3,88. Sabemos que si el estadístico f (0,32) hubiera sido mayor que el valor crítico f, habríamos rechazado la hipótesis nula y concluido que existe una diferencia significativa entre las medias.

Según nuestra prueba ANOVA, parece que las tres estrategias de marketing no difieren significativamente en su eficacia. Sin embargo, es importante recordar que no rechazar la hipótesis nula no prueba que la hipótesis nula sea cierta. Sólo significa que no tenemos pruebas suficientemente sólidas para concluir lo contrario.

Veamos ahora cómo probar dos factores y su influencia en la variable dependiente.

ANOVA de dos vías en Excel: Un ejemplo práctico

Ampliemos nuestro ejemplo anterior para incluir un segundo factor. Esta vez, tu empresa quiere saber si hay diferencias significativas en los ingresos generados con distintas estrategias, y también si hay un efecto de interacción entre las estrategias y las regiones.

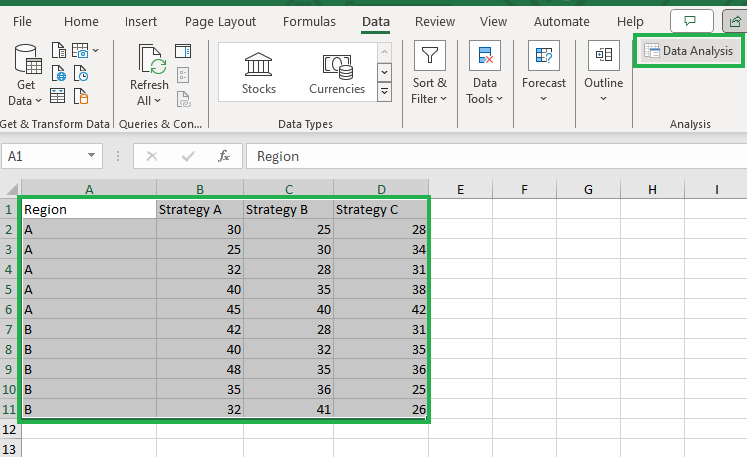
Los datos adicionales recogidos se han añadido a la hoja de cálculo, como se muestra a continuación:

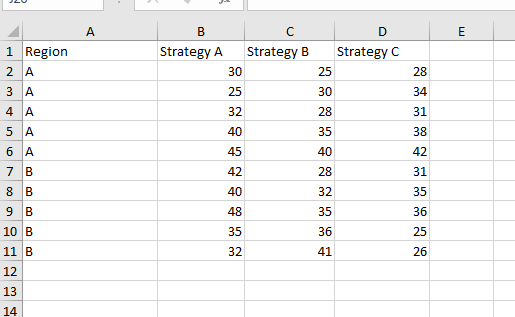
Datos para el ANOVA de dos vías

Como ahora hay dos factores -estrategia y región-, sabes que necesitamos un ANOVA de dos vías en lugar de un ANOVA de una vía.

Seleccionemos todo el rango de celdas y hagamos clic en el icono Análisis de Datos para invocar el complemento.

Invocar el complemento ToolpakInvocar el complemento Data Analysis Toolpak

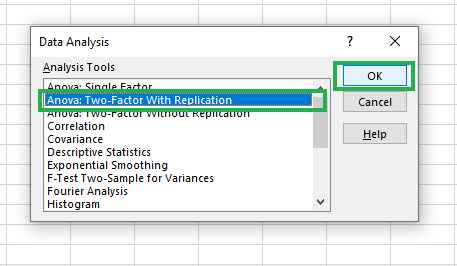
Se nos presenta un cuadro de diálogo con dos opciones diferentes para el ANOVA de dos vías.

Seleccionar Anova: Dos factores con opción de replicación

• ANOVA: Dos factores con replicación: Se utiliza cuando tenemos múltiples observaciones, o réplicas, para cada combinación de nuestros factores.
• ANOVA: Dos factores sin replicación: Se utiliza cuando sólo tenemos una observación para cada combinación de nuestros factores.

En nuestro caso, como tenemos múltiples observaciones para cada combinación de estrategia de marketing (A, B, C) y región (A, B), elegimos un ANOVA de dos factores con replicación.

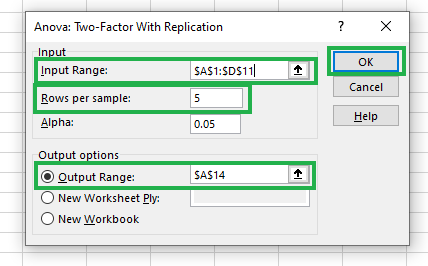
Tras hacer clic en Aceptar, verás el cuadro de diálogo que aparece a continuación con un rango de entrada previamente rellenado.

Detalles de relleno para Anova: Dos factores con replicación

En la opción Filas por muestra, introducimos 5 porque tenemos cinco puntos de datos para cada una de las regiones. Para el rango de salida, podemos seleccionar cualquier celda, por ejemplo $A$14, o una nueva hoja de cálculo, como desees. 

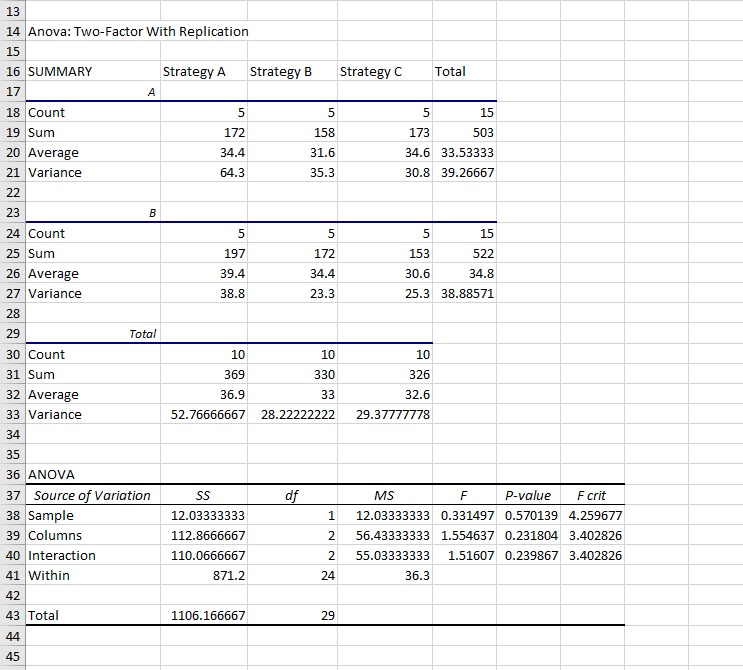Resultados del de dos vías.Resultados del ANOVA de dos vías

Eso es. Has realizado el ANOVA de dos vías para el conjunto de datos dado en unos pocos pasos.

Interpretación de los resultados del ANOVA bidireccional

Dediquemos un momento a comprender cómo leer la tabla ANOVA e identificar qué fila representa cada factor probado.

• Muestra: La fila Sample representa la variación entre las dos regiones.

• Columnas: La fila Columns representa la variación entre las distintas estrategias de marketing.

• Interacción: La fila Interaction representa el efecto de interacción entre las estrategias de marketing y las regiones.

• Dentro de: La fila Within representa la variación dentro de cada combinación de estrategia de marketing y región.

• Total: La fila Total representa la variación total de los datos.

Si el estadístico F es suficientemente grande, el valor p será suficientemente pequeño. Esto nos llevará a rechazar la hipótesis nula y a concluir que existen diferencias significativas entre las medias de los grupos.

Sin embargo, en nuestro caso, los estadísticos f de la muestra, las columnas y la interacción son menores que el valor crítico f de cada uno, y los valores p son todos mayores que 0,05. Por tanto, no rechazamos la hipótesis nula en los tres casos.

Esto significa que no hay pruebas suficientes para afirmar que existan diferencias significativas entre las medias de las regiones, las estrategias de marketing o un efecto de interacción entre las estrategias y las regiones.

Conclusión

El ANOVA es una importante herramienta estadística tanto en el ámbito académico como en el empresarial. Este tutorial presenta la técnica y sus dos tipos principales. Tomamos un ejemplo del mundo real e implementamos tanto el ANOVA unidireccional como el ANOVA bidireccional utilizando Microsoft Excel.

Además de la aplicación, también aprendimos a formular una hipótesis y a interpretar los resultados para aceptar o rechazar la hipótesis.

Para dominar Excel para tareas analíticas similares, el tema Fundamentos de Excel sería una buena apuesta, junto con la hoja de trucos de Excel para referencias rápidas.

¡Feliz aprendizaje!