Regresión lineal en Excel: Guía completa para principiantes

¿Qué es la regresión lineal?

La regresión lineal es una de las técnicas de aprendizaje automático más sencillas. Consiste en predecir el valor de una variable dependiente en función de una o varias variables independientes.

Por ejemplo, la regresión lineal puede aplicarse para predecir el precio de la vivienda en función de su tamaño o para predecir el peso de una persona en función de su altura. Los modelos de regresión lineal se clasifican principalmente en dos tipos: regresión lineal simple y múltiple.

• La regresión lineal simple se centra en modelizar la relación entre una variable dependiente y una variable independiente.
• La regresión lineal múltiple implica múltiples variables independientes para predecir la variable dependiente.

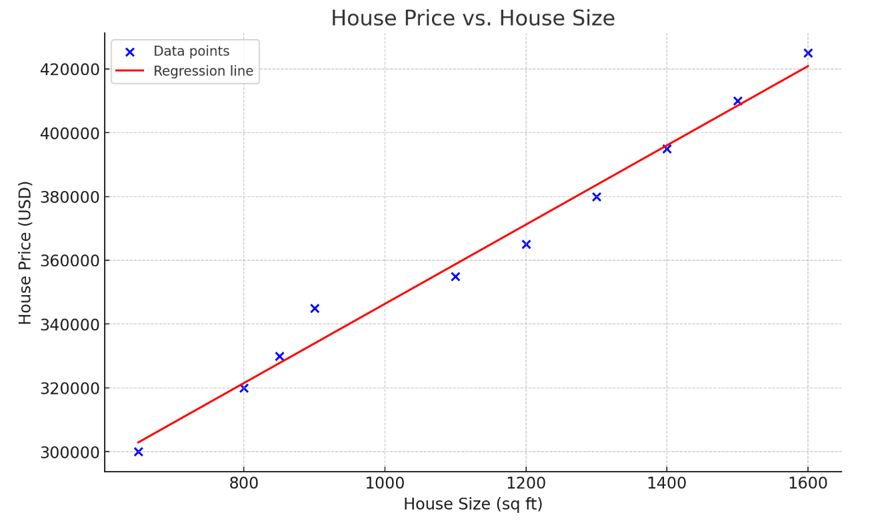
Imagen de OpenAI

El gráfico anterior representa una regresión lineal simple, que modela la relación entre el tamaño de la vivienda (variable independiente) y el precio de la vivienda (variable dependiente). Como se observa en la visualización, cuanto más grande es la casa, más cara es.

La ecuación de la recta de regresión es:

y = mx + c + ⍷

Si la fórmula anterior te resulta familiar, es porque probablemente has aprendido en la escuela que y = mx + c es la ecuación de una recta. En esta ecuación:

• Y es la variable dependiente
• X es la variable independiente
• M es la pendiente, que cuantifica el cambio en la variable dependiente para un cambio de una unidad en la variable independiente.
• C es la intersección y, que representa el valor de y cuando x es 0.

⍷ representa el término residual o de error. Es la diferencia entre el valor real y el valor predicho por el valor de regresión. distingue una recta de regresión de una recta puramente determinista, haciendo que la relación entre x e y no sea perfectamente predecible.

Para una guía más extensa sobre el tema, lee nuestro artículo que explica los fundamentos de la regresión lineal.

¿Por qué Excel para la regresión lineal?

He aquí algunos factores que hacen de Excel una herramienta eficaz para realizar la regresión lineal:

1. Plataforma unificada

En 2024, Excel es utilizado por más de 731.000 empresas en Estados Unidos e innumerables más en todo el mundo, según informa Statista. Los ejecutivos de todos los niveles organizativos utilizan Excel para la gestión de datos y la elaboración de informes.

Al crear modelos predictivos como la regresión lineal en Excel, las empresas pueden consolidar sus actividades de elaboración de informes y modelos predictivos en una única plataforma. Esto permite a las organizaciones agilizar los flujos de trabajo en lugar de tener que cambiar constantemente entre entornos de programación y hojas de cálculo Excel.

2. Facilidad de uso

Si eres principiante en el sector de los datos, la mera idea de crear un modelo predictivo puede parecer intimidante debido a la codificación que implica. Excel simplifica este proceso, permitiéndote trabajar en una interfaz con la que ya estás familiarizado. Con Excel, construir un modelo de regresión lineal se convierte en un proceso sencillo, realizable en unos pocos clics.

3. Informes y visualización

Excel ofrece una gran capacidad de visualización, que te permite representar gráficamente la relación entre distintas variables para comprenderlas mejor. Además, simplifica la creación de informes, garantizando que las visualizaciones puedan incrustarse fácilmente en presentaciones de PowerPoint para una comunicación eficaz con las partes interesadas.

Cómo aplicar la regresión lineal en Excel

Antes de sumergirte en este tutorial, descarga el conjunto de datos disponible en este repositorio de GitHub. Este conjunto de datos ha sido creado específicamente por OpenAI con fines educativos. Dominar las operaciones básicas de una hoja de cálculo, como introducir datos, aplicar fórmulas sencillas y navegar por las hojas de cálculo, mejorará tu capacidad para seguir este tutorial.

Paso 1: Paquete de herramientas de análisis de datos en Excel

En primer lugar, tenemos que activar el Paquete de Herramientas de Análisis de Datos en Excel. Se trata de un programa complementario de Excel que proporciona diversas herramientas de análisis de datos, incluida la que utilizaremos para la regresión lineal.

Para ello, primero, abre el archivo Excel y ve a Archivo -> Opciones. En el cuadro de diálogo Opciones, selecciona Complementos -> Complementos de Excel y haz clic en Ir:

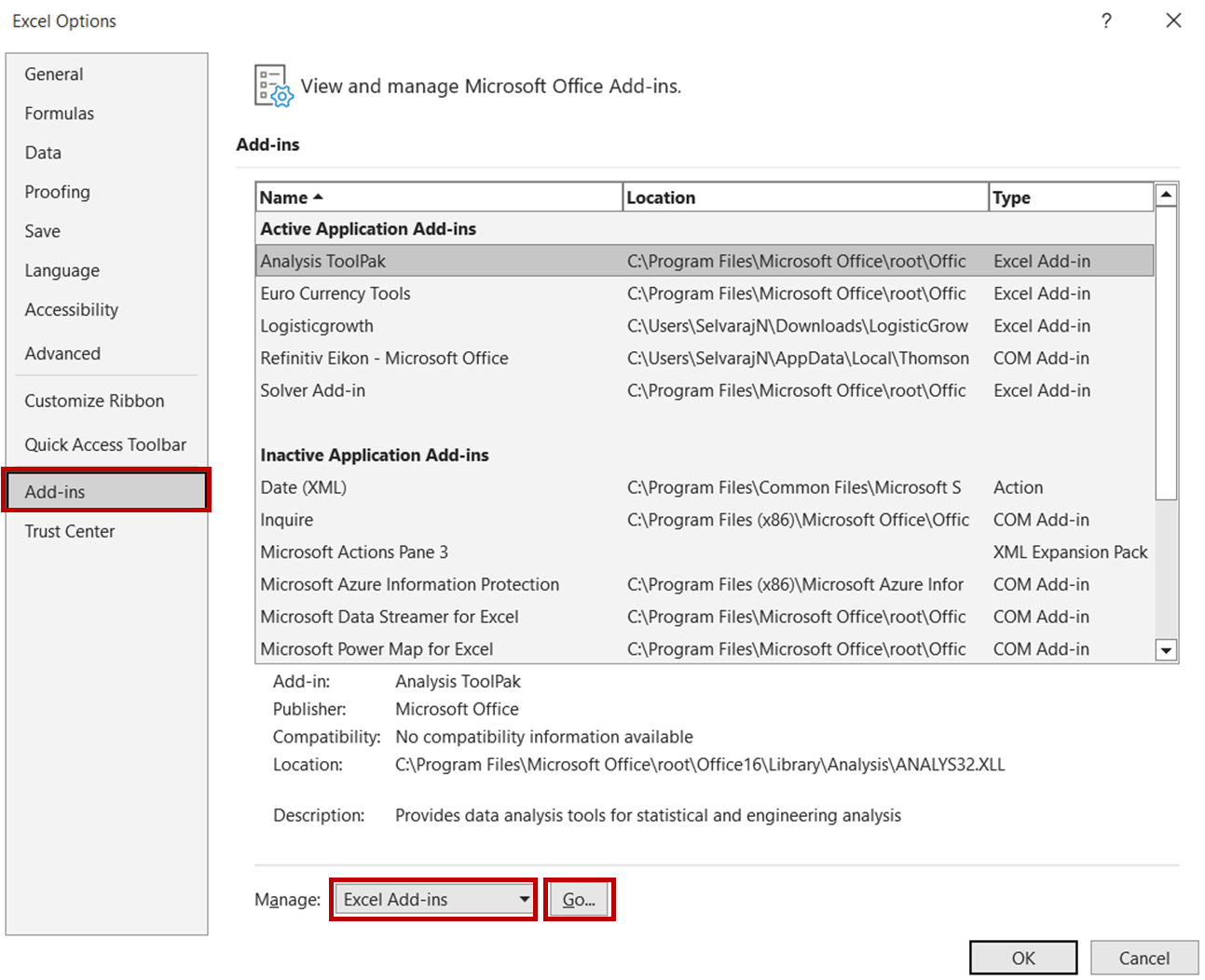
En el cuadro de diálogo Complementos, marca la opción Analysis ToolPak y haz clic en Aceptar.

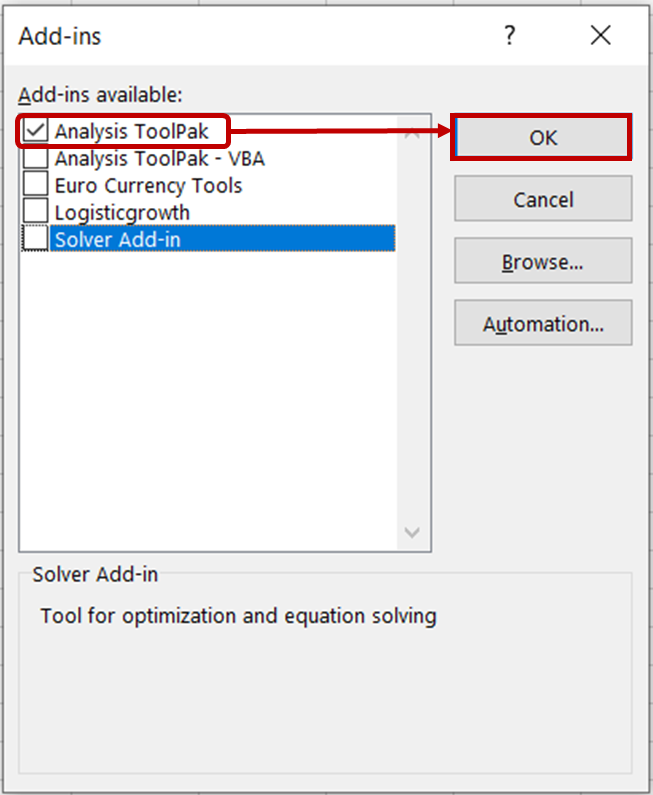
Ahora deberías ver las herramientas de Análisis de Datos en la pestaña Datos.

Paso 2: Cómo realizar una regresión lineal en Excel

Ahora que hemos activado el Paquete de Herramientas de Análisis de Datos, podemos proceder a realizar una regresión lineal sobre el conjunto de datos. Abre el conjunto de datos de ventas de helados y ve a la pestaña Datos. En el grupo Análisis, haz clic en Análisis de datos.

A continuación, selecciona Regresión en la lista de herramientas de análisis y haz clic en Aceptar.

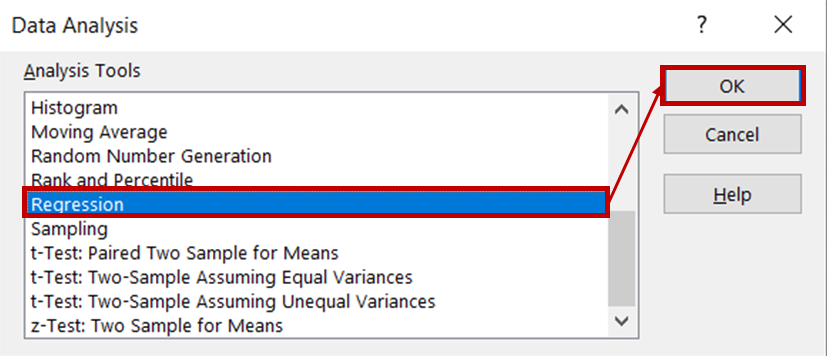
En el cuadro de diálogo de regresión, para el Rango Y de entrada, selecciona la columna que contiene los datos de ventas de helados. Para el rango Entrada X, selecciona las columnas que contienen los datos de temperatura y precio. Asegúrate de que la casilla Etiquetas está marcada, ya que esto ayudará a Excel a reconocer las cabeceras y a tratar las filas restantes como datos numéricos. En la sección Opciones de salida , selecciona Nueva hoja de cálculo Ply para ver los resultados en una nueva hoja de cálculo.

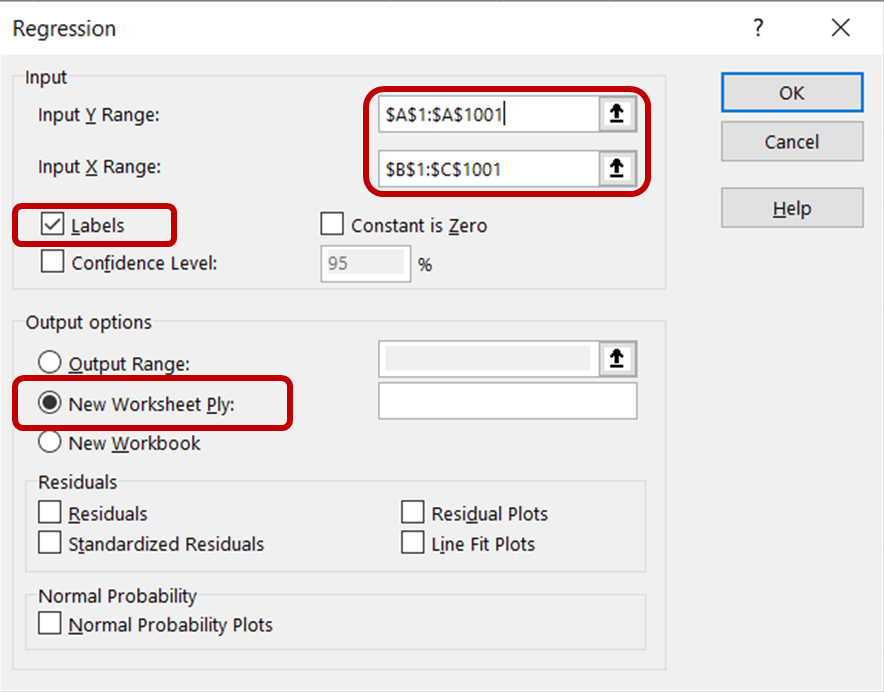
A continuación, haz clic en Aceptar para ejecutar el análisis de regresión en el conjunto de datos.

Paso 3: Interpretación de los resultados

Después de realizar la regresión, deberías ver que aparece automáticamente una nueva hoja de cálculo dentro del archivo de Excel, mostrando una serie de tablas de resultados con el siguiente aspecto:

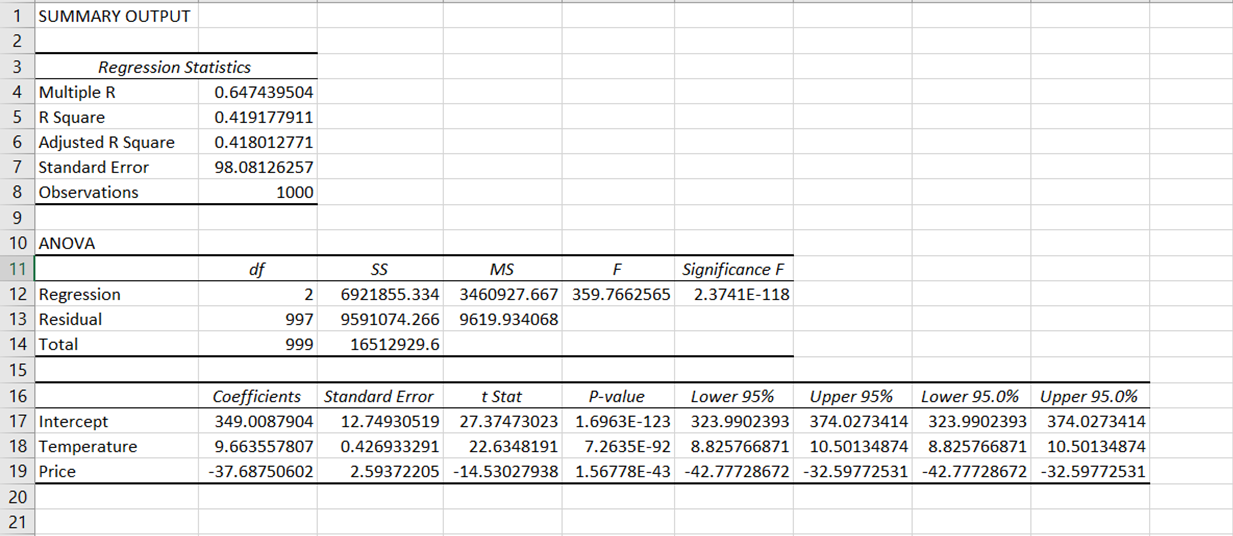
Los resultados de la salida de la regresión se han desglosado en varios componentes: estadística de la regresión, ANOVA, coeficientes, error estándar, estadística t, valor P e intervalo de confianza.

Examinemos cada uno de estos componentes con más detalle:

1. Resumen estadístico

Excel informa de las siguientes estadísticas de resumen como resultado del análisis de regresión:

Multiple R

Es un coeficiente de correlación que mide la fuerza y la dirección de una relación lineal entre variables. Va de -1 a 1, con valores cercanos a -1 o 1 que indican una fuerte relación y valores cercanos a 0 que sugieren que no hay correlación.

En nuestro análisis, el coeficiente de correlación es de aproximadamente 0,65, lo que muestra una correlación positiva moderada entre nuestra variable dependiente (ventas de helados) y las variables independientes (precio y temperatura).

Cuadrado R

^R2 es una medida estadística que nos indica lo bien que se ajustan los datos al modelo de regresión. Es el cuadrado del coeficiente de correlación, R múltiple, y representa la proporción de varianza de la variable dependiente que pueden explicar las variables independientes.

^R2 oscila entre 0 y 1, y los valores más próximos a 1 sugieren un mejor ajuste del modelo. Nuestro^R2 es de aproximadamente 0,419, lo que significa que el modelo puede explicar alrededor del 41,9% de la varianza de las ventas de helados.

R cuadrado ajustado

Es el valor R-cuadrado ajustado al número de predictores del modelo. Suele ser una medida mejor cuando se comparan modelos con distinto número de predictores. En nuestro caso, el^R2 ajustado es de 0,418. Esto es muy similar a nuestro^R2, lo que sugiere que las variables independientes que hemos incluido (temperatura y precio) son relevantes para el modelo y no han introducido una gran penalización.

Error estándar

El error típico mide la distancia media a la que los valores observados se alejan de la recta de regresión. Un error típico menor es mejor, ya que significa que la recta de regresión se ajusta mejor a los datos.

En nuestro caso, el error típico es de aproximadamente 98,05, lo que indica que los valores reales de ventas de helados se desvían de los predichos en unas 98,05 unidades.

Observaciones

Se refiere al número total de puntos de datos (filas) analizados en el conjunto de datos, excluyendo las cabeceras.

2. ANOVA (Análisis de la Varianza)

ANOVA significa Análisis de la Varianza. Es una técnica estadística que proporciona información sobre el nivel de variabilidad dentro de un modelo de regresión mediante:

Grados de libertad (df)

Representa el número de valores del cálculo final que pueden variar libremente. En el contexto del ANOVA, "Regresión" df se refiere al número de variables independientes del modelo, que es 2. La df "residual" se calcula restando el número de variables independientes y 1 del número total de observaciones. En nuestro caso, es 997.

Suma de cuadrados (SS)

Esto cuantifica la variación. El "SS de regresión" mide la variación de la variable dependiente que puede explicar el modelo. "SS residual" representa la variación no explicada.

Cuadrado medio (CM)

Se obtiene dividiendo la Suma de Cuadrados (SS) por los Grados de Libertad (df).

Estadístico F (F)

Esta estadística determina la significación global del modelo. Un valor F más alto indica que el modelo se ajusta mejor a los datos.

Significado F

Es el valor P asociado al estadístico F. Un valor p muy pequeño (inferior a 0,05) indica que tu modelo se ajusta mejor a los datos que un modelo sin variables independientes. En nuestro caso, el valor F de Significación es inferior a 0,05, lo que indica que el modelo se ajusta bien a los datos.

3. Coeficientes

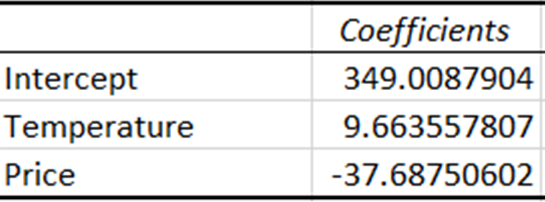
Los coeficientes representan la cantidad estimada de cambio en la variable dependiente para un cambio de una unidad en la variable independiente.

El coeficiente para la temperatura indica que con cada aumento de una unidad en la temperatura, las ventas aumentan alrededor de 9,66 unidades. Por el contrario, el coeficiente del precio indica que las ventas disminuyen aproximadamente 37,69 unidades con un aumento de una unidad en el precio.

4. Error estándar

El error típico mide la distancia media entre los valores observados y la recta de regresión. Un error típico más bajo indica un modelo mejor.

5. t Declaración

El estadístico t es el coeficiente dividido por su error típico. Un estadístico t mayor indica que el coeficiente es distinto de cero, lo que implica que tiene un mayor impacto en la variable dependiente.

6. Valor P

Los valores P nos indican la probabilidad de observar un estadístico t tan extremo como el observado en el supuesto de que la hipótesis nula sea cierta (es decir, que el coeficiente de una variable independiente sea 0).

En términos sencillos, cuanto mayor sea el estadístico t y menor el valor P, mayor será la evidencia contra la hipótesis nula, apoyando la conclusión de que las variables independientes (precio y temperatura) tienen un impacto estadísticamente significativo en la variable dependiente (ventas de helados).

7. Intervalos de confianza (95% inferior y 95% superior)

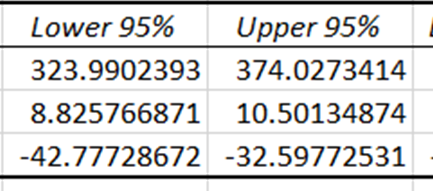
Los intervalos de confianza proporcionan los límites inferior y superior dentro de los cuales se espera que se sitúen los coeficientes verdaderos de las variables independientes, con un nivel de confianza del 95%. Dado que los intervalos de confianza para el precio y la temperatura son distintos de cero, estos coeficientes tienen un impacto estadísticamente significativo en la predicción de las ventas de helados.

Cómo visualizar una regresión lineal en Excel

Visualizar la relación entre dos variables puede mejorar mucho tu comprensión del conjunto de datos. Aunque el paquete de herramientas de análisis de Excel proporciona estadísticas resumidas detalladas, una representación gráfica puede mostrarte al instante la fuerza y la dirección de una relación entre variables.

Crear un gráfico de dispersión con una línea de tendencia es una forma eficaz de visualizar esta relación, y puede hacerse en menos de cinco minutos. Esta técnica de visualización te permite ver de un vistazo cómo influye una variable en otra.

He aquí cómo visualizar la relación entre "Ventas de helados" y "Temperatura":

1. Insertar un gráfico de dispersión

Primero, resalta las celdas que contienen las variables "Ventas de helado" y "Temperatura". A continuación, ve a la pestaña "Insertar" y haz clic en el icono del gráfico de "Dispersión":

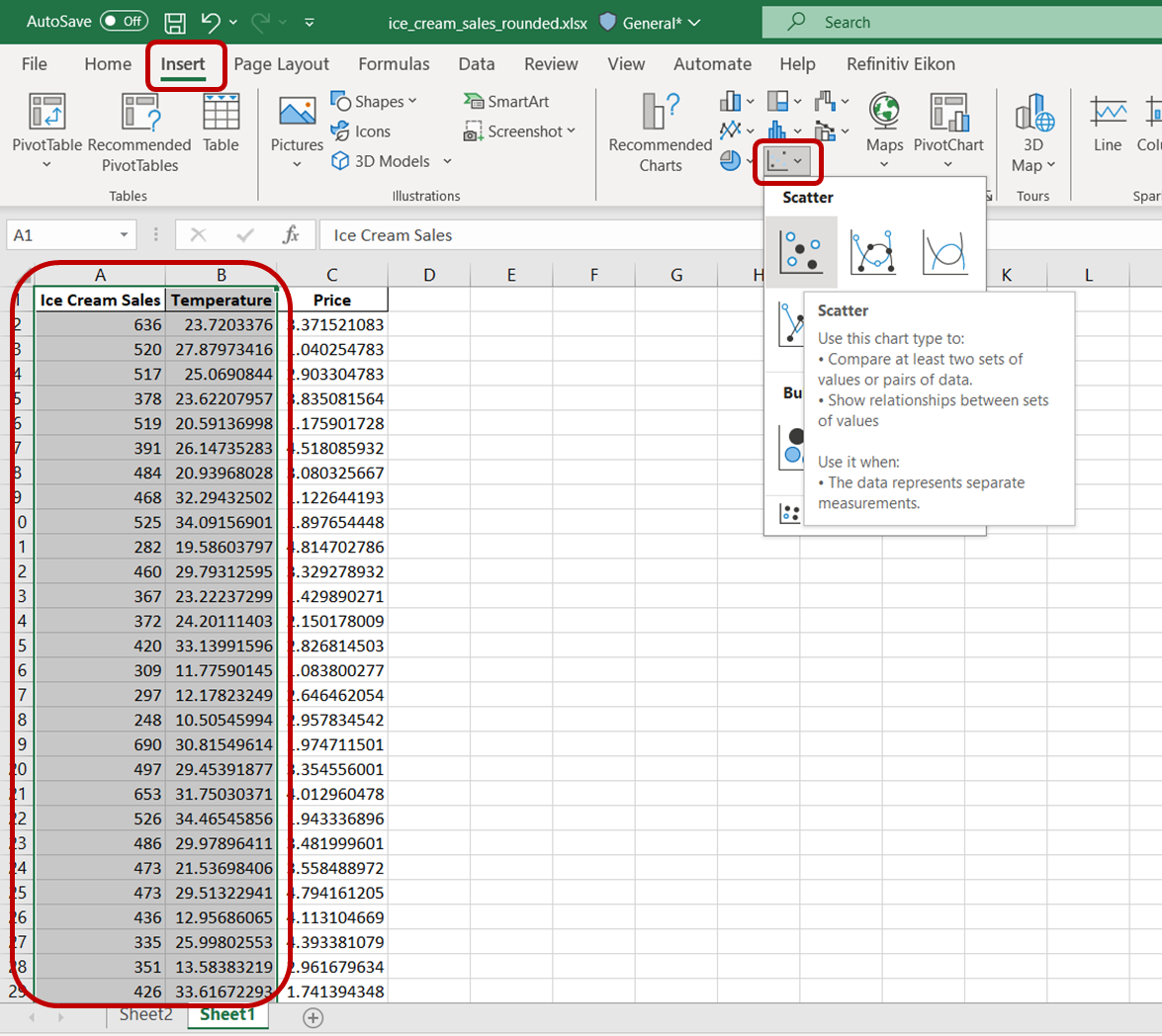
Verás un gráfico de dispersión simple con este aspecto:

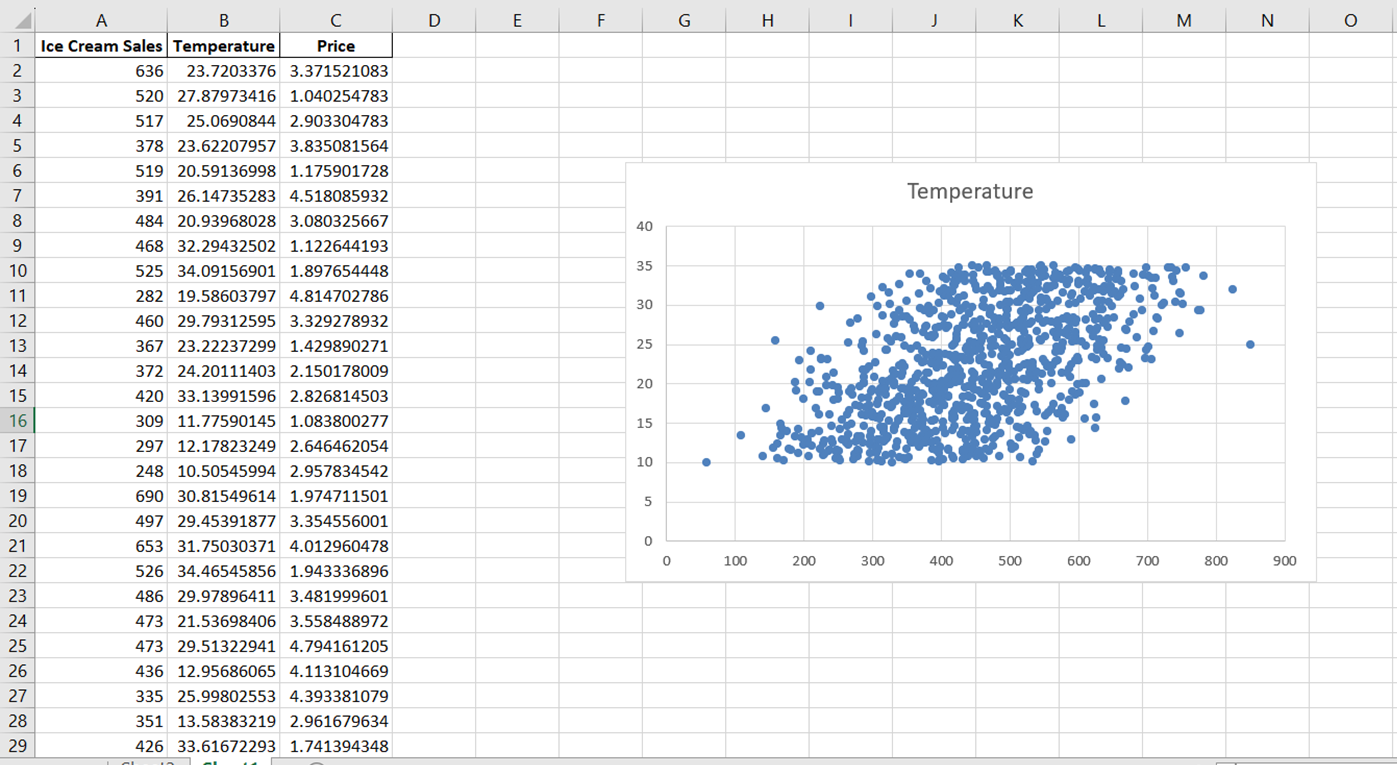
2. Reetiquetar el Gráfico y los Ejes

Cambiemos ahora el nombre del gráfico para describir con precisión la relación que estamos visualizando. Simplemente haz clic en el título del gráfico y cámbialo por "Relación entre las ventas de helados y la temperatura".

A continuación, para cambiar la etiqueta del eje x, ve a "Diseño del gráfico". En el desplegable "Añadir elemento del gráfico", selecciona "Títulos de los ejes" -> "Horizontal primario":

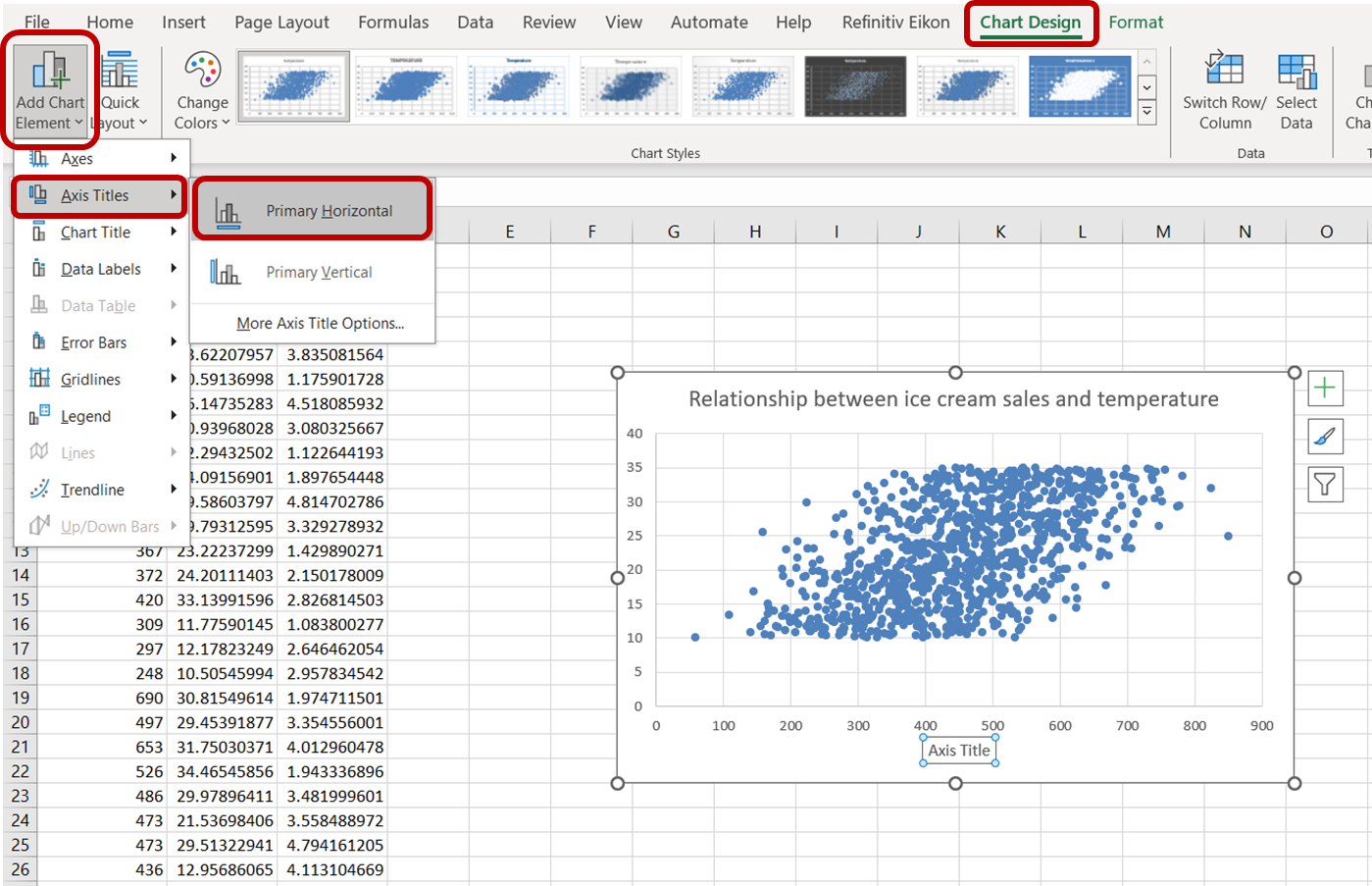
Haz clic en el título del eje por defecto que aparece y escribe "Ventas de helados" para etiquetar con precisión el eje. Haz lo mismo para el eje y seleccionando "Vertical Primario" y sustituyendo el título del eje por "Temperatura:"

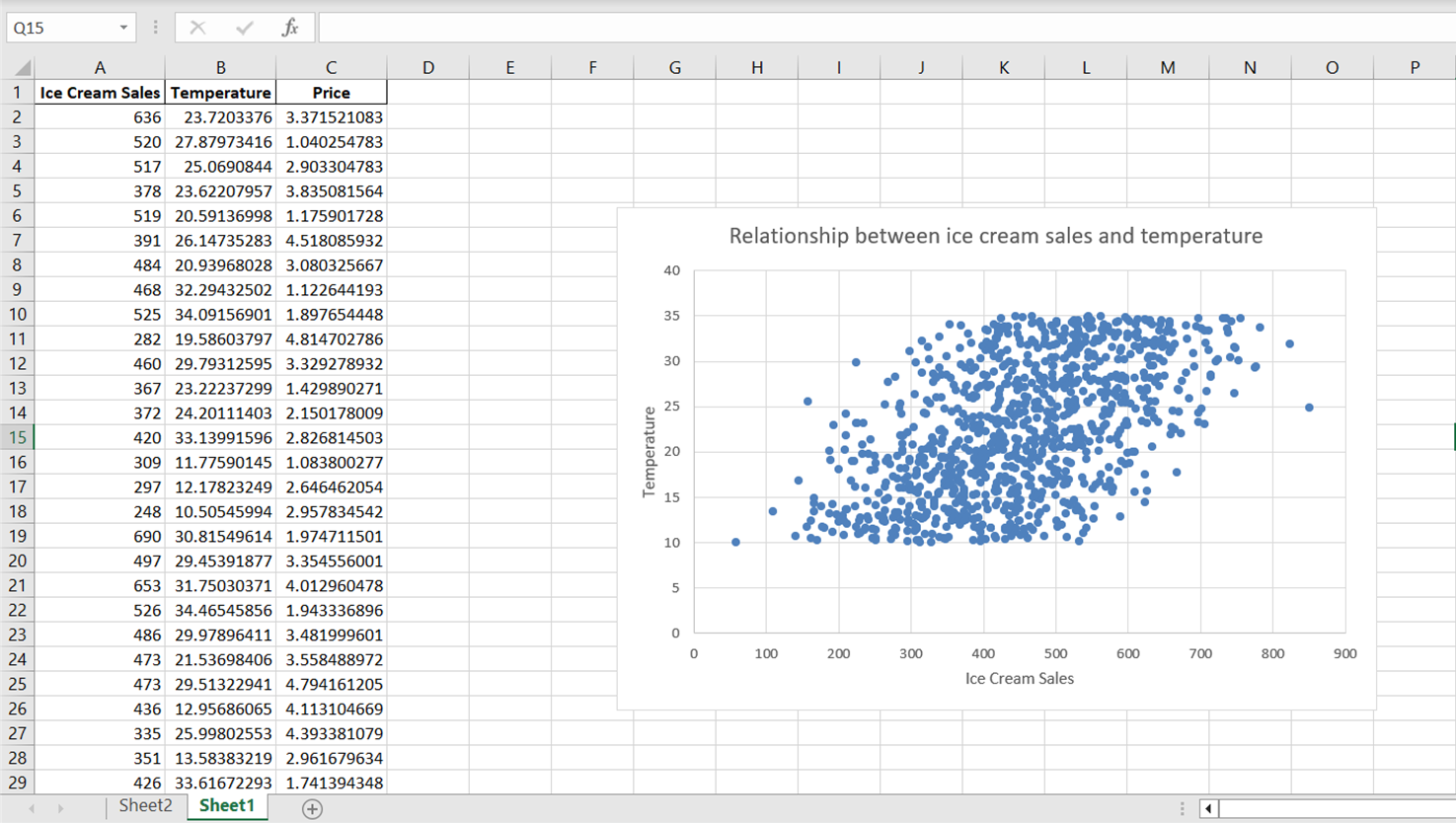
3. Añadir una línea de tendencia

Observa que, aunque el diagrama de dispersión revela una dirección general en la relación entre la temperatura y las ventas de helados, los puntos de datos parecen estar muy dispersos. Para resumir mejor esta relación, incluyendo su dirección general y su pendiente, incorporemos una línea de tendencia o una línea de mejor ajuste.

Para añadir una línea de tendencia a este gráfico, simplemente haz clic en cualquier punto de datos de este gráfico de dispersión. Esta acción seleccionará todos los puntos de datos del gráfico. A continuación, haz clic con el botón derecho del ratón en los puntos de datos seleccionados. En el menú que aparece, elige "Añadir línea de tendencia:"

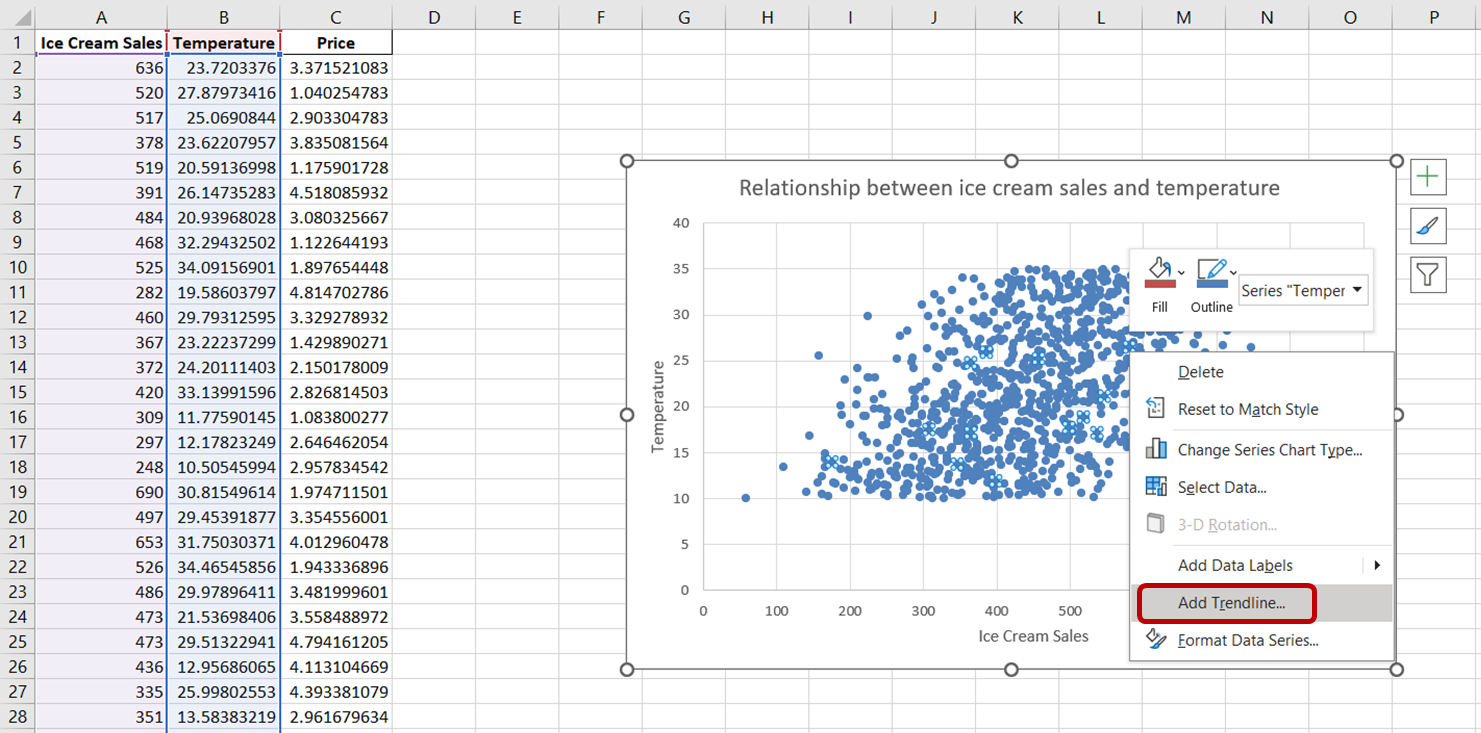
Deberías ver aparecer una línea de puntos en el gráfico, que ilustra la dirección general de la relación entre las variables:

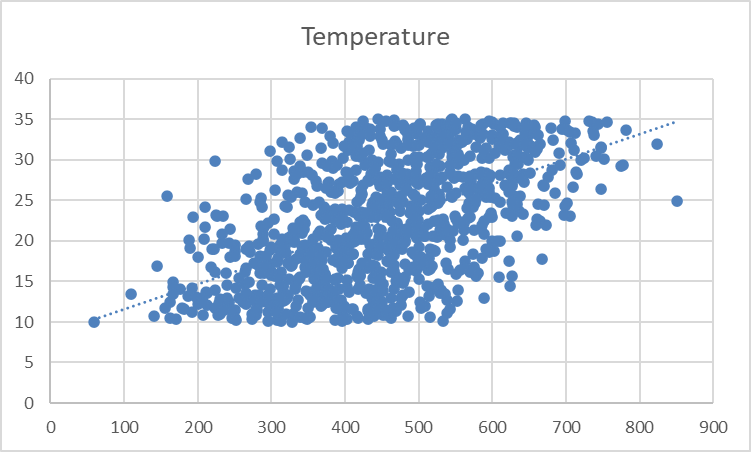
4. Formatear la línea de tendencia

La línea de tendencia parece tenue y sutil. Vamos a ajustar su formato para que sea más visible.

Primero, haz clic en la línea de tendencia para seleccionarla. Aparecerá el panel de tareas "Formatear línea de tendencia" en la parte derecha de tu ventana de Excel. En este panel de tareas, selecciona la opción "Relleno y Línea". A continuación, aumenta la anchura de la línea de tendencia a 3pt y cambia su color a rojo:

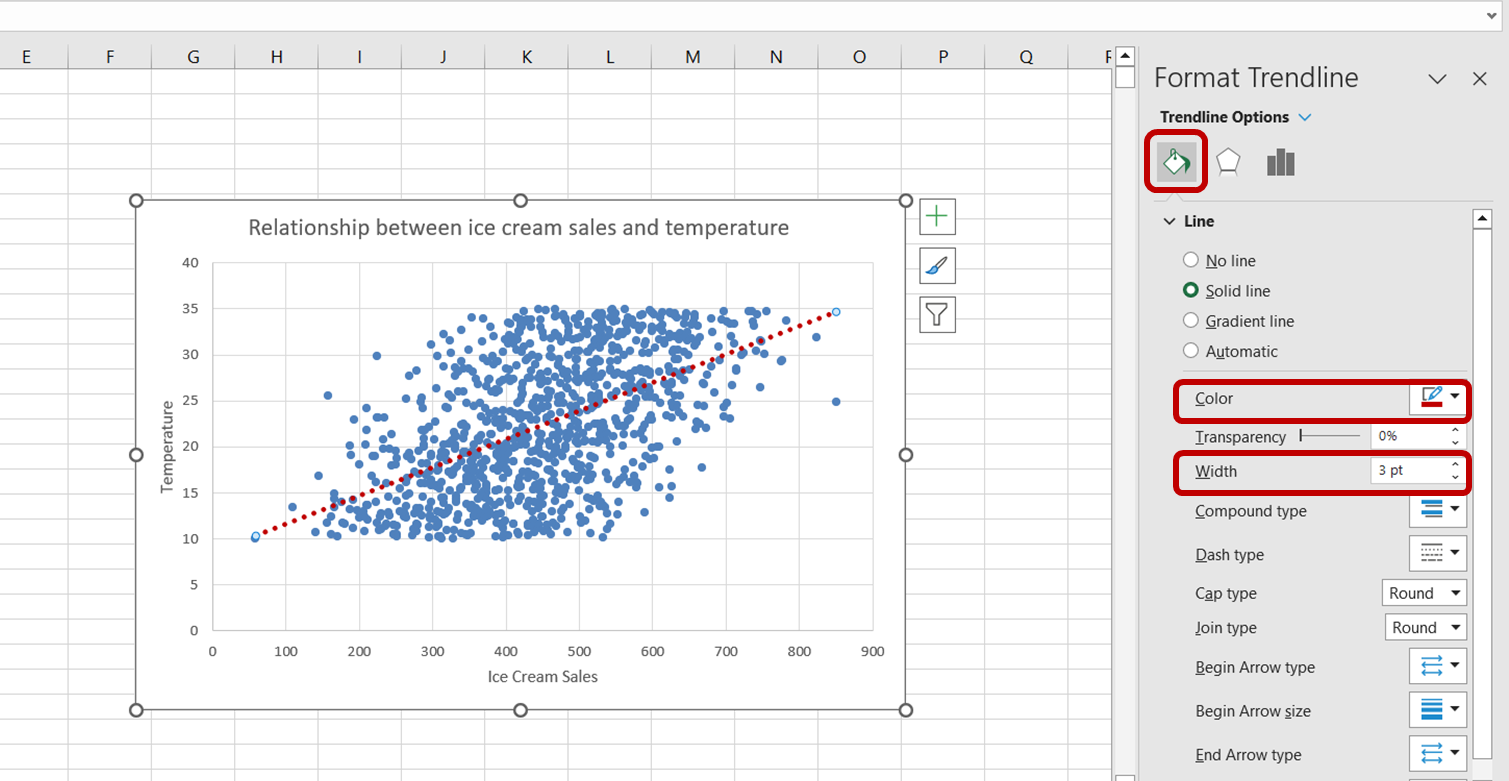
Ahora hemos creado con éxito una visualización para comprender mejor la relación entre las ventas de helados y la temperatura.

Sólo con mirar el gráfico anterior, podemos decir que existe una relación positiva entre la temperatura y las ventas de helados. A medida que aumenta la temperatura, parece que también aumentan las ventas de helados, lo que indica que la temperatura es un predictor significativo de las ventas de helados.

Observa que esta observación es similar a la que derivamos de los resultados del análisis de regresión de la sección anterior.

Reflexiones finales

Ahora ya sabes cómo realizar una regresión lineal en Excel, interpretar diversas medidas estadísticas para evaluar el ajuste de un modelo y visualizar el análisis de regresión mediante gráficos de dispersión y líneas de tendencia.

Pero el viaje no termina aquí.

Lo creas o no, sólo hemos arañado la superficie del modelado predictivo, y hay mucho más que aprender. He aquí algunos posibles pasos siguientes para profundizar en el tema.

Consulta

Practica los conceptos que has aprendido en este artículo para asegurarte de que no los olvidas. Por ejemplo, toma el conjunto de datos utilizado en este tutorial y crea un gráfico de dispersión para ilustrar la relación entre las ventas y los precios de los helados.

Incluso puedes dar un paso más aprendiendo a mostrar la ecuación de regresión en la línea de tendencia.

Dominio de Excel

Como hemos establecido anteriormente en este artículo, el amplio uso de Excel en numerosas organizaciones lo sitúa en un lugar muy demandado. Tener un buen dominio de Excel puede mejorar significativamente tus posibilidades de empleo en diversos sectores, debido a su amplia aplicación.

Si has encontrado dificultades al seguir este tutorial, o si aún no te sientes cómodo con las fórmulas de Excel, considera la posibilidad de inscribirte en nuestro curso de aprendizaje de Fundamentos de Excel. Este curso te introducirá en diversas técnicas de visualización de datos, tablas dinámicas y funciones lógicas como los CONTADORES y los SI anidados, allanando el camino hacia el dominio de Excel.