Um guia abrangente para usar a ANOVA no Excel

A análise estatística é fundamental para a tomada de decisões baseadas em dados em vários campos, incluindo negócios, saúde, educação e pesquisa científica. Um método estatístico comumente usado em ambientes acadêmicos e comerciais é a Análise de Variância, ou ANOVA.

O Microsoft Excel oferece uma plataforma avançada e fácil de usar para a realização de ANOVA. Sua interface intuitiva beneficia os iniciantes, eliminando a necessidade de software estatístico especializado, como o SPSS ou o SAS.

Este guia simplificará o processo de realização de ANOVA no Excel, fornecendo instruções claras e passo a passo para ajudar você a realizar e interpretar testes ANOVA com confiança. Seja você um estudante, um pesquisador ou um profissional que deseja aprimorar suas habilidades analíticas, este guia o ajudará a aprender como aproveitar o Excel para uma de suas necessidades estatísticas comuns.

O que é ANOVA?

ANOVA é um método estatístico usado para determinar se há diferenças significativas entre as médias de três ou mais grupos independentes. Eles são semelhantes a outro teste estatístico chamado teste t, que é usado para determinar se há uma diferença significativa entre as médias de dois grupos. A ANOVA e os testes t representam duas das muitas técnicas estatísticas abordadas em nosso curso abrangente de Análise de dados no Excel, que vale a pena visitar se você quer mesmo se tornar proficiente em estatística.

A ANOVA funciona comparando a variação dentro de cada grupo com a variação entre os grupos para avaliar se as médias dos grupos são iguais. Se a variação entre grupos for significativamente maior do que a variação dentro do grupo, isso sugere que pelo menos uma média de grupo difere das outras.

Em termos gerais, há dois tipos de ANOVA:

• ANOVA de uma via: Uma ANOVA unidirecional examina o efeito de uma única variável independente em uma variável dependente, comparando as médias de três ou mais grupos.
• ANOVA de duas vias: Uma ANOVA de duas vias avalia o impacto de duas variáveis independentes simultaneamente e examina sua interação. 

Os pesquisadores acadêmicos usam esses testes para analisar os resultados após a realização de um estudo controlado. Por exemplo, os pesquisadores podem usar a ANOVA para comparar a eficácia de diferentes tratamentos ou medicamentos em vários grupos de pacientes. As empresas com fins lucrativos podem usar a ANOVA para tomar decisões baseadas em dados, como a comparação dos índices de satisfação do cliente entre vários centros de atendimento ou o desempenho de campanhas publicitárias.

Por que o Microsoft Excel é bom para ANOVA

Aqui estão as etapas ordenadas necessárias para você executar a ANOVA manualmente. Para referência, a proporção f é a estatística de teste usada na ANOVA para determinar se há diferenças significativas entre as médias dos grupos. Isso envolve vários cálculos para chegar à estatística. 

1. Calcule a média geral: Encontre a média de todos os pontos de dados combinados.
2. Calcule as médias do grupo: Determine a média de cada grupo individual.
3. Calcule a soma total de quadrados: Meça a variação total nos dados somando as diferenças quadráticas entre cada ponto de dados e a média geral.
4. Calcule a soma de quadrados entre grupos: Meça a variação entre as médias do grupo e a média geral.
5. Calcule a soma de quadrados dentro dos grupos: Meça a variação dentro de cada grupo somando as diferenças quadráticas entre cada ponto de dados e a média de seu grupo.
6. Calcule o quadrado médio entre grupos: Divida a soma dos quadrados entre os grupos pelos graus de liberdade entre os grupos.
7. Calcule o quadrado médio dentro dos grupos: Divida a soma de quadrados dentro dos grupos pelos graus de liberdade dentro dos grupos, em que os graus de liberdade dentro dos grupos são o número total de observações menos o número de grupos.
8. Calcule o índice F: Divida o quadrado médio entre os grupos pelo quadrado médio dentro dos grupos para determinar o índice f.

Como você pode ver, o cálculo manual da ANOVA é um pouco complicado. Por esse motivo, o software é o caminho a ser seguido, e o Microsoft Excel se destaca devido ao seu amplo uso na maioria das empresas e ambientes acadêmicos. 

Lembre-se também de que, de modo geral, os cálculos da ANOVA fazem parte de projetos analíticos maiores. Além do poder estatístico do Excel, a disponibilidade de outros recursos, como as belas visualizações no Excel, reforça o argumento de que o Microsoft Excel é uma ótima ferramenta para ANOVA. 

Como habilitar o Data Analysis ToolPak no Excel

Os suplementos do Excel são programas ou recursos suplementares que podem ser instalados e integrados ao Excel para aprimorar sua funcionalidade. O Data Analysis ToolPak é um desses add-ins que ajuda você a atender à maioria dos requisitos de análise de dados.

O suplemento Data Analysis ToolPak não é ativado por padrão; portanto, você terá que verificar se consegue localizar o ícone Data Analysis no canto superior direito da guia Data, conforme mostrado abaixo.

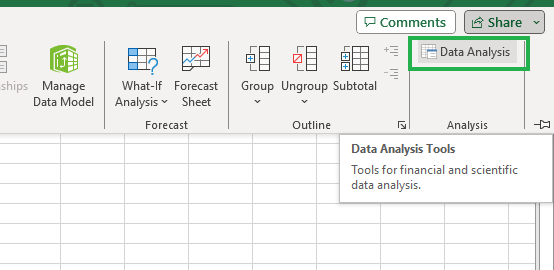
Conjunto de ferramentas de análise de dados no Excel

Se você não vir o Data Analysis ToolPak, isso pode significar que ele não está ativado. Para ativá-la, clique em File (Arquivo ) no menu e selecione Options (Opções).

Selecionando opções da Selecionando opções da guia File

Quando a caixa de diálogo Opções do Excel for aberta, selecione Suplementos.

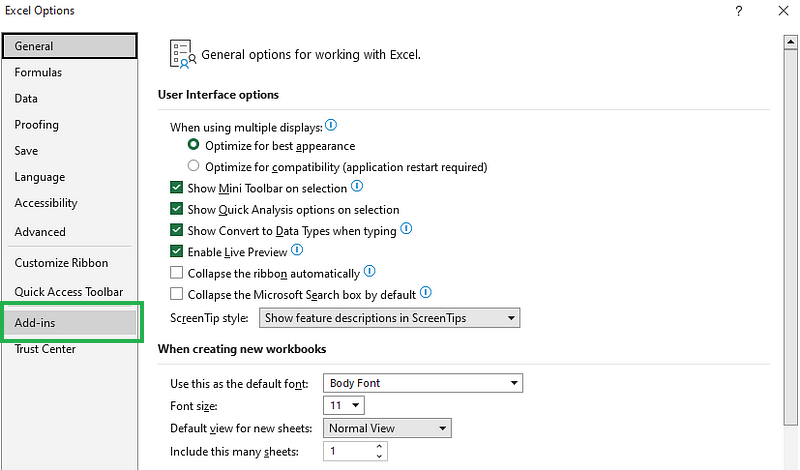Selecione Selecione Add-ins na caixa de diálogo Opções do Excel

Em seguida, na caixa Gerenciar na parte inferior, selecione Suplementos do Excel e clique em Ir.

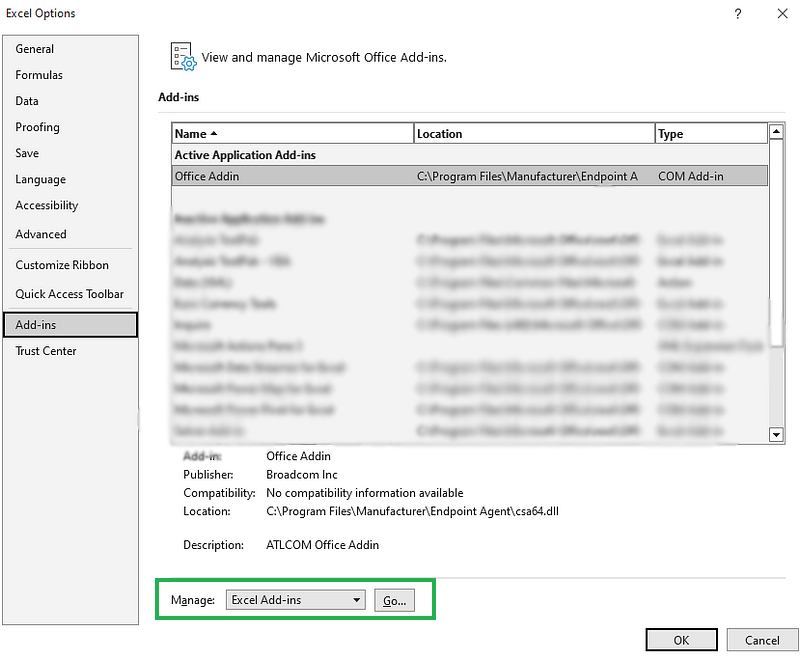Gerenciando os Gerenciando os suplementos do Excel

Na caixa Add-Ins, marque Data Analysis ToolPak e clique em OK.

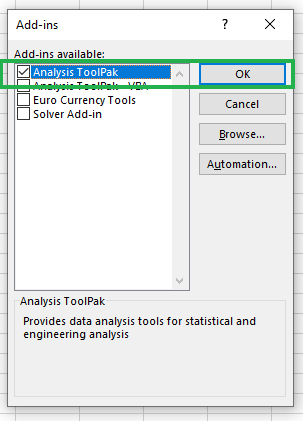
Enabling Data Analysis ToolPak

Agora, quando você verificar novamente a guia Dados, verá o novo ícone Análise de dados. Agora estamos prontos para implementar a ANOVA no Excel usando alguns exemplos.

ANOVA de uma via no Excel: Um exemplo prático

Imagine que você é um analista de dados em uma agência de marketing encarregado de analisar o desempenho de três estratégias de marketing (A, B e C) na receita de vendas.

Sua empresa deseja determinar se há uma diferença significativa na receita média de vendas gerada por essas estratégias. Você também coletou dados de receita de vendas de cinco empresas diferentes de escala semelhante na Região A, onde cada estratégia foi implementada.

Os dados coletados foram tabulados na tabela abaixo:

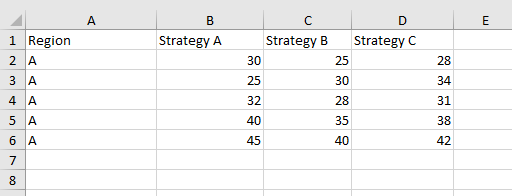
Dados para ANOVA de uma via

Vamos agora usar a ANOVA para ver se há uma diferença significativa entre as vendas médias de cada estratégia.

Como primeira etapa, selecione as colunas B, C e D, incluindo a primeira linha, conforme mostrado abaixo, e clique no ícone Análise de dados para abrir o suplemento Data Analysis Toolpak.

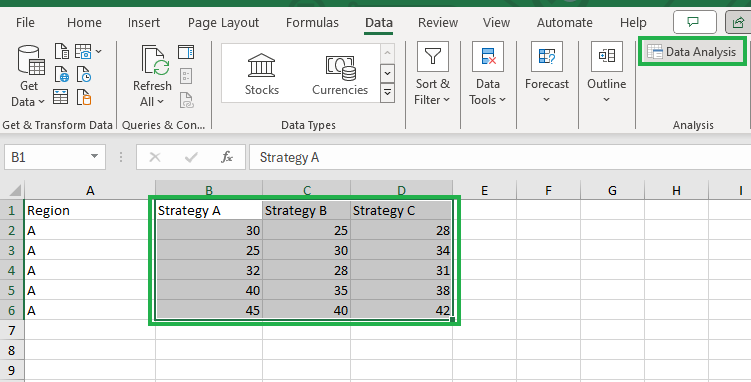Invocando o suplemento Invocando o suplemento Data Analysis Toolpak

Em seguida, selecione Anova: Single Factor na caixa de diálogo e clique em OK.

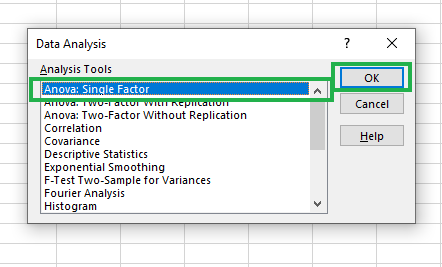
Selecionando Anova: Opção de fator único

Você será solicitado a abrir uma caixa de diálogo, conforme mostrado abaixo.

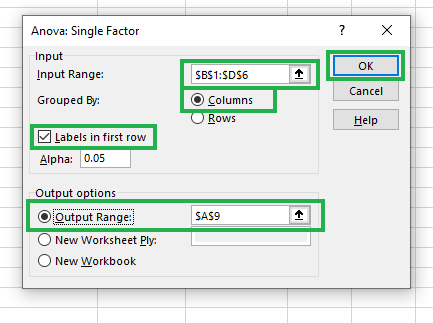
Detalhes de preenchimento para Anova: Fator único

O intervalo de entrada está pré-preenchido, pois já o selecionamos antes de chamar o add-in. Selecione Columns (Colunas ) para a opção Grouped By (Agrupado por ), marque a caixa Labels (Rótulos) na primeira linha e deixe os valores padrão como estão. Para o intervalo de saída, selecionamos uma célula na mesma planilha, por exemplo, $A$9, ou uma nova planilha, como você desejar.

Clique em OK e você verá os resultados calculados na mesma planilha do Excel.

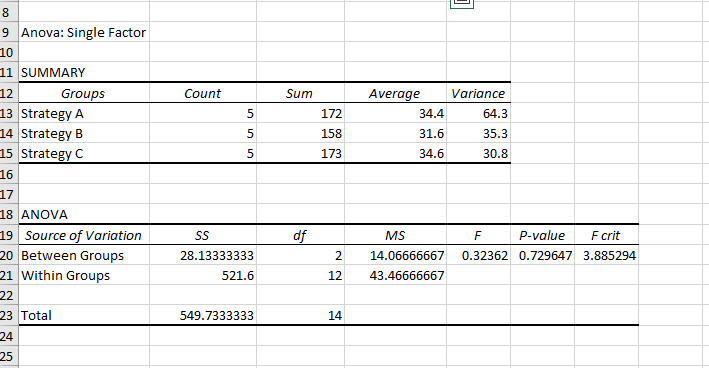Resultados da ANOVA de uma via

Você executou com sucesso uma ANOVA unidirecional em seu conjunto de dados em pouco tempo!

Teste de hipóteses e ANOVA

Para entender melhor os resultados, precisamos nos aprofundar no teste de hipóteses e sua conexão com a ANOVA. O teste de hipóteses é abordado em detalhes em nosso curso de Introdução à Estatística.

No teste de hipótese estatística, a hipótese nula (H0) é uma declaração geral que afirma que não há relação entre dois fenômenos medidos. Você não vê nenhum efeito ou diferença. A hipótese alternativa (H1 ou Ha), por outro lado, sugere que as observações da amostra são influenciadas por alguma causa não aleatória, contradizendo a hipótese nula.

Em nosso exemplo, para um teste ANOVA unidirecional, as hipóteses seriam:

• Hipótese nula (H0): Não há diferença na receita média de vendas gerada pelas três estratégias.
• Hipótese alternativa (Ha): Pelo menos uma estratégia tem uma receita média de vendas diferente.

O objetivo do teste ANOVA é testar essas hipóteses. Se o valor p for menor que o nível de significância (geralmente 0,05), rejeitamos a hipótese nula em favor da hipótese alternativa.

Interpretação dos resultados da ANOVA unidirecional

Ao ler a tabela ANOVA, você verá três linhas de resultados:

• Entre grupos: Essa linha representa a variação entre as diferentes estratégias de marketing e seus cálculos relacionados.
• Dentro dos grupos: Essa linha representa a variação dentro de cada estratégia de marketing e seus cálculos relacionados.
• Total: Essa linha representa a variação total nos dados e os resultados relacionados.

O valor de P é 0,73. Como isso é maior do que o nível de significância típico de 0,05, não conseguimos rejeitar a hipótese nula. Em outras palavras, não há evidências suficientes para afirmar que há uma diferença significativa entre as médias das três estratégias de marketing.

O valor do critério F é 3,88. Sabemos que se a estatística f (0,32) fosse maior que o valor crítico f, teríamos rejeitado a hipótese nula e concluído que há uma diferença significativa entre as médias.

Com base em nosso teste ANOVA, parece que as três estratégias de marketing não diferem significativamente em sua eficácia. Entretanto, é importante lembrar que o fato de você não rejeitar a hipótese nula não prova que a hipótese nula seja verdadeira. Isso significa apenas que não temos evidências fortes o suficiente para concluir o contrário.

Vamos agora descobrir como testar dois fatores e sua influência na variável dependente.

ANOVA de duas vias no Excel: Um exemplo prático

Vamos estender nosso exemplo anterior para incluir um segundo fator. Desta vez, sua empresa quer saber se há alguma diferença significativa na receita gerada com estratégias diferentes e também se há um efeito de interação entre as estratégias e as regiões.

Os dados adicionais coletados foram adicionados à planilha, conforme mostrado abaixo:

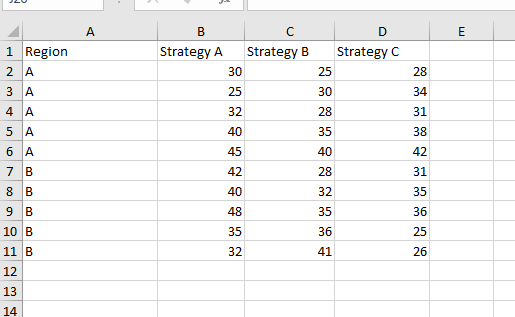
Dados para ANOVA de duas vias

Como agora há dois fatores - estratégia e região - você sabe que precisamos de uma ANOVA de duas vias em vez de uma ANOVA de uma via.

Vamos selecionar todo o intervalo de células e clicar no ícone Análise de dados para chamar o suplemento.

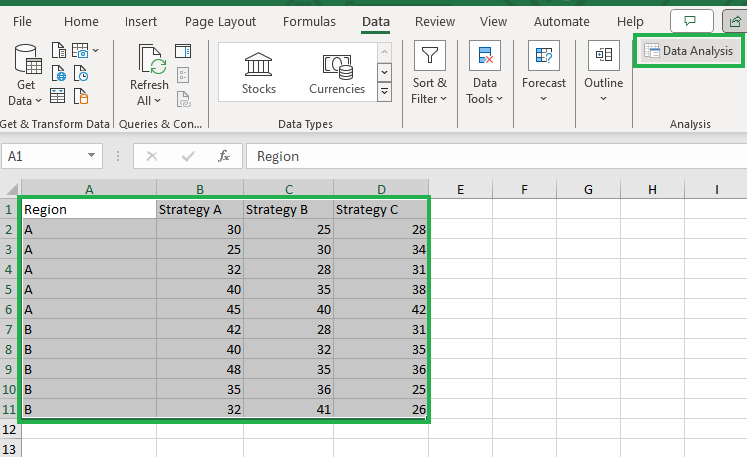Invocando o suplemento Invocando o suplemento Data Analysis Toolpak

Você verá uma caixa de diálogo com duas opções diferentes para ANOVA de duas vias.

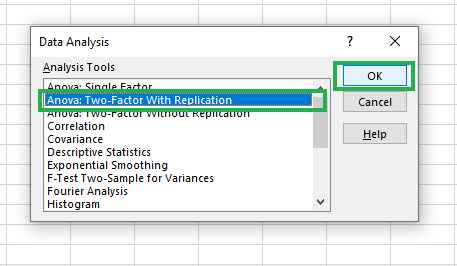
Selecionando Anova: Opção de dois fatores com replicação

• ANOVA: Dois fatores com replicação: Isso é usado quando temos várias observações, ou replicações, para cada combinação de nossos fatores.
• ANOVA: Dois fatores sem replicação: Isso é usado quando temos apenas uma observação para cada combinação de nossos fatores.

Em nosso caso, como temos várias observações para cada combinação de estratégia de marketing (A, B, C) e região (A, B), escolhemos uma ANOVA de dois fatores com replicação.

Depois de clicar em OK, você verá a caixa de diálogo abaixo com um intervalo de entrada pré-preenchido.

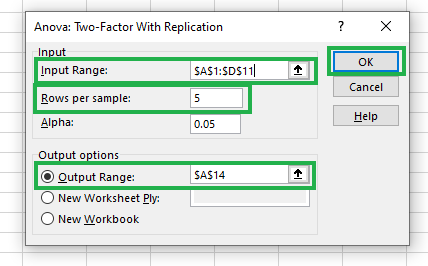
Detalhes de preenchimento para Anova: Dois fatores com replicação

Na opção Rows per sample (Linhas por amostra ), inserimos 5 porque temos cinco pontos de dados para cada uma das regiões. Para o intervalo de saída, podemos selecionar qualquer célula, como $A$14, ou uma nova planilha, como você desejar. 

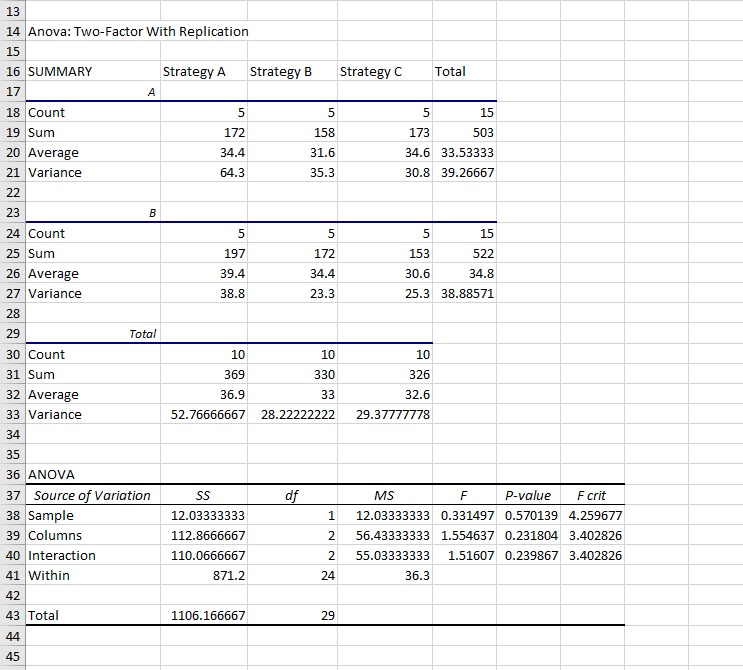Resultados da Resultados da ANOVA de duas vias

É isso aí! Você executou o Two-way ANOVA para o conjunto de dados fornecido em algumas etapas.

Interpretação dos resultados da ANOVA de duas vias

Vamos parar um pouco para você entender como ler a tabela ANOVA e identificar qual linha representa cada fator testado.

• Amostra: A linha Sample representa a variação entre as duas regiões.

• Colunas: A linha Columns representa a variação entre as diferentes estratégias de marketing.

• Interação: A linha Interaction representa o efeito de interação entre as estratégias de marketing e as regiões.

• Dentro de você: A linha Within representa a variação dentro de cada combinação de estratégia de marketing e região.

• Total: A linha Total representa a variação total nos dados.

Se a estatística F for suficientemente grande, o valor p será suficientemente pequeno. Isso nos levará a rejeitar a hipótese nula e a concluir que há diferenças significativas entre as médias dos grupos.

No entanto, em nosso caso, as estatísticas f para a amostra, colunas e interação são menores do que o valor crítico f para cada uma delas, e os valores p são todos maiores do que 0,05. Portanto, não conseguimos rejeitar a hipótese nula em todos os três casos.

Isso significa que não há evidências suficientes para afirmar que há diferenças significativas entre as médias das regiões, as estratégias de marketing ou um efeito de interação entre as estratégias e as regiões.

Conclusão

A ANOVA é uma ferramenta estatística importante em ambientes acadêmicos e comerciais. Este tutorial apresentou a técnica e seus dois tipos principais. Pegamos um exemplo do mundo real e implementamos a ANOVA unidirecional e a ANOVA bidirecional usando o Microsoft Excel.

Além da implementação, também aprendemos a formar uma hipótese e a interpretar os resultados para aceitar ou rejeitar a hipótese.

Para que você domine o Excel para tarefas analíticas semelhantes, o programa Excel Fundamentals seria uma boa aposta, juntamente com a folha de dicas do Excel para referências rápidas.

Feliz aprendizado!