Introducción a t-SNE

En este tutorial, nos adentraremos en el funcionamiento de t-SNE, una potente técnica de reducción de la dimensionalidad y visualización de datos. Lo compararemos con otra técnica popular, PCA, y demostraremos cómo realizar tanto t-SNE como PCA utilizando scikit-learn y plotly express en conjuntos de datos sintéticos y del mundo real.

¿Qué es t-SNE?

t-SNE (t-distributed Stochastic Neighbor Embedding) es una técnica no supervisada de reducción no lineal de la dimensionalidad para la exploración de datos y la visualización de datos de alta dimensión. La reducción no lineal de la dimensionalidad significa que el algoritmo permite separar datos que no pueden separarse mediante una línea recta. 

t-SNE le da una idea e intuición de cómo se organizan los datos en dimensiones superiores. Suele utilizarse para visualizar conjuntos de datos complejos en dos y tres dimensiones, lo que nos permite comprender mejor los patrones y relaciones subyacentes en los datos.

Realice nuestro curso Reducción de la dimensionalidad en Python para aprender a explorar datos de alta dimensión, selección de características y extracción de características.

t-SNE frente a PCA

Tanto t-SNE como PCA son técnicas de reducción dimensional que tienen mecanismos diferentes y funcionan mejor con distintos tipos de datos.

El PCA (Análisis de Componentes Principales) es una técnica lineal que funciona mejor con datos que tienen una estructura lineal. Trata de identificar los componentes principales subyacentes en los datos proyectándolos en dimensiones inferiores, minimizando la varianza y preservando las grandes distancias entre pares. Lea nuestro tutorial sobre Análisis de Componentes Principales (PCA ) para comprender el funcionamiento interno de los algoritmos con ejemplos en R. 

Sin embargo, t-SNE es una técnica no lineal que se centra en preservar las similitudes entre pares de puntos de datos en un espacio de dimensiones inferiores. t-SNE se ocupa de preservar las pequeñas distancias entre pares, mientras que PCA se centra en mantener las grandes distancias entre pares para maximizar la varianza.

En resumen, PCA preserva la varianza de los datos, mientras que t-SNE preserva las relaciones entre los puntos de datos en un espacio de menor dimensión, lo que lo convierte en un algoritmo bastante bueno para visualizar datos complejos de alta dimensión. 

Cómo funciona t-SNE

El algoritmo t-SNE encuentra la medida de similitud entre pares de instancias en un espacio de mayor y menor dimensión. Después, intenta optimizar dos medidas de similitud. Todo ello en tres pasos. 

1. t-SNE modela un punto que se selecciona como vecino de otro punto tanto en dimensiones superiores como inferiores. Comienza calculando una similitud por pares entre todos los puntos de datos en el espacio de alta dimensión utilizando un kernel gaussiano. Los puntos alejados tienen menos probabilidades de ser elegidos que los puntos cercanos. 
2. A continuación, el algoritmo intenta mapear puntos de datos de mayor dimensión en un espacio de menor dimensión preservando las similitudes entre pares. 
3. Se consigue minimizando la divergencia entre la distribución de probabilidad de la alta dimensión original y la de la dimensión inferior. El algoritmo utiliza el descenso de gradiente para minimizar la divergencia. La incrustación de menor dimensión se optimiza hasta alcanzar un estado estable.

El proceso de optimización permite crear clústeres y subclústeres de puntos de datos similares en el espacio de dimensiones inferiores que se visualizan para comprender la estructura y la relación en los datos de dimensiones superiores. 

Ejemplo de t-SNE en Python

En el ejemplo de Python, generaremos datos de clasificación, realizaremos PCA y t-SNE, y visualizaremos los resultados. Para realizar la reducción de dimensionalidad, utilizaremos Scikit-Learn, y para la visualización, utilizaremos Plotly Express. 

Generación del conjunto de datos de clasificación

Utilizaremos la función make_classification de Scikit-Learn para generar datos sintéticos con 6 características, 1500 muestras y 3 clases. 

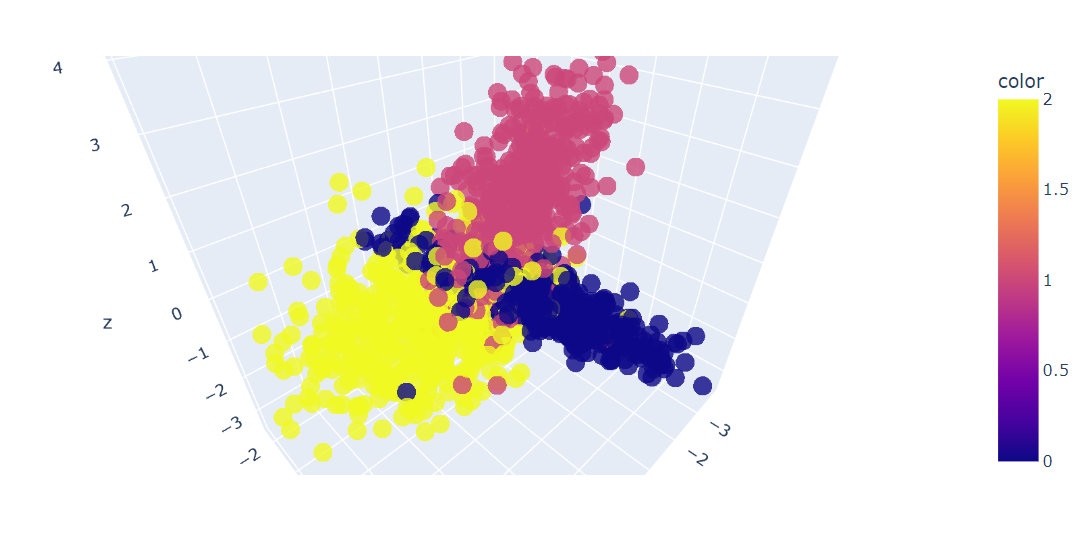
A continuación, trazaremos en 3D las tres primeras características de los datos utilizando la función Plotly Express scatter_3d. 

import plotly.express as px
from sklearn.datasets import make_classification

X, y = make_classification(
    n_features=6,
    n_classes=3,
    n_samples=1500,
    n_informative=2,
    random_state=5,
    n_clusters_per_class=1,
)


fig = px.scatter_3d(x=X[:, 0], y=X[:, 1], z=X[:, 2], color=y, opacity=0.8)
fig.show()

Tenemos un gráfico 3D de los datos; también puede visualizar los datos en un gráfico 2D utilizando la función Plotly Express scatter.

Ajuste y transformación del ACP

Ahora aplicaremos el algoritmo PCA al conjunto de datos para obtener dos componentes PCA. fit_transform aprende y transforma el conjunto de datos al mismo tiempo.  

from sklearn.decomposition import PCA

pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)

Visualización t-SNE Python

Ahora podemos visualizar los resultados mostrando dos componentes PCA en un gráfico de dispersión. 

• x: Primer componente
• y: Segundo acompañante
• color: variable objetivo.

También hemos utilizado la función update_layout para añadir un título y renombrar el eje x y el eje y.

fig = px.scatter(x=X_pca[:, 0], y=X_pca[:, 1], color=y)
fig.update_layout(
    title="PCA visualization of Custom Classification dataset",
    xaxis_title="First Principal Component",
    yaxis_title="Second Principal Component",
)
fig.show()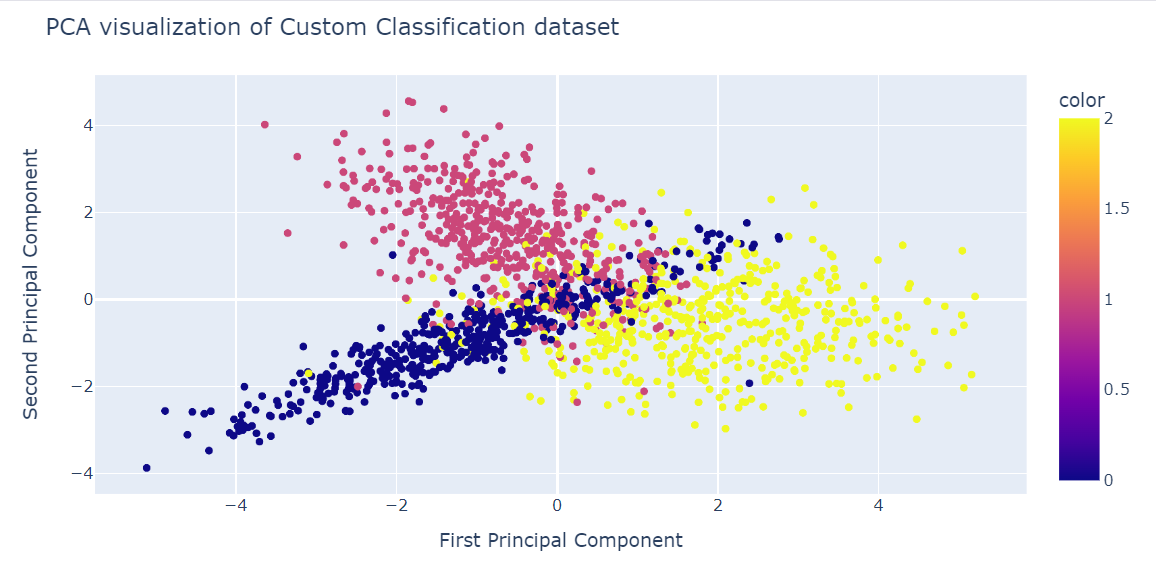

Ajuste y transformación de t-SNE

Ahora aplicaremos el algoritmo t-SNE al conjunto de datos y compararemos los resultados. 

Tras ajustar y transformar los datos, mostraremos la divergencia de Kullback-Leibler (KL) entre la distribución de probabilidad de alta dimensión y la distribución de probabilidad de baja dimensión. 

Una divergencia KL baja es señal de mejores resultados.

from sklearn.manifold import TSNE

tsne = TSNE(n_components=2, random_state=42)
X_tsne = tsne.fit_transform(X)
tsne.kl_divergence_

1.1169137954711914

Visualización t-SNE Python

De forma similar al PCA, visualizaremos dos componentes t-SNE en un gráfico de dispersión. 

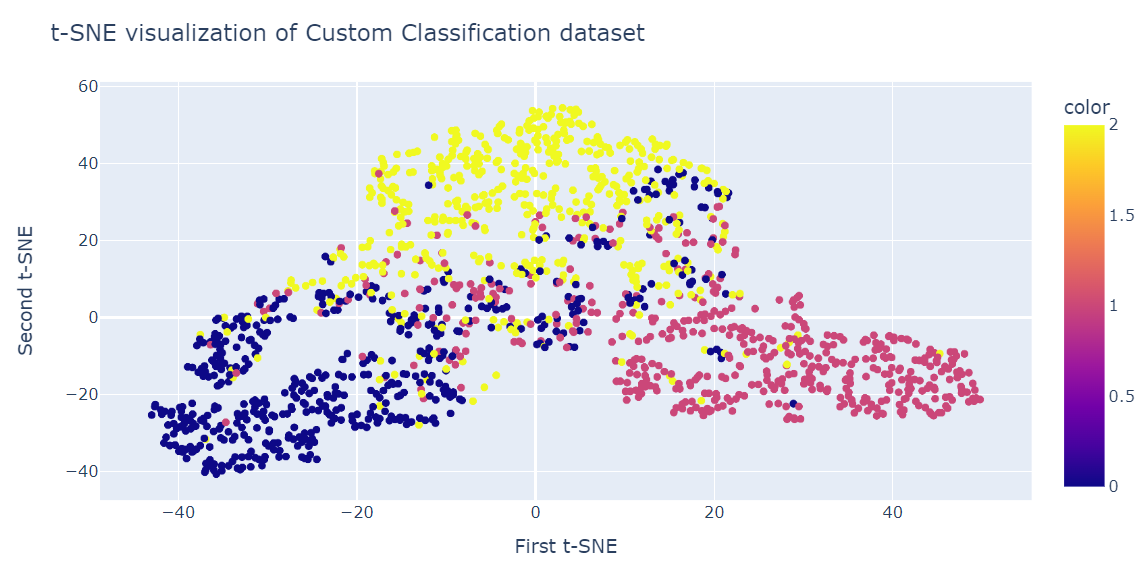
fig = px.scatter(x=X_tsne[:, 0], y=X_tsne[:, 1], color=y)
fig.update_layout(
    title="t-SNE visualization of Custom Classification dataset",
    xaxis_title="First t-SNE",
    yaxis_title="Second t-SNE",
)
fig.show()

El resultado es bastante mejor que el PCA. Podemos ver claramente tres grandes grupos. 

t-SNE en un conjunto de datos sobre la pérdida de clientes

En esta sección, utilizaremos el conjunto de datos reales de rotación de clientes de una empresa de telecomunicaciones iraní. El conjunto de datos contiene información sobre la actividad de los clientes, como fallos en las llamadas y duración de la suscripción, y una etiqueta de churn.

El churn es el porcentaje de clientes que dejan de utilizar un servicio concreto durante un periodo de tiempo determinado.

Nota: El código fuente y el conjunto de datos de ambos ejemplos están disponibles en este cuaderno de DataLab; si quieres modificar y ejecutar el código, haz una copia y listo.

Importación de datos de rotación de clientes

Cargaremos el conjunto de datos utilizando pandas y mostraremos las tres primeras filas.

import pandas as pd

df = pd.read_csv("data/customer_churn.csv")
df.head(3)

PCA Reducción de la dimensionalidad

Después de eso, lo haremos:

• Crear características (X) y objetivo (y) utilizando la columna Churn.
• Normalice las características utilizando un escalador estándar.
• Divida el conjunto de datos en un conjunto de entrenamiento y otro de pruebas.
• Aplique el PCA al conjunto de datos de entrenamiento.
• Obtener la puntuación utilizando el conjunto de datos de prueba. La puntuación representa la log-verosimilitud media de todas las muestras.

from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

X = df.drop('Churn', axis=1)
y = df['Churn']

scaler = StandardScaler()
X_norm = scaler.fit_transform(X)

X_train, X_test, y_train, y_test = train_test_split(
    X_norm, y, random_state=13, test_size=0.25, shuffle=True
)

pca = PCA(n_components=2)
X_train_pca = pca.fit_transform(X_train)

pca.score(X_test)

-17.04482851288105

Visualización de PCA

Ahora visualizaremos el resultado del PCA utilizando el gráfico de dispersión de Plotly Express. 

fig = px.scatter(x=X_train_pca[:, 0], y=X_train_pca[:, 1], color=y_train)
fig.update_layout(
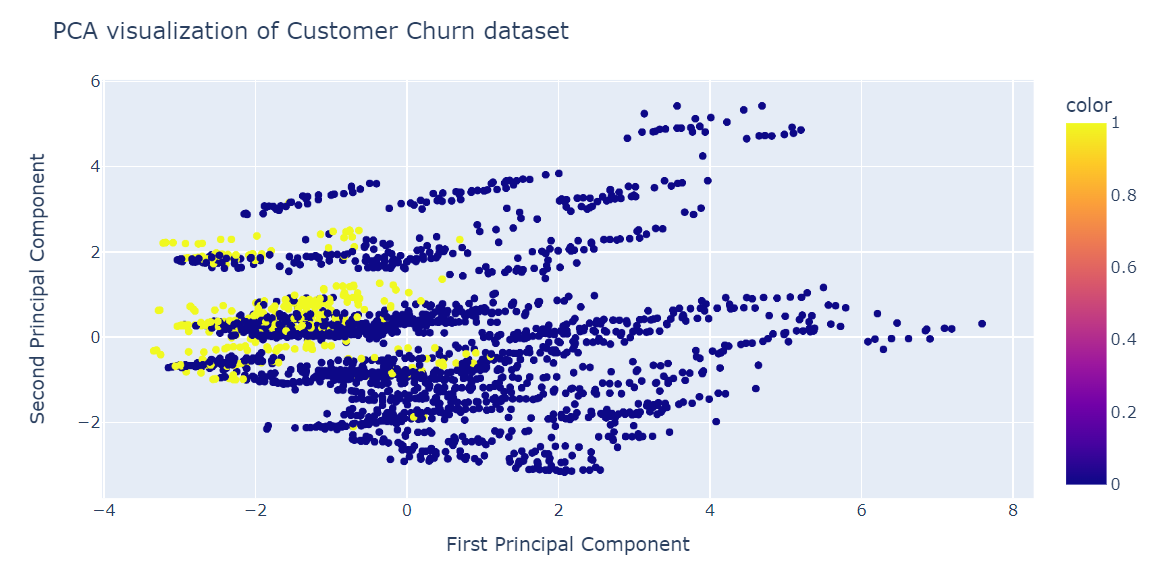
    title="PCA visualization of Customer Churn dataset",
    xaxis_title="First Principal Component",
    yaxis_title="Second Principal Component",
)
fig.show()

El ACP no era bueno para crear conglomerados. Los datos en la dimensión baja parecen aleatorios. También podría significar que las características del conjunto de datos están muy sesgadas o que no tiene una estructura de correlación fuerte. 

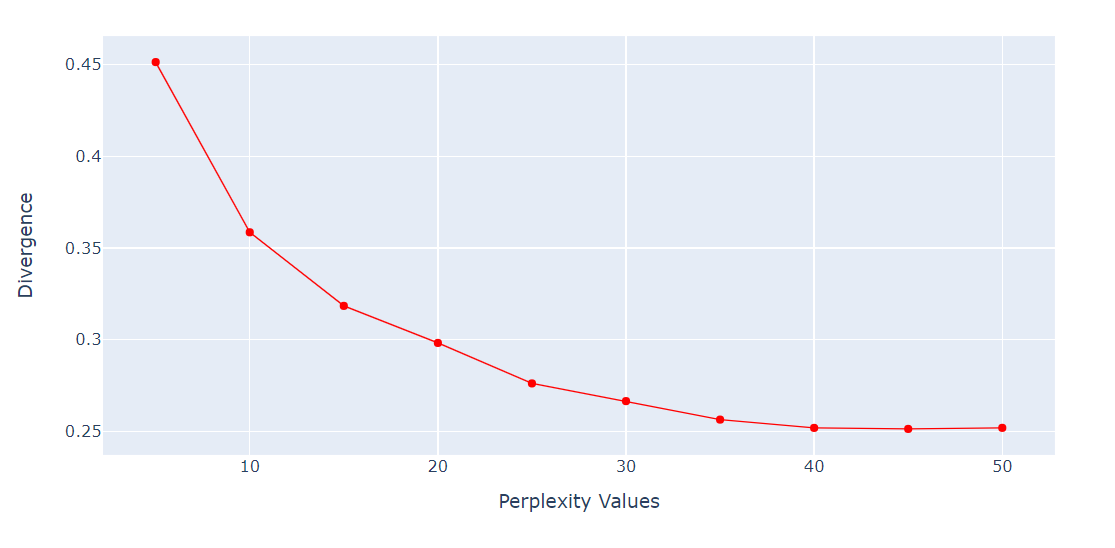
Comprobar Perplejidad vs. Divergencia

Para el algoritmo t-SNE, la perplejidad es un hiperparámetro muy importante. Controla el número efectivo de vecinos que cada punto considera durante el proceso de reducción de la dimensionalidad. 

Ejecutaremos un bucle para obtener la métrica de Divergencia KL en varias perplejidades de 5 a 55 con 5 puntos de diferencia. A continuación, visualizaremos el resultado utilizando el gráfico de líneas de Plotly Express.

import numpy as np

perplexity = np.arange(5, 55, 5)
divergence = []

for i in perplexity:
    model = TSNE(n_components=2, init="pca", perplexity=i)
    reduced = model.fit_transform(X_train)
    divergence.append(model.kl_divergence_)
fig = px.line(x=perplexity, y=divergence, markers=True)
fig.update_layout(xaxis_title="Perplexity Values", yaxis_title="Divergence")
fig.update_traces(line_color="red", line_width=1)
fig.show()

La Divergencia KL se ha vuelto constante después de 40 perplejidades. Por lo tanto, utilizaremos 40 de perplejidad en el algoritmo t-SNE.  

Reducción de la dimensionalidad t-SNE

Ahora ajustaremos t-SNE y transformaremos los datos a dimensiones inferiores utilizando 40 perplejidades para obtener la Divergencia KL más baja. 

from sklearn.manifold import TSNE

tsne = TSNE(n_components=2,perplexity=40, random_state=42)
X_train_tsne = tsne.fit_transform(X_train)

tsne.kl_divergence_

0.258713960647583

Visualización de t-SNE

Ahora vamos a utilizar el gráfico de dispersión Plotly para mostrar los componentes y las clases de destino. 

fig = px.scatter(x=X_train_tsne[:, 0], y=X_train_tsne[:, 1], color=y_train)
fig.update_layout(
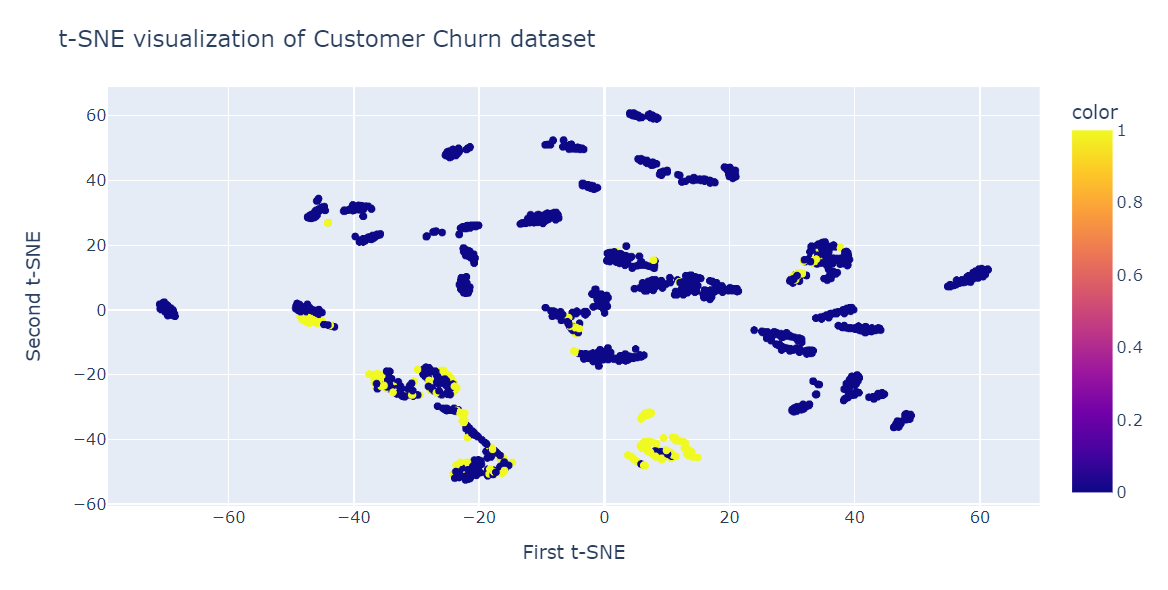
    title="t-SNE visualization of Customer Churn dataset",
    xaxis_title="First t-SNE",
    yaxis_title="Second t-SNE",
)
fig.show()

Como podemos ver, tenemos múltiples clusters y subclusters. Podemos utilizar esta información para comprender el patrón y elaborar una estrategia para retener a los clientes existentes. 

Aplicación de t-SNE

Además de visualizar datos multidimensionales complejos, t-SNE tiene otros usos, sobre todo en el campo de la medicina. 

1. Agrupación y clasificación: para agrupar puntos de datos similares en un espacio de menor dimensión. También puede utilizarse para clasificar y encontrar patrones en los datos. 
2. Detección de anomalías: para identificar valores atípicos y anomalías en los datos. 
3. Procesamiento del lenguaje natural: para visualizar incrustaciones de palabras generadas a partir de un gran corpus de texto que facilita la identificación de similitudes y relaciones entre palabras.
4. Seguridad informática: para visualizar patrones de tráfico de red y detectar anomalías.
5. Investigación del cáncer: para visualizar perfiles moleculares de muestras tumorales e identificar subtipos de cáncer. 
6. Interpretación del dominio geológico: para visualizar atributos sísmicos e identificar anomalías geológicas. 
7. Procesamiento de señales biomédicas: para visualizar electroencefalogramas (EEG) y detectar patrones de actividad cerebral. 

Conclusión

t-SNE es una potente herramienta de visualización para revelar patrones y estructuras ocultos en conjuntos de datos complejos. Puede utilizarlo para imágenes, audio, biológicos y datos individuales para identificar anomalías y patrones. 

En esta entrada del blog, hemos aprendido sobre t-SNE, una popular técnica de reducción de dimensionalidad que puede visualizar datos no lineales de alta dimensión en un espacio de baja dimensión. Hemos explicado la idea principal de t-SNE, cómo funciona y sus aplicaciones. Además, mostramos algunos ejemplos de aplicación de t-SNE a conjuntos de datos sintéticos y reales y cómo interpretar los resultados. 

t-SNE forma parte del aprendizaje no supervisado, y el siguiente paso natural es comprender la agrupación jerárquica, el PCA, la descorrelación y el descubrimiento de características interpretables. Aprenda todos los temas realizando nuestro curso Aprendizaje no supervisado en Python.