Einführung in t-SNE

t-SNE vs PCA

Sowohl t-SNE als auch PCA sind Techniken zur Dimensionsreduktion, die unterschiedliche Mechanismen haben und mit verschiedenen Datentypen am besten funktionieren.

PCA (Principal Component Analysis) ist eine lineare Technik, die am besten mit Daten funktioniert, die eine lineare Struktur haben. Sie versucht, die zugrunde liegenden Hauptkomponenten in den Daten zu identifizieren, indem sie auf niedrigere Dimensionen projiziert, die Varianz minimiert und große paarweise Abstände beibehält. Lies unser Tutorial zur Hauptkomponentenanalyse (PCA), um die Funktionsweise der Algorithmen mit R-Beispielen zu verstehen. 

t-SNE ist eine nichtlineare Technik, die sich darauf konzentriert, die paarweisen Ähnlichkeiten zwischen Datenpunkten in einem niedrigdimensionalen Raum zu erhalten. t-SNE ist darauf ausgerichtet, kleine paarweise Abstände zu erhalten, während PCA sich darauf konzentriert, große paarweise Abstände zu erhalten, um die Varianz zu maximieren.

Zusammenfassend lässt sich sagen, dass die PCA die Varianz in den Daten bewahrt, während t-SNE die Beziehungen zwischen den Datenpunkten in einem niedrigdimensionalen Raum bewahrt, was ihn zu einem recht guten Algorithmus für die Visualisierung komplexer hochdimensionaler Daten macht. 

Wie t-SNE funktioniert

Der t-SNE-Algorithmus findet das Ähnlichkeitsmaß zwischen Paaren von Instanzen im höher- und niederdimensionalen Raum. Danach wird versucht, zwei Ähnlichkeitsmaße zu optimieren. All das geschieht in drei Schritten. 

1. t-SNE modelliert, dass ein Punkt als Nachbar eines anderen Punktes sowohl in höheren als auch in niedrigeren Dimensionen ausgewählt wird. Es beginnt mit der Berechnung einer paarweisen Ähnlichkeit zwischen allen Datenpunkten im hochdimensionalen Raum unter Verwendung eines Gaußschen Kernels. Die Punkte, die weit voneinander entfernt sind, haben eine geringere Wahrscheinlichkeit, ausgewählt zu werden, als die Punkte, die nahe beieinander liegen. 
2. Dann versucht der Algorithmus, höherdimensionale Datenpunkte auf einen niedrigerdimensionalen Raum abzubilden und dabei die paarweisen Ähnlichkeiten zu erhalten. 
3. Dies wird erreicht, indem die Divergenz zwischen der Wahrscheinlichkeitsverteilung des hochdimensionalen Originals und der niedrigeren Dimension minimiert wird. Der Algorithmus nutzt den Gradientenabstieg, um die Divergenz zu minimieren. Die niederdimensionale Einbettung wird auf einen stabilen Zustand optimiert.

Der Optimierungsprozess ermöglicht die Bildung von Clustern und Sub-Clustern ähnlicher Datenpunkte im niederdimensionalen Raum, die visualisiert werden, um die Struktur und Beziehung in den höherdimensionalen Daten zu verstehen. 

t-SNE Python Beispiel

In dem Python-Beispiel werden wir Klassifizierungsdaten erzeugen, PCA und t-SNE durchführen und die Ergebnisse visualisieren. Für die Dimensionalitätsreduktion verwenden wir Scikit-Learn und für die Visualisierung Plotly Express. 

Klassifizierungsdatensatz generieren

Wir werden die Funktion make_classification von Scikit-Learn verwenden, um synthetische Daten mit 6 Merkmalen, 1500 Stichproben und 3 Klassen zu erzeugen. 

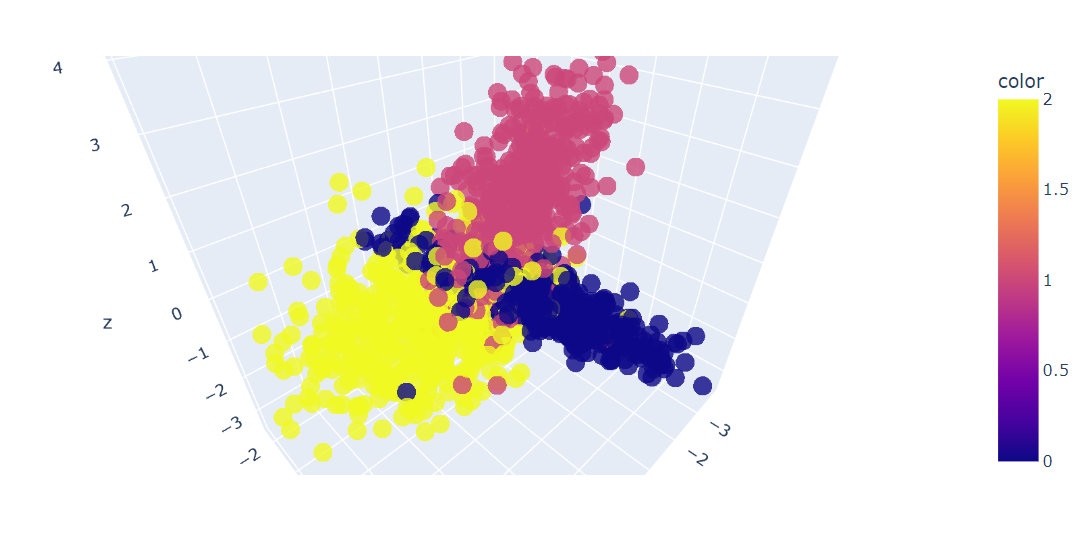
Danach werden wir die ersten drei Merkmale der Daten mit der Funktion Plotly Express scatter_3d in 3D darstellen. 

import plotly.express as px
from sklearn.datasets import make_classification

X, y = make_classification(
    n_features=6,
    n_classes=3,
    n_samples=1500,
    n_informative=2,
    random_state=5,
    n_clusters_per_class=1,
)


fig = px.scatter_3d(x=X[:, 0], y=X[:, 1], z=X[:, 2], color=y, opacity=0.8)
fig.show()

Wir haben eine 3D-Darstellung der Daten; du kannst die Daten auch in einem 2D-Diagramm visualisieren, indem du die Funktion Plotly Express scatter verwendest.

Anpassen und Transformieren der PCA

Wir wenden nun den PCA-Algorithmus auf den Datensatz an, um zwei PCA-Komponenten zu erhalten. Die fit_transform lernt und transformiert den Datensatz gleichzeitig.  

from sklearn.decomposition import PCA

pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)

t-SNE Visualisierung Python

Wir können die Ergebnisse nun visualisieren, indem wir zwei PCA-Komponenten in einem Streudiagramm darstellen. 

• x: Erste Komponente
• y: Zweiter Begleiter
• Farbe: Zielvariable.

Wir haben auch die Funktion update_layout verwendet, um einen Titel hinzuzufügen und die x- und y-Achse umzubenennen.

fig = px.scatter(x=X_pca[:, 0], y=X_pca[:, 1], color=y)
fig.update_layout(
    title="PCA visualization of Custom Classification dataset",
    xaxis_title="First Principal Component",
    yaxis_title="Second Principal Component",
)
fig.show()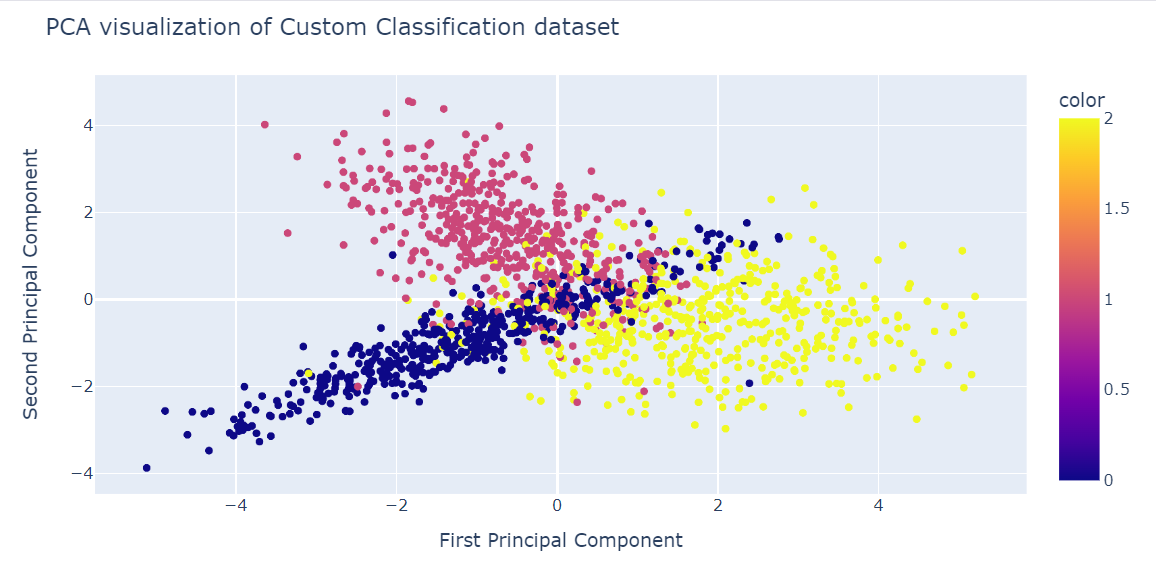

Anpassen und Transformieren von t-SNE

Jetzt werden wir den t-SNE-Algorithmus auf den Datensatz anwenden und die Ergebnisse vergleichen. 

Nach der Anpassung und Umwandlung der Daten zeigen wir die Kullback-Leibler (KL)-Divergenz zwischen der hochdimensionalen Wahrscheinlichkeitsverteilung und der niedrigdimensionalen Wahrscheinlichkeitsverteilung an. 

Eine geringe KL-Divergenz ist ein Zeichen für bessere Ergebnisse.

from sklearn.manifold import TSNE

tsne = TSNE(n_components=2, random_state=42)
X_tsne = tsne.fit_transform(X)
tsne.kl_divergence_

1.1169137954711914

t-SNE Visualisierung Python

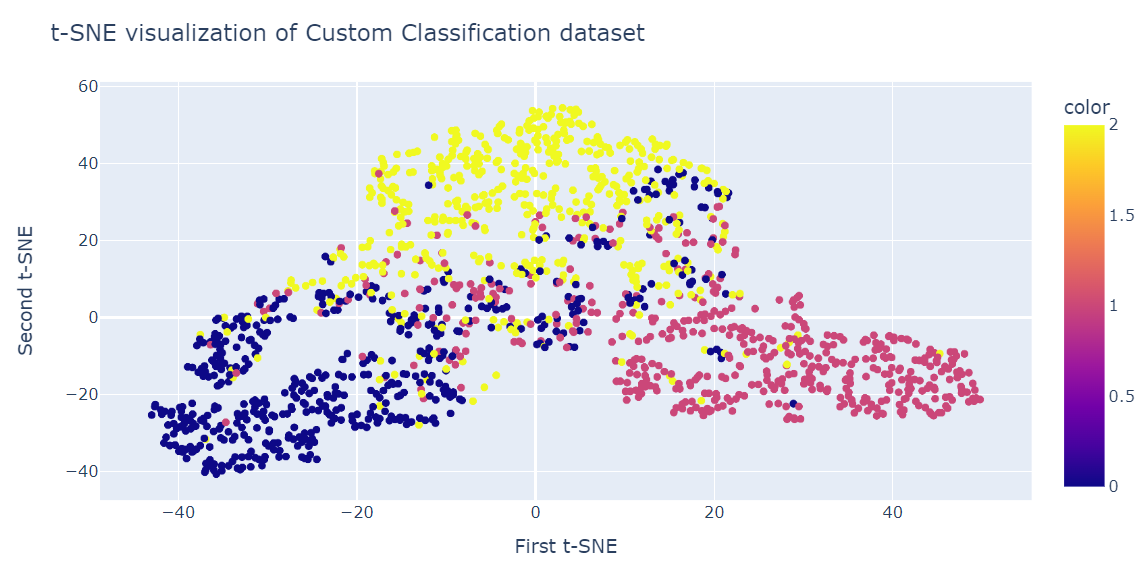
Ähnlich wie bei der PCA werden wir zwei t-SNE-Komponenten in einem Streudiagramm visualisieren. 

fig = px.scatter(x=X_tsne[:, 0], y=X_tsne[:, 1], color=y)
fig.update_layout(
    title="t-SNE visualization of Custom Classification dataset",
    xaxis_title="First t-SNE",
    yaxis_title="Second t-SNE",
)
fig.show()

Das Ergebnis ist deutlich besser als die PCA. Wir können deutlich drei große Cluster erkennen. 

t-SNE auf dem Datensatz zur Kundenabwanderung

In diesem Abschnitt verwenden wir den realen Datensatz zur Kundenabwanderung eines iranischen Telekommunikationsunternehmens. Der Datensatz enthält Informationen über die Aktivität der Kunden, wie z. B. Anrufausfälle und die Länge des Abonnements, sowie ein Churn-Label.

Unter Abwanderung versteht man den Prozentsatz der Kunden, die die Nutzung eines bestimmten Dienstes innerhalb eines bestimmten Zeitraums einstellen.

Hinweis: Der Quellcode und der Datensatz beider Beispiele sind in dieser DataLab-Arbeitsmappe verfügbar. Wenn du den Code optimieren und ausführen möchtest, kopiere ihn einfach und schon kann es losgehen!

Importieren des Datensatzes zur Kundenabwanderung

Wir werden den Datensatz mit Pandas laden und die ersten drei Zeilen anzeigen.

import pandas as pd

df = pd.read_csv("data/customer_churn.csv")
df.head(3)

PCA Dimensionalitätsreduktion

Danach werden wir:

• Erstelle Merkmale (X) und Ziel (y) mit Hilfe der Spalte Churn.
• Normalisiere die Merkmale mit einem Standard-Skalierer.
• Teile den Datensatz in einen Trainings- und einen Testsatz auf.
• Wende die PCA auf den Trainingsdatensatz an.
• Erhalte die Punktzahl aus dem Testdatensatz. Die Punktzahl stellt die durchschnittliche Log-Wahrscheinlichkeit aller Stichproben dar.

from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

X = df.drop('Churn', axis=1)
y = df['Churn']

scaler = StandardScaler()
X_norm = scaler.fit_transform(X)

X_train, X_test, y_train, y_test = train_test_split(
    X_norm, y, random_state=13, test_size=0.25, shuffle=True
)

pca = PCA(n_components=2)
X_train_pca = pca.fit_transform(X_train)

pca.score(X_test)

-17.04482851288105

PCA visualisieren

Wir werden nun das PCA-Ergebnis mit dem Plotly Express Streudiagramm visualisieren. 

fig = px.scatter(x=X_train_pca[:, 0], y=X_train_pca[:, 1], color=y_train)
fig.update_layout(
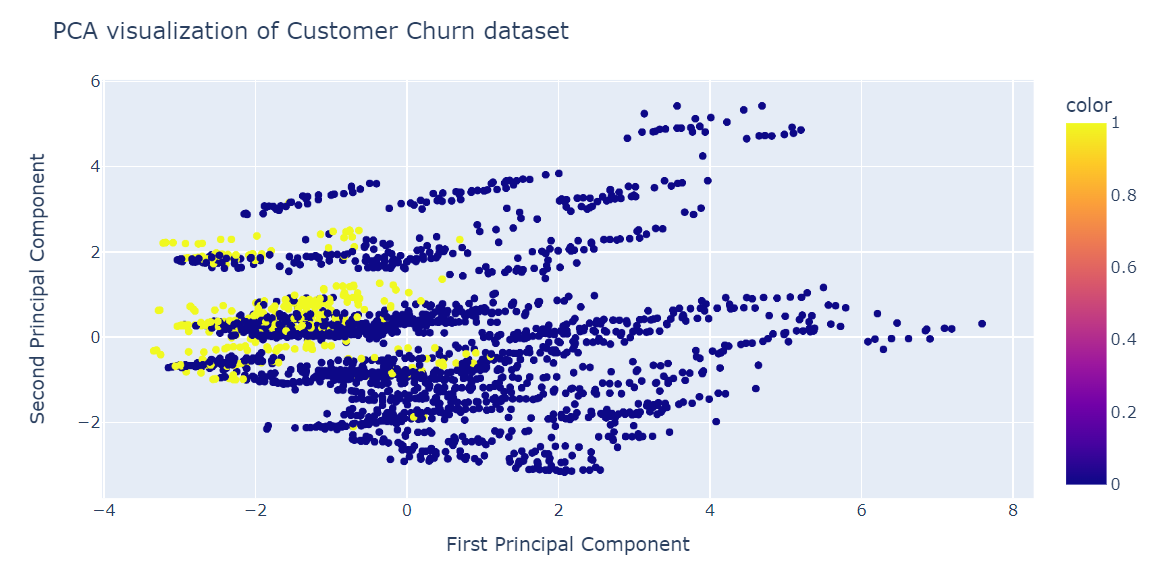
    title="PCA visualization of Customer Churn dataset",
    xaxis_title="First Principal Component",
    yaxis_title="Second Principal Component",
)
fig.show()

Die PCA war nicht gut darin, Cluster zu bilden. Die Daten in der niedrigen Dimension sehen zufällig aus. Es könnte auch bedeuten, dass die Merkmale im Datensatz stark verzerrt sind oder dass er keine starke Korrelationsstruktur aufweist. 

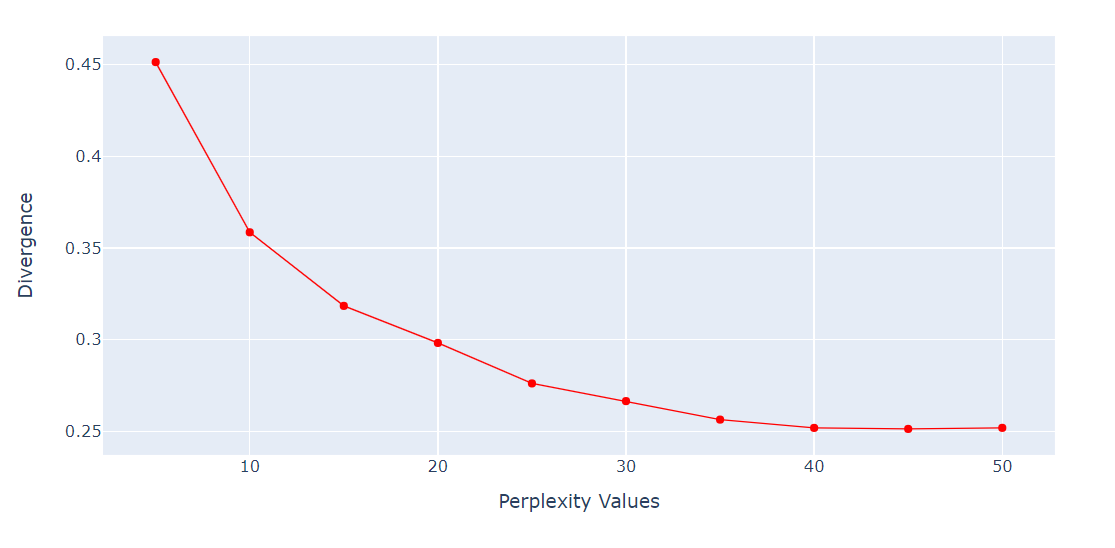
Perplexität vs. Checking Perplexity Divergenz

Für den t-SNE-Algorithmus ist die Komplexität ein sehr wichtiger Hyperparameter. Sie bestimmt die effektive Anzahl der Nachbarn, die jeder Punkt bei der Dimensionalitätsreduktion berücksichtigt. 

Wir werden eine Schleife laufen lassen, um die KL-Divergenz-Metrik für verschiedene Perplexitäten von 5 bis 55 mit 5 Punkten Abstand zu ermitteln. Danach werden wir das Ergebnis mit dem Plotly Express Liniendiagramm anzeigen.

import numpy as np

perplexity = np.arange(5, 55, 5)
divergence = []

for i in perplexity:
    model = TSNE(n_components=2, init="pca", perplexity=i)
    reduced = model.fit_transform(X_train)
    divergence.append(model.kl_divergence_)
fig = px.line(x=perplexity, y=divergence, markers=True)
fig.update_layout(xaxis_title="Perplexity Values", yaxis_title="Divergence")
fig.update_traces(line_color="red", line_width=1)
fig.show()

Die KL-Divergenz ist nach 40 Perplexity konstant geworden. Wir verwenden also 40 Perplexitäten für den t-SNE-Algorithmus.  

t-SNE Dimensionalitätsreduktion

Wir passen nun t-SNE an und transformieren die Daten in niedrigere Dimensionen, indem wir 40 Perplexitäten verwenden, um die niedrigste KL-Divergenz zu erhalten. 

from sklearn.manifold import TSNE

tsne = TSNE(n_components=2,perplexity=40, random_state=42)
X_train_tsne = tsne.fit_transform(X_train)

tsne.kl_divergence_

0.258713960647583

t-SNE visualisieren

Wir werden nun das Plotly Scatter Plot verwenden, um Komponenten und Zielklassen anzuzeigen. 

fig = px.scatter(x=X_train_tsne[:, 0], y=X_train_tsne[:, 1], color=y_train)
fig.update_layout(
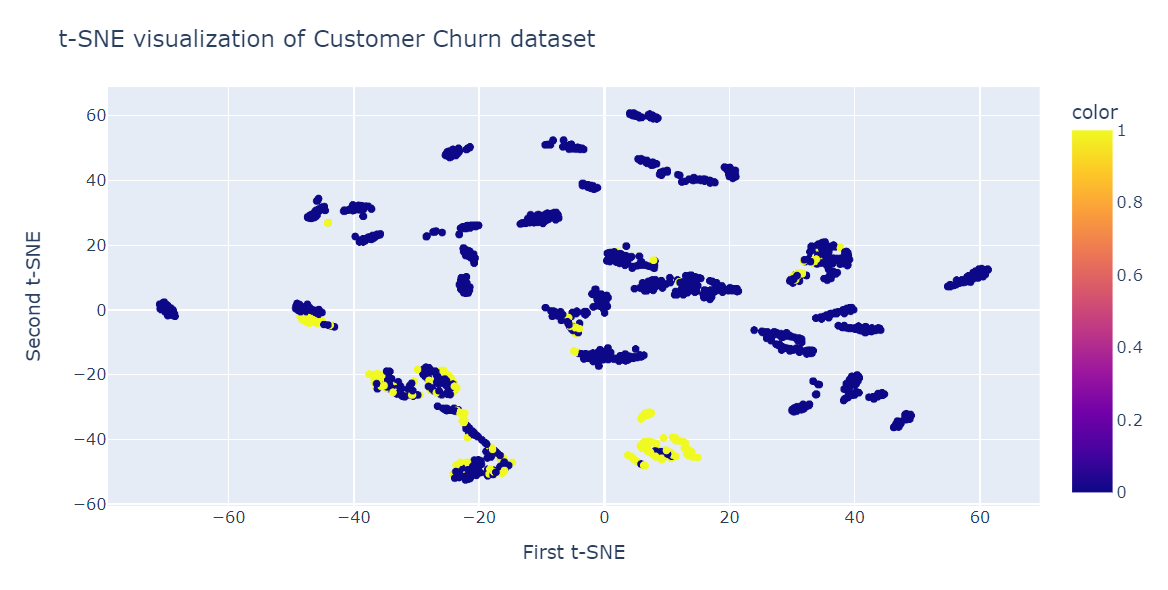
    title="t-SNE visualization of Customer Churn dataset",
    xaxis_title="First t-SNE",
    yaxis_title="Second t-SNE",
)
fig.show()

Wie wir sehen können, gibt es mehrere Cluster und Sub-Cluster. Wir können diese Informationen nutzen, um das Muster zu verstehen und eine Strategie zu entwickeln, um bestehende Kunden zu halten. 

Anwendung von t-SNE

Neben der Visualisierung komplexer mehrdimensionaler Daten wird t-SNE vor allem im medizinischen Bereich eingesetzt. 

1. Clustering und Klassifizierung: Um ähnliche Datenpunkte im niedrigdimensionalen Raum zusammenzufassen. Sie kann auch zur Klassifizierung und zum Auffinden von Mustern in den Daten verwendet werden. 
2. Anomalieerkennung: um Ausreißer und Anomalien in den Daten zu identifizieren. 
3. Verarbeitung natürlicher Sprache: Visualisierung von Worteinbettungen, die aus einem großen Textkorpus generiert wurden, was es einfacher macht, Ähnlichkeiten und Beziehungen zwischen Wörtern zu erkennen.
4. Computersicherheit: zur Visualisierung von Netzwerkverkehrsmustern und zur Erkennung von Anomalien.
5. Krebsforschung: um molekulare Profile von Tumorproben zu visualisieren und Subtypen von Krebs zu identifizieren. 
6. Geologische Interpretation: zur Visualisierung von seismischen Attributen und zur Identifizierung geologischer Anomalien. 
7. Biomedizinische Signalverarbeitung: um das Elektroenzephalogramm (EEG) zu visualisieren und Muster der Gehirnaktivität zu erkennen. 

Fazit

t-SNE ist ein leistungsstarkes Visualisierungswerkzeug, um verborgene Muster und Strukturen in komplexen Datensätzen aufzudecken. Du kannst es für Bilder, Audiodaten, biologische Daten und einzelne Daten verwenden, um Anomalien und Muster zu erkennen. 

In diesem Blogbeitrag haben wir t-SNE kennengelernt, ein beliebtes Verfahren zur Dimensionalitätsreduktion, mit dem hochdimensionale nichtlineare Daten in einem niedrigdimensionalen Raum visualisiert werden können. Wir haben die Grundidee hinter t-SNE, seine Funktionsweise und seine Anwendungen erklärt. Außerdem haben wir einige Beispiele für die Anwendung von t-SNE auf synthetische und reale Datensätze gezeigt und wie die Ergebnisse zu interpretieren sind. 

t-SNE ist ein Teil des unüberwachten Lernens, und der nächste natürliche Schritt ist das Verstehen von hierarchischem Clustering, PCA, Dekorrelation und die Entdeckung von interpretierbaren Merkmalen. Lerne alle Themen in unserem Kurs "Unüberwachtes Lernen in Python ".